MATLAB中的非线性规划

目录

前言

一、非线性规划定义

二、应用范围

三、思路分析

模型建立

初始值设定

约束条件处理

算法选择

参数调整与优化：

四、典型案例

1.代码举例

详细解释：

2.路径优化（以避障问题为例）

3.利润问题

五、注意

总结

---

---

前言

非线性规划作为一门新兴学科，起始于20世纪50年代。1951年，H.W.库恩和A.W.塔克发表的论文中关于最优性条件的论述（后称库恩-塔克条件），是非线性规划正式诞生的标志。随着计算机技术的快速发展，非线性规划在算法和实际应用上取得了显著进步。

*内容有误之处，敬请评论或者联系修改

一、非线性规划定义

非线性规划是指求解目标函数或约束条件中有一个或几个非线性函数的最优化问题的方法。它是运筹学的一个重要分支，广泛应用于工业、交通运输、经济管理和军事等多个领域。

二、应用范围

• 投资组合优化
• 工程设计优化
• 资源分配
• 广告预算优化
• 供应链管理
• 曲线拟合与数据分析
• 环境科学与可持续发展

三、思路分析

模型建立

初始值设定

• 为变量设定合理的初始值（x0），这有助于算法更快地收敛到最优解。
• 不恰当的初始值可能导致算法陷入局部最优或无法收敛。

约束条件处理

• 准确区分并设定线性约束（A, b, Aeq, beq）和非线性约束（nonlcon）。
• 确保所有约束都被正确实现，以避免违反实际问题的限制。

算法选择

• 根据问题的性质和规模选择合适的优化算法，如内点法、序列二次规划法等。
• 了解所选算法的原理和适用性，以便调整参数提高求解效率。

参数调整与优化：

• 根据实际情况调整优化选项（options），如迭代次数、收敛精度等。
• 监控求解过程，根据需要调整参数以改善求解效果。

四、典型案例

1.代码举例

clc,clear
% 主程序
x0 = [0.5, 0.5]; % 初始点

options = optimoptions('fmincon', 'Algorithm', 'sqp'); % 设置优化选项

[x, fval] = fmincon(@objective, x0, [], [], [], [], [], [], @nonlincon, options);

disp(['Optimal solution: x1 = ', num2str(x(1)), ', x2 = ', num2str(x(2))]);
disp(['Objective function value: ', num2str(fval)]);

% 目标函数定义
function f = objective(x)
    f = x(1)^2 + x(2)^2; % 示例目标函数：最小化 x(1)^2 + x(2)^2
end

% 非线性约束定义
function [c, ceq] = nonlincon(x)
    c = x(1)^2 + x(2)^2 - 1; % 非线性不等式约束：x(1)^2 + x(2)^2 <= 1
    ceq = []; % 没有非线性等式约束
end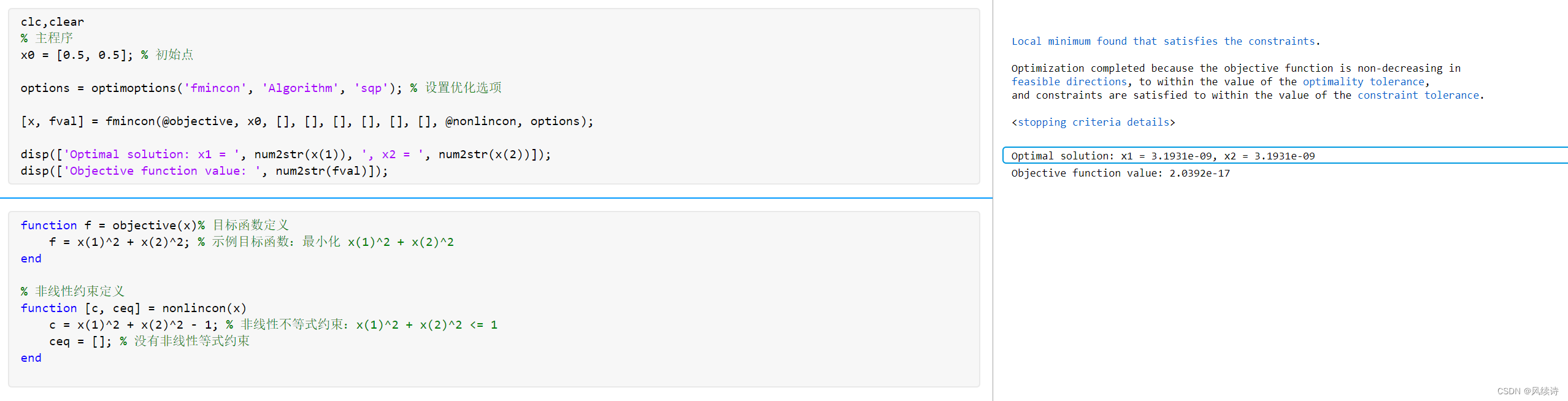

 

详细解释：

• 目标函数：objective定义了要最小化的函数。在这个例子中，它是一个简单的二次函数。
• 初始点：x0是优化变量的初始猜测值。
• 线性不等式约束：定义为A*x <= b，在这里A是一个2x2矩阵，b是一个2x1向量。
• 线性等式约束：定义为Aeq*x = beq，在这里Aeq是一个1x2矩阵，beq是一个标量。
• 变量边界：lb和ub分别是变量的下界和上界。
• 非线性约束：nonlcon定义了一个匿名函数，返回两个输出。第一个输出为空数组[]（表示没有非线性不等式约束），第二个输出是x(1)^2 + x(2)^2 - 1（表示非线性等式约束）。
• 优化选项：options使用optimoptions函数创建，用于设置优化器行为，比如显示每次迭代的信息。
• 调用fmincon：传入所有定义的参数，fmincon会返回最优解x和在最优值。

2.路径优化（以避障问题为例）

问题：假设我们有一个二维平面上的机器人从起点 ((x_0, y_0)) 移动到终点 ((x_f, y_f))。为了简化问题，我们将约束设定为机器人需要避开一个圆形障碍物，且路径应尽量短。

• 起点: ((0, 0))
• 终点: ((10, 10))
• 障碍物: 圆心在 ((5, 5))，半径为 3 的圆形区域
• 目标: 最小化路径长度

我们可以用一系列控制点来定义路径，然后通过优化这些控制点的位置来找到最优路径。假设路径由起点、终点和两个中间控制点(x1, y1)和(x2, y2)构成。

% 起点和终点
x0 = [0, 0];
xf = [10, 10];

% 初始猜测的控制点
x_initial = [2, 2, 8, 8];

% 优化选项
options = optimoptions('fmincon', 'Algorithm', 'sqp');

% 优化求解
[x_opt, fval] = fmincon(@objective, x_initial, [], [], [], [], [], [], @nonlincon, options);

% 显示结果
disp(['Optimal control points: x1 = (', num2str(x_opt(1)), ', ', num2str(x_opt(2)), ...
      '), x2 = (', num2str(x_opt(3)), ', ', num2str(x_opt(4)), ')']);
disp(['Minimum path length: ', num2str(fval)]);

% 绘图展示
figure;
hold on;
plot([x0(1), x_opt(1), x_opt(3), xf(1)], [x0(2), x_opt(2), x_opt(4), xf(2)], '-o');
viscircles([5 5], 3); % 绘制障碍物
scatter([x0(1), xf(1)], [x0(2), xf(2)], 'filled'); % 起点和终点
title('Optimal Path with Obstacle Avoidance');
xlabel('X');
ylabel('Y');
grid on;
axis equal;
hold off;

% 目标函数定义
function f = objective(x)
    x0 = [0, 0];
    xf = [10, 10];
    x1 = x(1:2);
    x2 = x(3:4);
    f = norm(x1 - x0) + norm(x2 - x1) + norm(xf - x2);
end

% 非线性约束定义
function [c, ceq] = nonlincon(x)
    % 障碍物参数
    obstacle_center = [5, 5];
    obstacle_radius = 3;

    % 控制点
    x1 = x(1:2);
    x2 = x(3:4);

    % 非线性不等式约束
    c = [norm(x1 - obstacle_center) - obstacle_radius;
         norm(x2 - obstacle_center) - obstacle_radius];
    ceq = [];
end

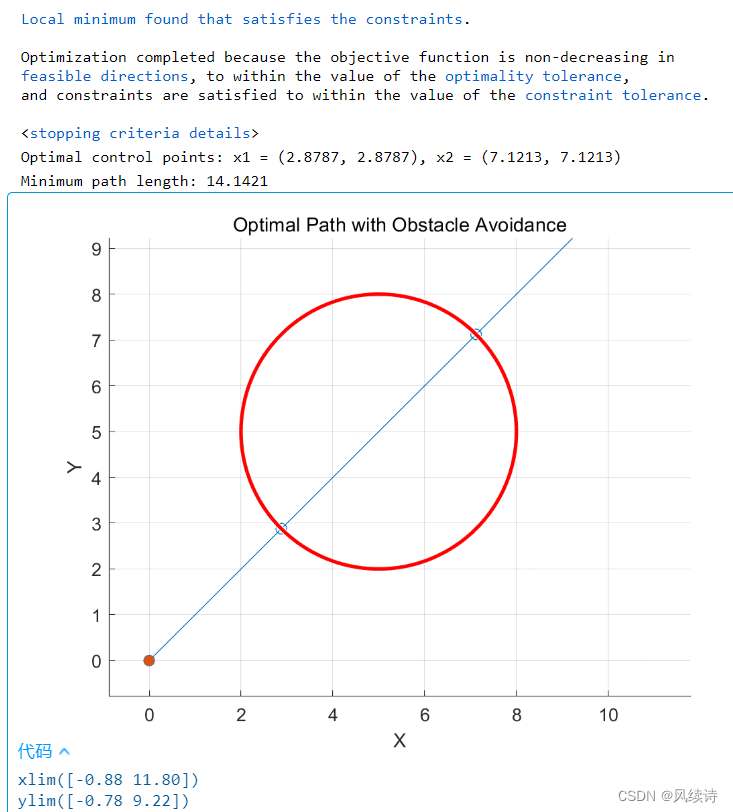
3.利润问题

问题：一家家具制造公司生产两种家具产品：沙发 ( A ) 和餐桌 ( B )。沙发和餐桌的生产利润受生产量限制，并且需要原材料和劳动力。公司希望通过调整沙发和餐桌的生产量，以最大化总利润。

公司的总利润 ( P ) 可以表示为沙发 ( A ) 和餐桌 ( B ) 利润之和。

假设利润函数为： [ P(x, y) = 800x + 600y - 2x^2 - 0.5xy - y^2 ]

• 原材料约束：生产一个沙发和一个餐桌分别需要 2 单位和 1 单位的原材料，而原材料供应上限为 200 单位。 [ 2x + y <=200 ]
• 劳动力约束：生产一个沙发和一个餐桌分别需要 3 单位和 2 单位的劳动力，而劳动力供应上限为 300 单位。 [ 3x + 2y <= 300 ]
• 非负性约束：生产量不能为负。 [ x,y >=0]

% 定义目标函数
fun = @(vars) -(800*vars(1) + 600*vars(2) - 2*vars(1)^2 - 0.5*vars(1)*vars(2) - vars(2)^2);

% 定义约束条件
A = [2, 1; 3, 2];
b = [200; 300];
lb = [0; 0];

% 非线性规划求解
options = optimoptions('fmincon', 'Algorithm', 'sqp');
[x, fval] = fmincon(fun, [1, 1], A, b, [], [], lb, [], [], options);

% 输出结果
disp('Optimal solution:');
disp(x);
disp('Maximum profit:');
disp(-fval);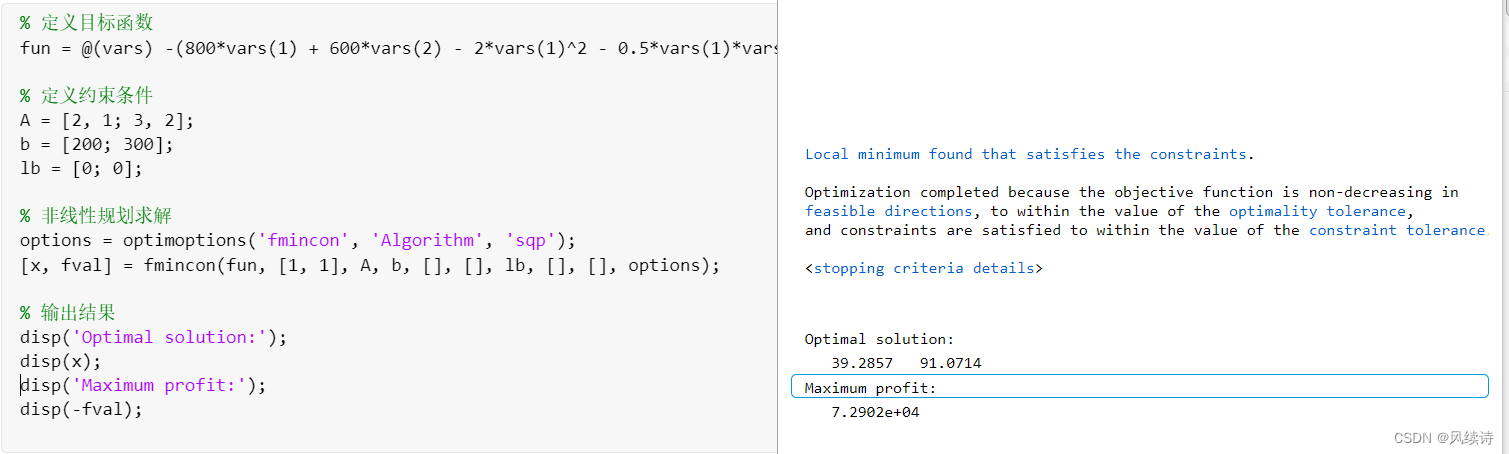

五、注意

1. 初始化参数：为了获得良好的收敛性，通常需要为变量提供一个合理的初始值。这可以通过为变量提供初始猜测值来实现。

2. 检查约束条件的可行性：在求解器开始求解之前，可以使用非线性约束和初始点来检查约束条件的可行性。这可以通过调用constrchk函数来完成。

3. 迭代改进解：对于复杂的非线性规划问题，可能需要多次迭代来改进解决方案。可以根据需要循环调用求解器，尝试不同的初始点和参数设置，以获得更好的结果。

4. 得到的最优解并不一定是这道题的最优解，需要通过循环嵌套或者改变初始值进行反复求解，一般在最后的结果中，一直是一个解，就是最优解。

总结

最需要关注的部分是非线性约束定义的处理，其中可能会牵涉到各种算法，后期本作者会写相关文章说明，读者也可以通过其他大佬的文章学习。