目录
一、引言
在市场营销当中,通过观察,我们可以看到客户的大致年龄、消费行为等信息,但是我们却很难区分它们的类别,因此可以认为它们是没有标签的数据,在观察一幅图片时,我们可以看到图片中的各种颜色,每一种颜色对应着一种数据,但是没有预测的信息,即它们也是没有标签的数据。对于上面的任务,我们只有样本x,却没有其标签y,这样的任务也不再是通过样本x去预测y,而是通过样本的特征找到样本之间的关联。由于没有标签作为监督信号,这一过程也被称为无监督学习。本文将要讲解的k均值聚类(k-Means Clustering)算法就是一个无监督学习算法。它的目标是将数据集中的样本根据其特征分为几个类,使得每一类内部样本的特征都尽可能的相近,这样的任务通常称为聚类任务。作为最简单的聚类算法,k均值聚类算法在现实中有广泛的应用。下面,我们将要详细讲解k均值算法的原理,算法以及可视化的Python代码的实现。
二、k均值聚类算法的原理
(一)数学定义
给定一组观测数据集 ,其中每个观测
是一个p维实向量,K均值聚类算法的目标是将数据集划分为k个簇
,以最小化簇内平方和(Within-Cluster Sum of Squares, WCSS):
其中,是簇
的中心(质心),定义为:
(二) 目标函数
K均值聚类是一个优化问题,目标是找到簇的划分和质心的位置,使得簇内平方和J最小。这是一个NP难问题,K均值算法采用迭代优化的方法,通常能找到一个局部最优解。
三、k均值聚类算法的步骤
(一)初始化阶段
选择k个初始簇中心(质心)。初始化方法对算法的最终结果有重要影响。常用的初始化方法有:
1. 随机选择法:从数据集中随机选择k个点作为初始质心。
2. K-means++:优化的初始化方法,通过加权概率选择相距较远的点作为初始质心。
(二)迭代优化阶段
重复执行以下两个步骤,直到满足收敛条件:
1. 分配阶段:将每个数据点分配到距离最近的质心所代表的簇。
对于每个数据点 ,计算其与各质心的距离,并将其分配给距离最近的质心所在的簇:
其中, 是第
轮迭代中第
个簇的质心。
2. 更新阶段:重新计算每个簇的质心。
对于每个簇 ,计算其新的质心:
(三)收敛条件
算法迭代直到满足以下任一条件:
1. 质心不再显著变化(质心移动距离小于预设阈值)。
2. 数据点的簇分配不再改变。
3. 达到预设的最大迭代次数。
(四) K-means++初始化
K-means++是一种改进的初始化方法,旨在选择更优的初始质心,从而提高聚类结果的质量和算法的收敛速度。算法步骤如下:
1. 随机选择第一个质心 。
2. 计算每个点 到当前已选质心集合的最短距离
。
3. 基于概率 选择下一个质心,使得距离现有质心较远的点更可能被选为下一个质心。
4. 重复步骤2和3,直到选择了 个质心。
这种方法倾向于选择彼此间距较远的点作为初始质心,避免了随机初始化可能导致的不良聚类结果。
(五) k均值聚类算法的优缺点
优点:
1. 简洁高效:算法思想简单,实现容易,计算复杂度较低。
2. 扩展性好:可处理大规模数据集。
3. 适用广泛:应用于各种领域的数据分析任务。
缺点:
1. 需要预先确定簇数k:在实际应用中,合适的簇数通常不知道。
2. 对异常值敏感:异常值会显著影响簇质心的计算。
3. 结果依赖初始质心:不同的初始质心可能导致不同的聚类结果。
4. 倾向于发现球状簇:不适合发现复杂形状的簇。
5. 容易陷入局部最优:最终结果可能不是全局最优解。
(六) 算法复杂度
1.时间复杂度:O(t·k·n·d),其中t是迭代次数,k是簇数,n是数据点数,d是维度。
2.空间复杂度:O(k+n),需要存储k个质心和n个数据点的簇标签。
四、k均值聚类算法可视化的Python代码实战
(一)Python代码实战的步骤详解
1. 数据生成与预处理
代码首先实现了多种数据生成方法,以便于测试和演示K均值聚类算法:
(1) 随机数据生成:使用generate_cluster_data函数基于scikit-learn的make_blobs函数生成可控制的聚类数据。
(2) 自定义分布生成:generate_custom_clusters函数生成特定形状的数据(如十字形分布)。
(3) 数据保存与加载:save_to_csv和load_from_csv函数用于数据的持久化存储和读取。
2. k均值聚类核心实现
k均值聚类的核心实现在KMeansClusterer类中,包含以下主要方法:
(1) 距离计算:_compute_distance方法计算数据点到质心的欧几里得距离矩阵:
def _compute_distance(self, X, centroids):
return cdist(X, centroids, 'euclidean')(2) 簇内平方和(SSE)计算:_compute_sse方法计算当前聚类的误差:
def _compute_sse(self, X, labels, centroids):
sse = 0.0
for i in range(self.n_clusters):
cluster_points = X[labels == i]
if len(cluster_points) > 0:
sse += np.sum(np.square(cdist(cluster_points, centroids[i].reshape(1, -1))))
return sse(3) 质心初始化:
a.随机初始化:_init_random方法随机选择数据点作为初始质心。
b.K-means++初始化:_init_kmeans_plus_plus方法实现了K-means++初始化策略。
(4) 聚类过程:fit方法实现了迭代聚类过程,每次迭代都包含:
a.分配数据点到最近的质心。
b.重新计算每个簇的质心。
c. 计算SSE并检查收敛条件。
3.可视化实现
代码实现了多种可视化方法,以帮助理解K均值聚类的工作原理:
(1) 基础聚类可视化:show_cluster函数展示聚类结果,支持2D和3D数据:
a. 2D数据使用Matplotlib绘制散点图。
b.3D数据使用Plotly创建交互式3D散点图。
(2) 聚类过程动态可视化:visualize_kmeans_animation函数展示算法迭代过程:
a.2D数据使用Matplotlib的FuncAnimation创建动画。
b.3D数据使用Plotly的Frames机制创建交互式动画,支持播放、暂停和帧滑动。
(3) 初始化方法对比可视化:visualize_initialization_comparison函数比较随机初始化和K-means++初始化的效果:
a.质心轨迹对比。
b.聚类结果对比。
c.SSE收敛速度对比。
(4) 簇内误差分布可视化:visualize_cluster_errors函数展示聚类误差分布:
a.使用点大小表示误差大小。
b.提供误差直方图和箱线图。
4.详细算法步骤解析
4.1 K-means++初始化算法在代码中的实现如下:
def _init_kmeans_plus_plus(self, X):
n_samples, n_features = X.shape
centroids = np.zeros((self.n_clusters, n_features))
# 随机选择第一个中心点
first_idx = np.random.choice(n_samples)
centroids[0] = X[first_idx].copy()
# 选择剩余的中心点
for c in range(1, self.n_clusters):
# 计算每个点到已有中心点的最小距离
dist_sq = np.min(self._compute_distance(X, centroids[:c]), axis=1) ** 2
# 将距离平方作为概率权重
probs = dist_sq / dist_sq.sum()
# 按概率选择下一个中心点
cumulative_probs = np.cumsum(probs)
r = np.random.rand()
for j, p in enumerate(cumulative_probs):
if r < p:
centroids[c] = X[j].copy()
break
return centroids该算法的数学步骤为:
(1) 随机选择第一个质心
(2) 对于每个数据点 ,计算它到最近已选质心的距离:
(3) 计算选择概率:
(4) 按照概率 选择下一个质心。
(5) 重复步骤2-4直到选择了 个质心。
4.2 K均值聚类迭代过程详解
迭代聚类过程在fit方法中实现:
def fit(self, X):
# 初始化聚类中心
self.centroids = self._init_centroids(X)
previous_centroids = None
self.history = [] # 清空历史记录
self.sse_history = [] # 清空SSE历史
# 迭代优化
for iter_num in range(self.max_iters):
# 分配样本到簇
distances = self._compute_distance(X, self.centroids)
self.labels = np.argmin(distances, axis=1)
# 更新聚类中心
previous_centroids = self.centroids.copy()
for i in range(self.n_clusters):
cluster_points = X[self.labels == i]
if len(cluster_points) > 0:
self.centroids[i] = np.mean(cluster_points, axis=0)
# 计算当前SSE
current_sse = self._compute_sse(X, self.labels, self.centroids)
self.sse_history.append(current_sse)
# 保存当前状态到历史记录
self.history.append({
'centroids': self.centroids.copy(),
'labels': self.labels.copy(),
'sse': current_sse
})
# 判断是否收敛
centroid_shift = np.linalg.norm(self.centroids - previous_centroids)
if centroid_shift < self.tol:
break该过程对应的数学步骤为:
(1) 初始化:选择 个初始质心
(2) 迭代:对于第 次迭代:
分配:对每个点 ,计算到各质心的距离
,将
分配到最近的质心所代表的簇:
更新:重新计算每个簇的质心:
评估:计算簇内平方和误差(SSE):
收敛检查:如果质心变化小于阈值 ,即
,则停止迭代
4.3 可视化技术详解
4.3.1 3D聚类可视化(Plotly实现)
3D聚类结果可视化使用Plotly实现,关键代码如下:
# 创建Plotly图形
fig = go.Figure()
# 添加每个簇的数据点
for i, cls in enumerate(clusters):
cluster_points = dataset[cluster == cls]
fig.add_trace(go.Scatter3d(
x=cluster_points[:, 0],
y=cluster_points[:, 1],
z=cluster_points[:, 2],
mode='markers',
marker=dict(
size=5,
color=colors[i % len(colors)],
opacity=0.7
),
name=f'簇 {cls+1}'
))
# 添加聚类中心
if centroids is not None:
fig.add_trace(go.Scatter3d(
x=centroids[:, 0],
y=centroids[:, 1],
z=centroids[:, 2],
mode='markers',
marker=dict(
size=10,
color='black',
symbol='x'
),
name='聚类中心'
))4.3.2 聚类过程动态可视化(Plotly实现)
3D聚类过程的动态可视化使用Plotly的Frames功能实现,关键代码如下:
# 创建一个包含所有帧的Plotly动画
frames = []
# 准备数据
for i, state in enumerate(kmeans.history):
frame_data = []
centroids = state['centroids']
labels = state['labels']
# 添加各个簇的点和质心
for cls in range(kmeans.n_clusters):
cluster_points = X[labels == cls]
if len(cluster_points) > 0:
frame_data.append(go.Scatter3d(...))
# 添加质心
frame_data.append(go.Scatter3d(...))
# 创建帧
frames.append(go.Frame(
data=frame_data,
name=f'frame{i}'
))
# 创建初始视图
fig = go.Figure(
data=frames[0].data,
frames=frames
)
# 添加播放控件和滑动条
fig.update_layout(
updatemenus=[{
'type': 'buttons',
'buttons': [
{'label': '播放', 'method': 'animate', ...},
{'label': '暂停', 'method': 'animate', ...}
]
}],
sliders=[{
'steps': [
{'method': 'animate', 'label': f'{i+1}', ...}
for i in range(len(frames))
]
}]
)4.4算法执行流程
完整的算法执行流程包含以下步骤:
(1) 数据准备:生成或加载聚类数据。
(2)基本聚类:使用随机初始化执行K均值聚类。
(3) 改进聚类:使用K-means++初始化执行K均值聚类。
(4) 可视化分析:
a.对比随机初始化与K-means++初始化的效果。
b.动态可视化聚类过程。
c.分析聚类误差分布。
4.5. 3D数据分析:对3D数据执行K均值聚类并进行可视化。
整个流程在main函数中实现:
def main():
# 1. 数据准备
X_2d, y_2d = generate_custom_clusters()
save_to_csv(X_2d, 'kmeans_data.csv')
dataset = load_from_csv('kmeans_data.csv')
# 2. 基本聚类
kmeans_random = KMeansClusterer(n_clusters=4, init_method='random', random_state=42)
kmeans_random.fit(dataset)
show_cluster(dataset, kmeans_random.labels, kmeans_random.centroids, title="K均值聚类结果 (随机初始化)")
# 3. 改进聚类
kmeans_pp = KMeansClusterer(n_clusters=4, init_method='k-means++', random_state=42)
kmeans_pp.fit(dataset)
show_cluster(dataset, kmeans_pp.labels, kmeans_pp.centroids, title="K均值聚类结果 (K-means++初始化)")
# 4. 可视化分析
visualize_initialization_comparison(dataset, k=4)
visualize_kmeans_animation(dataset, kmeans_pp, interval=1000)
visualize_cluster_errors(dataset, kmeans_pp)
# 5. 3D数据分析
X_3d, y_3d = generate_cluster_data(n_samples=500, n_features=3, centers=4, cluster_std=0.8)
kmeans_3d = KMeansClusterer(n_clusters=4, init_method='k-means++', random_state=42)
kmeans_3d.fit(X_3d)
show_cluster(X_3d, kmeans_3d.labels, kmeans_3d.centroids, title="3D K均值聚类结果")
visualize_kmeans_animation(X_3d, kmeans_3d, interval=1000)(二)Python代码的实现
先运行"随机生成k均值聚类数据集.py"的代码,再运行"k均值聚类.py"的代码,"随机生成k均值聚类数据集.py"文件与"k均值聚类.py"文件应位于同一目录中。

随机生成k均值聚类数据集.py
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
def generate_cluster_data(n_samples=500, n_features=2, centers=4, cluster_std=1.0, random_state=42):
"""
生成适合K均值聚类的模拟数据集
参数:
n_samples (int): 样本总数
n_features (int): 特征维度,默认2维便于可视化
centers (int): 生成的簇数量
cluster_std (float): 簇内数据的标准差,控制簇的紧密程度
random_state (int): 随机种子,保证结果可复现
返回:
X (ndarray): 生成的特征数据,形状为(n_samples, n_features)
y (ndarray): 真实的簇标签,形状为(n_samples,)
"""
print(f"生成数据集: {n_samples}个样本, {n_features}维特征, {centers}个簇...")
X, y = make_blobs(n_samples=n_samples,
n_features=n_features,
centers=centers,
cluster_std=cluster_std,
random_state=random_state)
return X, y
def generate_custom_clusters():
"""
生成一个包含4个明显分散的簇的二维数据集
返回:
X: 形状为(500, 2)的numpy数组,表示500个二维数据点
y: 簇标签
"""
# 设置随机种子以保证结果可复现
np.random.seed(42)
# 簇中心点坐标
centers = [
[3, 3], # 第一个簇中心
[-3, 3], # 第二个簇中心
[-3, -3], # 第三个簇中心
[3, -3] # 第四个簇中心
]
# 每个簇的样本数
n_samples_per_cluster = 125
# 簇的标准差(控制簇的紧密程度)
cluster_std = 0.8
# 创建空数组存储所有数据点和标签
X = np.zeros((n_samples_per_cluster * len(centers), 2))
y = np.zeros(n_samples_per_cluster * len(centers), dtype=int)
# 生成每个簇的数据点
for i, (cx, cy) in enumerate(centers):
# 生成正态分布的点,围绕簇中心
start_idx = i * n_samples_per_cluster
end_idx = start_idx + n_samples_per_cluster
# 簇内x坐标的正态分布
X[start_idx:end_idx, 0] = np.random.normal(cx, cluster_std, n_samples_per_cluster)
# 簇内y坐标的正态分布
X[start_idx:end_idx, 1] = np.random.normal(cy, cluster_std, n_samples_per_cluster)
# 设置簇标签
y[start_idx:end_idx] = i
# 随机打乱数据点顺序
indices = np.arange(len(X))
np.random.shuffle(indices)
X = X[indices]
y = y[indices]
print(f"生成数据集: 500个样本, 2维特征, 4个簇...")
return X, y
def save_to_csv(X, filename='kmeans_data.csv'):
"""
将生成的数据保存为CSV文件
参数:
X (ndarray): 特征数据
filename (str): 保存文件名
"""
# 保存为CSV
np.savetxt(filename, X, delimiter=',')
print(f"数据已保存至: {filename}")
return True
def load_from_csv(filename='kmeans_data.csv'):
"""
从CSV文件加载数据
参数:
filename (str): 数据文件名
返回:
X (ndarray): 加载的数据
"""
try:
dataset = np.loadtxt(filename, delimiter=',')
print(f'成功加载数据集: {filename}, 大小: {len(dataset)}')
return dataset
except Exception as e:
print(f"加载数据失败: {e}")
return None
def visualize_data(X, y=None, title="生成的聚类数据"):
"""
可视化生成的数据集
参数:
X: 要可视化的数据集
y: 簇标签(可选)
title: 图表标题
"""
plt.figure(figsize=(10, 8))
if y is not None:
# 如果提供了标签,使用不同的颜色表示不同的簇
colors = ['#4EACC5', '#FF9C34', '#4E9A06', '#9A4EAE', '#C53434', '#34C5FF']
for i in np.unique(y):
plt.scatter(
X[y == i, 0], X[y == i, 1],
s=50, alpha=0.8,
c=colors[i % len(colors)],
label=f'簇 {i + 1}'
)
plt.legend()
else:
# 否则使用单一颜色
plt.scatter(X[:, 0], X[:, 1], s=50, alpha=0.8, c='skyblue', edgecolors='gray')
plt.title(title, fontsize=15)
plt.xlabel('特征1', fontsize=12)
plt.ylabel('特征2', fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()
plt.show()
if __name__ == "__main__":
# 生成方法1:使用sklearn的make_blobs生成数据
X1, y1 = generate_cluster_data(n_samples=500, n_features=2, centers=4, cluster_std=0.8)
visualize_data(X1, y1, "使用make_blobs生成的聚类数据")
# 生成方法2:使用自定义分布生成数据
X2, y2 = generate_custom_clusters()
visualize_data(X2, y2, "使用自定义方法生成的聚类数据")
# 保存数据(这里选择保存自定义生成的数据)
save_to_csv(X2, 'kmeans_data.csv')
# 测试加载数据
loaded_data = load_from_csv('kmeans_data.csv')
if loaded_data is not None:
visualize_data(loaded_data, title="从CSV加载的数据")
k均值聚类.py
import os
import sys
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from mpl_toolkits.mplot3d import Axes3D # 3D绘图必须导入
import pandas as pd
from scipy.spatial.distance import cdist
import time
import warnings
# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
warnings.filterwarnings('ignore') # 忽略警告信息
# 导入Plotly用于3D可视化
import plotly.graph_objects as go
from plotly.subplots import make_subplots
import plotly.express as px
# 尝试导入数据生成模块
try:
from 随机生成k均值聚类数据集 import generate_cluster_data, generate_custom_clusters
from 随机生成k均值聚类数据集 import save_to_csv, load_from_csv, visualize_data
data_module_imported = True
except ImportError:
print("无法导入数据生成模块,将使用内置的数据生成函数")
# 如果导入失败,定义简化的数据生成函数
def generate_cluster_data(n_samples=500, n_features=2, centers=4, cluster_std=1.0, random_state=42):
"""简化版数据生成函数"""
# 设置随机种子
np.random.seed(random_state)
# 生成簇中心
if isinstance(centers, int):
centers_coords = np.random.uniform(-5, 5, (centers, n_features))
else:
centers_coords = np.array(centers)
centers = len(centers_coords)
# 生成数据点
X = np.zeros((n_samples, n_features))
y = np.zeros(n_samples, dtype=int)
samples_per_center = n_samples // centers
for i, center in enumerate(centers_coords):
start_idx = i * samples_per_center
end_idx = start_idx + samples_per_center if i < centers - 1 else n_samples
X[start_idx:end_idx] = np.random.normal(center, cluster_std, (end_idx - start_idx, n_features))
y[start_idx:end_idx] = i
# 随机打乱数据
idx = np.random.permutation(n_samples)
X, y = X[idx], y[idx]
print(f"生成数据集: {n_samples}个样本, {n_features}维特征, {centers}个簇...")
return X, y
def generate_custom_clusters():
"""生成十字形分布的聚类数据"""
# 设置随机种子
np.random.seed(42)
# 簇中心点坐标
centers = [
[3, 3], # 第一个簇中心
[-3, 3], # 第二个簇中心
[-3, -3], # 第三个簇中心
[3, -3] # 第四个簇中心
]
# 每个簇的样本数
n_samples_per_cluster = 125
# 簇的标准差
cluster_std = 0.8
# 生成数据
X = np.zeros((n_samples_per_cluster * len(centers), 2))
y = np.zeros(n_samples_per_cluster * len(centers), dtype=int)
for i, (cx, cy) in enumerate(centers):
start_idx = i * n_samples_per_cluster
end_idx = start_idx + n_samples_per_cluster
X[start_idx:end_idx, 0] = np.random.normal(cx, cluster_std, n_samples_per_cluster)
X[start_idx:end_idx, 1] = np.random.normal(cy, cluster_std, n_samples_per_cluster)
y[start_idx:end_idx] = i
# 打乱顺序
idx = np.random.permutation(len(X))
X, y = X[idx], y[idx]
print(f"生成数据集: 500个样本, 2维特征, 4个簇...")
return X, y
def save_to_csv(X, filename='kmeans_data.csv'):
"""保存数据到CSV文件"""
np.savetxt(filename, X, delimiter=',')
print(f"数据已保存至: {filename}")
return True
def load_from_csv(filename='kmeans_data.csv'):
"""从CSV文件加载数据"""
try:
dataset = np.loadtxt(filename, delimiter=',')
print(f'成功加载数据集: {filename}, 大小: {len(dataset)}')
return dataset
except Exception as e:
print(f"加载数据失败: {e}")
return None
def visualize_data(X, y=None, title="生成的聚类数据"):
"""可视化数据"""
plt.figure(figsize=(10, 8))
if y is not None:
colors = ['#4EACC5', '#FF9C34', '#4E9A06', '#9A4EAE', '#C53434', '#34C5FF']
for i in np.unique(y):
plt.scatter(
X[y == i, 0], X[y == i, 1],
s=50, alpha=0.8,
c=colors[i % len(colors)],
label=f'簇 {i + 1}'
)
plt.legend()
else:
plt.scatter(X[:, 0], X[:, 1], s=50, alpha=0.8, c='skyblue', edgecolors='gray')
plt.title(title, fontsize=15)
plt.xlabel('特征1', fontsize=12)
plt.ylabel('特征2', fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()
plt.show()
data_module_imported = False
# ==============================
# K均值聚类算法核心类
# ==============================
class KMeansClusterer:
"""
K均值聚类算法的完整实现,支持可视化
参数:
n_clusters: 聚类簇数,默认为4
max_iters: 最大迭代次数,默认为50
init_method: 初始化方法,'random'或'k-means++'
tol: 收敛阈值,当质心移动小于此值时认为收敛
verbose: 是否打印过程信息
random_state: 随机数种子
"""
def __init__(self, n_clusters=4, max_iters=50, init_method='random', tol=1e-4, verbose=True, random_state=None):
self.n_clusters = n_clusters # 簇数量
self.max_iters = max_iters # 最大迭代次数
self.init_method = init_method # 初始化方法
self.tol = tol # 收敛阈值
self.verbose = verbose # 是否输出详细信息
self.centroids = None # 聚类中心点
self.labels = None # 样本标签
self.inertia = None # 聚类误差(簇内平方和)
self.n_iter = 0 # 实际迭代次数
self.history = [] # 迭代过程记录
self.sse_history = [] # SSE历史记录
# 设置随机种子
if random_state is not None:
np.random.seed(random_state)
def _compute_distance(self, X, centroids):
"""计算样本点到聚类中心的距离"""
return cdist(X, centroids, 'euclidean')
def _compute_sse(self, X, labels, centroids):
"""计算簇内平方和误差(Sum of Squared Errors, SSE)"""
sse = 0.0
for i in range(self.n_clusters):
cluster_points = X[labels == i]
if len(cluster_points) > 0:
sse += np.sum(np.square(cdist(cluster_points, centroids[i].reshape(1, -1))))
return sse
# ==== 初始化方法 ====
def _init_random(self, X):
"""随机初始化聚类中心"""
idx = np.random.choice(X.shape[0], self.n_clusters, replace=False)
return X[idx].copy()
def _init_kmeans_plus_plus(self, X):
"""K-means++初始化聚类中心
原理:
1. 随机选择第一个聚类中心
2. 计算每个点到当前所有聚类中心的最小距离
3. 按照距离的平方作为概率权重选择下一个聚类中心
4. 重复步骤2-3直到选择了k个聚类中心
这种方法倾向于选择彼此间距较远的聚类中心,通常能减少迭代次数和提高聚类质量
"""
n_samples, n_features = X.shape
centroids = np.zeros((self.n_clusters, n_features))
# 随机选择第一个中心点
first_idx = np.random.choice(n_samples)
centroids[0] = X[first_idx].copy()
# 选择剩余的中心点
for c in range(1, self.n_clusters):
# 计算每个点到已有中心点的最小距离
dist_sq = np.min(self._compute_distance(X, centroids[:c]), axis=1) ** 2
# 将距离平方作为概率权重
probs = dist_sq / dist_sq.sum()
# 按概率选择下一个中心点
cumulative_probs = np.cumsum(probs)
r = np.random.rand()
for j, p in enumerate(cumulative_probs):
if r < p:
centroids[c] = X[j].copy()
break
return centroids
def _init_centroids(self, X):
"""根据指定方法初始化聚类中心"""
if self.init_method.lower() == 'k-means++':
if self.verbose:
print("使用K-means++初始化聚类中心...")
return self._init_kmeans_plus_plus(X)
else: # 默认随机初始化
if self.verbose:
print("使用随机方法初始化聚类中心...")
return self._init_random(X)
# ==== 核心聚类过程 ====
def fit(self, X):
"""
执行K均值聚类算法
参数:
X: 数据集,形状为(n_samples, n_features)
返回:
self: 训练好的聚类器
"""
# 初始化聚类中心
self.centroids = self._init_centroids(X)
previous_centroids = None
self.history = [] # 清空历史记录
self.sse_history = [] # 清空SSE历史
start_time = time.time()
# 迭代优化
for iter_num in range(self.max_iters):
# 分配样本到簇
distances = self._compute_distance(X, self.centroids)
self.labels = np.argmin(distances, axis=1)
# 更新聚类中心
previous_centroids = self.centroids.copy()
for i in range(self.n_clusters):
cluster_points = X[self.labels == i]
if len(cluster_points) > 0:
self.centroids[i] = np.mean(cluster_points, axis=0)
# 计算当前SSE
current_sse = self._compute_sse(X, self.labels, self.centroids)
self.sse_history.append(current_sse)
# 保存当前状态到历史记录
self.history.append({
'centroids': self.centroids.copy(),
'labels': self.labels.copy(),
'sse': current_sse
})
# 判断是否收敛
centroid_shift = np.linalg.norm(self.centroids - previous_centroids)
if self.verbose:
print(f"迭代 {iter_num + 1}: SSE = {current_sse:.4f}, 质心移动距离 = {centroid_shift:.6f}")
if centroid_shift < self.tol:
if self.verbose:
print(f"算法在第{iter_num + 1}次迭代后收敛")
break
# 记录迭代次数和最终SSE
self.n_iter = iter_num + 1
self.inertia = self.sse_history[-1]
end_time = time.time()
if self.verbose:
print(f"K均值聚类完成,用时 {end_time - start_time:.4f} 秒")
print(f"总迭代次数: {self.n_iter}, 最终SSE: {self.inertia:.4f}")
return self
def predict(self, X):
"""
预测新数据的簇分配
参数:
X: 待预测数据,形状为(n_samples, n_features)
返回:
labels: 簇标签,形状为(n_samples,)
"""
if self.centroids is None:
raise ValueError("模型尚未训练,请先调用fit方法")
distances = self._compute_distance(X, self.centroids)
return np.argmin(distances, axis=1)
def fit_predict(self, X):
"""
训练模型并预测簇分配
参数:
X: 数据集,形状为(n_samples, n_features)
返回:
labels: 簇标签,形状为(n_samples,)
"""
self.fit(X)
return self.labels
# ==============================
# 基础可视化函数
# ==============================
def show_cluster(dataset, cluster, centroids=None, title=None, save_fig=False, filename=None):
"""
可视化聚类结果
参数:
dataset: 数据集,形状为(n_samples, n_features)
cluster: 簇标签,形状为(n_samples,)
centroids: 聚类中心点坐标,如果为None则不显示
title: 图表标题
save_fig: 是否保存图像
filename: 图像保存路径
"""
# 获取数据维度
n_dim = dataset.shape[1]
# 不同种类的颜色和形状,用以区分划分的数据类别
colors = ['#4EACC5', '#FF9C34', '#4E9A06', '#9A4EAE', '#C53434', '#34C5FF']
markers = ['o', '^', 's', 'd', 'p', '*']
if n_dim <= 2: # 2D可视化 - 使用Matplotlib
# 创建画布
plt.figure(figsize=(10, 7))
# 获取不同的簇
clusters = np.unique(cluster)
K = len(clusters)
# 画出所有样例
for i, cls in enumerate(clusters):
plt.scatter(
dataset[cluster == cls, 0],
dataset[cluster == cls, 1] if n_dim > 1 else np.zeros(np.sum(cluster == cls)),
s=50,
c=colors[i % len(colors)],
marker=markers[i % len(markers)],
label=f'簇 {cls + 1}'
)
# 画出中心点
if centroids is not None:
plt.scatter(
centroids[:, 0],
centroids[:, 1] if n_dim > 1 else np.zeros(len(centroids)),
s=200,
c='black',
marker='X',
label='聚类中心'
)
plt.grid(True, linestyle='--', alpha=0.7)
plt.legend()
plt.title(title if title else f"K均值聚类结果 (k={K})")
plt.tight_layout()
if save_fig and filename:
plt.savefig(filename, dpi=300, bbox_inches='tight')
plt.show()
elif n_dim == 3: # 3D可视化 - 使用Plotly
# 获取不同的簇
clusters = np.unique(cluster)
K = len(clusters)
# 创建Plotly图形
fig = go.Figure()
# 添加每个簇的数据点
for i, cls in enumerate(clusters):
cluster_points = dataset[cluster == cls]
fig.add_trace(go.Scatter3d(
x=cluster_points[:, 0],
y=cluster_points[:, 1],
z=cluster_points[:, 2],
mode='markers',
marker=dict(
size=5,
color=colors[i % len(colors)],
symbol='circle',
opacity=0.7,
line=dict(width=0.5, color='white')
),
name=f'簇 {cls + 1}'
))
# 添加聚类中心
if centroids is not None:
fig.add_trace(go.Scatter3d(
x=centroids[:, 0],
y=centroids[:, 1],
z=centroids[:, 2],
mode='markers',
marker=dict(
size=10,
color='black',
symbol='x',
line=dict(width=2, color='black')
),
name='聚类中心'
))
# 设置图形布局
fig.update_layout(
title=title if title else f"K均值聚类结果 (k={K})",
scene=dict(
xaxis_title='特征1',
yaxis_title='特征2',
zaxis_title='特征3',
aspectmode='cube'
),
legend=dict(
yanchor="top",
y=0.99,
xanchor="left",
x=0.01
),
margin=dict(l=0, r=0, b=0, t=30)
)
if save_fig and filename:
fig.write_image(filename, width=1000, height=800)
fig.show()
else:
print("Error: 仅支持2D和3D数据可视化")
return
# ==============================
# 高级可视化功能
# ==============================
def visualize_kmeans_animation(X, kmeans, interval=500, save_animation=False, filename=None):
"""
动态可视化K均值聚类过程 - 支持2D和3D数据可视化
参数:
X: 数据集,形状为(n_samples, n_features)
kmeans: 已训练的KMeansClusterer对象
interval: 帧间隔时间(毫秒)- 仅用于Matplotlib
save_animation: 是否保存动画
filename: 动画保存路径
"""
# 确保模型已训练
if not kmeans.history:
print("错误: 模型未训练或训练过程未记录历史数据")
return
# 获取数据维度
n_dim = X.shape[1]
if n_dim > 3:
print("错误: 仅支持2D和3D数据可视化")
return
# 颜色和标记
colors = ['#4EACC5', '#FF9C34', '#4E9A06', '#9A4EAE', '#C53434', '#34C5FF']
markers = ['o', '^', 's', 'd', 'p', '*']
if n_dim <= 2: # 2D可视化 - 使用Matplotlib动画
# 创建画布
fig = plt.figure(figsize=(12, 8))
# 创建布局: 上面是聚类过程,下面是SSE曲线
ax_cluster = fig.add_subplot(211) # 上半部分: 聚类过程
ax_sse = fig.add_subplot(212) # 下半部分: SSE曲线
# 为SSE曲线设置轴
max_sse = max(kmeans.sse_history) * 1.1
min_sse = min(kmeans.sse_history) * 0.9
ax_sse.set_xlim(0, len(kmeans.history))
ax_sse.set_ylim(min_sse, max_sse)
ax_sse.set_xlabel('迭代次数')
ax_sse.set_ylabel('簇内平方和 (SSE)')
ax_sse.set_title('收敛过程')
ax_sse.grid(True, linestyle='--', alpha=0.7)
# SSE线初始化
line, = ax_sse.plot([], [], 'r-o', linewidth=2, alpha=0.8)
iter_text = ax_sse.text(0.02, 0.95, '', transform=ax_sse.transAxes)
# 聚类可视化区设置
ax_cluster.set_xlim(np.min(X[:, 0]) - 1, np.max(X[:, 0]) + 1)
if n_dim == 2:
ax_cluster.set_ylim(np.min(X[:, 1]) - 1, np.max(X[:, 1]) + 1)
ax_cluster.set_xlabel('特征1')
ax_cluster.set_ylabel('特征2' if n_dim == 2 else '')
ax_cluster.grid(True, linestyle='--', alpha=0.7)
# 初始化散点和中心点
if n_dim == 1:
scatter = ax_cluster.scatter(X[:, 0], np.zeros(len(X)), s=50, c='gray', alpha=0.5)
centroids_scatter = ax_cluster.scatter([], [], s=200, c='black', marker='X')
else: # n_dim == 2
scatter = ax_cluster.scatter(X[:, 0], X[:, 1], s=50, c='gray', alpha=0.5)
centroids_scatter = ax_cluster.scatter([], [], s=200, c='black', marker='X')
# 设置标题
ax_cluster.set_title(f"K均值聚类过程 ({kmeans.init_method}初始化, k={kmeans.n_clusters})")
# 准备初始文本
status_text = ax_cluster.text(0.02, 0.95, '', transform=ax_cluster.transAxes)
# 先绘制一次基本框架,确保图像显示正确
plt.tight_layout()
plt.draw()
# 更新函数
def update(frame):
artists = []
if frame < len(kmeans.history):
# 获取当前状态
current = kmeans.history[frame]
centroids = current['centroids']
labels = current['labels']
sse = current['sse']
# 更新散点标签颜色
scatter.set_color([colors[l % len(colors)] for l in labels])
centroids_scatter.set_offsets(
centroids if n_dim == 2 else np.column_stack([centroids[:, 0], np.zeros(len(centroids))]))
status_text.set_text(f'迭代: {frame + 1}, SSE: {sse:.4f}')
artists.extend([scatter, centroids_scatter, status_text])
# 更新SSE曲线
x_data = range(frame + 1)
y_data = kmeans.sse_history[:frame + 1]
line.set_data(x_data, y_data)
iter_text.set_text(f'总迭代: {frame + 1}/{len(kmeans.history)}')
artists.extend([line, iter_text])
return artists
# 创建动画,确保动画不被垃圾回收
anim = FuncAnimation(fig, update, frames=len(kmeans.history), interval=interval, blit=True)
# 保存动画
if save_animation and filename:
anim.save(filename, writer='pillow', fps=30)
plt.tight_layout()
plt.show()
return anim
elif n_dim == 3: # 3D可视化 - 使用Plotly动态图表
# 创建一个包含所有帧的Plotly动画
frames = []
# 准备数据
for i, state in enumerate(kmeans.history):
frame_data = []
centroids = state['centroids']
labels = state['labels']
sse = state['sse']
# 添加各个簇的点
for cls in range(kmeans.n_clusters):
cluster_points = X[labels == cls]
if len(cluster_points) > 0:
frame_data.append(
go.Scatter3d(
x=cluster_points[:, 0],
y=cluster_points[:, 1],
z=cluster_points[:, 2],
mode='markers',
marker=dict(
size=5,
color=colors[cls % len(colors)],
opacity=0.7
),
name=f'簇 {cls + 1}',
showlegend=(i == 0) # 只在第一帧显示图例
)
)
# 添加质心
frame_data.append(
go.Scatter3d(
x=centroids[:, 0],
y=centroids[:, 1],
z=centroids[:, 2],
mode='markers',
marker=dict(
size=10,
color='black',
symbol='x',
line=dict(width=2, color='black')
),
name='聚类中心',
showlegend=(i == 0) # 只在第一帧显示图例
)
)
# 创建帧
frames.append(go.Frame(
data=frame_data,
name=f'frame{i}',
traces=list(range(kmeans.n_clusters + 1)) # 指定要更新的轨迹
))
# 创建初始视图(使用第一帧的数据)
fig = go.Figure(
data=frames[0].data,
frames=frames
)
# 添加标题和布局
fig.update_layout(
title=f"K均值聚类过程 ({kmeans.init_method}初始化, k={kmeans.n_clusters})",
scene=dict(
xaxis_title='特征1',
yaxis_title='特征2',
zaxis_title='特征3'
),
updatemenus=[{
'type': 'buttons',
'buttons': [
{
'label': '播放',
'method': 'animate',
'args': [None, {'frame': {'duration': 500, 'redraw': True}, 'fromcurrent': True}]
},
{
'label': '暂停',
'method': 'animate',
'args': [[None], {'frame': {'duration': 0, 'redraw': True}, 'mode': 'immediate',
'transition': {'duration': 0}}]
}
],
'direction': 'left',
'pad': {'r': 10, 't': 10},
'x': 0.1,
'y': 0,
'xanchor': 'right',
'yanchor': 'top'
}]
)
# 添加滑动条以手动浏览帧
fig.update_layout(
sliders=[{
'active': 0,
'yanchor': 'top',
'xanchor': 'left',
'currentvalue': {
'prefix': '迭代: ',
'xanchor': 'right'
},
'pad': {'b': 10, 't': 50},
'len': 0.9,
'x': 0.1,
'y': 0,
'steps': [
{
'method': 'animate',
'label': f'{i + 1}',
'args': [
[f'frame{i}'],
{'frame': {'duration': 300, 'easing': 'cubic-in-out', 'redraw': True},
'transition': {'duration': 300}}
]
}
for i in range(len(frames))
]
}]
)
# 添加SSE曲线子图
sse_values = np.array([h['sse'] for h in kmeans.history])
iterations = np.arange(1, len(sse_values) + 1)
# 创建带有SSE曲线的新图形
fig2 = make_subplots(
rows=2, cols=1,
subplot_titles=(f"K均值聚类过程 ({kmeans.init_method}初始化, k={kmeans.n_clusters})", "收敛过程 (SSE)"),
specs=[[{"type": "scene"}], [{"type": "xy"}]],
row_heights=[0.7, 0.3]
)
# 将3D聚类数据复制到新图形
for trace in fig.data:
fig2.add_trace(trace, row=1, col=1)
# 添加SSE曲线
fig2.add_trace(
go.Scatter(
x=iterations,
y=sse_values,
mode='lines+markers',
name='SSE',
marker=dict(color='red'),
line=dict(color='red', width=2)
),
row=2, col=1
)
# 移植帧数据到新图形
fig2.frames = fig.frames
# 更新布局
fig2.update_layout(
scene=dict(
xaxis_title='特征1',
yaxis_title='特征2',
zaxis_title='特征3'
),
xaxis=dict(title='迭代次数'),
yaxis=dict(title='簇内平方和 (SSE)'),
updatemenus=[{
'type': 'buttons',
'buttons': [
{
'label': '播放',
'method': 'animate',
'args': [None, {'frame': {'duration': 500, 'redraw': True}, 'fromcurrent': True}]
},
{
'label': '暂停',
'method': 'animate',
'args': [[None], {'frame': {'duration': 0, 'redraw': True}, 'mode': 'immediate',
'transition': {'duration': 0}}]
}
],
'direction': 'left',
'pad': {'r': 10, 't': 10},
'x': 0.1,
'y': 0,
'xanchor': 'right',
'yanchor': 'top'
}],
sliders=[{
'active': 0,
'yanchor': 'top',
'xanchor': 'left',
'currentvalue': {
'prefix': '迭代: ',
'xanchor': 'right'
},
'pad': {'b': 10, 't': 50},
'len': 0.9,
'x': 0.1,
'y': 0,
'steps': [
{
'method': 'animate',
'label': f'{i + 1}',
'args': [
[f'frame{i}'],
{'frame': {'duration': 300, 'easing': 'cubic-in-out', 'redraw': True},
'transition': {'duration': 300}}
]
}
for i in range(len(frames))
]
}],
height=900, # 增加图表高度以适应两个子图
margin=dict(l=50, r=50, t=50, b=50)
)
# 保存为HTML文件
if save_animation and filename:
fig2.write_html(filename)
fig2.show()
return fig2
else:
print("错误: 仅支持2D和3D数据可视化")
return None
def visualize_initialization_comparison(X, k=4, random_state=42):
"""
可视化比较随机初始化和K-means++初始化的效果
参数:
X: 数据集,形状为(n_samples, n_features)
k: 聚类簇数
random_state: 随机种子
"""
# 获取数据维度
n_dim = X.shape[1]
if n_dim > 3:
print("错误: 仅支持2D和3D数据可视化")
return
# 设置随机种子
np.random.seed(random_state)
# 创建两个KMeans模型
km_random = KMeansClusterer(n_clusters=k, init_method='random', random_state=random_state, verbose=False)
km_pp = KMeansClusterer(n_clusters=k, init_method='k-means++', random_state=random_state, verbose=False)
# 训练模型
km_random.fit(X)
km_pp.fit(X)
# 计算最终结果
print(f"{'初始化方法':<12} {'迭代次数':<12} {'最终SSE':<15} {'时间(秒)':<12}")
print("-" * 55)
print(
f"{'随机初始化':<12} {km_random.n_iter:<12d} {km_random.inertia:<15.4f} {len(km_random.history) * 0.1:<12.4f}")
print(f"{'K-means++':<12} {km_pp.n_iter:<12d} {km_pp.inertia:<15.4f} {len(km_pp.history) * 0.1:<12.4f}")
if n_dim <= 2: # 2D可视化 - 使用Matplotlib
# 创建画布
fig = plt.figure(figsize=(15, 10))
# 创建子图
# 上排: 迭代过程中的质心轨迹
ax_random_path = fig.add_subplot(231)
ax_pp_path = fig.add_subplot(232)
ax_path_compare = fig.add_subplot(233)
# 下排: 最终聚类结果和SSE对比
ax_random = fig.add_subplot(234)
ax_pp = fig.add_subplot(235)
ax_sse = fig.add_subplot(236)
# 颜色和标记
colors = ['#4EACC5', '#FF9C34', '#4E9A06', '#9A4EAE', '#C53434', '#34C5FF']
markers = ['o', '^', 's', 'd', 'p', '*']
# 绘制SSE对比曲线
ax_sse.plot(km_random.sse_history, 'r-o', linewidth=2, alpha=0.7, label='随机初始化')
ax_sse.plot(km_pp.sse_history, 'b-^', linewidth=2, alpha=0.7, label='K-means++初始化')
ax_sse.set_xlabel('迭代次数')
ax_sse.set_ylabel('SSE')
ax_sse.set_title('收敛速度对比')
ax_sse.legend()
ax_sse.grid(True, linestyle='--', alpha=0.7)
# 绘制质心轨迹
for i in range(k):
# 随机初始化的轨迹
points = np.array([h['centroids'][i] for h in km_random.history])
ax_random_path.plot(points[:, 0], points[:, 1], 'o-', c=colors[i], alpha=0.7, linewidth=1.5)
ax_random_path.scatter(points[-1, 0], points[-1, 1], s=100, c=colors[i], marker='X')
# K-means++初始化的轨迹
points_pp = np.array([h['centroids'][i] for h in km_pp.history])
ax_pp_path.plot(points_pp[:, 0], points_pp[:, 1], 'o-', c=colors[i], alpha=0.7, linewidth=1.5)
ax_pp_path.scatter(points_pp[-1, 0], points_pp[-1, 1], s=100, c=colors[i], marker='X')
# 轨迹对比
ax_path_compare.plot(points[:, 0], points[:, 1], 'r--', alpha=0.5, linewidth=1)
ax_path_compare.plot(points_pp[:, 0], points_pp[:, 1], 'b-', alpha=0.5, linewidth=1)
ax_path_compare.scatter(points[0, 0], points[0, 1], s=80, c='r', marker='o',
label='随机初始' if i == 0 else "")
ax_path_compare.scatter(points_pp[0, 0], points_pp[0, 1], s=80, c='b', marker='^',
label='K-means++初始' if i == 0 else "")
# 设置轨迹图的标题
ax_random_path.set_title('随机初始化质心轨迹')
ax_pp_path.set_title('K-means++初始化质心轨迹')
ax_path_compare.set_title('质心轨迹对比')
ax_path_compare.legend()
# 绘制数据点
for i in range(k):
# 随机初始化的结果
ax_random.scatter(
X[km_random.labels == i, 0],
X[km_random.labels == i, 1] if n_dim == 2 else np.zeros(np.sum(km_random.labels == i)),
s=30, c=colors[i], marker=markers[i], alpha=0.7,
label=f'簇{i + 1}' if i < k else None
)
# K-means++初始化的结果
ax_pp.scatter(
X[km_pp.labels == i, 0],
X[km_pp.labels == i, 1] if n_dim == 2 else np.zeros(np.sum(km_pp.labels == i)),
s=30, c=colors[i], marker=markers[i], alpha=0.7,
label=f'簇{i + 1}' if i < k else None
)
# 绘制最终质心
ax_random.scatter(km_random.centroids[:, 0], km_random.centroids[:, 1], s=150, c='black', marker='X',
label='质心')
ax_pp.scatter(km_pp.centroids[:, 0], km_pp.centroids[:, 1], s=150, c='black', marker='X', label='质心')
# 设置最终结果图的标题
ax_random.set_title(f'随机初始化结果 (迭代{km_random.n_iter}次, SSE={km_random.inertia:.4f})')
ax_pp.set_title(f'K-means++初始化结果 (迭代{km_pp.n_iter}次, SSE={km_pp.inertia:.4f})')
# 添加图例
ax_random.legend()
ax_pp.legend()
# 添加网格线
ax_random.grid(True, linestyle='--', alpha=0.7)
ax_pp.grid(True, linestyle='--', alpha=0.7)
ax_random_path.grid(True, linestyle='--', alpha=0.7)
ax_pp_path.grid(True, linestyle='--', alpha=0.7)
ax_path_compare.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()
plt.draw() # 确保绘图正常
plt.show()
elif n_dim == 3: # 3D可视化 - 使用Plotly
# 使用Plotly创建两个并排比较的3D图和一个SSE对比图
# 创建子图布局
fig = make_subplots(
rows=2, cols=2,
specs=[[{'type': 'scene'}, {'type': 'scene'}], [{'colspan': 2, 'type': 'xy'}]],
subplot_titles=(
f'随机初始化结果 (迭代{km_random.n_iter}次, SSE={km_random.inertia:.4f})',
f'K-means++初始化结果 (迭代{km_pp.n_iter}次, SSE={km_pp.inertia:.4f})',
'收敛速度对比'
),
column_widths=[0.5, 0.5],
row_heights=[0.7, 0.3],
vertical_spacing=0.05
)
# 颜色列表
colors = ['#4EACC5', '#FF9C34', '#4E9A06', '#9A4EAE', '#C53434', '#34C5FF']
# 随机初始化结果
for i in range(k):
mask = km_random.labels == i
if np.any(mask):
fig.add_trace(
go.Scatter3d(
x=X[mask, 0],
y=X[mask, 1],
z=X[mask, 2],
mode='markers',
marker=dict(
size=5,
color=colors[i % len(colors)],
opacity=0.7
),
name=f'簇{i + 1} (随机)'
),
row=1, col=1
)
# 随机初始化的质心
fig.add_trace(
go.Scatter3d(
x=km_random.centroids[:, 0],
y=km_random.centroids[:, 1],
z=km_random.centroids[:, 2],
mode='markers',
marker=dict(
size=10,
color='black',
symbol='x',
line=dict(width=2, color='black')
),
name='质心 (随机)'
),
row=1, col=1
)
# K-means++初始化结果
for i in range(k):
mask = km_pp.labels == i
if np.any(mask):
fig.add_trace(
go.Scatter3d(
x=X[mask, 0],
y=X[mask, 1],
z=X[mask, 2],
mode='markers',
marker=dict(
size=5,
color=colors[i % len(colors)],
opacity=0.7
),
name=f'簇{i + 1} (K-means++)'
),
row=1, col=2
)
# K-means++初始化的质心
fig.add_trace(
go.Scatter3d(
x=km_pp.centroids[:, 0],
y=km_pp.centroids[:, 1],
z=km_pp.centroids[:, 2],
mode='markers',
marker=dict(
size=10,
color='black',
symbol='x',
line=dict(width=2, color='black')
),
name='质心 (K-means++)'
),
row=1, col=2
)
# SSE曲线对比
fig.add_trace(
go.Scatter(
x=list(range(1, len(km_random.sse_history) + 1)),
y=km_random.sse_history,
mode='lines+markers',
name='随机初始化 SSE',
line=dict(color='red', width=2),
marker=dict(color='red', size=8)
),
row=2, col=1
)
fig.add_trace(
go.Scatter(
x=list(range(1, len(km_pp.sse_history) + 1)),
y=km_pp.sse_history,
mode='lines+markers',
name='K-means++ SSE',
line=dict(color='blue', width=2),
marker=dict(color='blue', size=8)
),
row=2, col=1
)
# 更新布局
fig.update_layout(
height=900,
width=1200,
scene=dict(
xaxis_title='特征1',
yaxis_title='特征2',
zaxis_title='特征3'
),
scene2=dict(
xaxis_title='特征1',
yaxis_title='特征2',
zaxis_title='特征3'
),
xaxis=dict(title='迭代次数'),
yaxis=dict(title='簇内平方和 (SSE)'),
title_text="随机初始化 vs. K-means++初始化对比"
)
# 显示图表
fig.show()
else:
print("错误: 仅支持2D和3D数据可视化")
return
def visualize_cluster_errors(X, kmeans):
"""
可视化聚类结果中每个簇的误差分布
参数:
X: 数据集,形状为(n_samples, n_features)
kmeans: 已训练的KMeansClusterer对象
"""
# 确保模型已训练
if kmeans.centroids is None:
print("错误: 模型未训练")
return
# 获取数据维度
n_dim = X.shape[1]
# 计算每个点到其质心的距离
labels = kmeans.labels
centroids = kmeans.centroids
distances = np.zeros(len(X))
for i in range(kmeans.n_clusters):
cluster_points = X[labels == i]
if len(cluster_points) > 0:
dist = cdist(cluster_points, centroids[i].reshape(1, -1))
distances[labels == i] = dist.flatten()
if n_dim <= 2: # 2D可视化 - 使用Matplotlib
# 创建图形
fig = plt.figure(figsize=(15, 8))
# 配置布局: 左侧数据可视化,右侧误差分布
ax_data = fig.add_subplot(121)
ax_hist = fig.add_subplot(222) # 右上: 直方图
ax_box = fig.add_subplot(224) # 右下: 簇内误差箱线图
# 颜色和标记
colors = ['#4EACC5', '#FF9C34', '#4E9A06', '#9A4EAE', '#C53434', '#34C5FF']
markers = ['o', '^', 's', 'd', 'p', '*']
# 左侧: 数据可视化,点的大小反映误差
max_distance = np.max(distances)
size_scale = 50 # 基础大小
for i in range(kmeans.n_clusters):
cluster_points = X[labels == i]
cluster_distances = distances[labels == i]
ax_data.scatter(
cluster_points[:, 0],
cluster_points[:, 1] if n_dim == 2 else np.zeros(len(cluster_points)),
s=size_scale + 100 * cluster_distances / max_distance, # 误差越大,点越大
c=colors[i % len(colors)],
marker=markers[i % len(markers)],
alpha=0.6,
edgecolors='w',
linewidths=0.5,
label=f'簇 {i + 1}'
)
ax_data.scatter(
centroids[:, 0],
centroids[:, 1] if n_dim > 1 else np.zeros(len(centroids)),
s=200,
c='black',
marker='X',
label='质心'
)
# 右上: 误差直方图
ax_hist.hist(distances, bins=30, alpha=0.7, color='skyblue', edgecolor='black')
ax_hist.set_xlabel('到质心的距离')
ax_hist.set_ylabel('样本数')
ax_hist.set_title('误差分布直方图')
ax_hist.grid(True, linestyle='--', alpha=0.7)
# 右下: 簇内误差箱线图
cluster_errors = []
cluster_labels = []
for i in range(kmeans.n_clusters):
if np.any(labels == i):
cluster_errors.append(distances[labels == i])
cluster_labels.append(f'簇 {i + 1}')
ax_box.boxplot(cluster_errors, labels=cluster_labels)
ax_box.set_ylabel('到质心的距离')
ax_box.set_title('各簇内误差分布箱线图')
ax_box.grid(True, linestyle='--', alpha=0.7)
# 数据图标题和图例
ax_data.set_title('聚类结果(点大小表示误差)')
ax_data.legend()
ax_data.grid(True, linestyle='--', alpha=0.7)
# 调整布局
plt.tight_layout()
plt.draw() # 确保绘图正常
plt.show()
elif n_dim == 3: # 3D可视化 - 使用Plotly
# 创建Plotly子图布局
fig = make_subplots(
rows=2, cols=2,
specs=[[{'type': 'scene', 'rowspan': 2}, {'type': 'xy'}],
[None, {'type': 'xy'}]],
subplot_titles=(
'聚类结果(点大小表示误差)',
'误差分布直方图',
'各簇内误差分布箱线图'
),
column_widths=[0.6, 0.4],
row_heights=[0.5, 0.5]
)
# 颜色列表
colors = ['#4EACC5', '#FF9C34', '#4E9A06', '#9A4EAE', '#C53434', '#34C5FF']
# 左侧: 3D数据可视化,点的大小反映误差
max_distance = np.max(distances)
# 添加簇中的点
for i in range(kmeans.n_clusters):
mask = labels == i
cluster_points = X[mask]
cluster_distances = distances[mask]
if len(cluster_points) > 0:
fig.add_trace(
go.Scatter3d(
x=cluster_points[:, 0],
y=cluster_points[:, 1],
z=cluster_points[:, 2],
mode='markers',
marker=dict(
size=5 + 15 * cluster_distances / max_distance, # 误差越大,点越大
color=colors[i % len(colors)],
opacity=0.7,
symbol='circle',
line=dict(width=0.5, color='white')
),
name=f'簇 {i + 1}'
),
row=1, col=1
)
# 添加质心
fig.add_trace(
go.Scatter3d(
x=centroids[:, 0],
y=centroids[:, 1],
z=centroids[:, 2],
mode='markers',
marker=dict(
size=10,
color='black',
symbol='x',
line=dict(width=2, color='black')
),
name='质心'
),
row=1, col=1
)
# 右上: 误差直方图
fig.add_trace(
go.Histogram(
x=distances,
nbinsx=30,
marker_color='skyblue',
marker_line=dict(color='black', width=1),
opacity=0.7,
name='误差分布'
),
row=1, col=2
)
# 右下: 簇内误差箱线图
cluster_errors = []
cluster_labels = []
for i in range(kmeans.n_clusters):
if np.any(labels == i):
cluster_errors.append(distances[labels == i])
cluster_labels.append(f'簇 {i + 1}')
fig.add_trace(
go.Box(
y=cluster_errors[0] if cluster_errors else [],
name=cluster_labels[0] if cluster_labels else '',
marker_color=colors[0 % len(colors)]
),
row=2, col=2
)
for i in range(1, len(cluster_errors)):
fig.add_trace(
go.Box(
y=cluster_errors[i],
name=cluster_labels[i],
marker_color=colors[i % len(colors)]
),
row=2, col=2
)
# 更新布局
fig.update_layout(
height=800,
scene=dict(
xaxis_title='特征1',
yaxis_title='特征2',
zaxis_title='特征3'
),
xaxis=dict(title='到质心的距离'),
yaxis=dict(title='样本数'),
xaxis2=dict(title='簇'),
yaxis2=dict(title='到质心的距离'),
title_text='聚类误差分析',
showlegend=True,
legend=dict(
orientation="h",
yanchor="bottom",
y=1.02,
xanchor="right",
x=1
)
)
# 显示图表
fig.show()
else:
print("错误: 仅支持2D和3D数据可视化")
return
# ==============================
# 主程序
# ==============================
def main():
"""
K均值聚类演示主程序
"""
print("=" * 50)
print("K均值聚类算法可视化演示")
print("=" * 50)
# --- 1. 数据准备 ---
print("\n1. 数据准备")
print("-" * 30)
# 生成2D数据并保存
X_2d, y_2d = generate_custom_clusters()
save_to_csv(X_2d, 'kmeans_data.csv')
# 从文件加载数据
dataset = load_from_csv('kmeans_data.csv')
# --- 2. 基本聚类和可视化 ---
print("\n2. 基本K均值聚类")
print("-" * 30)
# 使用随机初始化方法
print("\n使用随机初始化:")
kmeans_random = KMeansClusterer(n_clusters=4, init_method='random', random_state=42)
kmeans_random.fit(dataset)
# 可视化聚类结果
print("\n基本聚类结果可视化:")
show_cluster(dataset, kmeans_random.labels, kmeans_random.centroids,
title="K均值聚类结果 (随机初始化)")
# --- 3. 使用K-means++初始化 ---
print("\n3. 使用K-means++初始化")
print("-" * 30)
kmeans_pp = KMeansClusterer(n_clusters=4, init_method='k-means++', random_state=42)
kmeans_pp.fit(dataset)
# 可视化聚类结果
show_cluster(dataset, kmeans_pp.labels, kmeans_pp.centroids,
title="K均值聚类结果 (K-means++初始化)")
# --- 4. 高级可视化 ---
print("\n4. 高级可视化功能演示")
print("-" * 30)
# 4.1 随机初始化与K-means++初始化对比
print("\n4.1 初始化方法对比可视化:")
visualize_initialization_comparison(dataset, k=4)
# 4.2 聚类过程动态可视化
print("\n4.2 聚类过程动态可视化:")
visualize_kmeans_animation(dataset, kmeans_pp, interval=1000) # 增加了间隔时间,便于观察
# 4.3 簇内误差分布可视化
print("\n4.3 簇内误差分布可视化:")
visualize_cluster_errors(dataset, kmeans_pp)
# --- 5. 3D数据示例 ---
print("\n5. 3D数据聚类演示")
print("-" * 30)
# 生成3D数据
X_3d, y_3d = generate_cluster_data(n_samples=500, n_features=3, centers=4, cluster_std=0.8)
# 3D聚类
print("\n3D数据聚类:")
kmeans_3d = KMeansClusterer(n_clusters=4, init_method='k-means++', random_state=42)
kmeans_3d.fit(X_3d)
# 可视化3D聚类结果
print("\n3D聚类结果可视化:")
show_cluster(X_3d, kmeans_3d.labels, kmeans_3d.centroids, title="3D K均值聚类结果")
# 3D数据聚类过程动态可视化
print("\n3D聚类过程动态可视化:")
visualize_kmeans_animation(X_3d, kmeans_3d, interval=1000)
print("\n演示完成!")
if __name__ == "__main__":
# 运行主程序
main()
"随机生成k均值聚类数据集.py"的程序运行结果如下:
![]()

![]()



kmeans_data.csv


"k均值聚类.py"的程序运行结果如下:
==================================================
K均值聚类算法可视化演示
==================================================
1. 数据准备
------------------------------
生成数据集: 500个样本, 2维特征, 4个簇...
数据已保存至: kmeans_data.csv
成功加载数据集: kmeans_data.csv, 大小: 500
2. 基本K均值聚类
------------------------------
使用随机初始化:
使用随机方法初始化聚类中心...
迭代 1: SSE = 4245.1649, 质心移动距离 = 8.867450
迭代 2: SSE = 635.2410, 质心移动距离 = 3.043416
迭代 3: SSE = 607.9868, 质心移动距离 = 0.052485
迭代 4: SSE = 607.9868, 质心移动距离 = 0.000000
算法在第4次迭代后收敛
K均值聚类完成,用时 0.0011 秒
总迭代次数: 4, 最终SSE: 607.9868
基本聚类结果可视化:

3. 使用K-means++初始化
------------------------------
使用K-means++初始化聚类中心...
迭代 1: SSE = 647.2863, 质心移动距离 = 2.977551
迭代 2: SSE = 607.9868, 质心移动距离 = 0.085365
迭代 3: SSE = 607.9868, 质心移动距离 = 0.000000
算法在第3次迭代后收敛
K均值聚类完成,用时 0.0025 秒
总迭代次数: 3, 最终SSE: 607.9868

4. 高级可视化功能演示
------------------------------
4.1 初始化方法对比可视化:
初始化方法 迭代次数 最终SSE 时间(秒)
-------------------------------------------------------
随机初始化 4 607.9868 0.4000
K-means++ 2 607.9868 0.2000

4.2 聚类过程动态可视化:

4.3 簇内误差分布可视化:

5. 3D数据聚类演示
------------------------------
生成数据集: 500个样本, 3维特征, 4个簇...
3D数据聚类:
使用K-means++初始化聚类中心...
迭代 1: SSE = 924.0294, 质心移动距离 = 2.636694
迭代 2: SSE = 924.0294, 质心移动距离 = 0.000000
算法在第2次迭代后收敛
K均值聚类完成,用时 0.0010 秒
总迭代次数: 2, 最终SSE: 924.0294
3D聚类结果可视化:
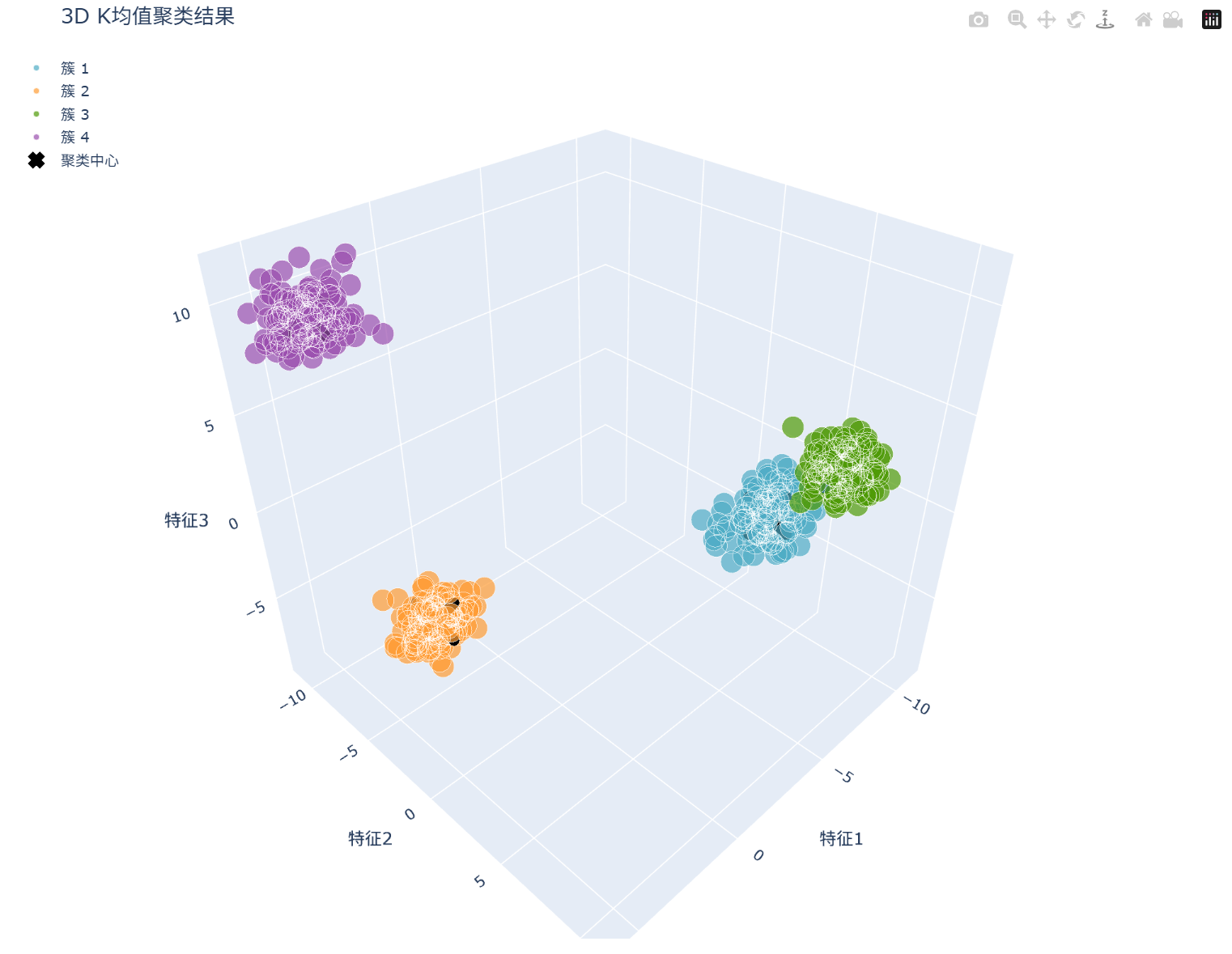
3D聚类过程动态可视化:

演示完成!
五、总结
k均值聚类(k-Means Clustering)是一种无监督学习的分类算法,旨在将数据点划分为k个不同的簇,使得每个数据点属于离它最近的质心(簇中心)所代表的簇。该算法迭代进行,直到满足收敛条件。
k均值聚类作为一种经典算法,凭借其简单高效的特性,在各领域中展现出强大的应用价值。尽管存在一些局限性,但通过适当的预处理、参数选择和算法改进,k均值聚类仍能有效地应对各种实际问题。随着计算技术的发展和算法的不断完善,k均值聚类及其变体将在更多场景中发挥重要作用,为数据分析和决策提供有力支持。
在实际应用中,k均值聚类通常不是独立使用的,而是作为数据分析流程中的一个环节,与其他技术相结合,共同构建完整的解决方案。因此,深入理解k均值聚类的原理、特性和应用场景,对于充分发挥其价值至关重要。





















 286
286

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








