万字长文！一文了解归一化：从Transformer归一化到主流大模型归一化的演变！

引言

自Transformer架构被提出来之后，人们一直都在对Transformer架构进行更改，例如：从正余弦位置编码旋转位置编码RoFE、从多头Attention到DeepSeek的MLA、从前馈神经网络到当前的MoE架构等。

而归一化（Normalization）在整体Transformer架构中并没有做太多的改进，但它对模型能否顺利训练，却有着很关键的作用。本文将带你一文了解归一化（Normalization），包括其背景、种类、Transformer归一化及源码、大模型常见归一化、大模型归一化位置等。文章安排如下：

归一化的作用

归一化（Normalization）又叫正则化、规范化、标准化等，它是一种数据处理方式，「能将数据经过处理后限制在某个固定范围内」，来方便后面神经网络对数据的处理。它是神经网络不可以或缺的一环。正常使用的话，现在基本只需几行代码就能实现，但要用得好，还是需要了解它。下面将介绍归一化的主要作用：

1、数据可比性

那么为什么要把数据限制到某个固定的范围呢？目标解决数据间的可比性。这里其实有一个从量纲和无量纲的概念。

举个例子：当我们在做对房价的预测时，收集到的数据中，如房屋的面积、房间的数量、到地铁站的距离等，这些都是量纲，其对应的量纲单位分别为平方米、个数、米等。「这些量纲单位的不同，导致数据之间不具有可比性」。同时，对于不同的量纲，数据的数量级大小也是不同的，比如房屋到地铁站的距离可以是上千米，而房屋的房间数量一般只有几个。经过归一化处理后，「不仅可以消除量纲的影响，也可将各数据归一化至同一量级，从而解决数据间的可比性问题」。

2、提高最优求解速度

按照上面给出的例子，假设通过房子到地铁站的距离、房间数量这两个变量来预测房价。那么预测公式和损失函数分别为：

「在未归一化时」，房子到地铁站的距离的取值在0～5000之间，而房间个数的取值范围仅为0～10。假设，，那么损失函数的公式可以写为：

可将该损失函数寻求最优解过程可视化为下图：图1：损失函数的等高线，图1（左）为未归一化时，图1（右）为归一化:图1中，左图的红色椭圆代表归一化前的损失函数等高线，蓝色线段代表梯度的更新，箭头的方向代表梯度更新的方向。「寻求最优解的过程就是梯度更新的过程，其更新方向与等高线垂直」。

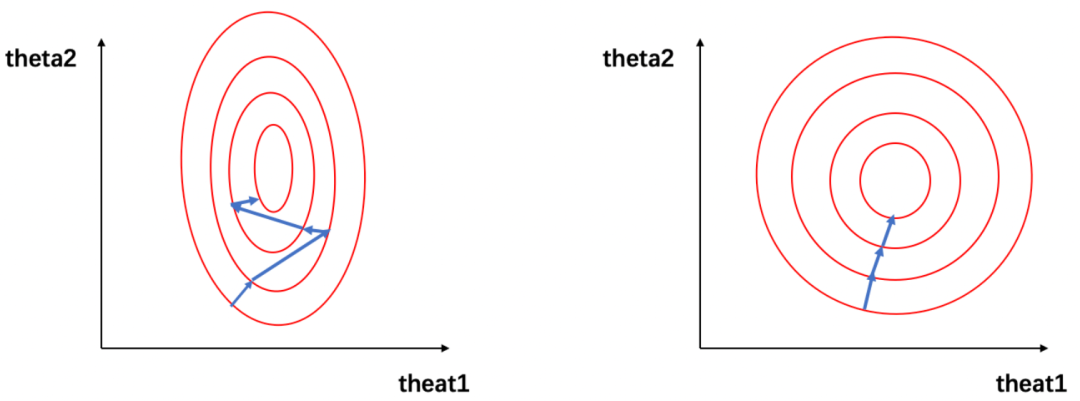
由于和的量级相差过大，损失函数的等高线呈现为一个瘦窄的椭圆。因此如图1（左）所示，瘦窄的椭圆形会使得梯度下降过程呈之字形呈现，导致梯度下降速度缓慢。

「当数据经过归一化后」，, 那么损失函数的公式可以写为：

可以看到，经过归一化后的数据属于同一量级，损失函数的等高线呈现为一个矮胖的椭圆形（如图1（右）所示），「求解最优解过程变得更加迅速且平缓，因此可以在通过梯度下降进行求解时获得更快的收敛」。

3、远离激活函数饱和区

神经网络中还有一个重要组件，非线性激活函数，比如常用的sigmoid。

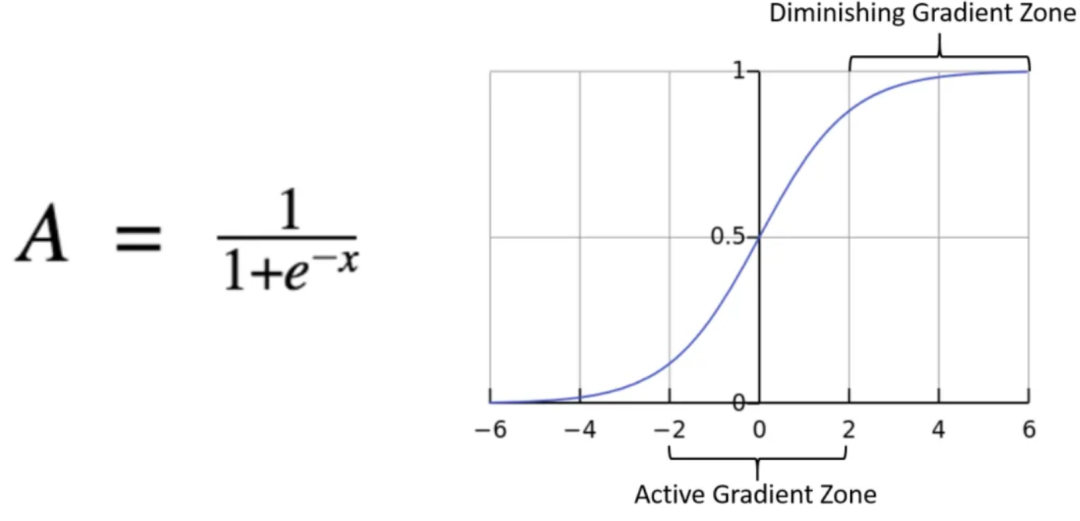
比如，上图当输入 > 6 或者 < -6 的时候，sigmoid函数的梯度已经变得非常小，也就是进入了饱和区。这种情况下训练就变得困难。

在没有normalization的情况下，分布不断变化，后面层的参数变化激烈，导致输出值更容易进入到左右两端，更容易进入到激活函数的饱和区。「而归一化能把部分输出值拉回到梯度正常的范围内，一定程度缓解了梯度消失的问题，使训练可以正常进行下去」。

4、缓解ICS

机器学习里有一个叫独立同分布（i.i.d）的假设。它指的是每次抽样之间相互独立，并且「每次抽样都服从相同的分布」。这一假设对于机器学习至关重要，因为它确保了训练数据能够代表整体数据分布，从而使模型能够从历史数据中学习并对未来数据做出准确预测。

i.i.d.假设简化了模型学习过程，使得模型训练更快速、更容易。然而，并非所有机器学习场景都严格遵循i.i.d.假设。在多层神经网络中，由于上层参数的变化导致下层输入分布的变化，这违反了i.i.d.假设，从而影响了模型的学习效果和训练难度，这种现象被称为内部协变量偏移（ICS）。

「为了解决ICS问题，一种可能的方法是采用归一化技术，如Batch Normalization，通过将上一层的输出映射到一个固定的分布上，来稳定下一层的输入分布，从而降低学习难度」。尽管有研究表明Batch Normalization的作用机制与ICS的关系可能并不大，指出ICS问题也可以通过改变初始化策略、调整训练超参数（如学习率）等方法来优化，但相比归一化方法，此类方法的效率并不是很高。

归一化类型

常见的归一化类型可以分为线性归一化和非线性归一化，其中线性归一化包含：Min-max归一化、mean归一化、Z-score归一化等；非线性归一化包含：对数归一化、反正切归一化、小数对标标准化。以下是详细介绍：

线性归一化

「Min-max normalization」（最小-最大归一化）是一种常用的数据预处理技术，它将数据缩放到一个固定的范围，通常是[0, 1]，这有助于改善算法的性能，尤其是在涉及距离计算的算法中，如K-最近邻（KNN）、K-均值聚类等。

由于直接使用了数据的最大值和最小值，Min-max normalization「对异常值非常敏感」。如果数据集中包含异常值，这些值可能会极大地影响归一化的结果。计算公式如下：

「Z-score normalization」（标准化）是数据预处理中常用的一种方法，它通过计算每个数据点与均值之间的差异，并将其除以标准差，「来将原始数据转换为具有零均值和单位方差的新数据集」。这种方法使数据符合标准正态分布，具有均值为0和标准差为1的特性。「在数据存在异常值、最大最小值不固定的情况下，可以使用标准化」。计算公式如下：

其中：是原始数据点。μ 是原始数据集的均值。σ是原始数据集的标准差。是归一化后的数据点。

「Mean normalization」，均值归一化通过减去数据的均值并除以数据的最大值和最小值之差来调整数据的尺度，数据被缩放到一个特定的范围内，通常是[0, 1]。这种方法的目标是使数据在特征空间中具有统一的尺度，从而有助于提高机器学习模型的性能和收敛速度。

但是「数据中不应包含大量的异常值」，因为这些值可能会对最大值和最小值产生较大影响，从而影响归一化的效果。计算公式如下：

非线性归一化

「No-line normalization」 非线性归一化，常见的有对数归一化、反正切函数归一化、小数定标标准化。它们通常被用「在数据分化程度较大的场景」，有时需要通过一些数学函数对原始值进行映射，如对数、反正切等。

「对数归一化」通过取数据的对数来降低数据的动态范围，从而将数据压缩到一个较小的区间内。这种方法对于具有指数增长或极端值的数据特别有用。公式如下：

「反正切函数归一化」使用反正切函数（arctan）来将数据映射到 [-1, 1] 的范围内。这种方法对于处理具有极端值或非线性分布的数据特别有效，因为它可以减少极端值的影响。同时，可以保留数据的相对差异，并且将数据限制在一个固定的范围内。公式如下：

「小数定标标准化」（Decimal Point Normalization）：通过移动数据的小数点位置来实现归一化。这种方法适用于数据范围较大且数据值相对稳定的情况。归一化后的数据范围为 ([-1, 1])，为使的最小整数。公式为：

归一化使用总结

1、「Min-max归一化和mean归一化适合在最大最小值明确不变的情况下使用」，比如图像处理时，灰度值限定在 [0, 255] 的范围内，就可以用min-max归一化将其处理到[0, 1]之间。在最大最小值不明确时，每当有新数据加入，都可能会改变最大或最小值，导致归一化结果不稳定，后续使用效果也不稳定。

同时，数据需要相对稳定，如果有过大或过小的异常值存在，min-max归一化和mean归一化的效果也不会很好。如果对处理后的数据范围有严格要求，也应使用min-max归一化或mean归一化。

2、Z-score归一化也可称为「标准化」，经过处理的数据呈均值为0，标准差为1的分布。「在数据存在异常值、最大最小值不固定的情况下，可以使用标准化」。标准化会改变数据的状态分布，但不会改变分布的种类。特别地，神经网络中经常会使用到z-score归一化，针对这一点，我们将在后续的文章中进行详细的介绍。

3、非线性归一化通常被用「在数据分化程度较大的场景」，有时需要通过一些数学函数对原始值进行映射，如对数、反正切等。

归一化和标准化关系

上面既有归一化也有标准化，那么两者之间有什么关系呢？

谈到归一化和标准化可能会存在一些概念的混淆，我们都知道「归一化是指normalization，标准化是指standardization」，但根据wiki上对feature scaling方法的定义，standardization其实就是z-score normalization，也就是说标准化其实是归一化的一种，而一般情况下，我们会把z-score归一化称为标准化，把min-max归一化简称为归一化。在下文中，我们也是用「标准化指代z-score归一化」，并使用「归一化指代min-max归一化」。【有点绕】

其实，「归一化和标准化在本质上都是一种线性变换」。在4.归一化类型中，我们提到了归一化和标准化的公式，对于归一化的公式，在数据给定的情况下，可以令、，则归一化的公式可变形为：

标准化的公式与变形后的归一化类似，其中的和在数据给定的情况下，可以看作常数。因此，标准化的变形与归一化的类似，都可看作对按比例进行缩放，再进行个单位的平移。由此可见，归一化和标准化的本质都是一种线性变换，他们都不会因为对数据的处理而改变数据的原始数值排序。

「那么归一化和标准化又有什么区别呢？」

归一化不会改变数据的状态分布，但标准化会改变数据的状态分布；
归一化会将数据限定在一个具体的范围内，如 [0, 1]，但标准化不会，标准化只会将数据处理为均值为0，标准差为1的状态分布。

大模型归一化

前面主要介绍了一些归一化的基础知识，它能够提高模型训练的稳定性，因为此目前大模型架构中都加入归一化。如果没有进行归一化的处理，那么每一批次的训练数据的分布是不一样的，

从大的方向上来看，神经网络则需要在这多个分布当中找到平衡点，
从小的方向上来看，由于每层的网络输入数据分布在不断地变化，那么会「导致每层网络都在找平衡点，显然网络就变得难以收敛」。

常见的模型归一化方法有：批量归一化（Batch Norm，BN）、层归一化（Layer Norm，LN）、RMS Norm、Deep Norm。

批量归一化(BN)

假设输入数据的形状是，其中是batch size，是特征向量维度。

这个输入特征每个都有不同的含义，如我们前面的例子，假如：第一个元素是房子到地铁站的距离，第二个元素是房子的房间数，因此做normalization的时候这个特征分别来做。

具体来说，对于第个特征维度，首先计算整个batch内的均值

再计算这个维度上的方差

得到均值方差之后，对batch内维度上的所有值进行Z-score normalization

其中 ϵ 是为了防止分母为0。这个在实际代码中挺重要的，忘记加可能会出问题。经过这样的变换之后，在 C 个特征维度上就是均值为0，方差为1的分布了。

不过这还没完，每个维度的数值全部归一化之后，对于激活函数来说，更集中在中间的部分，而这部分的非线性特征并不强，这样非线性激活层近似了一个线性变换，这样就降低了模型的学习能力。如下图：

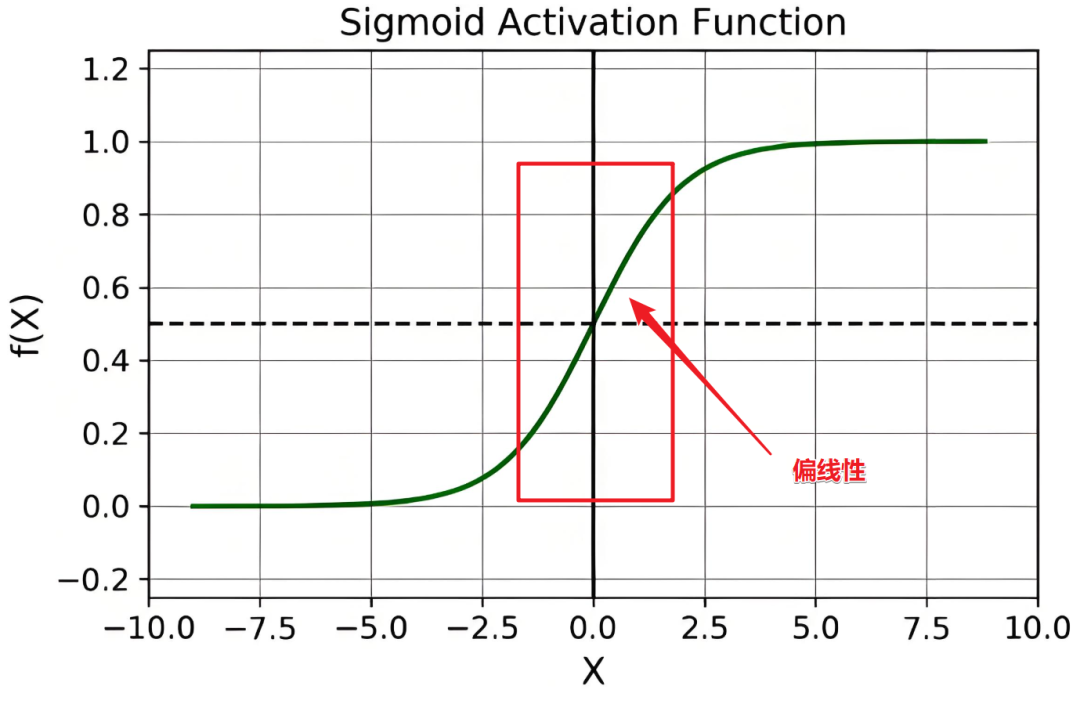
且无论输入是什么，最终输出都会被强行拉到这样一个“平均”的值，也极大抑制了模型的表达能力。「所以为了保证模型的能力，也保证非线性能力的获得，对每个特征，又增加两个可学习的参数」，缩放参数和位移参数，这两个参数都是通过模型学习得到的。

这样每个特征值就有机会从“线性区”移动到“非线性区”，把被归一化削弱的非线性能力找了回来。

并且通过这样一个归一化再重新缩放移动的操作，解耦了上层输出分布和下层输入，本来下层参数要去适应上层分布变化，现在只需要通过每个batchnorm层中的和直接学习就行了，训练变得简单了。具体算法如下：

参考：https://arxiv.org/pdf/1502.03167

批归一化（BN）通常用于卷积神经网络（CNNs），在具有大数据集和较大批大小的情况下效果较好。

层归一化(LN)

上面介绍的批归一化在批次维度上计算统计量，其依赖于批次的大小。「而层归一化针对单个样本的特征进行归一化操作，与批归一化（Batch Normalization）不同，它沿着特征维度而非批次维度进行统计计算」。它最早由Geoffrey Hinton团队于2016年提出。它对解决深度神经网络训练中的问题具有显著效果。

对于一个输入张量，层归一化计算每个样本内所有特征的均值和方差，然后用这些统计量对特征进行归一化。其最主要的应用就是NLP的模型，包括RNN、Transfomrer模型，当然也包括当前的大模型架构。

下面是BN和LN的对比图：

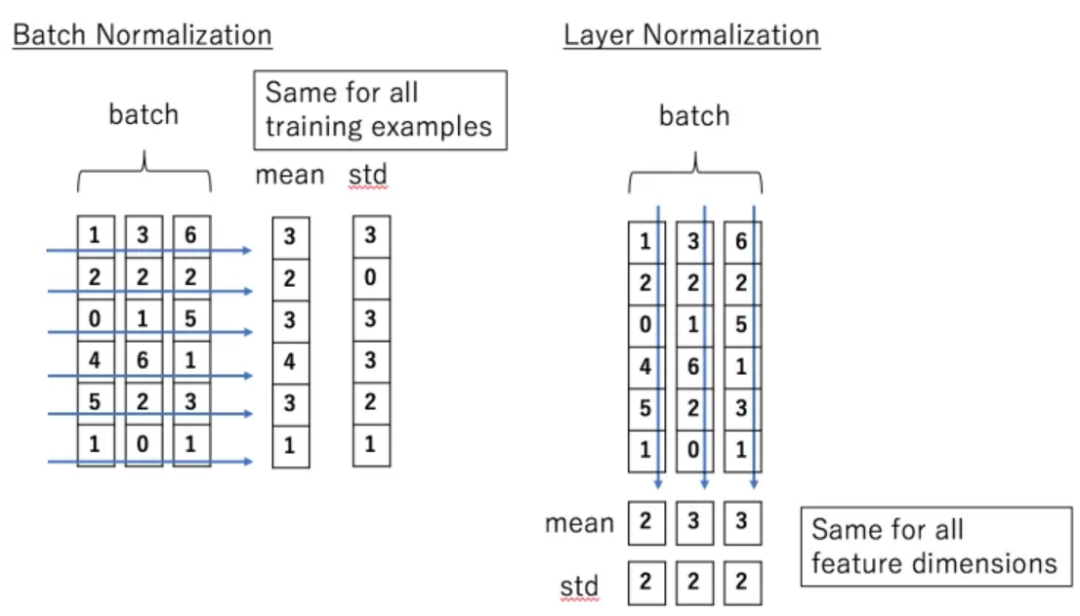
相比BN归一化，LN归一化的维度似乎解释性没那么强。BN是对同一个特征，比如计算房子距离地铁站的距离均值是有意义的，而layernorm在不同的特征，比如房子距离地铁站的距离、房子房间个数等，好像并没有可靠的物理意义。

「其具体的计算过程如下：」

对于输入（B为批次大小，D为特征维度），层归一化的计算步骤如下：

计算每个样本的均值：
计算每个样本的方差：
归一化：
缩放和平移：

其中和是可学习的缩放和偏移参数，是一个小常数，用于数值稳定性。

「代码实现如下：」

import torch
import torch.nn as nn

# 手动实现层归一化
deflayer_norm_manual(x, gamma, beta, eps=1e-5):
    # x: [batch_size, feature_dim]
    mean = x.mean(dim=-1, keepdim=True)
    var = x.var(dim=-1, unbiased=False, keepdim=True)
    x_norm = (x - mean) / torch.sqrt(var + eps)
    return gamma * x_norm + beta

# 使用PyTorch内置的LayerNorm
layer_norm = nn.LayerNorm(normalized_shape=512)  # 特征维度为512
output = layer_norm(input_tensor)

BN VS. LN归一化

为什么目前大多数大模型都采用层归一化呢？下面将给出具体的解释。

在Transformer中，一般输入的形状是，是序列长度，每个样本的长度可能不同，因此在这个维度需要使用padding（一般是zero-padding）来把batch内的数据处理成一样长。比如这样一批文本输入:

我  爱  中  国
你  好
谢  谢  你

为了使模型能够统一处理，通过padding将文本变成以下内容：

我  爱  中  国
你  好  [P] [P]
谢  谢  你  [P]

可以发现，由于存在padding的存在，做BN归一下显然是不合适的，比如上面的例子，对 「[“中”，“[P]”，“你”]」 做BN归一化，由于 [P] 的存在，实际的batch size只有2，并且和 [P] 做归一下也对训练没什么帮助。而且对于文本数据，batch内同一个位置上的字是不同的，对完全没有关系的字进行归一化也并没有什么意义。

也就是说，哪怕没有 [P] 的存在，比如对第一个token 「[“我”，“你”，“谢”]」 做归一化，直觉上也不太有物理意义。因此使用LN归一化，在维度上进行归一化，同时有个γ 和β 需要学习。相当于计算每一句输入内，每个token所有特征之间的均值和方差来进行归一化。

除此之外，由于layernorm不需要再batch维度上计算均值和方差，所以不存在训练和推理的时候不一样的地方，不用保存一个全局的均值和方差供推理的时候使用。而由于LN归一化和batch无关，也就不会受到batch size大小的影响。

文章《PowerNorm: Rethinking Batch Normalization in Transformers》研究了transformer中BN为啥表现不太好。其研究结果发现BN归一化在NLP任务上（IWSLT14）batch的均值和方差一直震荡，偏离全局的running statistics，而在CV任务上震荡更小，且训练完成后，也没有离群点。

总结来说，「Transformer中BN表现不太好的原因可能在于CV和NLP数据特性的不同，对于NLP数据，前向和反向传播中，batch统计量及其梯度都不太稳定」。更重要的是，实际效果就是LN归一化在NLP任务上的效果比BN归一化好。

RMSnorm归一化

「RMSnorm是LN归一化(Layer Normalization)的变体」，其最早在论文《Root Mean Square Layer Normalization》中提出。为了提高层归一化的训练速度，RMSNorm简化了传统Layer Normalization的计算流程，移除了均值中心化步骤，只保留了均方根缩放操作。其核心思想是通过特征的均方根（RMS）值来归一化数据，减少计算量的同时保持良好的性能。

「其具体计算过程如下：」

对于输入向量，RMSNorm的计算如下：

计算均方根(RMS)：
归一化：
缩放和偏移（可选）：

其中：

是一个小常数，用于数值稳定性
是可学习的缩放参数（逐元素乘法）
是可学习的偏移参数（通常在RMSNorm中省略）

「pytorch代码实现」

import torch
import torch.nn as nn

classRMSNorm(nn.Module):
    def__init__(self, dim, eps=1e-6):
        """
        初始化RMSNorm
        
        参数:
            dim: 特征维度
            eps: 数值稳定性常数
        """
        super().__init__()
        self.scale = nn.Parameter(torch.ones(dim))
        self.eps = eps
        
    defforward(self, x):
        """
        应用RMSNorm
        
        参数:
            x: 输入张量，形状为 [..., dim]
        """
        # 计算RMS
        rms = torch.sqrt(torch.mean(x ** 2, dim=-1, keepdim=True) + self.eps)
        
        # 归一化
        x_norm = x / rms
      
        # 应用缩放参数
        return self.scale * x_norm

「RMSNorm归一化对比LN归一化」

「计算简化」：RMSNorm移除了均值中心化步骤，只关注特征的缩放
- LayerNorm:
- RMSNorm:
「计算效率」：RMSNorm计算更高效，减少了约30%的计算量
「参数使用」：标准RMSNorm通常只使用缩放参数，不使用偏移参数

使用 RMSNorm 的 Transformer 模型相比于之前使用 LayerNorm 训练的模型在训练速度和性能上均具有一定优势。成为了现代大语言模型的标准组件，例如：ChatGLM、Llama、Qwen、DeepSeek等都使用该方法进行归一化。在实践中，当模型规模增大或追求训练/推理速度时，RMSNorm往往是比Layer Normalization更优的选择。

DeepNorm归一化

DeepNorm源于微软2022年的一篇文章《DeepNet: Scaling Transformers to 1,000 Layers》。对比LN归一化，DeepNorm归一化增加了深度自适应的缩放机制。它是一种专为超深度神经网络设计的归一化技术，「主要用于解决训练极深层网络时出现的梯度消失和爆炸问题」。它是对传统归一化方法的扩展和改进，「特别适用于有数百甚至上千层的深度模型」。

DeepNorm在 LayerNorm 的基础上，在残差连接中对之前的激活值按照一定比例进行缩放，能够更好地支持层数扩展。其计算公式如下：

其中，表示 Transformer 层中的前馈神经网络或注意力模块。其中是根据模型参数定的常数。这里相比post-norm提升了恒等分支的权重，使训练更容易进行。另外，还用了一个参数，把中的参数进行了缩小，以此来稳定模型的训练。

归一化模块位置

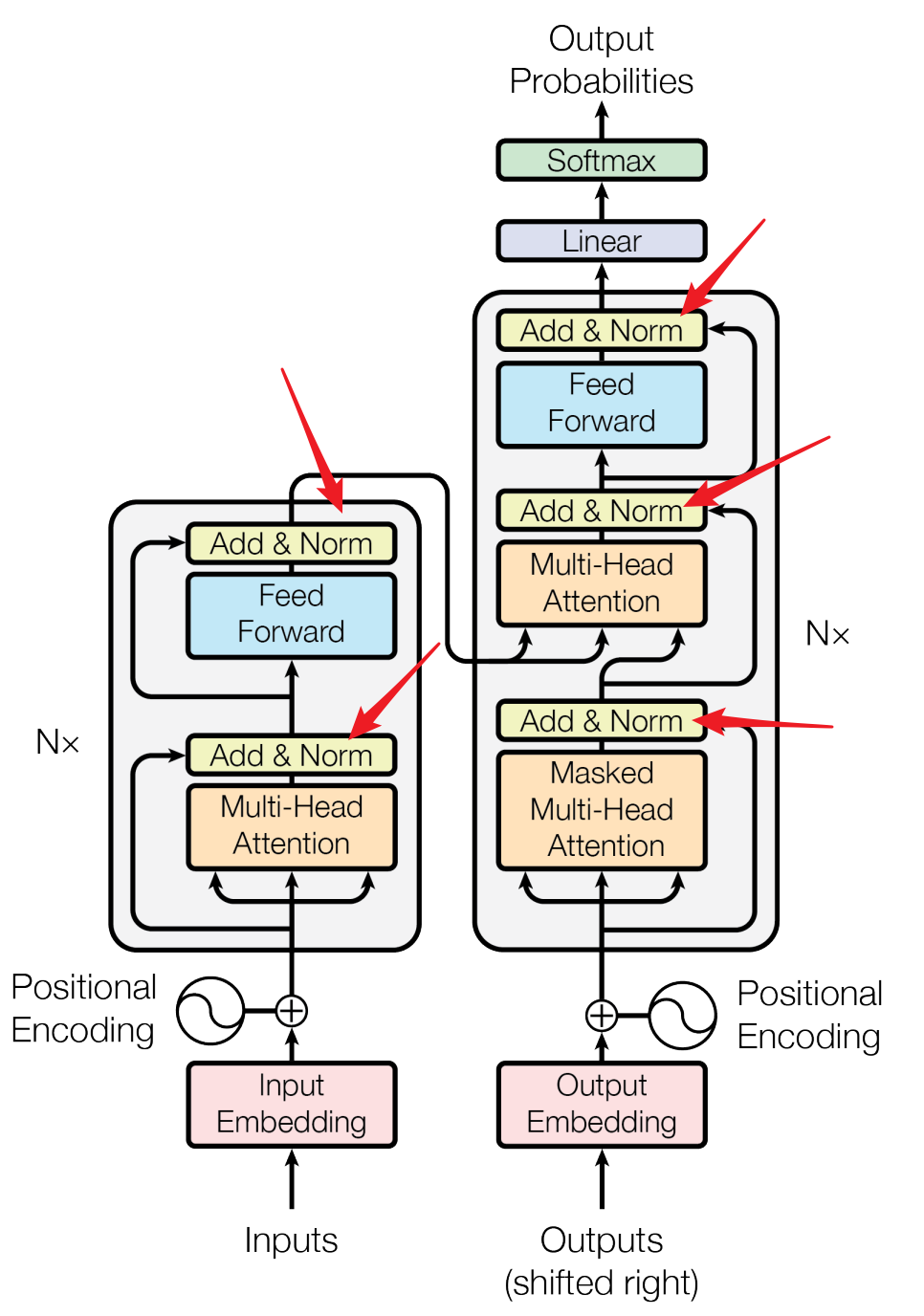
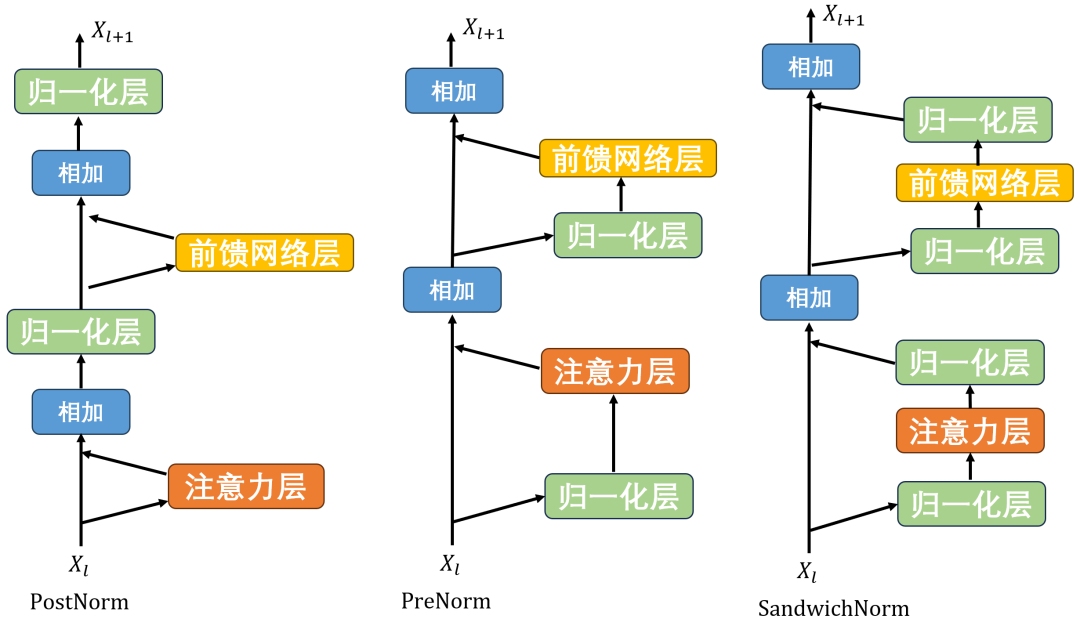
归一化模块的位置对于训练稳定性也具有重要影响。如下图所示，「归一化模块的位置通常由三种选择」，分别是层后归一化（post-layer normalization，PostNorm）、层前归一化（pre-layer normalization，PreNorm）和夹心归一化（sandwich-layer normalization，SandwichNorm）。对于最原始的Transformer架构来说，其主要是PostNorm，如上图所示。

Post-Norm

原始 Transformer 模型使用了PostNorm归一化技术，「将归一化模块放置于残差计算之后」，计算公式如下：

其中，Norm 表示任意一种归一化方法。从原理上，PostNorm 具有很多优势。首先，Post-Norm 有助于加快神经网络的训练收敛速度，防止模型出现梯度爆炸或者梯度消失的问题，从而减少训练时间。

其次，Post-Norm 可以降低神经网络对于超参数（如学习率、初始化参数等）的敏感性，使得神经网络更容易进行调优。「然而由于输出层附近的梯度可能较大，PostNorm 有时会引发训练不稳定的现象。因此，在预训练的大语言模型中，Post-Norm 很少被单独使用，通常是与其他策略相结合应用。」例如，GLM-130B 既采用了 PostNorm 和 DeepNorm。

Pre-Norm

.与 Post-Norm 不同，PreNorm「将归一化模块应用在每个子层之前」。其计算公式如下：

顾名思义，PreNorm 在每个子层前添加了一个归一化模块。由于针对每个模块输入的表示进行归一化，可以缓解梯度爆炸或者梯度消失问题。此外，PreNorm 在最后一个 Transformer 层后还额外添加了一个 LayerNorm。「相比较于 PostNorm，PreNorm 虽然在性能上略有逊色，但是在训练过程中更加稳定」。「因此，很多主流的大语言模型都采用了PreNorm」。

SandwichNorm

在 Pre-Norm 的基础上，SandwichNorm 「在残差连接之前增加了额外的 LayerNorm，主要是为了避免 Transformer 层输出出现数值爆炸的情况」。其具体的实现方式如下：

本质上，Sandwich-Norm 可以看作 Pre-Norm 和 Post-Norm 两种方法的组合，理论上具有更好的归一化效果。「但是研究人员发现，Sandwich-Norm 有时仍然无法保证大语言模型的稳定训练，甚至会引发训练崩溃的问题」。

如何学习AI大模型？

我在一线互联网企业工作十余年里，指导过不少同行后辈。帮助很多人得到了学习和成长。

我意识到有很多经验和知识值得分享给大家，也可以通过我们的能力和经验解答大家在人工智能学习中的很多困惑，所以在工作繁忙的情况下还是坚持各种整理和分享。但苦于知识传播途径有限，很多互联网行业朋友无法获得正确的资料得到学习提升，故此将并将重要的AI大模型资料包括AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频免费分享出来。