模糊综合评价

模糊综合评价法:

是一种基于模糊数学的综合评价方法，适用于处理具有模糊性和不确定性的评价问题。

比如:高与矮， 长与短，大与小，多与少，穷与富，好与差年轻与年老等。这类现象不满足“非此即彼”的排中律，而具有“亦此亦彼”的模糊性。

下面根据一下例题来讲解

究竟怎么样算是年轻人

解题步骤:

1.模糊集合与隶属函数

传统的集合理论中，元素要么属于某个集合，要么不属于某个集合，具有明确的边界。而在模糊集合中，元素对于集合的隶属关系是模糊的，用隶属度来表示元素属于集合的程度，取值范围在之间。

例如，对于 “年轻人” 这个模糊集合，一个 25 岁的人可能属于 “年轻人” 集合的隶属度为 0.8，这表示他在一定程度上属于 “年轻人”，但不是绝对属于。

隶属函数

隶属函数是用来描述元素隶属度的函数，根据具体问题可以采用不同的形式，如三角形隶属函数、梯形隶属函数、正态分布隶属函数等。

比如

在这里我们表示的意思是:当一个人小于20岁的时候我们认为他是一个年轻人,大于40岁的时候就不是年轻人了,但是20-40之间的岁数,就根据这个隶属度来确定到底算不算作年轻人,多少算是年轻人

针对这个模糊集合其实就分为大概的3类

这里我们用柯西分布来确定

我们规定25岁以下的人是年轻人,同时30岁的人的年轻人隶属度为 0.5,β是2.计算出α为0.04,得出我们自己定义的隶属函数是

(隶属函数的确定方法:F分布)

在一个荧光屏上，用以光点的上下运动快慢来代表15种不同的运动速度，记U={1,2,…, 15}.主试者随机给出15种速率，让被试者按“块”、“中”、“慢”进行判断分类，每种速率共给出320次，判断结果如下表所示

所以快是极大型,中是中间型,慢是极小型

这里使用梯形分布

对于<快>

(因为小于84就没有快的了,大于320就全是快的了

对于<中>

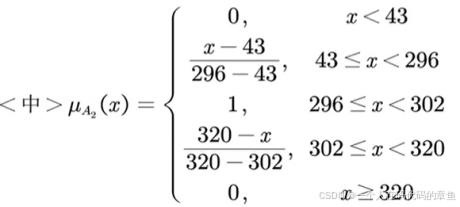
(小于43就没有中的了,因为296和302之间就只有中,所以在这个区间的我们去取1,大于320的就没有中的了)

对于<慢>

(小于41的就全是慢的了,大于320的就没有慢的了)

2.模糊评价的步骤

(1)确定评价因素集：

将影响评价对象的各种因素构成一个集合U={u1,u2,u3...un}，这些因素是评价的依据。例如，在评价一款手机时，评价因素集可以是U={外观，性能，续航，价格}。

(2)确定评价等级集：

将评价结果划分成不同的等级，构成集合V={v1,v2...vm}。例如，评价等级集可以是V={优秀，良好，中等，较差，差}。

(3)确定模糊关系矩阵R：

对每个评价因素ui，评估其在各个评价等级vj上的隶属度，形成模糊关系矩阵R。矩阵R的元素rij表示第i个评价因素属于第j个评价等级的隶属度.

这里如果是带有主观色彩的可以直接自己评价,如果是具体的数据,就可以利用隶属函数来计算对应的隶属度

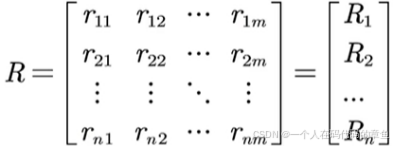
如果从行来解释,每行表示一个因素,每列表示对应的评价

如果第一行表示的是沟通的能力,那么 r11 就是沟通能力优秀的隶属,如果是1,那么就是绝u第的优秀,如果是0.6 就是相对的优秀.依次类推

(4)确定权重集A：

根据各个评价因素的重要性，赋予相应的权重A={a1,a2...an}，构成权重集A={a1,a2...an}，满足ai相加为1。权重可以通过层次分析法、专家打分法等确定。例如A={0.3,0.2,0.2,0.3}，对于手机评价因素，权重集可能是，表示 “外观” 权重为 0.2，“性能” 权重为 0.3 等。

(5)模糊综合评价：

通过模糊合成运算B=A*R，得到综合评价结果B，B是一个1*m的行向，其元素bj表示评价对象属于第j个评价等级的综合隶属度。

例子

一级模糊综合评价

我们以年终评选的例子为例;

下面的评语集合带有主观的评价色彩,采用的是打分的方式,而不是隶属函数的方式

(1)取因素集U=〈政治表现u1,工作能力u2,工作态度u3,工作成绩 u4)

(2)取评语集V={优秀v1,良好v2,一般u3,较差v4,差 v5〉。

(3)确定各因素权重A=[0.25,0.2,0.25,0.3](层次or熵权法)

(4)确定模糊综合判断矩阵,对每个因素u做出评价:

①u,由群众评议打分确定:R1=[0.1,0.5,0.4,0,0]，这个式子表示，有10%的人认为政治表现优秀50%的人认为政治表现良好，40%的人认为政治表现一般，认为政治表现较差或差的人数为0

②u2和u3由部门领导打分确定:R2=[0.2,0.5,0.2,0.1,0];R3=[0.2,0.5,0.3,0,0

③u4由单位考核组成员打分确定:R4=[0.2,0.6,0.2,0,0]

这里的每一行都表示一个因素,每一列都表示一个评价等级

下面我们以采矿方案为例子

这里是具体的数据,我们先确定隶属函数,在去确定R矩阵

某露天煤矿有五个边坡设计方案，其各项参数根据分析计算结果得到边坡设计方案的参数如下:

这里的矿物存储量8800,开发投资不超过8000w,选出最优的方案

第一步,确定模糊集合 和 隶属函数

权重集可以使用层次分析法/熵权法来确定:

根据上面的因素和 方案这两个维度计算出方案的权重

然后根据常识来确定隶属函数的类型:

采矿量越多越好    ,偏大型

基建投资越少越好  ,偏小型

采矿成本越少与好  ,偏小型

不稳定费用越小越好,偏小型

隶属函数只要符合类型和常识下的增长趋势就好

然后我们根据上面的表格,算出对应的值带入表格

上面这个就是R

计算出 B=A*R=(0.7435,0.5919,0.6789,0.3600,0.3905)

所以我们认为 方案1最好

多级模糊综合评价

上面的都是一级的模糊综合评价,他只是单一层面的,而现实中可能会是多因素的,比如说上面讲过的沟通能力,可能就可以通过业务沟通满意度,组内和谐程度等等因素反应,所以就还会有多级的模糊综合评价

多级模糊综合评价

 

上面这个就是二级模糊综合评价,因为每一个因素都对应了一套评价因素

这里的各个因素内部的更小一级的评价因素互不干扰

解题步骤

1,划分因素集

,确定评价集

2,使用模糊综合评价,确定每个因素的Ri,也就是上面的图

针对工作绩效,他的因素集有4个,评价集也是

然后使用模糊综合评价计算出R1(确定隶属函数/模糊评价法,计算对应的R)

3,计算Bi

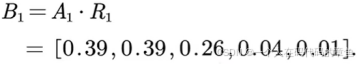
4,其他的并且存入原来的矩阵

5,计算最高级的B

这里面最大的是0.354,表示这个员工的最终评价结果是 良好

如果是更多级别的也是一样的,只是更多的套了一层娃

代码:

eval_mat=[

0.8,0.15,0.05,0,0;

0.2,0.6,0.1,0.1,0;

0.5,0.4,0.1,0.1,0;

0.1,0.3,0.5,0.05,0.05;

0.3,0.5,0.15,0.05,0;

0.2,0.2,0.4,0.1,0.1;

0.4,0.4,0.1,0.1,0;

0.1,0.3,0.3,0.2,0.1;

0.3,0.2,0.2,0.2,0.1;

0.1,0.3,0.5,0.1,0;

0.2,0.3,0.3,0.1,0.1;

0.2,0.3,0.35,0.15,0;

0.1,0.3,0.4,0.1,0.1;

0.1,0.4,0.3,0.1,0.1;

0.3,0.4,0.2,0.1,0.0;

0.1,0.4,0.3,0.1,0.1;

0.2,0.3,0.4,0.1,0.0;

0.4,0.3,0.2,0.1,0;

];%读入矩阵,针对不同的题,需要修改

disp('eval matrix:');

disp(eval_mat);

[m,n]=size(eval_mat);

w_mat={

[0.2,0.3,0.3,0.2],

[0.3,0.2,0.1,0.2,0.2],

[0.1,0.2,0.3,0.2,0.2],

[0.3,0.2,0.2,0.3]

};%这里面要写入权重,第一行写入因素1的子因素的各个的权重,依次向下写

w_eval=[0.4,0.3,0.2,0.1];%这里写入最高级的权重,对应的就是工作绩效,工作态度..的权重

eval_mat_second=[];

p=1;         %指针

for i =1:length(w_mat)

eval_mat_second =[eval_mat_second ;w_mat{i}*eval_mat(p:p+length(w_mat{i})-1,:)];

%这里的w_mat{i}*eval_mat(p:p+length(w_mat{i})-1,:) 是Bi,这个操作是把计算的Bi按列拼接到另外一个矩阵后面

p=p+length(w_mat{i}); %指针后移

end

disp('The first-level evalution:');

disp(eval_mat_second);

eval_vec=w_eval*eval_mat_second;

disp('the end');

disp(eval_vec);