带你从入门到精通——知识图谱（三. BiLSTM-CRF模型）

梦想是成为算法高手

已于 2025-04-02 15:30:29 修改

阅读量1.6k

点赞数 26

分类专栏：知识图谱文章标签：知识图谱人工智能 BiLSTM-CRF 深度学习神经网络动态规划实体抽取

于 2025-03-31 23:29:23 首次发布

本文链接：https://blog.csdn.net/2401_86480334/article/details/146884940

版权

知识图谱专栏收录该内容

6 篇文章

订阅专栏

建议先阅读我知识图谱专栏中的前置博客，掌握一定的知识图谱前置知识后再阅读本文，链接如下：

知识图谱_梦想是成为算法高手的博客-CSDN博客

三. BiLSTM-CRF模型

3.1 模型架构

BiLSTM-CRF模型的整体架构图如下：

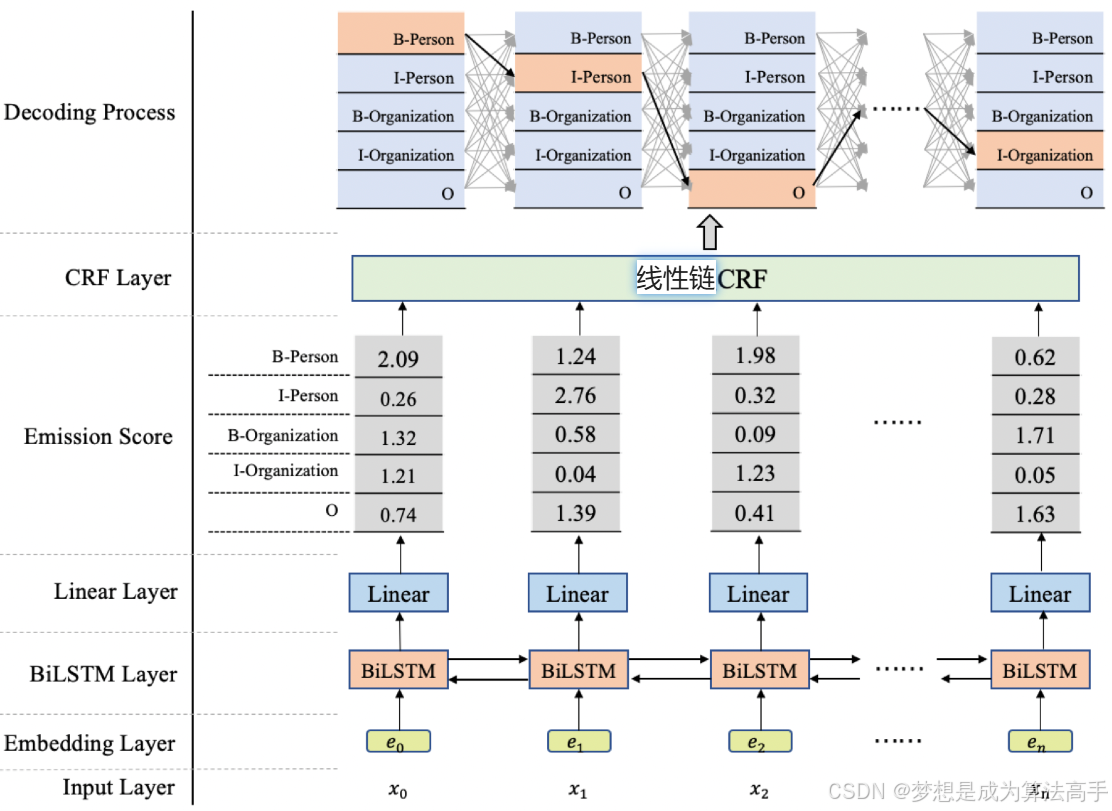
BiLSTM-CRF模型主要由五个部分构成：输入层、embedding层、BiLSTM层、Linear层、CRF层以及解码输出层，这里的CRF指的是线性链CRF。

其中，输入层用于接收形状为[batch_size，seq_len]的输入序列。

embedding层用于将输入序列映射为词向量，输出一个形状为[batch_size，seq_len，embedding_size]的张量。

BiLSTM层用于提取embedding后的输入序列的特征，输出一个形状为[batch_size，seq_len，hidden_size]的张量。

Linear层用于将hidden_size映射到标签数量label_size，输出一个形状为[batch_size，seq_len，label_size]的张量，该张量即为CRF层的发射张量，其中的元素值也被称为发射分数。

CRF层用于建模标签之间的关联，CRF层中有三个参数，start_transitions、end_transitions以及transitions，其中transitions即为转移矩阵，其形状为[label_size，label_size]，其中的元素值也被称为转移分数，start_transitions和end_transitions是起始转移向量和结束转移向量，其形状为[label_size]。

解码输出层则用于输出最优的标签序列。

3.2 前向传播和损失计算

BiLSTM-CRF模型的前向传播过程可以分为两个阶段，第一阶段是使用神经网络进行特征提取的过程，即将输入序列x转换为发射张量的过程，这里与正常的深度学习模型的前向传播一致，不再赘述；第二阶段是使用CRF层进行解码的过程，最终输出最优的标注序列。

CRF层进行解码的过程是选取有着最大路径分数的最优序列的过程，这里的路径分数的计算公式为：初始转移分数（即起始转移向量中起始序列位置的标签的对应值） + 各个序列位置的发射分数 + 各个序列位置对的之间转移分数 + 结束转移分数（即结束转移向量中结束序列位置的标签的对应值）。

如果计算出每个序列的路径分数后，再取路径分数最大的序列，这样的时间复杂度是指数级的 $O(T^{K})$ ，其中T为seq_len，K为label_size，可以使用动态规划的思想将这一过程的时间复杂度降低为 $O(TK^{2})$ ，假设T = K = 3，则CRF层的解码过程可以视为求下图的最短路径的问题：

具体实现步骤如下：

1. 初始化一个形状为T * K的二维dp数组，用于记录以某一节点为结尾的最优序列（有着最大路径分数的序列）的路径分数以及该最优序列的前驱节点。

2. 遍历T和K，更新二维dp数组中的内容，设当前遍历到的节点为N，即选取N所有前驱节点中有着最大路径分数的前驱节点，并在该前驱节点记录的路径分数的基础上加上N对应的发射分数和转移分数作为新的路径分数，在N中记录新的路径分数以及该前驱节点。

3. 向前回溯得到最优序列。

该算法也被成为Viterbi算法，通常用于计算在给定输入序列x的条件下，出现概率最大的标签序列y。

BiLSTM-CRF模型的损失函数定义如下：

即真实标签序列出现的负对数似然概率，其中 $S_{real}$ 为真实标签序列的路径分数， $S_{j}$ 为任意一个标签序列的路径分数，上式中的分母也被成为归一化因子。

化简后得到最终的损失函数：

在计算归一化因子的对数时，如果计算出每个序列的路径分数后，再求这些路径分数的指数和的对数，这样的时间复杂度同样是指数级的 $O(T^{K})$ ，同样可以使用动态规划的思想将这一过程的时间复杂度降低为 $O(TK^{2})$ ，该算法与Viterbi算法即为相似，具体实现步骤如下：

1. 初始化一个形状为T * K的二维dp数组，用于记录以某一节点为结尾的所有路径的路径分数的指数和的对数，形如： $log_{e}(e^{s_{1}} + e^{s_{2}}+ e^{s_{3}})$ ，后续直接简称为对数分数。

2. 遍历T和K，更新二维dp数组中的内容，设当前遍历到的节点为N，这里的更新步骤可以分为两步，第一步是在N的所有前驱节点所记录的对数分数中加上N的发射分数和转移分数，设N的发射分数和转移分数的和为x，这里需要将x转换为 $log_{e}(e^{x})$ 才能够添加到前驱节点所记录的对数分数中，添加x后的对数分数形如： $log_{e}(e^{s_{1} + x} + e^{s_{2} + x}+ e^{s_{3} + x})$ ；第二步是合并所有加上x后的前驱节点所记录的对数分数，这里的合并也不是直接相加，而是使用公式 $log_{e}(e^{y_{1}} + e^{y_{2}} + ... + e^{y_{n}})$ 进行合并，这里的y即为加上x后的前驱节点所记录的对数分数，最后在N中记录合并后的结果。

该算法也被成为前向算法，通常用于计算在给定输入序列x的条件下，所有可能的标签序列的对数分数和。

注意：计算形如 $log_{e}(e^{s_{1}} + e^{s_{2}}+ e^{s_{3}})$ 的具体值时，如果指数Si过大，可能会出现数值溢出的情况，通常使用log-sum-exp技巧计算，以防止数值溢出，log-sum-exp技巧即为提出最大的指数，将原式变形为： $s_{max} + log_{e}(e^{s_{1} - s_{max}} + e^{s_{2} - s_{max}}+ e^{s_{3} - s_{max}})$ 。

3.3 模型示例

BiLSTM-CRF模型的实现示例如下：

import torch.nn as nn
from torchcrf import CRF
from entity_extract.utils.dataloader import word2id

class NERLSTMCRF(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.name = config.model
        self.embedding_size = config.embedding_size
        self.hidden_size = config.hidden_size
        self.vocab_size = len(word2id)
        self.tag_size = len(config.tag2id)
        self.embedding = nn.Embedding(self.vocab_size, self.embedding_size)
        self.lstm = nn.LSTM(self.embedding_size, self.hidden_size // 2, batch_first=True, bidirectional=True)
        self.dropout = nn.Dropout(config.droupout)
        self.fc = nn.Linear(self.hidden_size, self.tag_size)
        self.crf = CRF(self.tag_size, batch_first=True)

    def getEmissionScore(self, x, mask):
        x = self.embedding(x)
        x, (h, c) = self.lstm(x)
        # mask张量的原始shape为[batch_size, seq_len], 需要升维后与x张量相乘进行mask
        x = x * mask.unsqueeze(-1)
        x = self.dropout(x)
        x = self.fc(x)
        return x

    def forward(self, x, mask):
        x = self.getEmissionScore(x, mask)
        # decode()方法返回的是一个二维列表，列表中每个元素是一个序列的标注结果
        x = self.crf.decode(x, mask=mask.bool())
        return x

    def getLoss(self, x, tags, mask):
        x = self.getEmissionScore(x, mask)
        # 输出的是对数似然概率，需要取负号得到负对数似然概率，
        # reduction='sum'为默认值，即求batch内的损失和， reduction='mean'为求batch内的平均损失
        return -self.crf(x, tags, mask=mask.bool(), reduction='mean')