1.3 函数 【上】

映射的概念

简单概念

如果集合 $X$ 的每一个元素 $x$ 都按照某规律 $f$ 与集合 $Y$ 的某一个元素 $y$ 对应，我们就说有一个映射，它定义于 $X$ 并取值于 $Y$ .

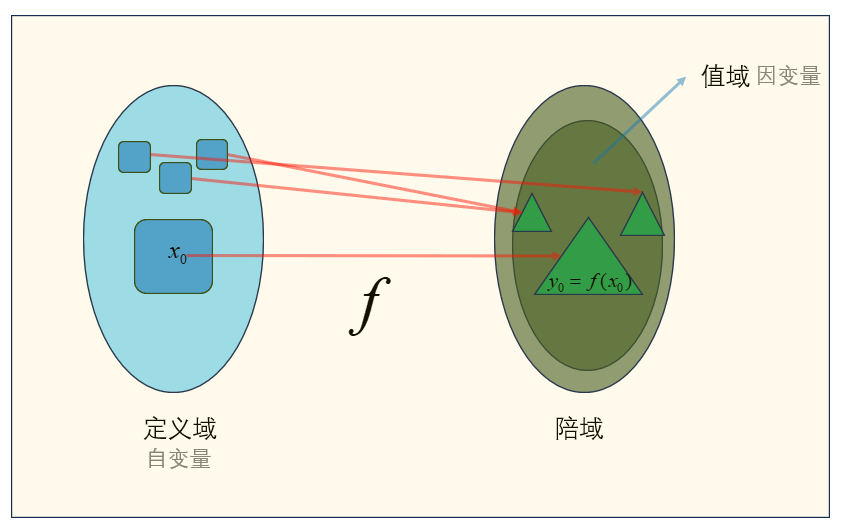
映射的值域定义为

f ( X ) : = { y ∈ Y ∣ ∃ x ( ( x ∈ X ) ∧ ( y = f ( x ) ) ) } f(X):=\{y\in Y|\exists x((x\in X)\wedge (y=f(x)))\} f(X):={y∈Y∣∃x((x∈X)∧(y=f(x)))}

在不同的领域，由于定义域 $X$ 和陪域 $Y$ 的组成元素不同，映射有着许许多多的实例名，如变换、射、算子、泛函、函数等。

映射的常用表达为 $f:X\to Y$

映射相等

如果映射 $f_1$ 和 $f_2$ 有相同的定义域 $X$，而且对于任何的 $x\in X$ , 都有 $f_1(x)=f_2(x)$ , 则称这两个映射相同或相等

对于映射 $f:X\to Y$ , 可以将映射关系限制在 $X$ 的子集 $A$ 上，构成 $f{|}_A:A\to Y$ , 在 $A$ 上 , $f(x)=f_A(x)$ .

也可以将映射关系延拓到 $X$ 的超集 $B$上 , 构成 $f{|}^B:B\to Y$ , 在 $X$ 上，$f(x)=f^B(x)$. 而在 $C_{B}X$ 上 , $f{|}^B$ 可以有其它定义.

映射是有方向的，从定义域集合到陪域集合。

映射的一些实例

【圆的周长公式和球的体积公式】 表达式 $l=2\pi r$ 建立了映射 $f:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ ，每个半径 $r$ , 都映射到了一个周长 $l=f(r)$ . 表达式 $V=\frac{4}{3}\pi r^3$ 建立了映射 $f:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ ，每个半径 $r$ , 都映射到了一个体积 $V=f(r)$ .

---

【光速的常数映射】 设 $X$ 是惯性坐标系的集合，映射 $c:X\to \mathbb{R}$ 给出了惯性坐标系 $x\in X$ 与相对于它测量的真空光速 $c(x)$ 的对应关系. 事实上，根据实验事实，对于任意的 $x\in X$ 都有 $c(X)=c_0$ . 其中 $c_0$ 为固定的真空光速值.

---

【伽利略变换与一维洛伦兹变换】

$\{\begin{array}{l}{x}^{\prime }=x-vt\\ t^{\prime }=t\end{array}$ 给出的映射 $G:{\mathbb{R}}^2\to {\mathbb{R}}^2$ 是经典的伽利略变换，它从一个惯性坐标系 $(x,t)$ 变换到另一个惯性坐标系 $(x^{\prime },t^{\prime })$ , 后者相对于前者以速度 $v$ 运动.

$\{\begin{array}{l}{x}^{\prime }=\frac{x-vt}{\sqrt{1-(\frac{v}{c}}{)}^2}\\ t^{\prime }=\frac{t-(\frac{v}{c^2})x}{\sqrt{1-(\frac{v}{c}}{)}^2}\end{array}$ 给出的洛伦兹变换 $L:{\mathbb{R}}^2\to {\mathbb{R}}^2$ 起到了相同的作用，在狭义相对论中起基本作用.其中 $c$ 是光速大小.

---

【投影映射】 第一投影 ${\text{pr}}_1:X_1\times X_2\to X_1$ 由对应关系 $x_1={\text{pr}}_1(x_1,x_2)$ 给出。 第二投影 ${\text{pr}}_2:X_1\times X_2\to X_2$ 由对应关系 $x_2={\text{pr}}_1(x_1,x_2)$ 给出。

---

【补集】 设 $\mathcal{P}(M)$ 是集合 $M$ 的全部子集的集合. 让每一个 $A\in \mathcal{P}(M)$ 与集合 $C_M(A)\in \mathcal{P}(M)$ 相对应.$C_M(A)$ 就是我们前面提到的 $A$ 的补集. 可见，补集运算 $C_M$ 是一个从 $\mathcal{P}(M)$ 到 $\mathcal{P}(M)$ 本身的映射.

---

【特征函数】 设 $E\subset M$. 由表达式 ${\chi }_E(x)=\{\begin{array}{ll}1& x\in E\\ 0& x\notin E\end{array}$ 确定的映射 ${\chi }_E:M\to \mathbb{R}$ 被称为集合 $E$ 的特征函数.

---

【泛函】 设 $M(X;Y)$ 是从集合 $X$ 到集合 $Y$ 的映射的集合，而 $x_0$ 是 $X$ 的一个固定元素. 让每一个映射 $f\in M(X;Y)$ 都与该映射在 $x_0$ 上的取值 $f(x_0)\in Y$ 相对应，从而定义了映射上的映射 $F:M(X;Y)\to Y$. 特别地，如果 $Y=\mathbb{R}$ , 则每个函数 $f$ 都与一个实数 $F(f)=f(x_0)$ 相对应，$F$ 是定义在函数上的函数，这样的函数被称为泛函.

---

【测地线】 设 $\Gamma$ 是曲面上连接两个固定点的曲线的集合. 可以让每一条曲线 $\gamma \in \Gamma$ 与其长度相对应，从而得到映射 $F:\Gamma \to \mathbb{R}$ . 人们在研究给定两点之间求最短曲线的问题时，常常要考虑这样的函数.

---

【平移算子】 设 $M(\mathbb{R},\mathbb{R})$ 是从 $\mathbb{R}$ 到 $\mathbb{R}$ 的所有实值函数的集合. 给定一个固定的偏移量 $a$ , 让每个 $f\in M(\mathbb{R},\mathbb{R})$ 对应于一个新的函数 $f_a\in M(\mathbb{R},\mathbb{R})$ , 对应法则为 $f_a(x)=f(x+a)$ . 这样生成的映射 $A:M(\mathbb{R},\mathbb{R})\to M(\mathbb{R},\mathbb{R})$ 称为 $a$ 平移算子.平移算子生成 $f$ 的平移 $f_a=A(f)$，它也是定义在函数上的映射.

事实上，像收音机这样的接收装置也自带了算子 ，它们把电磁信号 $f$ 转变为 声信号 $\hat{f}=F(f)$

---

【质点系统】 一个质点在空间中的位置由坐标 $(x,y,z)$ 确定 . 所有坐标组成的集合可以看做 ${\mathbb{R}}^3=\mathbb{R}\times \mathbb{R}\times \mathbb{R}$ .

在某一时刻 $t$ , 质点的位置由 $(x(t),y(t),z(t))$ 表示. 由此，质点的运动过程可以看成是一个映射 $\gamma :{\mathbb{R}}_t\to {\mathbb{R}}^3$ , 由时间轴映射到三维空间.

如果一个系统由 $n$ 个质点组成，那么它的构形可以由各质点的位置共同表出，即由有序的 $3n$ 个数 $(x_1,y_1,z_1;x_2,y_2,z_2;\cdots ;x_n,y_n,z_n)$ 表出. 所有这样的有序的数的集合称为 $n$ 质点系的构型空间. 它可以表示为 ${\mathbb{R}}^{3n}={\mathbb{R}}^3\times \cdots \times {\mathbb{R}}^3$ .

时间轴到质点系构形空间的映射 $\gamma :\mathbb{R}\to {\mathbb{R}}^{3n}$ 对应着 $n$ 质点系的运动.

---

【势能】 力学系统中的势能 $U$ 与其质点的相互位置有关，即和系统的构形有关. 设 $Q$ 是系统实际可能具有的构形的集合，每个构形 $q\in Q$ 都对应着系统势能的某个值 $U(q)$ . 因此，势能可以表示为映射 $U:Q\to \mathbb{R}$ .

---

【机械能】 $n$ 质点系的动能 $K$ 与各质点的速度有关. 而质点系的总机械能 $E=K+U$ , 既与质点系的构形 $q$ 有关，又与各质点的速度数组 $v$ 有关. $v$ 也由 $n$ 个三维向量构成，也取值于 ${\mathbb{R}}^{3n}$. 与质点系状态相对应的序偶 $(q,v)$ 组成了 ${\mathbb{R}}^6$ 的一个子集 $\Phi$ ，称为 $n$ 质点系的相空间.

由此，系统的总机械能可以表示为映射 $E:\Phi \to \mathbb{R}$.特别地，如果系统的机械能守恒，则 $E$ 在系统相空间的所有状态下都取相同的值 $E_0\in \mathbb{R}$

---

映射的简单分类

满射

当 $f(X)=Y$ 时，映射 $f:X\to Y$ 称为满射，又称到上映射.

映满

单射

对于任意的 $x_1,x_2\in X$ , $(f(x_1)=f(x_2))\Rightarrow (x_1=x_2)$ 成立

不同元素具有不同的像

双射与互逆映射

既是单射又是满射的映射称为双射.

对于单射 $f:X\to Y$ ，新映射 $g:X\to f(X)$ 即为双射.

对于双射 $f:X\to Y$ ，每一个 $x\in X$ 都与唯一的的 $y\in Y$ 对应，每一个 $y\in Y$ 都与唯一的的 $x\in X$ 对应.

也就是说 , $x$ 与 $y$ 一一对应.

对于双射，对应关系为 $x=f^{-1}(y)$的映射 $f^{-1}:Y\to X$ 也是符合定义的，通常称为 $f$ 的逆映射.

逆映射也是双射，而且逆映射的逆映射 $(f^{-1}{)}^{-1}:X\to Y$ 就是本身 $f:X\to Y$.

映射的复合与互逆映射

概念

映射的复合运算，一方面可以用于生成丰富的新函数，另一方面可以用于分解复杂函数.

设有映射 $f:X\to Y$ 和 $g:Y\to Z$ , 这时可以构造一个新的映射 $g\circ f:X\to Z$ , 对应关系由 $(g\circ f)(x):=g(f(x))$ 确定. 有着这样多层映射关系的映射称为复合映射.

映射可以多层复合.

复合的结合律

$h\circ (g\circ f)=(h\circ g)\circ f$

如果复合映射 $f_n\circ f_{n-1}\cdots f_2\circ f_1$ 中所有的单个映射都相同且为 $f$ ，就可以把它简写为 $f^n$

常见的迭代过程 $x_n=f(x_{n-1})$ 就可以看作一个 $f_n$

复合映射 $g\circ f$ 存在 ，$f\circ g$ 可能不存在，二者也就没有必然的相等关系，故交换律不存在

恒等映射

满足对应关系 $f(x)=x$ 的映射 $f:X\to X$ 称为恒等映射，记 $e_X$ 为集合 $X$ 上的恒等映射. 恒等映射是双射.

$(g\circ f=e_X)\Rightarrow (g是满射)\wedge (f是单射)$

**证明：**设 $g\circ f=e_X$ ，$f:X\to Y$ ， $g:Y\to X$ .

$X=e_X(X)=(g\circ f)(X)=g(f(X))\subset g(Y)$ . 故 $X=g(Y)$ ，即 $g$ 是满射

设 $x_1\ne x_2\in X$ , 则

$(x_1\ne x_2)\Rightarrow (g\circ f)(x_1)\ne (g\circ f)(x_2)\Rightarrow g(f(x_1))\ne g(f(x_2))\Rightarrow f(x_1)\ne f(x_2)$ .

故 $f$ 是单射

映射 $f:X\to Y$ ，$g:Y\to X$ 是互逆的双射 $\iff$ $g\circ f=e_X,f\circ g=e_Y$

假设映射 $f:X\to Y$ ，$g:Y\to X$ 是互逆的双射.

$(g\circ f)(x)=g(f(x))=g(y)=x,(f\circ g)(y)=f(g(y))=f(x)=y$

假设 $g\circ f=e_X,f\circ g=e_Y$ ,

则 $(g是满射)\wedge (f是单射)\wedge (f是满射)\wedge (g是单射)$ , 即 $f,g$ 都是双射

且 $(g\circ f)(x)=g(f(x))=x=g(y),(f\circ g)(y)=f(g(y))=y=f(x)$ , 即 $f$ 与 $g$ 互逆

关系与函数图像

前面映射概念的描述其实是一种反应其本质的相对动态的描述，从现代标准看，其实并不能称之为定义，因为它使用到了一个与映射等价的概念——对应.

关系

序偶 $(x,y)$ 的任何集合称为关系 $\mathcal{R}$ .

组成 $\mathcal{R}$ 的一切序偶的第一坐标组成的集合 $X$ 称为 $\mathcal{R}$ 的定义域，第二坐标组成的集合 $Y$ 称为 $\mathcal{R}$ 的值域

因此，可以把关系 $\mathcal{R}$ 理解为 $X\times Y$ 的子集.

常常把 $(x,y)\in \mathcal{R}$ 写作 $x\mathcal{R}y$ , 并称 $x$ 与 $y$ 具有关系 $\mathcal{R}$.

如果 $\mathcal{R}\in X^2$, 就说在 $X$ 上给定了关系 $\mathcal{R}$ .

关系的一些实例

【相等关系】 笛卡尔积 $X^2$ 的对角线 $\Delta =\{(a,b)\in X^2|a=b\}$ 给出 $X$ 上的相等关系. 其实 $a\Delta b$ 就表示 $(a,b)\in \Delta \Rightarrow a=b$ .

---

【等价关系】 设 $X$ 是平面上的直线的集合. 如果直线 $b\in X$ 平行于直线 $a\in X$，我们就认为这两条直线之间具有关系 $\mathcal{R}$，即构造一个集合，使得所有平行的直线 $a,b$ 组成的序偶 $(a,b)\in \mathcal{R}$ .显然，这样就从 $X^2$ 中划分出了一个平行关系 $\mathcal{R}$ .

根据几何知识，直线的平行关系 $\mathcal{R}$ 满足下面的三个性质：

• 自反性：$a\mathcal{R}a$
• 对称性：$a\mathcal{R}b\Rightarrow b\mathcal{R}a$
• 传递性：$(a\mathcal{R}b)\wedge (b\mathcal{R}c)\Rightarrow a\mathcal{R}c$

任何具有自反性、对称性、传递性的关系 $\mathcal{R}$ 通常称为等价关系，

对于等价关系，我们把 $a\mathcal{R}b$ 写作 $a\sim b$ ，并说 $a$ 与 $b$ 等价

---

【偏序关系】 设 $M$ 是某集合，$X=\mathcal{P}(M)$ 的任意两个元素 $a$ 与 $b$ 之间，只有以下三种可能：$a\subset b$ 或 $b\subset a$ 或 $\neg ((a\subset b)\wedge (b\subset a))$

可以定义包含关系 $a\mathcal{R}b:=(a\subset b)$ ，这个关系显然具有以下性质：

• 自反性：$a\mathcal{R}a$
• 反对称性：$(a\mathcal{R}b)\wedge (b\mathcal{R}a)\Rightarrow a=b$
• 传递性：$(a\mathcal{R}b)\wedge (b\mathcal{R}c)\Rightarrow a\mathcal{R}c$

任何具有自反性、反对称性、传递性的关系 $\mathcal{R}$ 通常称为偏序关系，

对于偏序关系，我们把 $a\mathcal{R}b$ 写作 $a⪯b$ ，并说 $b$ 在 $a$ 之后 .

---

【序关系】 如果对于集合 $X$ 和$X$ 上的关系 $\mathcal{R}$ 有

• 任意两元素可比，即 $\forall a\forall b((a\mathcal{R}b)\vee (b\mathcal{R}a))$
• $\mathcal{R}$是偏序

那么称 $\mathcal{R}$ 为序关系. 定义了序关系的集合 $X$ 称为线性序集.

---

函数关系

满足 $(x\mathcal{R}{y}_1)\wedge (x\mathcal{R}{y}_2)\Rightarrow (y_1=y_2)$ 的关系 $\mathcal{R}$ 称为函数关系. 也就是说每一个 $x$ 有唯一的 $y$ 与其具有关系 $\mathcal{R}$ .

函数关系一般可以用 $f$ 表示，$xfy$ 通常记作 $y=f(x)$

$\{(x,y)|y=f(x)\}$ 是 ${\mathbb{R}}^2$ 的子集，可以将其描点画于平面坐标系中，称之为函数图像.