习题
【1】关系的复合
关系 R 1 , R 2 \mathcal{R_1},\mathcal{R_2} R1,R2 的复合 R 2 ∘ R 1 R_2\circ R_1 R2∘R1 定义为 R 2 ∘ R 1 : = { ( x , z ) ∣ ∃ y ( ( x R 1 y ) ∧ ( y R 2 z ) ) } R_2\circ R_1:=\{(x,z)|\exists y((x\mathcal{R_1}y)\wedge (y\mathcal{R}_2z))\} R2∘R1:={(x,z)∣∃y((xR1y)∧(yR2z))} .
a) 设 Δ X , Δ Y \Delta_X,\Delta_Y ΔX,ΔY 分别是 X 2 , Y 2 X^2,Y^2 X2,Y2 的对角线. 请证明:如果关系 R 1 ⊂ X × Y \mathcal{R}_1\subset X\times Y R1⊂X×Y 与 R 2 ⊂ Y × X \mathcal{R}_2\subset Y\times X R2⊂Y×X 满足 ( R 2 ∘ R 1 = Δ X ) ∧ ( R 1 ∘ R 2 = Δ Y ) (R_2\circ R_1=\Delta_X)\wedge(R_1\circ R_2=\Delta_Y) (R2∘R1=ΔX)∧(R1∘R2=ΔY),则它们都是函数关系并且给出 X , Y X,Y X,Y 之间的互逆映射.
证明:
假设 ( x R 1 y 1 ) ∧ ( x R 1 y 2 ) (x\mathcal{R}_1y_1)\wedge(x\mathcal{R}_1y_2) (xR1y1)∧(xR1y2) 成立.
由 R 2 ∘ R 1 = Δ X R_2\circ R_1=\Delta_X R2∘R1=ΔX 得 ( y 1 R 2 x ) ∧ ( y 2 R 2 x ) (y_1\mathcal{R}_2x)\wedge(y_2\mathcal{R}_2x) (y1R2x)∧(y2R2x) .
由 ( y 1 R 2 x ) ∧ ( x R 1 y 2 ) (y_1R_2x)\wedge(xR_1y_2) (y1R2x)∧(xR1y2) 知 y 1 ( R 1 ∘ R 2 ) y 2 y_1(\mathcal{R}_1\circ\mathcal{R}_2)y_2 y1(R1∘R2)y2
由 R 1 ∘ R 2 = Δ Y R_1\circ R_2=\Delta_Y R1∘R2=ΔY 得 y 1 = y 2 y_1=y_2 y1=y2 .
故 ( x R 1 y 1 ) ∧ ( x R 1 y 2 ) ⇒ ( x R 1 y 1 ) ∧ ( x R 1 y 2 ) (x\mathcal{R}_1y_1)\wedge(x\mathcal{R}_1y_2)\Rightarrow (x\mathcal{R}_1y_1)\wedge(x\mathcal{R}_1y_2) (xR1y1)∧(xR1y2)⇒(xR1y1)∧(xR1y2) , 即 R 1 R_1 R1 是函数关系
同理可证 R 2 \mathcal{R}_2 R2 是函数关系.
既然 R 1 \mathcal{R}_1 R1 和 R 2 \mathcal{R}_2 R2 都是函数关系,容易看出,他们确定的函数
y = f 1 ( x ) y=f_1(x) y=f1(x) 和 x = f 2 ( y ) x=f_2(y) x=f2(y) 为互逆映射
b) 设 R 2 ⊂ X 2 \mathcal{R}^2\subset X^2 R2⊂X2. 证明:关系 R \mathcal{R} R 的传递性等价于 R ∘ R ⊂ R \mathcal{R}\circ \mathcal{R}\subset \mathcal{R} R∘R⊂R.
证明:
假设关系 R \mathcal{R} R 具有传递性,即对于任意的 a , b , c ∈ X a,b,c\in X a,b,c∈X 有 ( a R b ) ∧ ( b R c ) ⇒ a R c (a\mathcal{R}b)\wedge(b\mathcal{R}c)\Rightarrow a\mathcal{R}c (aRb)∧(bRc)⇒aRc
a ( R ∘ R ) c ⇒ ∃ b ( ( a R b ) ∧ ( b R c ) ) ⇒ a R c a(\mathcal{R}\circ \mathcal{R})c\Rightarrow \exists b((a\mathcal{R}b)\wedge(b\mathcal{R}c)) \Rightarrow a\mathcal{R}c a(R∘R)c⇒∃b((aRb)∧(bRc))⇒aRc
这说明 R ∘ R ⊂ R \mathcal{R}\circ \mathcal{R}\subset \mathcal{R} R∘R⊂R
假设 R ∘ R ⊂ R \mathcal{R}\circ \mathcal{R}\subset \mathcal{R} R∘R⊂R , 则对于任意的 a , b , c ∈ X a,b,c\in X a,b,c∈X
( a R b ) ∧ ( b R c ) ⇒ a ( R ∘ R ) c ⇒ a R c (a\mathcal{R}b)\wedge(b\mathcal{R}c)\Rightarrow a(\mathcal{R}\circ \mathcal{R})c \Rightarrow a\mathcal{R}c (aRb)∧(bRc)⇒a(R∘R)c⇒aRc
这说明关系 R \mathcal{R} R 具有传递性
c) 如果关系 R ′ ⊂ Y × X \mathcal{R'}\subset Y\times X R′⊂Y×X 和 R ⊂ X × Y \mathcal{R}\subset X\times Y R⊂X×Y 满足 ( y R ′ x ) ⇔ x R y (y\mathcal{R}'x)\Leftrightarrow x\mathcal{R}y (yR′x)⇔xRy,则称 R ′ \mathcal{R}' R′ 为 R \mathcal{R} R 的转置关系. 证明:关系 R ⊂ X 2 \mathcal{R}\subset X^2 R⊂X2 的反对称性等价于条件 R ∩ R ′ ⊂ Δ X \mathcal{R}\cap \mathcal{R}'\subset \Delta_X R∩R′⊂ΔX .
证明:
假设关系 R \mathcal{R} R 具有反对称性,即对于任意的 a , b ∈ X a,b\in X a,b∈X 有 ( a R b ) ∧ ( b R a ) ⇒ a = b (a\mathcal{R}b)\wedge (b\mathcal{R}a)\Rightarrow a=b (aRb)∧(bRa)⇒a=b
a ( R ∩ R ′ ) b ⇒ ( a R b ) ∧ ( a R ′ b ) ⇒ ( a R b ) ∧ ( b R a ) a(\mathcal{R}\cap \mathcal{R}')b\Rightarrow (a\mathcal{R}b)\wedge (a\mathcal{R}'b) \Rightarrow (a\mathcal{R}b)\wedge (b\mathcal{R}a) a(R∩R′)b⇒(aRb)∧(aR′b)⇒(aRb)∧(bRa)
⇒ a = b ⇒ a Δ X b \Rightarrow a=b \Rightarrow a\Delta_X b ⇒a=b⇒aΔXb . 这说明 R ∩ R ′ ⊂ Δ X \mathcal{R}\cap \mathcal{R}'\subset \Delta_X R∩R′⊂ΔX .
假设 R ∩ R ′ ⊂ Δ X \mathcal{R}\cap \mathcal{R}'\subset \Delta_X R∩R′⊂ΔX . 则对于任意的 a , b ∈ X a,b\in X a,b∈X 有 ( a R b ) ∧ ( b R a ) (a\mathcal{R}b)\wedge (b\mathcal{R}a) (aRb)∧(bRa)
⇒ ( a R b ) ∧ ( a R ′ b ) ⇒ a ( R ∩ R ′ ) b ⇒ a Δ X b ⇒ a = b \Rightarrow (a\mathcal{R}b)\wedge (a\mathcal{R}'b)\Rightarrow a(\mathcal{R}\cap \mathcal{R}')b \Rightarrow a\Delta_X b\Rightarrow a=b ⇒(aRb)∧(aR′b)⇒a(R∩R′)b⇒aΔXb⇒a=b
这说明关系 R \mathcal{R} R 具有反对称性 .
d) 证明:当且仅当 R ∪ R ′ = X 2 \mathcal{R}\cup \mathcal{R}'=X^2 R∪R′=X2 时,集合 X X X 的任意两个元素之间由 R ⊂ X 2 R\subset X^2 R⊂X2 相联系.
证明:
R ∪ R ′ = X 2 ⇔ 对于任意的 a , b ∈ X , 必定有 a ( R ∪ R ′ ) b \mathcal{R}\cup \mathcal{R}'=X^2 \Leftrightarrow 对于任意的 a,b\in X , 必定有 a(\mathcal{R}\cup \mathcal{R}')b R∪R′=X2⇔对于任意的a,b∈X,必定有a(R∪R′)b
⇔ ( a R b ) ∨ ( a R ′ b ) ⇔ ( a R b ) ∨ ( b R a ) \Leftrightarrow (a\mathcal{R}b)\vee(a\mathcal{R'}b)\Leftrightarrow (a\mathcal{R}b)\vee(b\mathcal{R}a) ⇔(aRb)∨(aR′b)⇔(aRb)∨(bRa)
【2】层
设 f : X → Y f:X\to Y f:X→Y 是映射. 元素 y ∈ Y y\in Y y∈Y 的原像 f − 1 ( y ) ⊂ X f^{-1}(y)\subset X f−1(y)⊂X 称为 y y y 上的层.
a) 请指出映射 pr 1 : X 1 × X 2 → X 1 , pr 2 : X 1 × X 2 → X 2 \text{pr}_1:X_1\times X_2\to X_1,\text{pr}_2:X_1\times X_2\to X_2 pr1:X1×X2→X1,pr2:X1×X2→X2 的层
解:
任给 x 1 ∈ X 1 x_1\in X_1 x1∈X1 , x 1 x_1 x1 的层 pr 1 − 1 ( x 1 ) = { ( x 1 , y ) ∣ y ∈ X 2 } \text{pr}_1^{-1}(x_1)=\{(x_1,y)|y\in X_2\} pr1−1(x1)={(x1,y)∣y∈X2}
任给 x 2 ∈ X 2 x_2\in X_2 x2∈X2 , x 2 x_2 x2 的层 pr 2 − 1 ( x 2 ) = { ( x , x 2 ) ∣ x ∈ X 1 } \text{pr}_2^{-1}(x_2)=\{(x,x_2)|x\in X_1\} pr2−1(x2)={(x,x2)∣x∈X1}
b) 设 x 1 , x 2 ∈ X x_1,x_2\in X x1,x2∈X ,如果 f ( x 1 ) = f ( x 2 ) f(x_1)=f(x_2) f(x1)=f(x2),即如果 x 1 x_1 x1 与 x 2 x_2 x2 位于同一层,就认为 x 1 x_1 x1 与 x 2 x_2 x2 由关系 R ⊂ X 2 \mathcal{R}\subset X^2 R⊂X2 相联系,并记为 x 1 R x 2 x_1\mathcal{R}x_2 x1Rx2 . 证明: R \mathcal{R} R 是等价关系
证明:
- 自反性: f ( x ) = f ( x ) ⇒ x R x f(x)=f(x)\Rightarrow x\mathcal{R} x f(x)=f(x)⇒xRx
- 对称性: x 1 R x 2 ⇒ f ( x 1 ) = f ( x 2 ) ⇒ f ( x 2 ) = f ( x 1 ) ⇒ x 2 R x 1 x_1\mathcal{R}x_2\Rightarrow f(x_1)=f(x_2)\Rightarrow f(x_2)=f(x_1) \Rightarrow x_2 \mathcal{R}x_1 x1Rx2⇒f(x1)=f(x2)⇒f(x2)=f(x1)⇒x2Rx1
- 传递性: ( x 1 R x 2 ) ∧ ( x 2 R x 3 ) ⇒ f ( x 1 ) = f ( x 2 ) = f ( x 3 ) ⇒ f ( x 1 ) = f ( x 3 ) ⇒ x 1 R x 3 (x_1\mathcal{R}x_2)\wedge(x_2\mathcal{R}x_3)\Rightarrow f(x_1)=f(x_2)=f(x_3)\Rightarrow f(x_1)=f(x_3)\Rightarrow x_1\mathcal{R}x_3 (x1Rx2)∧(x2Rx3)⇒f(x1)=f(x2)=f(x3)⇒f(x1)=f(x3)⇒x1Rx3
c) 证明:映射 f : X → Y f:X\to Y f:X→Y 的层互不相交,而所有层的并集就是整个集合 X X X .
证明:
假设存在 y 1 ≠ y 2 y_1\neq y_2 y1=y2,使得 f f f 的层 f − 1 ( y 1 ) f^{-1}(y_1) f−1(y1) 与 f − 1 ( y 2 ) f^{-1}(y_2) f−1(y2) 相交,
这说明存在 x x x , 使得 ( f ( x ) = y 1 ) ∧ ( f ( x ) = y 2 ) (f(x)=y_1)\wedge (f(x)=y_2) (f(x)=y1)∧(f(x)=y2) . 这与函数定义矛盾.
因此映射 f : X → Y f:X\to Y f:X→Y 的层互不相交.
所有层的并集包含于 X X X 是显然的. 对于任意的 x ∈ X x\in X x∈X , 存在 y = f ( x ) y=f(x) y=f(x) , 这说明 x ∈ f − 1 ( y ) x\in f^{-1}(y) x∈f−1(y) . 也就是说, X X X 包含于所有层的并集. 综合起来,所有层的并集就是整个集合 X X X .
d) 证明:利用集合的元素之间的任何等价关系,都可以把该集合表示为互不相交的等价元素类的并集的形式.
证明:
设 x ∼ = { y ∈ A ∣ y ∼ x } \overset{\sim}{x}=\{y\in A|y\sim x\} x∼={y∈A∣y∼x} ,称之为 x x x 的等价类.
假设 y ∼ x y\sim x y∼x .
z ∈ y ∼ ⇒ z ∼ y ⇒ z ∼ x ⇒ z ∈ x ∼ z\in \overset{\sim}{y} \Rightarrow z \sim y \Rightarrow z\sim x\Rightarrow z\in \overset{\sim}{x} z∈y∼⇒z∼y⇒z∼x⇒z∈x∼.
z ∈ x ∼ ⇒ z ∼ x ⇒ x ∼ z ⇒ y ∼ z ⇒ z ∼ y ⇒ z ∈ y ∼ z\in \overset{\sim}{x} \Rightarrow z \sim x \Rightarrow x \sim z\Rightarrow y\sim z\Rightarrow z\sim y \Rightarrow z\in \overset{\sim}{y} z∈x∼⇒z∼x⇒x∼z⇒y∼z⇒z∼y⇒z∈y∼
这说明 x ∼ = y ∼ \overset{\sim}{x}=\overset{\sim}{y} x∼=y∼ ,即具有等价关系的元素属于同一等价类
假设 y ≁ x y\nsim x y≁x .
z ∈ y ∼ ⇒ z ∼ y ⇒ z ≁ x ⇒ z ∉ x ∼ z\in \overset{\sim}{y} \Rightarrow z \sim y \Rightarrow z\nsim x\Rightarrow z\notin \overset{\sim}{x} z∈y∼⇒z∼y⇒z≁x⇒z∈/x∼
这说明 x ∼ ∩ y ∼ = ∅ \overset{\sim}{x}\cap\overset{\sim}{y}=\varnothing x∼∩y∼=∅ ,即不具有等价关系的元素属于的等价类互不相交
设所有的等价类组成的集合为 Q = { x ∼ ∣ x ∈ A } Q=\{\overset{\sim}{x} |x\in A\} Q={x∼∣x∈A} , 该集称为 A A A 的商集 Q Q Q
∪ x ∼ ∈ Q x ∼ ⊂ A \underset{\overset{\sim}{x}\in Q}\cup \overset{\sim}{x}\subset A x∼∈Q∪x∼⊂A 是显然的 . 对于每个 x ∈ A x\in A x∈A ,必然有 x ∈ x ∼ x\in \overset{\sim}{x} x∈x∼ , 故 A ⊂ ∪ x ∼ ∈ Q x ∼ A\subset \underset{\overset{\sim}{x}\in Q}\cup \overset{\sim}{x} A⊂x∼∈Q∪x∼ . 则 A = ∪ x ∼ ∈ Q x ∼ A=\underset{\overset{\sim}{x}\in Q}\cup \overset{\sim}{x} A=x∼∈Q∪x∼.
综上,该集合可以表示为互不相交的等价类 x ∼ \overset{\sim}x x∼ 的并集的形式.
【3】映射中的子集
有映射 f : X → Y f:X\to Y f:X→Y . 证明:如果 A A A 与 B B B 都是 X X X 的子集,则
a) ( A ⊂ B ) ⇒ ( f ( A ) ⊂ f ( B ) ) ⇏ ( A ⊂ B ) (A\subset B)\Rightarrow (f(A)\subset f(B)) \nRightarrow (A\subset B) (A⊂B)⇒(f(A)⊂f(B))⇏(A⊂B)
证明:
假设 A ⊂ B A\subset B A⊂B 成立 .
若 f ( A ) = ∅ f(A)=\varnothing f(A)=∅ , 则显然有 f ( A ) ⊂ f ( B ) f(A)\subset f(B) f(A)⊂f(B) .
若 f ( A ) f(A) f(A) 不为空集 , 则存在 y ∈ f ( A ) ⇒ y = f ( x ) , x ∈ A ⇒ y = f ( x ) , x ∈ B ⇒ y ∈ f ( B ) y\in f(A)\Rightarrow y=f(x),x\in A\Rightarrow y=f(x),x\in B\Rightarrow y\in f(B) y∈f(A)⇒y=f(x),x∈A⇒y=f(x),x∈B⇒y∈f(B)
即 f ( A ) ⊂ f ( B ) f(A)\subset f(B) f(A)⊂f(B) . 故 ( A ⊂ B ) ⇒ ( f ( A ) ⊂ f ( B ) ) (A\subset B)\Rightarrow (f(A)\subset f(B)) (A⊂B)⇒(f(A)⊂f(B)) .
可以构造 f : R → R f:\mathbb{R}\to \mathbb{R} f:R→R 为 f ( x ) = x 2 f(x)=x^2 f(x)=x2 .
取 A = [ − 1 , 1 ] , B = [ 0 , 1 ] A=[-1,1],B=[0,1] A=[−1,1],B=[0,1] , 则 f ( A ) = [ 0 , 1 ] = f ( B ) f(A)=[0,1]=f(B) f(A)=[0,1]=f(B) 但 B ⊂ A B\subset A B⊂A .
b) ( A ≠ ∅ ) ⇒ ( f ( A ) ≠ ∅ ) (A\neq \varnothing)\Rightarrow (f(A)\ne \varnothing) (A=∅)⇒(f(A)=∅)
证明:
A ≠ ∅ A\neq \varnothing A=∅ , 则可取 x ∈ A x\in A x∈A ,对应有 f ( x ) ∈ f ( A ) f(x)\in f(A) f(x)∈f(A) . 故 ( f ( A ) ≠ ∅ ) (f(A)\ne \varnothing) (f(A)=∅) .
c) f ( A ∩ B ) ⊂ f ( A ) ∩ f ( B ) f(A\cap B)\subset f(A)\cap f(B) f(A∩B)⊂f(A)∩f(B)
证明:
若 f ( A ∩ B ) = ∅ f(A\cap B)=\varnothing f(A∩B)=∅,则显然有 f ( A ∩ B ) ⊂ f ( A ) ∩ f ( B ) f(A\cap B)\subset f(A)\cap f(B) f(A∩B)⊂f(A)∩f(B) .
若 f ( A ∩ B ) ≠ ∅ f(A\cap B)\neq \varnothing f(A∩B)=∅,则存在 y ∈ f ( A ∩ B ) ⇒ y = f ( x ) , x ∈ A ∩ B ⇒ y = f ( x ) , ( x ∈ A ) ∧ ( x ∈ B ) y\in f(A\cap B)\Rightarrow y=f(x),x\in A\cap B \Rightarrow y=f(x),(x\in A)\wedge(x\in B) y∈f(A∩B)⇒y=f(x),x∈A∩B⇒y=f(x),(x∈A)∧(x∈B)
⇒ ( y ∈ f ( A ) ) ∧ ( y ∈ f ( B ) ) ⇒ y ∈ f ( A ) ∩ f ( B ) \Rightarrow (y\in f(A))\wedge(y\in f(B))\Rightarrow y\in f(A)\cap f(B) ⇒(y∈f(A))∧(y∈f(B))⇒y∈f(A)∩f(B)
d) f ( A ∪ B ) ⊂ f ( A ) ∪ f ( B ) f(A\cup B)\subset f(A)\cup f(B) f(A∪B)⊂f(A)∪f(B)
证明:
若 f ( A ∪ B ) = ∅ f(A\cup B)=\varnothing f(A∪B)=∅,则显然有 f ( A ∪ B ) ⊂ f ( A ) ∪ f ( B ) f(A\cup B)\subset f(A)\cup f(B) f(A∪B)⊂f(A)∪f(B) .
若 f ( A ∪ B ) ≠ ∅ f(A\cup B)\neq \varnothing f(A∪B)=∅,则存在 y ∈ f ( A ∪ B ) ⇒ y = f ( x ) , x ∈ A ∪ B ⇒ y = f ( x ) , ( x ∈ A ) ∨ ( x ∈ B ) y\in f(A\cup B)\Rightarrow y=f(x),x\in A\cup B \Rightarrow y=f(x),(x\in A)\vee(x\in B) y∈f(A∪B)⇒y=f(x),x∈A∪B⇒y=f(x),(x∈A)∨(x∈B)
⇒ ( y ∈ f ( A ) ) ∨ ( y ∈ f ( B ) ) ⇒ y ∈ f ( A ) ∪ f ( B ) \Rightarrow (y\in f(A))\vee(y\in f(B))\Rightarrow y\in f(A)\cup f(B) ⇒(y∈f(A))∨(y∈f(B))⇒y∈f(A)∪f(B)
如果 A ′ A' A′ 与 B ′ B' B′ 都是 Y Y Y 的子集,则
e) ( A ′ ⊂ B ′ ) ⇒ ( f − 1 ( A ′ ) ⊂ f − 1 ( B ′ ) ) (A'\subset B')\Rightarrow (f^{-1}(A')\subset f^{-1}(B')) (A′⊂B′)⇒(f−1(A′)⊂f−1(B′))
证明:
假设 A ′ ⊂ B ′ A'\subset B' A′⊂B′ 成立 .
若 f − 1 ( A ′ ) = ∅ f^{-1}(A')=\varnothing f−1(A′)=∅ , 则显然有 ( f − 1 ( A ′ ) ⊂ f − 1 ( B ′ ) ) (f^{-1}(A')\subset f^{-1}(B')) (f−1(A′)⊂f−1(B′))
若 f − 1 ( A ′ ) ≠ ∅ f^{-1}(A')\neq\varnothing f−1(A′)=∅ , 则存在 x ∈ f − 1 ( A ′ ) ⇒ y = f ( x ) , y ∈ A ′ ⇒ y = f ( x ) , y ∈ B ′ ⇒ x ∈ f − 1 ( B ′ ) x\in f^{-1}(A')\Rightarrow y=f(x),y\in A'\Rightarrow y=f(x),y\in B'\Rightarrow x\in f^{-1}(B') x∈f−1(A′)⇒y=f(x),y∈A′⇒y=f(x),y∈B′⇒x∈f−1(B′)
f) f − 1 ( A ′ ∩ B ′ ) = f − 1 ( A ) ∩ f − 1 ( B ) f^{-1}(A'\cap B')=f^{-1}(A)\cap f^{-1}(B) f−1(A′∩B′)=f−1(A)∩f−1(B)
证明:
若 f − 1 ( A ′ ∩ B ′ ) = ∅ f^{-1}(A'\cap B')=\varnothing f−1(A′∩B′)=∅ ,假定 f − 1 ( A ) ∩ f − 1 ( B ) ≠ ∅ f^{-1}(A)\cap f^{-1}(B)\neq \varnothing f−1(A)∩f−1(B)=∅,
则存在 x ∈ f − 1 ( A ) ∩ f − 1 ( B ) ⇒ ( y = f ( x ) ∈ A ′ ) ∧ ( y = f ( x ) ∈ B ′ ) x\in f^{-1}(A)\cap f^{-1}(B)\Rightarrow (y=f(x)\in A')\wedge(y=f(x)\in B') x∈f−1(A)∩f−1(B)⇒(y=f(x)∈A′)∧(y=f(x)∈B′)
⇒ y ∈ A ′ ∩ B ′ ⇒ x ∈ f − 1 ( A ′ ∩ B ′ ) \Rightarrow y\in A'\cap B'\Rightarrow x\in f^{-1}(A'\cap B') ⇒y∈A′∩B′⇒x∈f−1(A′∩B′) .
产生矛盾. 故 f − 1 ( A ) ∩ f − 1 ( B ) = ∅ = f − 1 ( A ′ ∩ B ′ ) f^{-1}(A)\cap f^{-1}(B)= \varnothing=f^{-1}(A'\cap B') f−1(A)∩f−1(B)=∅=f−1(A′∩B′)
若 f − 1 ( A ′ ∩ B ′ ) ≠ ∅ f^{-1}(A'\cap B')\neq \varnothing f−1(A′∩B′)=∅ , 则存在 x ∈ f − 1 ( A ′ ∩ B ′ ) ⇔ y = f ( x ) , y ∈ A ′ ∩ B ′ x\in f^{-1}(A'\cap B')\Leftrightarrow y=f(x),y\in A'\cap B' x∈f−1(A′∩B′)⇔y=f(x),y∈A′∩B′
⇔ x ∈ f − 1 ( A ) ∩ f − 1 ( B ) \Leftrightarrow x\in f^{-1}(A)\cap f^{-1}(B) ⇔x∈f−1(A)∩f−1(B)
g) f − 1 ( A ′ ∪ B ′ ) = f − 1 ( A ) ∪ f − 1 ( B ) f^{-1}(A'\cup B')=f^{-1}(A)\cup f^{-1}(B) f−1(A′∪B′)=f−1(A)∪f−1(B)
证明:
类似 f)
如果 B ′ ⊂ A ′ ⊂ Y B'\subset A'\subset Y B′⊂A′⊂Y , 则
h) f − 1 ( A ′ − B ′ ) = f − 1 ( A ′ ) − f − 1 ( B ′ ) f^{-1}(A'-B')=f^{-1}(A')-f^{-1}(B') f−1(A′−B′)=f−1(A′)−f−1(B′)
证明:
若 f − 1 ( A ′ − B ′ ) = ∅ f^{-1}(A'-B')=\varnothing f−1(A′−B′)=∅ , 假定 f − 1 ( A ′ ) − f − 1 ( B ′ ) f^{-1}(A')-f^{-1}(B') f−1(A′)−f−1(B′) 不为空集,
则存在 ( x ∈ f − 1 ( A ′ ) ) ∩ ( x ∉ f − 1 ( B ′ ) ) ⇒ y = f ( x ) , ( y ∈ A ′ ) ∧ ( y ∉ B ′ ) (x\in f^{-1}(A'))\cap(x\notin f^{-1}(B'))\Rightarrow y=f(x),(y\in A')\wedge(y\notin B') (x∈f−1(A′))∩(x∈/f−1(B′))⇒y=f(x),(y∈A′)∧(y∈/B′)
⇒ y = f ( x ) , y ∈ A ′ − B ′ \Rightarrow y=f(x),y\in A'-B' ⇒y=f(x),y∈A′−B′ . 产生矛盾. 故 f − 1 ( A ′ − B ′ ) = f − 1 ( A ′ ) − f − 1 ( B ′ ) = ∅ f^{-1}(A'-B')=f^{-1}(A')-f^{-1}(B')=\varnothing f−1(A′−B′)=f−1(A′)−f−1(B′)=∅ .
若 f − 1 ( A ′ − B ′ ) ≠ ∅ f^{-1}(A'-B')\neq\varnothing f−1(A′−B′)=∅ , 则存在 x ∈ f − 1 ( A ′ − B ′ ) x\in f^{-1}(A'-B') x∈f−1(A′−B′)
⇔ y = f ( x ) , x ∈ A ′ − B ′ ⇔ y = f ( x ) , ( y ∈ A ′ ) ∧ ( y ∉ B ′ ) \Leftrightarrow y=f(x),x\in A'-B' \Leftrightarrow y=f(x),(y\in A')\wedge(y\notin B') ⇔y=f(x),x∈A′−B′⇔y=f(x),(y∈A′)∧(y∈/B′)
⇔ ( x ∈ f − 1 ( A ′ ) ) ∧ ( x ∉ f − 1 ( B ′ ) ) ⇔ x ∈ f − 1 ( A ′ ) − f − 1 ( B ′ ) \Leftrightarrow (x\in f^{-1}(A'))\wedge(x\notin f^{-1}(B')) \Leftrightarrow x\in f^{-1}(A')-f^{-1}(B') ⇔(x∈f−1(A′))∧(x∈/f−1(B′))⇔x∈f−1(A′)−f−1(B′)
i) f − 1 ( C Y A ′ ) = C X f − 1 ( A ′ ) f^{-1}(C_YA')=C_Xf^{-1}(A') f−1(CYA′)=CXf−1(A′)
证明:
由 h) 可推得
对于任何集合 A ⊂ X A\subset X A⊂X 及任何集合 B ′ ⊂ Y B'\subset Y B′⊂Y,有
j) A ⊂ f − 1 ( f ( A ) ) A\subset f^{-1}(f(A)) A⊂f−1(f(A))
证明:
若 A = ∅ A=\varnothing A=∅ ,明显有 A ⊂ f − 1 ( f ( A ) ) A\subset f^{-1}(f(A)) A⊂f−1(f(A)) .
若 A ≠ ∅ A\neq\varnothing A=∅ , x ∈ A ⇒ f ( x ) ∈ f ( A ) ⇒ x ∈ f − 1 ( f ( A ) ) x\in A \Rightarrow f(x)\in f(A) \Rightarrow x\in f^{-1}(f(A)) x∈A⇒f(x)∈f(A)⇒x∈f−1(f(A))
k) f ( f − 1 ( B ′ ) ) ⊂ B ′ f(f^{-1}(B'))\subset B' f(f−1(B′))⊂B′
证明:
若 f ( f − 1 ( B ′ ) ) = ∅ f(f^{-1}(B'))=\varnothing f(f−1(B′))=∅ , 明显有 f ( f − 1 ( B ′ ) ) ⊂ B ′ f(f^{-1}(B'))\subset B' f(f−1(B′))⊂B′ .
若 f ( f − 1 ( B ′ ) ) ≠ ∅ f(f^{-1}(B'))\neq\varnothing f(f−1(B′))=∅ , y ∈ f ( f − 1 ( B ′ ) ) ⇒ y = f ( x ) , x ∈ f − 1 ( B ′ ) ⇒ y ∈ B ′ y\in f(f^{-1}(B'))\Rightarrow y=f(x),x\in f^{-1}(B') \Rightarrow y\in B' y∈f(f−1(B′))⇒y=f(x),x∈f−1(B′)⇒y∈B′
【4】满射和双射
a) f : X → Y f:X\to Y f:X→Y 是满射当且仅当 f ( f − 1 ( B ′ ) ) = B ′ f(f^{-1}(B'))=B' f(f−1(B′))=B′ 对任何集合 B ′ ⊂ Y B'\subset Y B′⊂Y 都成立
证明:
若 f : X → Y f:X\to Y f:X→Y 是满射,则 f ( X ) = Y f(X)=Y f(X)=Y . 则对于任何非空 B ′ ⊂ Y B'\subset Y B′⊂Y , f − 1 ( B ) ≠ ∅ f^{-1}(B)\neq \varnothing f−1(B)=∅ .
根据 【映射中的子集】k)可知 f ( f − 1 ( B ′ ) ) ⊂ B ′ f(f^{-1}(B'))\subset B' f(f−1(B′))⊂B′
若 B ′ = ∅ B'=\varnothing B′=∅ , 明显有 B ′ ⊂ f ( f − 1 ( B ′ ) ) B'\subset f(f^{-1}(B')) B′⊂f(f−1(B′)) .
若 B ′ ≠ ∅ B'\neq \varnothing B′=∅ , 则存在 y ∈ B ′ ⇒ y = f ( x ) , x ∈ f − 1 ( B ′ ) ⇒ y ∈ f ( f − 1 ( B ′ ) ) y\in B'\Rightarrow y=f(x),x\in f^{-1}(B')\Rightarrow y\in f(f^{-1}(B')) y∈B′⇒y=f(x),x∈f−1(B′)⇒y∈f(f−1(B′)) .
若 f ( f − 1 ( B ′ ) ) = B ′ f(f^{-1}(B'))=B' f(f−1(B′))=B′ 对任何集合 B ′ ⊂ Y B'\subset Y B′⊂Y 都成立 .
取 B ′ = Y B'=Y B′=Y , 则 f ( f − 1 ( Y ) ) = f ( X ) = Y f(f^{-1}(Y))=f(X)=Y f(f−1(Y))=f(X)=Y , 故 f f f 是满射.
b) f : X → Y f:X\to Y f:X→Y 是双射当且仅当 ( f − 1 ( f ( A ) ) = A ) ∧ ( f ( f − 1 ( B ′ ) ) = B ′ ) (f^{-1}(f(A))=A)\wedge(f(f^{-1}(B'))=B') (f−1(f(A))=A)∧(f(f−1(B′))=B′) 对任何集合 A ⊂ X A\subset X A⊂X 及 B ′ ⊂ Y B'\subset Y B′⊂Y 都成立.
证明:
由 a) 知 f ( f − 1 ( B ′ ) ) = B ′ ⇒ f 是满射 f(f^{-1}(B'))=B'\Rightarrow f 是满射 f(f−1(B′))=B′⇒f是满射 .
假设对任何 A ⊂ X A\subset X A⊂X 有 f − 1 ( f ( A ) ) = A f^{-1}(f(A))=A f−1(f(A))=A 成立 .
f ( x 1 ) = f ( x 2 ) ⇒ x 1 ∈ f − 1 ( f ( x 2 ) ) = { x 2 } ⇒ x 1 = x 2 f(x_1)=f(x_2)\Rightarrow x_1\in f^{-1}(f(x_2))=\{x_2\} \Rightarrow x_1=x_2 f(x1)=f(x2)⇒x1∈f−1(f(x2))={x2}⇒x1=x2
故 f f f 是单射 . 综合起来 , ( f − 1 ( f ( A ) ) = A ) ∧ ( f ( f − 1 ( B ′ ) = B ′ ) ) ⇒ f 是双射 (f^{-1}(f(A))=A)\wedge(f(f^{-1}(B')=B'))\Rightarrow f是双射 (f−1(f(A))=A)∧(f(f−1(B′)=B′))⇒f是双射 .
由 a)得 f 是满射 ⇒ f ( f − 1 ( B ′ ) ) = B ′ f是满射 \Rightarrow f(f^{-1}(B'))=B' f是满射⇒f(f−1(B′))=B′
若 f f f 还是单射 ,则
由【映射中的子集】j) 得 A ⊂ f − 1 ( f ( A ) ) A\subset f^{-1}(f(A)) A⊂f−1(f(A)) .
若 f − 1 ( f ( A ) ) = ∅ f^{-1}(f(A))=\varnothing f−1(f(A))=∅ , 明显有 f − 1 ( f ( A ) ) ⊂ A f^{-1}(f(A))\subset A f−1(f(A))⊂A
若 f − 1 ( f ( A ) ) ≠ ∅ f^{-1}(f(A))\neq \varnothing f−1(f(A))=∅ , 则存在 x ∈ f − 1 ( f ( A ) ) ⇒ f ( x ) ∈ f ( A ) x\in f^{-1}(f(A)) \Rightarrow f(x)\in f(A) x∈f−1(f(A))⇒f(x)∈f(A)
假设 x ∉ A x\notin A x∈/A , 则存在 x 0 ∈ A , f ( x 0 ) = f ( x ) ⇒ x = x 0 x_0\in A,f(x_0)=f(x)\Rightarrow x=x_0 x0∈A,f(x0)=f(x)⇒x=x0
产生矛盾. 故 x ∈ A x\in A x∈A . f − 1 ( f ( A ) ) ⊂ A f^{-1}(f(A)) \subset A f−1(f(A))⊂A
【5】单射
请证明以下命题等价:
a) f f f 是单射
b) 对于任何集合 A ⊂ X A\subset X A⊂X , 都有 f − 1 ( f ( A ) ) = A f^{-1}(f(A))=A f−1(f(A))=A
c) 对于 X X X 的任何子集 A , B A,B A,B ,都有 f ( A ∩ B ) = f ( A ) ∩ f ( B ) f(A\cap B)=f(A)\cap f(B) f(A∩B)=f(A)∩f(B)
d) f ( A ) ∩ f ( B ) = ∅ ⇔ A ∩ B = ∅ f(A)\cap f(B)=\varnothing \Leftrightarrow A\cap B=\varnothing f(A)∩f(B)=∅⇔A∩B=∅
e) 如果 B ⊂ A ⊂ X B\subset A\subset X B⊂A⊂X ,则 f ( A − B ) = f ( A ) − f ( B ) f(A-B)=f(A)-f(B) f(A−B)=f(A)−f(B)
证明:
a → \to → b ) 由【满射和双射】 b) 得
b → \to → c ) 取 A = ∅ A=\varnothing A=∅ , 则 f − 1 ( f ( ∅ ) ) = f − 1 ( ∅ ) = ∅ f^{-1}(f(\varnothing))=f^{-1}(\varnothing)=\varnothing f−1(f(∅))=f−1(∅)=∅
由 【映射中的子集】 c) 知 f ( A ∩ B ) ⊂ f ( A ) ∩ f ( B ) f(A\cap B)\subset f(A)\cap f(B) f(A∩B)⊂f(A)∩f(B) .
若 f ( A ) ∩ f ( B ) = ∅ f(A)\cap f(B)=\varnothing f(A)∩f(B)=∅ , 则 f ( A ) ∩ f ( B ) ⊂ f ( A ∩ B ) f(A)\cap f(B)\subset f(A\cap B) f(A)∩f(B)⊂f(A∩B)
若 f ( A ) ∩ f ( B ) ≠ ∅ f(A)\cap f(B)\neq \varnothing f(A)∩f(B)=∅ , 则 存在 y ∈ f ( A ) ∩ f ( B ) y\in f(A)\cap f(B) y∈f(A)∩f(B)
若存在 x 1 ∈ A ≠ x 2 ∈ B , f ( x 1 ) = f ( x 2 ) ⇒ x 2 ∈ f − 1 ( f ( x 1 ) ) x_1\in A\neq x_2\in B,f(x_1)=f(x_2)\Rightarrow x_2\in f^{-1}(f(x_1)) x1∈A=x2∈B,f(x1)=f(x2)⇒x2∈f−1(f(x1)) ,
这与 f − 1 ( f ( x 1 ) ) = x 1 f^{-1}(f(x_1))=x_1 f−1(f(x1))=x1 矛盾.
故只能存在 x ∈ A ∩ B , y = f ( x ) ⇒ y ∈ f ( A ∩ B ) x\in A\cap B,y=f(x) \Rightarrow y\in f(A\cap B) x∈A∩B,y=f(x)⇒y∈f(A∩B) . f ( A ) ∩ f ( B ) ⊂ f ( A ∩ B ) f(A)\cap f(B)\subset f(A\cap B) f(A)∩f(B)⊂f(A∩B)
c → \to → d ) f ( A ) ∩ f ( B ) = ∅ ⇔ f ( A ∩ B ) = ∅ ⇔ A ∩ B = ∅ f(A)\cap f(B)=\varnothing \Leftrightarrow f(A\cap B)=\varnothing \Leftrightarrow A\cap B=\varnothing f(A)∩f(B)=∅⇔f(A∩B)=∅⇔A∩B=∅
d → \to → e ) ( A − B ) ∩ B = ∅ ⇒ f ( A − B ) ∩ f ( B ) = ∅ (A-B)\cap B=\varnothing \Rightarrow f(A-B)\cap f(B)=\varnothing (A−B)∩B=∅⇒f(A−B)∩f(B)=∅
f ( A − B ) = ∅ ⇔ A − B = ∅ ⇔ A = B ⇔ f ( A ) − f ( B ) = ∅ f(A-B)=\varnothing\Leftrightarrow A-B=\varnothing \Leftrightarrow A=B\Leftrightarrow f(A)-f(B)=\varnothing f(A−B)=∅⇔A−B=∅⇔A=B⇔f(A)−f(B)=∅ .
f ( A − B ) ≠ ∅ ⇔ 存在 y ∈ f ( A − B ) ⇔ y = f ( x ) , x ∈ A − B ⇔ y ∈ ( f ( A ) − f ( B ) ) f(A-B)\neq \varnothing\Leftrightarrow 存在 y\in f(A-B)\Leftrightarrow y=f(x),x\in A-B \Leftrightarrow y\in (f(A)-f(B)) f(A−B)=∅⇔存在y∈f(A−B)⇔y=f(x),x∈A−B⇔y∈(f(A)−f(B))
e → \to → a )设有 f ( x 1 ) = f ( x 2 ) f(x_1)=f(x_2) f(x1)=f(x2) . 假设 x 1 ≠ x 2 x_1\neq x_2 x1=x2 , 取 B = { x 1 } , A = { x 1 , x 2 } B=\{x_1\},A=\{x_1,x_2\} B={x1},A={x1,x2}
则有 f ( A − B ) = f ( { x 2 } ) = f ( { x 1 , x 2 } ) − f ( { x 1 } ) = ∅ f(A-B)=f(\{x_2\})=f(\{x_1,x_2\})-f(\{x_1\})=\varnothing f(A−B)=f({x2})=f({x1,x2})−f({x1})=∅ . 产生矛盾 .
故 x 1 = x 2 x_1=x_2 x1=x2 . f f f 为单射 .
【6】逆映射
a) 如果映射 f : X → Y f:X\to Y f:X→Y 与 g : Y → X g:Y\to X g:Y→X 满足 g ∘ f = e X g\circ f=e_X g∘f=eX,则称 g g g 为 f f f 的左逆映射, f f f 为 g g g 的右逆映射.
证明:可能存在多个单侧逆映射(这与逆映射的唯一性不同)
证明:
映射 ( x , y ) ↦ g y (x,y)\overset{g}\mapsto y (x,y)↦gy , 有无数个右逆映射 y ↦ f a ( a , y ) y\overset{f_a}\mapsto(a,y) y↦fa(a,y) .
b) 设映射 f : X → Y f:X\to Y f:X→Y 与 g : Y → Z g:Y\to Z g:Y→Z 是双射 . 证明: g ∘ f : X → Z g\circ f:X\to Z g∘f:X→Z 是双射,并且 ( g ∘ f ) − 1 = f − 1 ∘ g − 1 (g\circ f)^{-1}=f^{-1}\circ g^{-1} (g∘f)−1=f−1∘g−1
证明:
x x x 与 y = f ( x ) y=f(x) y=f(x) 与 z = g ( y ) z=g(y) z=g(y) 一一对应. 则 x x x 与 z = g ( f ( x ) ) z=g(f(x)) z=g(f(x)) 一一对应.
( g ∘ f ) − 1 ( z ) = x (g\circ f)^{-1}(z)=x (g∘f)−1(z)=x .
( f − 1 ∘ g − 1 ) ( z ) = f − 1 ( g − 1 ( z ) ) = f − 1 ( y ) = x (f^{-1}\circ g^{-1})(z)=f^{-1}(g^{-1}(z))=f^{-1}(y)=x (f−1∘g−1)(z)=f−1(g−1(z))=f−1(y)=x
c) 证明: ( g ∘ f ) − 1 ( C ) = f − 1 ( g − 1 ( C ) ) (g\circ f)^{-1}(C)=f^{-1}(g^{-1}(C)) (g∘f)−1(C)=f−1(g−1(C)) 对于任何映射 f : X → Y f:X\to Y f:X→Y 与 g : Y → Z g:Y\to Z g:Y→Z 和任何集合 C ⊂ Z C\subset Z C⊂Z 都成立.
证明:
若 ( g ∘ f ) − 1 ( C ) = ∅ (g\circ f)^{-1}(C)=\varnothing (g∘f)−1(C)=∅ , 假设 f − 1 ( g − 1 ( C ) ) ≠ ∅ f^{-1}(g^{-1}(C))\neq \varnothing f−1(g−1(C))=∅ , 则存在 y ∈ Y y\in Y y∈Y , 使得 z = g ( y ) ∈ Z z=g(y)\in Z z=g(y)∈Z , 存在 x ∈ X x\in X x∈X ,使得 y = f ( x ) y=f(x) y=f(x) . 而 f − 1 ( g − 1 ( x ) ) = z f^{-1}(g^{-1}(x))=z f−1(g−1(x))=z . 这与 ( g ∘ f ) − 1 ( C ) = ∅ (g\circ f)^{-1}(C)=\varnothing (g∘f)−1(C)=∅ 矛盾 . 故 f − 1 ( g − 1 ( C ) ) ≠ ∅ f^{-1}(g^{-1}(C))\neq \varnothing f−1(g−1(C))=∅ .
若 ( g ∘ f ) − 1 ( C ) ≠ ∅ (g\circ f)^{-1}(C)\neq\varnothing (g∘f)−1(C)=∅ , 则存在 x ∈ ( g ∘ f ) − 1 ( C ) x\in (g\circ f)^{-1}(C) x∈(g∘f)−1(C) 使得 ( g ∘ f ) ( x ) = z ∈ C ⇒ g ( f ( x ) ) = z , y = f ( x ) ⇒ x ∈ f − 1 ( g − 1 ( z ) ) (g\circ f)(x)=z\in C \Rightarrow g(f(x))=z,y=f(x)\Rightarrow x\in f^{-1}(g^{-1}(z)) (g∘f)(x)=z∈C⇒g(f(x))=z,y=f(x)⇒x∈f−1(g−1(z)) . 故 x ∈ f − 1 ( g − 1 ( C ) ) x\in f^{-1}(g^{-1}(C)) x∈f−1(g−1(C)) .
d) 证明:由 ( x , y ) ↦ ( y , x ) (x,y)\mapsto (y,x) (x,y)↦(y,x) 给出的映射 F : X × Y → Y × X F:X\times Y\to Y\times X F:X×Y→Y×X 是双射. 试描述互逆映射 f : X → Y f:X\to Y f:X→Y 与 f − 1 : Y → X f^{-1}:Y\to X f−1:Y→X 的图像之间的相互联系
证明:
显然是双射 .
横纵坐标互换,关于 y = x y=x y=x 对称.
【7】图像
a) 证明:对于任何映射 f : X → Y f:X\to Y f:X→Y , 由 x ↦ F ( x , f ( x ) ) x\overset{F}\mapsto (x,f(x)) x↦F(x,f(x)) 定义的映射 F : X → X × Y F:X\to X\times Y F:X→X×Y 是单射.
证明:
设 ( x 1 , f ( x 1 ) ) = ( x 2 , f ( x 2 ) ) (x_1,f(x_1))=(x_2,f(x_2)) (x1,f(x1))=(x2,f(x2)) , 则 x 1 = x 2 x_1=x_2 x1=x2
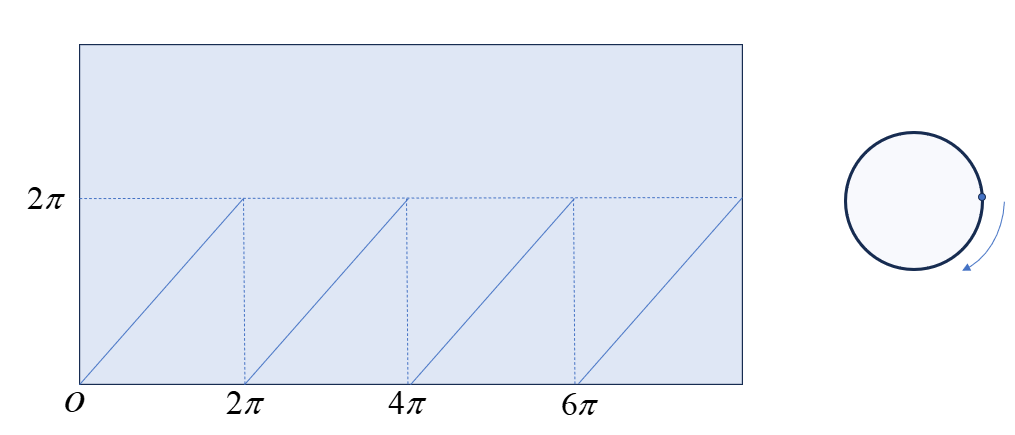
b) 设质点沿圆周 Y Y Y 匀速运动, X X X 是时间轴, x ↦ f y x\overset{f}\mapsto y x↦fy 是时刻 x ∈ X x\in X x∈X 与质点位置 y = f ( x ) ∈ Y y=f(x)\in Y y=f(x)∈Y 之间的对应关系. 请画出函数 f : X → Y f:X\to Y f:X→Y 在 X × Y X\times Y X×Y 上的图像
解:
设圆周 Y Y Y 长 2 π 2\pi 2π , 以某点 O O O 为原点,用一个非负数 y ∈ Y ⊂ R + y\in Y\subset \mathbb{R}^+ y∈Y⊂R+ 代表所处位置 , 设质点速度为 1
则图像为:
【8】实例再现
a) 对于之前提到的实例,说明其中的映射的类型
解:
圆的周长公式和球的体积公式:双射
光速的常数映射:既非单射又非满射
伽利略变换与一维洛伦兹变换:双射
投影映射:满射
补集:双射
特征函数:既非单射又非满射
泛函:满射
测地线:既非单射又非满射
平移算子:双射
质点系统:既非单射又非满射
势能:既非单射又非满射
机械能:既非单射又非满射
b) 欧姆定律 I = V R I=\frac{V}{R} I=RV 给出导体中的电流 I I I 与导体两端电压 V V V 和导体电阻 R R R 之间的联系. 请指出,哪些集合的映射 O : X → Y O:X\to Y O:X→Y 与欧姆定律相对应?欧姆定律所对应的关系是哪一个集合的子集?
解:
设电压可有正有负,电阻非负 . 即 V ∈ R , R ∈ R + V\in \mathbb{R},R\in\mathbb{R}^+ V∈R,R∈R+ .
则 O : R × R + → R O:\mathbb{R}\times \mathbb{R}^+\to \mathbb{R} O:R×R+→R .
欧姆定律对应的关系是 R × R + × R \mathbb{R}\times \mathbb{R}^+\times \mathbb{R} R×R+×R 的子集 .
c) 请求出伽利略变换与洛伦兹变换的逆变换 G − 1 G^{-1} G−1 , L − 1 L^{-1} L−1
解:
{ x ′ = x − v t t ′ = t ⇔ { x = x ′ + v t t = t ′ \begin{cases}x'=x-vt \\ t' = t\end{cases} \Leftrightarrow \begin{cases}x=x'+vt \\ t = t'\end{cases} {x′=x−vtt′=t⇔{x=x′+vtt=t′ . 这确定了 G − 1 G^{-1} G−1 .
{ x ′ = x − v t 1 − ( v c ) 2 t ′ = t − ( v c 2 ) x 1 − ( v c ) 2 ⇔ { ( v c 2 ) x ′ = ( v c 2 ) x − ( v c ) 2 t 1 − ( v c ) 2 v t ′ = v t − ( v c ) 2 x 1 − ( v c ) 2 ⇔ { x = x ′ + v t ′ 1 − ( v c 2 ) t = t ′ + ( v c 2 ) x ′ 1 − ( v c ) 2 \begin{cases}x'=\frac{x-vt}{\sqrt{1-(\frac{v}{c}})^2} \\ t' = \frac{t-(\frac{v}{c^2})x}{\sqrt{1-(\frac{v}{c}})^2}\end{cases} \Leftrightarrow \begin{cases}(\frac{v}{c^2})x'=\frac{(\frac{v}{c^2})x-(\frac{v}{c})^2t}{\sqrt{1-(\frac{v}{c}})^2} \\ vt' = \frac{vt-(\frac{v}{c})^2x}{\sqrt{1-(\frac{v}{c}})^2}\end{cases} \Leftrightarrow \begin{cases}x=\frac{x'+vt'}{\sqrt{1-(\frac{v}{c^2}})} \\ t = \frac{t'+(\frac{v}{c^2})x'}{\sqrt{1-(\frac{v}{c})^2}}\end{cases} ⎩ ⎨ ⎧x′=1−(cv)2x−vtt′=1−(cv)2t−(c2v)x⇔⎩ ⎨ ⎧(c2v)x′=1−(cv)2(c2v)x−(cv)2tvt′=1−(cv)2vt−(cv)2x⇔⎩ ⎨ ⎧x=1−(c2v)x′+vt′t=1−(cv)2t′+(c2v)x′ . 这确定了 L − 1 L^{-1} L−1 .
【9】稳定集、不变集、不动点
a) 对于映射 f : X → X f:X\to X f:X→X ,满足 f ( S ) ⊂ S f(S)\subset S f(S)⊂S 的集合 S ⊂ X S\subset X S⊂X 称为映射 f f f 的稳定集. 请写出平面沿其上给定向量的平移的稳定集.
解:
对于任意的 A ⊂ X A\subset X A⊂X , 作集合 S = { ( x + k a , y + k b ) ∣ ( x , y ) ∈ A , k ∈ R + } S=\{(x+ka,y+kb)|(x,y)\in A,k\in \mathbb{R}^+\} S={(x+ka,y+kb)∣(x,y)∈A,k∈R+} . 则 S S S 为平面沿其上给定向量 ( a , b ) (a,b) (a,b) 的平移的稳定集.
b) 对于映射 f : X → X f:X\to X f:X→X ,满足 f ( I ) = I f(I)=I f(I)=I 的集合 I ⊂ X I\subset X I⊂X 称为映射 f f f 的不变集. 请写出平面绕一个固定点的旋转的旋转不变集.
解: 对于任意的 A ⊂ X A\subset X A⊂X , 作集合 I = { ( m , n ) ∣ ( m − a ) 2 + ( n − b ) 2 = ( x − a ) 2 + ( y − b ) 2 , ( x , y ) ∈ A } I=\{(m,n)|(m-a)^2+(n-b)^2=(x-a)^2+(y-b)^2,(x,y)\in A\} I={(m,n)∣(m−a)2+(n−b)2=(x−a)2+(y−b)2,(x,y)∈A} . 则 I I I 为平面绕一个固定点 ( a , b ) (a,b) (a,b) 的旋转的旋转不变集.
c) 对于映射 f : X → X f:X\to X f:X→X ,满足 f ( p ) = p f(p)=p f(p)=p 的集合 p ∈ X p\in X p∈X 称为映射 f f f 的不动点. 证明:平面的平移、旋转和位似变换的任何复合在位似系数小于 1 时具有不动点.
证明:
本题有点难,征求大家的解答. 以下解答仅供参考.
姑且认为旋转中心和位似中心都是映射后的原点.
设平面为 P P P . 对于 x ∈ P x\in P x∈P , 相继作平移、旋转和位似变换后, x ′ = λ R x + b x'=\lambda Rx+b x′=λRx+b
其中, λ < 1 \lambda<1 λ<1 为位似系数, R R R 为旋转矩阵(行列式为1) , b b b 为平移向量作相同旋转和位似变换后生成的常数向量 .
解 x = λ R x + b x=\lambda Rx+b x=λRx+b 得唯一不动点 x = ( I − λ R ) − 1 b x=(I-\lambda R)^{-1}b x=(I−λR)−1b ( λ < 1 \lambda<1 λ<1 保证 I − λ R I-\lambda R I−λR 可逆)
d) 认为伽利略变换和洛伦兹变换是平面到自身上的映射,它把坐标为 ( x , t ) (x,t) (x,t) 的点变到坐标为 ( x ′ , t ′ ) (x',t') (x′,t′) 的点. 请求出这些变换的不变集.
解:
本题有点难,征求大家的解答. 以下解答仅供参考.
伽利略变换 { x ′ = x − v t t ′ = t \begin{cases}x'=x-vt \\ t' = t\end{cases} {x′=x−vtt′=t . 对于平面上任意一个子集 A A A , I = { ( x − k v t , t ) ∣ ( x , t ) ∈ A , k ∈ R + } I=\{(x-kvt,t)|(x,t)\in A,k\in\mathbb{R}^+\} I={(x−kvt,t)∣(x,t)∈A,k∈R+} 都是伽利略变换的不变集.
洛伦兹变换 { x ′ = x − v t 1 − ( v c ) 2 t ′ = t − ( v c 2 ) x 1 − ( v c ) 2 \begin{cases}x'=\frac{x-vt}{\sqrt{1-(\frac{v}{c}})^2} \\ t' = \frac{t-(\frac{v}{c^2})x}{\sqrt{1-(\frac{v}{c}})^2}\end{cases} ⎩ ⎨ ⎧x′=1−(cv)2x−vtt′=1−(cv)2t−(c2v)x . 对于平面上任意一个子集 A A A , I = { ( x − k v t , t − k v x ) ∣ ( x , t ) ∈ A , k ∈ R + } I=\{(x-kvt,t-kvx)|(x,t)\in A,k\in\mathbb{R}^+\} I={(x−kvt,t−kvx)∣(x,t)∈A,k∈R+} 都是伽利略变换的不变集.
【10】流体的定常流动
考虑流体的定常流动,即每个流动的点的速度不随时间变化. 位于空间点 x x x 处的流体点,在时间 t t t 内移动到某个新的空间点 f t ( x ) f_t(x) ft(x) , 从而形成流体所占空间的点的映射 x ↦ f t ( x ) x\mapsto f_t(x) x↦ft(x). 该映射与时间有关,称为时间 t t t 内的变换. 请证明: f t 2 ∘ f t 1 = f t 1 ∘ f t 2 = f t 1 + t 2 f_{t_2}\circ f_{t_1}=f_{t_1}\circ f_{t_2}=f_{t_1+t_2} ft2∘ft1=ft1∘ft2=ft1+t2 , f t ∘ f − t = f 0 = e X f_t\circ f_{-t}=f_0=e_X ft∘f−t=f0=eX .
证:
f t ( x ) = x + v t f_t(x)=x+vt ft(x)=x+vt
( f t 2 ∘ f t 1 ) ( x ) = f t 2 ( f t 1 ( x ) ) = f t 2 ( x + v t 1 ) = x + v t 1 + v t 2 = x + v ( t 1 + t 2 ) = f t 1 + t 2 ( x ) (f_{t_2}\circ f_{t_1})(x)=f_{t_2}(f_{t_1}(x))=f_{t_2}(x+vt_1)=x+vt_1+vt_2=x+v(t_1+t_2)=f_{t_1+t_2}(x) (ft2∘ft1)(x)=ft2(ft1(x))=ft2(x+vt1)=x+vt1+vt2=x+v(t1+t2)=ft1+t2(x)
( f t 1 ∘ f t 2 ) ( x ) = f t 1 ( f t 2 ( x ) ) = f t 1 ( x + v t 2 ) = x + v t 2 + v t 1 = x + v ( t 1 + t 2 ) = f t 1 + t 2 ( x ) (f_{t_1}\circ f_{t_2})(x)=f_{t_1}(f_{t_2}(x))=f_{t_1}(x+vt_2)=x+vt_2+vt_1=x+v(t_1+t_2)=f_{t_1+t_2}(x) (ft1∘ft2)(x)=ft1(ft2(x))=ft1(x+vt2)=x+vt2+vt1=x+v(t1+t2)=ft1+t2(x)
故 f t 2 ∘ f t 1 = f t 1 ∘ f t 2 = f t 1 + t 2 f_{t_2}\circ f_{t_1}=f_{t_1}\circ f_{t_2}=f_{t_1+t_2} ft2∘ft1=ft1∘ft2=ft1+t2 .
( f t ∘ f − t ) ( x ) = f t ( f − t ( x ) ) = f t ( x − v t ) = x − v t + v t = x = f 0 ( x ) = e X ( x ) (f_{t}\circ f_{-t})(x)=f_t(f_{-t}(x))=f_t(x-vt)=x-vt+vt=x=f_0(x)=e_X(x) (ft∘f−t)(x)=ft(f−t(x))=ft(x−vt)=x−vt+vt=x=f0(x)=eX(x)
故 f t ∘ f − t = f 0 = e X f_t\circ f_{-t}=f_0=e_X ft∘f−t=f0=eX .






















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








