乘法逆元【费马小定理+扩展欧几里得】

模运算性质

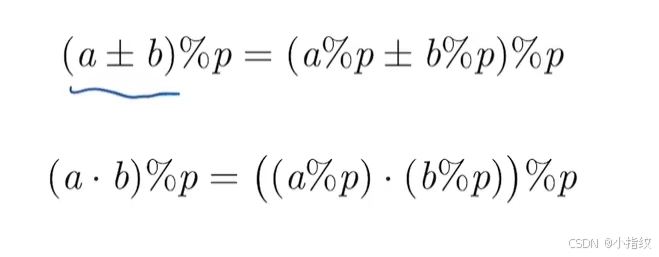
费马小定理

a,b互质：gcd(a,b)=1

乘法逆元

a,b互质,满足a*x同余1(mod b),x是a模b的乘法逆元，记作a的-1次方。

扩展欧几里得算法

求ax+by=gcd(a,b)的一组(x,y).

随机栈

题目来源：随机栈


解题思路
想算每次拿出数的概率，就需要知道每次拿的时候有几种选择，满足条件的选择有几种，需要记录下来桟里相同的数据有多少个，可以借助优先队列和map来写。
由于这道题要取模，运用到了乘法逆元。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod = 998244353;
map<int, int> m;
int pow1(int a, int b) 
{
	int res = 1;
	for (; b; b >>= 1) 
	{
		if (b & 1)res = res * a % mod;
		a = a * a % mod;
	}
	return res % mod;
}
signed  main() {
	priority_queue<int, vector<int>, greater<int> > p;//小顶堆
	int n, num, l = -1, t = 0, s = 1, x = 1;
 
	cin >> n;
	for (int i = 0; i < 2 * n; i++) 
	{
		cin >> num;

		if (t != 1)
		 {
			if (num == -1) 
			{
				s = s * m[p.top()] % mod;//分子，可以选择的数字
				x = x * p.size() % mod;//分母，队列里数字个数
				if (p.top() >= l) 
				{
					l = p.top();
					m[p.top()]--;
					p.pop();
				}
				else
					t = 1;
			} 
			else 
			{
				p.push(num);
				m[num]++;
			}
		}
	}
	if (t == 1)
		cout << "0" << endl;
	else 
	{
		int ans = s * pow1(x, mod - 2) % mod;//除法取模
		cout << ans << endl;
	}

}