二叉搜索判定树的创建

最新推荐文章于 2025-05-19 20:18:50 发布

氨基蝶呤

最新推荐文章于 2025-05-19 20:18:50 发布

阅读量899

点赞数 18

文章标签：算法

本文链接：https://blog.csdn.net/2402_89294789/article/details/148057829

版权

什么是二叉搜索判定树？

一颗二叉树，描述了在有序数组上执行二分查找时所有可能得搜索路径。

列如有序数组arr[5]={4,8,12,23,32}，要找到23,二分查找的示意图如下：

mid就是比较次数，成功查找的平均比较次数约为logn（底是2）

代码如下：

int BS(int e,int arr[],int &count,int low,int high){
   if(low<=high){
   int mid=(low+high)/2;
   if(e==arr[mid]) return mid;//找到的话就返回下标
   else if(e<arr[mid]){//要找的值比中间值小就更新high的值，再到左边这一半进行二分查找
       high=mid-1;
       return BS(e,arr,count,low,high);
   }
   else{
       low=mid+1;
       return BS(e,arr,count,low,high);
   }
   }
   return -1;//找不到就返回-1
}

要创建二叉搜索判定树，实际上就是模拟二分查找的路径。对与上例数组，其二叉搜索判定树如下：

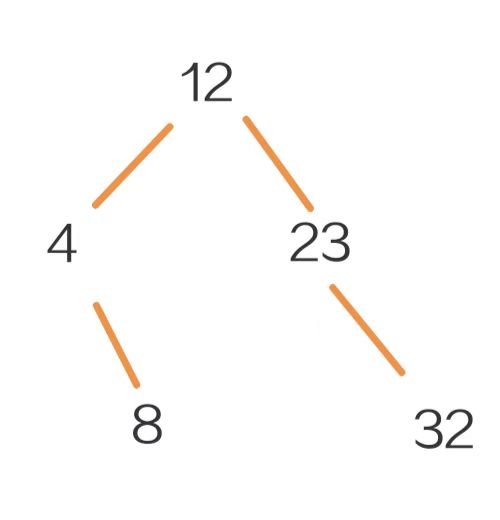
第一次比较：low=0,high=4,mid=2,arr[2]=12,所以根节点就是12

第二次比较：如果目标元素比12小就在左子树里搜索，此时high=mid-1=1,low=0,mid=0,arr[0]=4,左孩子就是4，每次要找比12小的元素都要先和12比较，再和4比较；每次要找比12大的元素都要先和12比较，再和23比较

以此类推，最多比较三次，就能得到出任何一个值在数组里查找的结果。

根据这个例子，可以看出二叉搜索判定树具有以下性质：

对于有n个元素的有序表，判定树的高度为[logn]+1
比较的最多次数为[logn]+1
对于查找失败的元素，最少比较次数为[logn]（找3,先和12比较再和4比较，两次就得出结果）

BSDT其实就是在BST(二叉搜索树)的基础上，更加靠近完全二叉树的树型，不会像BST那样会退化成链状结构，所以效率更高。

二叉树创建的关键代码如下，主要思想还是递归函数：

void CreatBST(BT &T,int arr[],int low,int high){
   if(low>high){
       T=NULL;
       return;
   }
   int mid=(low+high)/2;
   T=(BT)malloc(sizeof(BiTree));
   T->data=arr[mid];
   CreatBST(T->lchild,arr,low,mid-1);
   CreatBST(T->rchild,arr,mid+1,high);
}

传值调用low和high,一旦low>high就结束，否则将arr[mid]作为数的新结点，通过递归将数组创建结点的左子树(high的值以mid-1传入)和右子树 (low的值以mid+1传入)，这样就实现了BSDT的创建。

下面是完整代码：

#include <bits/stdc++.h>
#define max 10010
using namespace std;
typedef struct BiTree{
	int data;
	BiTree *rchild;
	BiTree *lchild;
}BiTree,*BT;
void CreatBST(BT &T,int arr[],int low,int high){
	if(low>high){
		T=NULL;
		return;
	}
	int mid=(low+high)/2;
	T=(BT)malloc(sizeof(BiTree));
	T->data=arr[mid];
	CreatBST(T->lchild,arr,low,mid-1);
	CreatBST(T->rchild,arr,mid+1,high);
}
void PreOrder(BT T){
	if(T){//先序遍历
		cout<<T->data<<" ";
		PreOrder(T->lchild);
		PreOrder(T->rchild);
	}
}
int main(){
	int n;
	cin>>n;
	int arr[max]={0};
	for(int i=0;i<n;i++){
		cin>>arr[i];
	}
	sort(arr,arr+n);
	n=unique(arr,arr+n)-arr;//删除重复元素后的元素个数
    cout<<n<<"\n";
    BT T;
    CreatBST(T,arr,0,n-1);
    PreOrder(T);
	return 0;
}

在主函数里面要先实现从小到大排序并且删除重复元素。

先序遍历输出的结果如下：