深度学习笔记（二）——Hyperparameter（补充）

原创已于 2025-10-12 09:38:31 修改 · 617 阅读

11 ·

CC 4.0 BY-SA版权

文章标签：

#笔记 #深度学习 #人工智能 #超参数 #正则化

于 2025-10-12 09:31:34 首次发布

深度学习笔记专栏收录该内容

2 篇文章

订阅专栏

引言

大家好，欢迎回到我的深度学习“炼丹”笔记！

在上一篇博客中，我们一起探讨了学习率 (Learning Rate) 和优化器 (Optimizer) 这两个在模型训练中至关重要的超参数。在正式开始下半场之前，我们先快速回顾一下上篇中几个非常实用的结论 (Takeaways)，这些观点对于理解后续内容也很有帮助：

别怕局部最优，警惕鞍点：在现代深度学习的高维空间中，我们真正需要克服的往往是鞍点 (Saddle Point)，而非理论上的局部最小值 (Local Minima)。像 Momentum 和 Adam 这样的自适应优化器，正是帮助我们穿越这些平坦区域的“越野车”。
Warm-up 并非万能药：它主要用于解决训练初期，由于参数随机初始化可能导致的梯度爆炸或模型振荡问题，特别是在使用大学习率或大 Batch Size 的场景下。如果你的训练过程很稳定，不加 Warm-up 也完全没问题。
AdamW 是新趋势：相比 Adam，AdamW 更好地解耦了 L2 正则化（即权重衰减）和梯度更新，在许多任务上表现更佳。当你不知道用什么优化器时，选用 AdamW 通常是个稳妥且优秀的选择。

好了，回顾结束！现在，让我们正式进入下半场，继续探索超参数世界里剩下的几位重要成员：

批量大小 (Batch Size)
训练轮数 (Epochs)
正则化策略：Dropout 与 L1/L2 正则化 (Weight Decay)
其他常见超参数

一、批量大小（Batch Size）与训练轮数（Epochs）

在确定了学习率和优化器这些“如何更新参数”的策略后，我们需要定义训练的“宏观结构”：我们打算如何给模型“喂”数据，以及总共要“喂”多久？ 这就引出了两个紧密相关的超参数：批量大小 (Batch Size) 和 训练轮数 (Epochs)。

打个比方，如果整个训练数据集是一本厚厚的教科书：

Batch Size 就是你一次读几页才停下来总结一下（进行一次参数更新）。
Epochs 就是你打算把整本教科书通读几遍。

显然，一次读的页数（Batch Size）会直接影响你读完整本书的速度，以及你对知识的吸收效果。

核心概念定义

首先，我们必须再次明确这三个概念：

Batch (批): 从总数据集中分出的一小批样本。
Iteration (迭代): 模型处理完一个 Batch，并完成一次参数更新的过程。
Epoch (轮): 模型完整地学习了一遍整个训练数据集的过程。

它们之间的关系是：一个 Epoch 包含的 Iteration 次数 = ⌈数据集总样本数 / Batch Size⌉ (向上取整)。

权衡的艺术：选择合适的 Batch Size

Batch Size 的选择，是一个在训练速度、硬件限制和模型泛化能力之间的经典权衡。

使用较大的 Batch Size
- 优点:
  1. 训练速度快：更能发挥 GPU 的并行计算能力，完成一个 Epoch 所需的迭代次数更少，总耗时更短。
  2. 梯度方向更稳定：每次更新都考虑了大量样本，计算出的梯度更能代表整个数据集的真实方向，使得损失函数下降的曲线更平滑。
- 缺点:
  1. 显存消耗巨大：这是最直接的物理限制，过大的 Batch Size 会导致“显存溢出 (Out of Memory)”。
  2. 可能损害泛化能力：由于梯度过于稳定，模型可能会被“猛推”到一个尖锐的最小值 (Sharp Minimum)。这种最小值在训练集上表现很好，但在测试集上可能表现不佳，因为它对输入的微小变化非常敏感。
使用较小的 Batch Size
- 优点:
  1. 硬件要求低：显存占用小，对普通设备更友好。
  2. 自带正则化效果：每次迭代的梯度都带有一定的随机性（噪声），这种“不稳定”反而像是在训练中不断给模型施加“扰动”，有助于模型跳出局部最优，最终找到一个更平坦的最小值 (Flat Minimum)。平坦的最小值通常意味着更好的泛化能力。

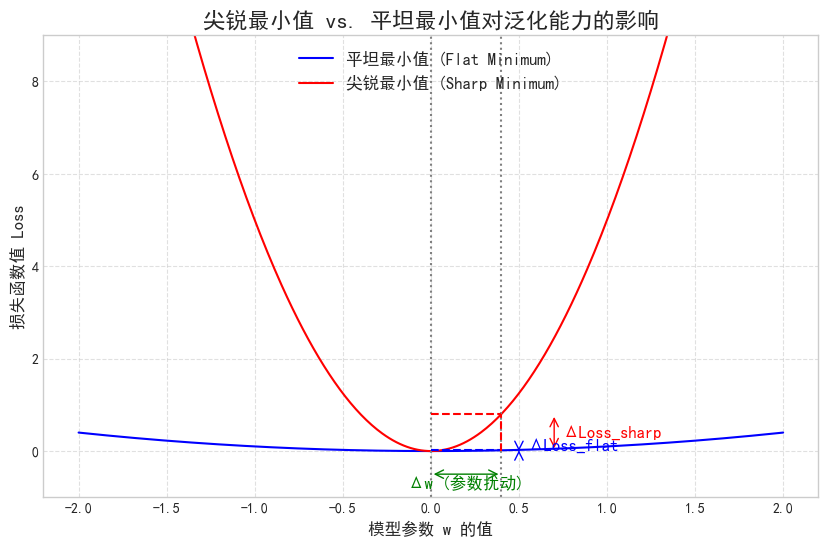
(图片使用numpy和matplotlib绘制得到）

缺点:
1. 训练总时间可能更长：虽然 GPU 利用率可能不高，但完成一个 Epoch 需要的迭代次数大大增加。
2. 损失函数震荡：训练过程会非常“颠簸”，需要配合一个较小的学习率来保证模型能够收敛。

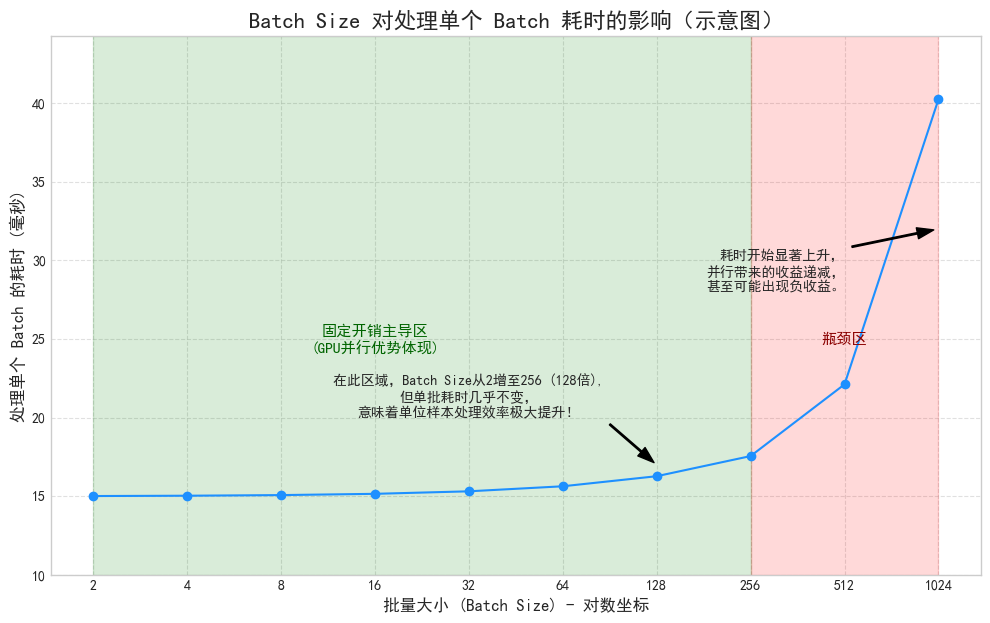
(图片使用numpy和matplotlib绘制得到）

Attention：为什么 Batch Size 通常是2的次幂？

将训练批次大小（Batch Size）设置为2的次幂（如32, 64, 128, 256）主要是为了最大化硬件（尤其是GPU）的计算和内存访问效率。

1. 硬件内存对齐 (Memory Alignment)

这是最核心、最底层的的原因。

计算机内存结构：CPU和GPU的内存是按块（Blocks/Chunks）来组织和访问的，而不是一个字节一个字节地零散访问。这些块的大小通常是2的次幂（例如，缓存行Cache Line通常是64字节）。
对齐访问 vs. 非对齐访问：当处理器需要读取数据时，如果数据的起始地址和大小都与这些内存块“对齐”，那么一次内存事务（Memory Transaction）就可以读取整个数据块，效率极高。如果数据没有对齐（例如，大小为33的数据跨越了两个内存块），处理器可能需要进行两次内存读取，然后将结果拼接起来，这会引入额外的开销和延迟。
形象的比喻：想象一下你去图书馆取书。书架上每格正好能放32本书。
- 对齐的情况 (Batch Size = 32)：你需要32本书，管理员直接把一整格的书推给你，非常快。
- 不对齐的情况 (Batch Size = 33)：你需要33本书，管理员需要先推给你一整格（32本），然后再去下一格，只为了拿出第33本书。这个“再去下一格”的操作就是额外开销。

将批次大小设置为2的次幂，可以确保数据在内存中能够更好地对齐，从而实现更快的内存读取和写入速度，这对于数据密集型的深度学习训练至关重要。

2. GPU并行计算架构 (CUDA Cores & Warps)

GPU通过大规模并行计算来加速训练，其执行单元的组织方式也偏爱2的次幂。

Warp/Wavefront：在NVIDIA的GPU中，线程（Threads）是以一个称为“Warp”的组来调度和执行的，一个Warp通常包含32个线程。在AMD的GPU中，类似的概念叫做“Wavefront”，通常是32或64个线程。
充分利用计算单元：GPU执行指令时，是一个Warp中的所有线程同时执行相同的指令，只是作用于不同的数据上（这被称为SIMT - Single Instruction, Multiple Threads）。
- 如果你的批次大小是64，那么GPU可以调度两个完整的Warp（2 * 32 = 64），所有64个线程都在进行有效的计算，硬件利用率是100%。
- 如果你的批次大小是33，GPU会调度两个Warp来处理。第一个Warp处理前32个样本，完全被利用。第二个Warp被启动，但它内部的32个线程中，只有1个线程在工作（处理第33个样本），其余31个线程都是空闲的，但它们仍然占用了计算资源。这就造成了巨大的硬件资源浪费。

因此，将批次大小设置为32的倍数（如32, 64, 128）可以确保GPU的计算单元得到最充分的利用，避免“线程闲置”造成的效率损失。

3. 专用硬件单元和底层库的优化

Tensor Cores：现代NVIDIA GPU（如Volta架构及之后）包含专门用于矩阵乘法和累加运算的硬件单元——Tensor Cores。这些单元被高度优化，它们处理的矩阵维度通常是8x8或16x16。为了让Tensor Cores发挥最大效能，输入的数据维度（包括批次大小）最好是8的倍数或16的倍数。2的次幂（≥8）自然满足这个条件。
cuDNN/oneMKL等加速库：像NVIDIA的cuDNN、Intel的oneMKL这样的底层深度学习加速库，内部包含了大量为特定硬件手写的、高度优化的计算“核函数”（Kernels）。这些库的开发者会优先为最常见、最高效的尺寸（通常是2的次幂）编写最优代码路径。当你使用这些尺寸时，库会调用最快的那个实现。如果使用一个“奇怪”的尺寸，库可能会回退到一个更通用、但速度较慢的算法。

恰到好处：如何确定训练的轮数 (Epochs)

知道了模型一次“吃”多少数据，下一个问题就是总共要“喂”几轮？Epochs 的数量直接决定了模型的拟合程度。

Epochs 过少：模型还没学透，处于欠拟合 (Underfitting) 状态。就像一个学生书都没看完就去考试，成绩自然很差。
Epochs 过多：模型把训练集“背”得滚瓜烂熟，连里面的错别字（噪声）都记住了，导致过拟合 (Overfitting)。虽然在模拟题（训练集）上能拿满分，但一到正式考试（测试集）就原形毕露。

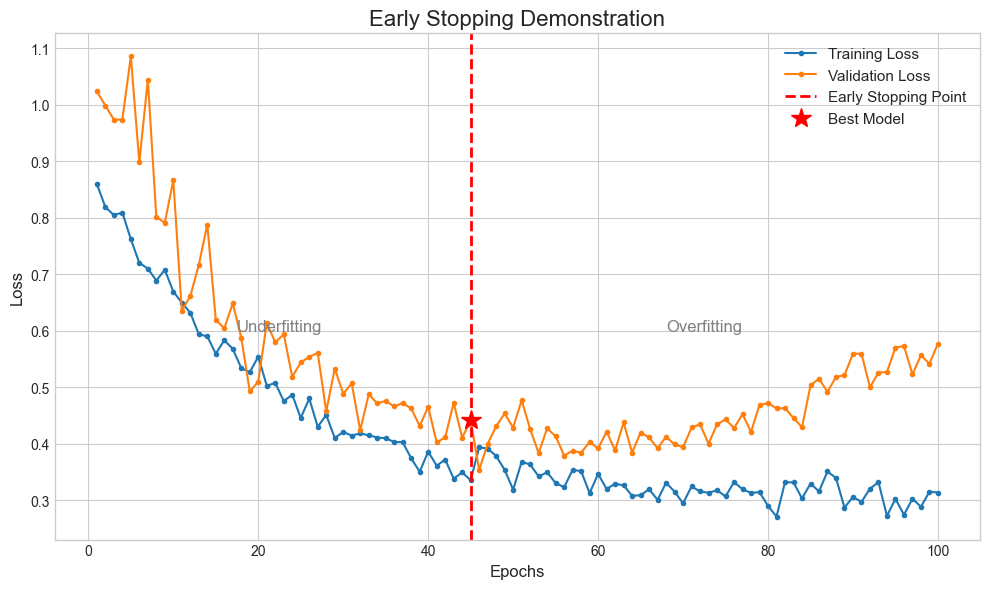
(图片使用numpy和matplotlib绘制得到）

那么，如何找到那个完美的“火候”呢？答案是：不要去猜，让模型自己告诉我们！

这就要用到深度学习实践中最重要的技巧之一：早停 (Early Stopping)。

早停的实施步骤：

划分验证集 (Validation Set): 从训练数据中预留一小部分（例如10-20%）作为验证集。它不参与梯度更新，只作为一个“模拟考场”，用来评估模型在每个 Epoch 结束后的真实水平。
持续监控：在每个 Epoch 训练结束后，我们都在验证集上计算模型的损失（Validation Loss）或准确率等指标。
找到“拐点”并停止：我们会观察到，在训练初期，训练损失和验证损失都会下降。但到某个点之后，训练损失仍在下降，而验证损失却停止下降，甚至开始回升。这个“拐点”就是模型开始过拟合的信号！此时，我们就应该立即停止训练，并保存验证损失最低时的那个模型作为最佳模型。

实践策略与总结

Batch Size 的选择:
- 在显存允许的范围内，从一个不大不小的值开始尝试（这通常与数据集的大小相关）。
- 选择 2 的幂次方 (32, 64, 128...) 通常能获得更好的硬件效率。
- 如果追求极致的泛化性能，可以尝试较小的 Batch Size，并耐心等待训练完成。如果追求训练速度，则在显存允许下尽可能增大 Batch Size，并配合适当的学习率调整。
Epochs 的确定:
- 不要预先固定一个很大的 Epochs 数。
- 使用 Early Stopping 配合验证集来动态地决定何时停止训练。这不仅能有效防止过拟合，还能在模型达到最佳性能时自动结束，节省大量时间和计算资源。

二、正则化策略 (Regularization)

到目前为止，我们讨论的超参数主要关注如何让模型“学得快、学得好”。但还有一个同样重要的问题：如何防止模型“学过头”？这就是过拟合 (Overfitting)。

一个过拟合的模型，就像一个只会死记硬背、不懂变通的学生。他在模拟题（训练集）上能考满分，因为他把所有题目的答案都背下来了；可一旦遇到题型稍有变化的新考题（测试集），他就束手无策。

正则化 (Regularization) 就是一套旨在防止过拟合、提升模型泛化能力 (Generalization) 的方法论。它的核心思想是对模型的复杂度进行限制或惩罚，迫使它去学习数据中更本质、更普适的规律，而不是去记那些无关紧要的细节和噪声。

下面我们来深入探讨几种最核心的正则化技术。

1. L1 & L2 正则化 (权重惩罚)

这是最经典的正则化方法。它通过修改损失函数，增加一个关于模型权重的“惩罚项”来实现。

标准的损失函数：

Loss = 数据损失 (Data Loss) (例如：均方误差)

加入正则化后的损失函数：

New Loss = 数据损失 (Data Loss) + λ * 惩罚项 (Penalty Term)

λ (Lambda)：正则化强度系数，是一个超参数。它控制着“惩罚”的力度。
- λ 越大，惩罚越重，模型越趋向于简单，可能导致欠拟合 (Underfitting)。
- λ 越小，惩罚越轻，模型越容易变得复杂，可能导致过拟合 (Overfitting)。

L2 正则化 (Ridge Regression / 岭回归)

工作原理:
它的惩罚项是模型所有权重 w 的平方和，再乘以一个超参数 λ (Lambda)。
L2 惩罚 = λ * Σ(w²)
直观理解:
L2 正則化不喜歡“极端”的权重。如果某个权重值特别大，它的平方就会变得非常大，导致惩罚项急剧增加。为了最小化整体损失，优化器就必须在“拟合训练数据”和“保持权重小”之间找到一个平衡。
- 为什么小权重能防止过拟合？ 一个权重很大的模型，通常意味着它对输入特征的微小变化非常敏感。这会导致模型的决策边界变得非常“陡峭”和“弯曲”，拼命去迎合每一个训练样本点，从而产生过拟合。相反，权重较小的模型，其决策边界会更平滑、更简单，对噪声不那么敏感，泛化能力也就更强。
- “权重衰减”之名: 在实际的梯度更新中，L2 正则化的效果等同于在每次更新权重时，先让权重自身“衰减”一点点 (w = w * (1 - decay_rate))，然后再进行常规的梯度下降。这便是“权重衰减 (Weight Decay)”这个名字的由来。
实践建议:
L2 正则化是深度学习中最常用、最默认的正则化选项。当你使用的优化器是 AdamW 时，其中的 "W" 就代表它正确地实现了权重衰减。你只需要设置 weight_decay 这个超参数（它就是 λ）即可，通常从 1e-4, 1e-3 等值开始尝试。

L1 正则化 (Lasso Regression)

工作原理:
它的惩罚项是模型所有权重 w 的绝对值之和。
L1 惩罚 = λ * Σ|w|
独特之处：稀疏性 (Sparsity):
L1 正则化有一个非常强大的副作用：它会促使很多不重要的权重精确地变为 0。这相当于在训练过程中自动进行“特征选择”，把那些对结果贡献不大的特征给“屏蔽”掉，从而得到一个稀疏模型。
- 几何解释: 想象一个二维的权重空间 (w1, w2)。L2 惩罚的等值线是一个圆形，而 L1 的等值线是一个菱形。当损失函数的等高线与这些惩罚项的等值线相切时（即找到最优解），L1 的菱形尖角更容易与坐标轴相交，从而导致某个权重恰好为 0。
实践建议:
在深度学习中，L1 正则化用得相对较少，因为 L2 的平滑效果通常更受欢迎。但在某些需要模型可解释性或希望压缩模型大小的场景下，L1 的稀疏特性会非常有价值。

2. Dropout (随机失活)

Dropout 是一种非常强大且思想清奇的正则化技术，专门为神经网络设计。

工作原理:
在模型训练的每一次前向传播中，Dropout 会以一个预设的概率 p (即 Dropout Rate)，随机地将网络中的一部分神经元“临时关闭”。这些被关闭的神经元既不参与前向计算，也不参与反向传播的梯度更新。在测试时候则恢复。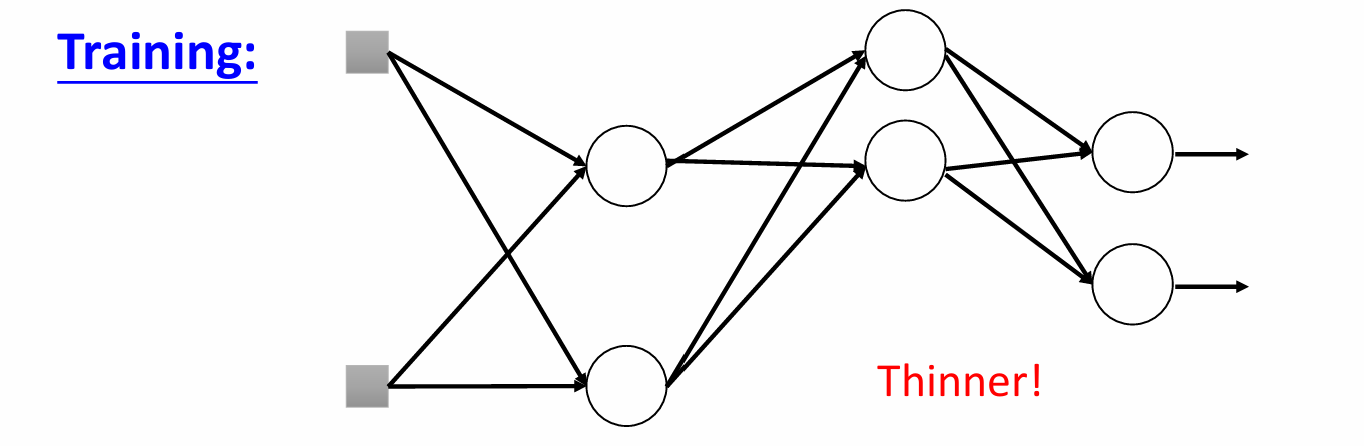

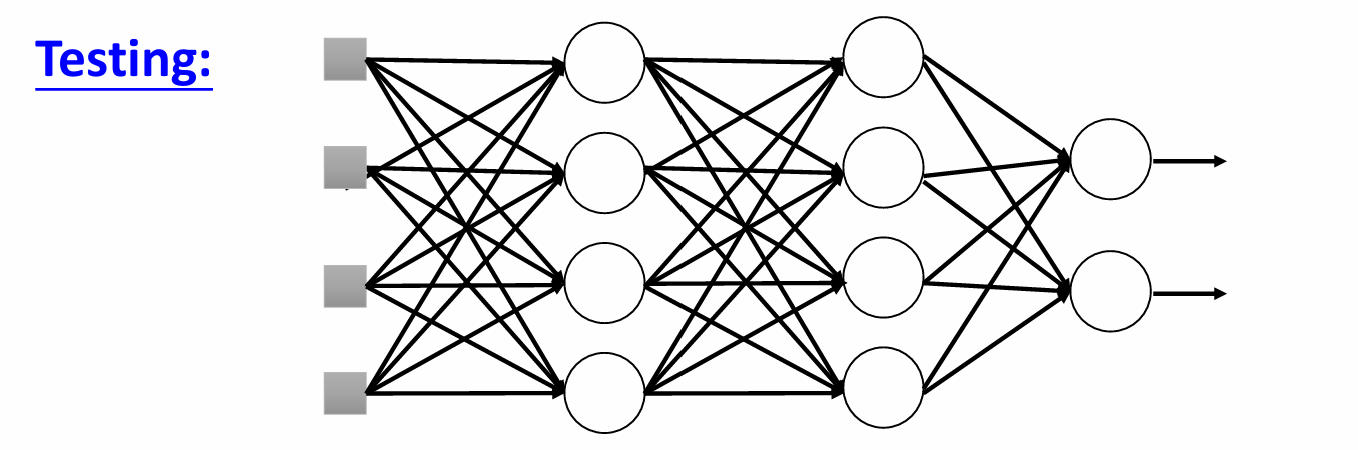
（这两张图片取自李宏毅老师课件，我觉得老师的例子可能更生动，下面这张图也来自老师课件）

这说明，搞科研和喜欢漫画并不冲突啊，魂淡！

为什么有效？
1. 打破“协同适应”: 如果没有 Dropout，网络中的神经元可能会产生复杂的依赖关系。比如，神经元 A 的输出可能高度依赖于神经元 B 和 C 的特定组合。这种“小团体”式的学习模式很脆弱，容易过拟合。Dropout 随机地让“队友”消失，迫使每个神经元都必须“自力更生”，学习到更独立、更鲁棒的特征，而不是过度依赖少数几个邻居。
2. 模型集成 (Ensemble) 的思想: 每次应用 Dropout，我们都相当于在训练一个结构不同的“子网络”。整个训练过程，就像是同时训练了成千上万个共享权重的子网络。在最后做预测时，我们保留所有神经元，这近似于将所有这些子网络的预测结果进行平均。模型集成是公认的提升性能、防止过拟合的强大技术。
实践建议:
- Dropout Rate p 是需要设置的超参数，常见范围是 0.2 到 0.5。
- 通常用在网络中容易过拟合的全连接层，对于卷积层，由于其参数共享的特性，过拟合风险较低，可以不用或使用较小的 Dropout Rate。
- 极其重要的一点: Dropout 只在训练 (train) 模式下开启。在评估或预测 (eval / inference) 模式下，必须关闭 Dropout，并使用完整的网络进行计算。幸运的是，所有主流框架都会自动帮你处理这个模式切换。

3. Early Stopping (早停)

我们在上一节已经提过，但从本质上讲，早停也是一种非常有效且简单的正则化方法。它的逻辑是：在模型开始过拟合之前就停止训练。通过监控验证集的性能，我们捕捉到泛化能力达到顶峰的时刻，从而避免了模型在训练集上继续“画蛇添足”。

4. Data Augmentation (数据增强)

“给我更多的数据！”——这是对抗过拟合最根本、最有效的方法。但获取新数据成本高昂。数据增强则提供了一种“无中生有”的廉价替代方案。

工作原理:
通过对现有的训练数据进行一系列随机变换，来创造出新的、合理的训练样本。
- 图像领域: 随机旋转、裁剪、翻转、缩放、调整亮度和对比度等。
- 文本领域: 同义词替换、随机插入/删除词语、回译（如：中文->英文->中文）等（学术裁缝降低查重doge）。
为什么有效？
数据增强极大地扩充了训练集的多样性。它教会模型什么是“不变性” (Invariance)。例如，一张猫的图片，无论向左旋转 15 度，还是亮度稍暗一点，它依然是一只猫。通过学习这些增强样本，模型被迫关注物体本身的核心特征，而不是图片的方向、光照等次要信息，从而大大提升了泛化能力。

数据增强绝非“万金油”，这种方案往往要求对模型应用的邻域有一定的了解，盲目使用或错误使用确实会适得其反。

几个典型的反面案例：

数字识别 (MNIST)：对数字“6”进行垂直翻转，它就变成了“9”。这种增强方式完全改变了样本的标签和语义，会严重误导模型。
医学影像（如X光片）：在医学图像中，方向和位置通常包含着至关重要的诊断信息。对一张胸部X光片进行随意的水平翻转，可能会将左肺和右肺的位置颠倒，这是绝对不能接受的。
交通标志识别：对一个“停止”标志进行颜色抖动，如果将其主色调从红色变成了绿色，模型可能会错误地将其与“通行”标志关联起来。

三、其他关键超参数

除了上述参数，还有一些选择虽然不常在“调参”的语境下被反复调整，但它们是构建和训练模型的基础性决策，选错了同样会导致灾难性后果。

1. 网络架构 (Network Architecture)

这其实是“最大”的一组超参数，它定义了模型的骨架。

深度 (Depth): 网络包含多少层？更深的网络能学习到更复杂、更抽象的层次化特征，但也更容易出现梯度消失/爆炸和过拟合。
宽度 (Width): 每层包含多少个神经元/通道？更宽的网络能在同一层级学习到更丰富的特征。
实践建议: 对于初学者，尽量避免从零开始发明一个全新的架构。最佳实践是站在巨人的肩膀上，首先选择一个在你的任务领域被验证过的经典架构（如图像领域的 ResNet、VGG，NLP 领域的 BERT、GPT），然后在此基础上进行微调 (Fine-tuning)。

2. 激活函数 (Activation Function)

激活函数的作用是为神经网络引入非线性。没有它，无论你的网络有多少层，本质上都只是一个简单的线性模型，无法学习复杂的数据模式。

旧时代的 Sigmoid / Tanh: 它们的主要问题在于容易导致梯度消失，使得深层网络的训练非常困难，现在已基本被淘汰。

Sigmoid：

$f(x) = \frac{1}{1 + e^{-x}}$

Tanh (Hyperbolic Tangent)

$f(x) = \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$

现代的王者 ReLU (Rectified Linear Unit): f(x) = max(0, x)。它形式简单、计算高效，并且在正数区间不会饱和，极大地缓解了梯度消失问题。是当今最常用、最默认的选择。它的一个缺点是“Dying ReLU”问题（负数区间的神经元可能永远无法被激活）。

$f(x) = \begin{cases} x & \text{if } x > 0 \\ 0 & \text{if } x \le 0 \end{cases}$

ReLU 的变体 (Leaky ReLU, GELU等): 为了解决 Dying ReLU 问题，出现了 Leaky ReLU（允许负数区间有微小的梯度）。而 GELU 则是一种更平滑的变体，在 Transformer 模型中被广泛使用。
实践建议: 默认使用 ReLU。如果发现训练中有很多神经元“死亡”，可以换成 Leaky ReLU。如果你在用 Transformer，那就用 GELU。

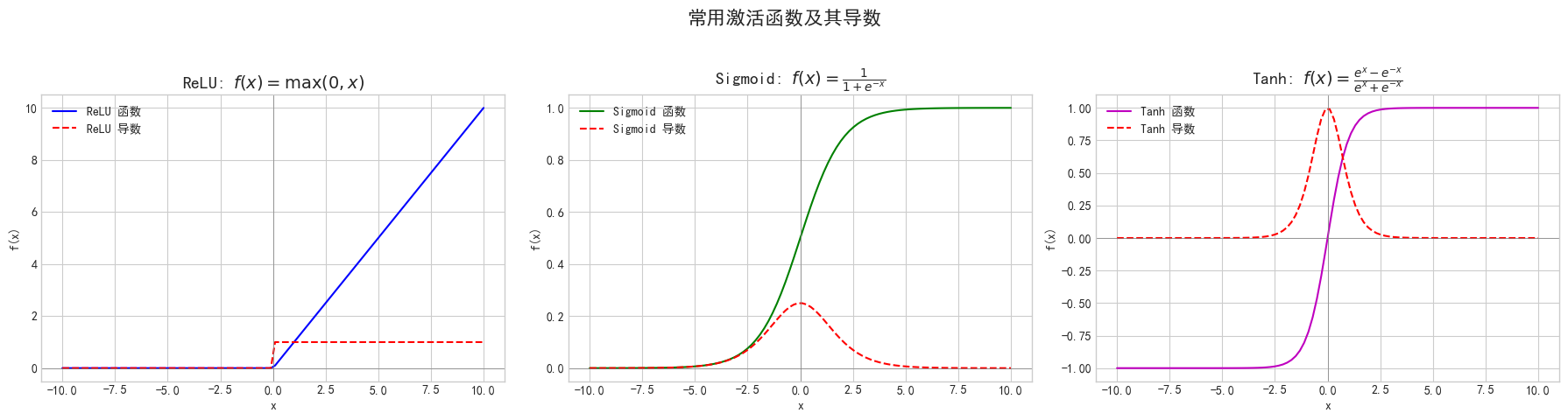
(图片使用numpy和matplotlib绘制得到）

3. 权重初始化 (Weight Initialization)

在训练开始前，模型的权重需要被赋予一个初始值。这个看似简单的步骤却至关重要。

问题: 如果初始权重过大，可能导致梯度爆炸；如果过小，则可能导致梯度消失，使得网络无法有效学习。
解决方案: 现代深度学习框架已经内置了成熟的初始化策略。最著名的是：
- Xavier / Glorot 初始化: 适用于 Sigmoid / Tanh 激活函数。
- He 初始化: 专门为 ReLU 及其变体设计，是目前的主流。
实践建议: 大多数情况下，你不需要手动设置这个。主流框架（PyTorch, TensorFlow）在创建层时会自动选择合适的默认初始化方法（通常是 He 初始化）。只需要知道它的存在和重要性即可。

四、总结

经过上下两篇的系统梳理，我们一同探索了深度学习模型训练中那些至关重要的超参数。现在，让我们对这次旅程的核心知识点进行一次全面且理性的回顾。

回顾上篇：构建高效的训练引擎

上一篇博客中，我们聚焦于模型训练的两个“发动机”级别的超参数，它们共同决定了模型参数更新的效率与方向。

学习率 (Learning Rate)：作为模型更新的步长，其设定直接关系到训练的稳定性和收敛速度。我们探讨了从固定学习率到使用 Warm-up 和 学习率调度器 (Scheduler) 进行动态调整的必要性，以平衡初期的快速探索和后期的精细微调。
优化器 (Optimizer)：作为参数更新的具体算法，我们从最基础的 SGD 出发，了解了 Momentum 如何帮助克服局部最优和鞍点，并深入分析了以 Adam 为代表的自适应优化器家族如何为每个参数提供个性化的学习率，从而实现更快速、更稳健的收敛。

核心结论是，一个精心设计的动态学习率策略与一个强大的自适应优化器（如Adam/AdamW）相结合，是保障模型训练成功的基础。

本篇核心：精细化训练与模型的泛化之道

在本篇中，我们将视野从“如何更新参数”扩展到“如何组织训练”以及“如何防止模型学偏”。

训练结构 (Batch Size & Epochs)：我们明确了 Batch Size 在训练速度、内存消耗和模型泛化能力之间的权衡关系。较大的 Batch Size 可以加速训练并稳定梯度，但可能陷入更尖锐的最小值；较小的 Batch Size 则引入了噪声，有助于模型跳出局部最优，提升泛化能力。而 Epochs 的数量则需要通过监控验证集性能来确定，早停 (Early Stopping) 是防止训练过度、找到最佳“火候”的关键实践。
正则化策略 (Regularization)：这是对抗过拟合的“军火库”。我们系统地学习了：
- L1 & L2 正则化：通过在损失函数中增加权重惩罚项，限制模型复杂度。
- Dropout：在训练中随机“失活”神经元，强制网络学习更鲁棒的特征。
- 数据增强 (Data Augmentation)：通过变换现有数据来扩充训练集，是提升模型泛化能力最根本有效的方法之一。
基础性决策：最后，我们也强调了如网络架构、激活函数和权重初始化等 foundational choices 的重要性。它们共同构成了模型的“骨架”与“血肉”，是后续所有优化的基石。