基于图像的三维重建——捆绑调整(6)

---

前言

Bundle Adjustment译为光束法平差或者束调整、捆绑调整。BA问题主要是对三维点位置和相机参数进行非线性优化，而我们可以把BA问题看成最小化重投影误差问题，同时这也是一个非线性最小二乘问题。

---

基础知识

重投影

由前面可知，我们可以通过特征点检测与匹配，得到多对特征匹配点，使用对极几何可以求得相机的位姿。由下面公式可得，我们可以通过空间点P的坐标求得空间点P投影在图像中的像素坐标，但是这个像素点坐标是先通过位姿估计，再通过公式计算出来的，相当于这个像素坐标是估算出来的。这个过程称为重投影。

重投影误差

如果完全没有误差，那么两者的坐标是一样的，但这是不可能的，不管是实际测量出来的像素坐标还是通过位姿估算+重投影计算出来的像素坐标，都是有误差的，将实际值和估算值一减，就得到了重投影误差。

最小化重投影误差

由于两张图片中有很多特征匹配点，将所有特征点重投影误差求和，取平方，再乘以1/2，这就构建了一个非线性最小二乘问题了，将里面的位姿、空间点作为优化的对象，最小化重投影误差，即得到一个优化后的结果，这就是所谓的BA。

无约束非线性最小优化问题

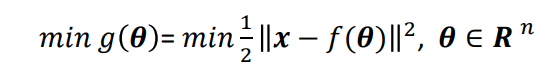
上述问题的最优解通常是指它的局部最优解，对初始值较为敏感，因此需要一个较好的初始值。

求解方法

BA问题被归结为一个非常大的非线性最小二乘问题，通常用Levenberg-Marquardt(LM)算法求解，但在介绍LM算法之前，分别介绍一下最速下降法和牛顿法。

最速下降法

算法介绍

在解决无约束问题时，经常用到的一类算法是最速下降法。
假设g($\theta$)在$\theta$_t处可微，则它在$\theta$_t处有Taylor展开式为（略去高阶不计）：

其中$\theta$=$\theta$_t+$\delta \theta$
可以看到，当（$\nabla$g($\theta$_t))^T$\delta \theta$<0时可保证g($\theta$)的值是在下降。
由$\Delta$g=g($\theta$)-$\theta$_t=($\nabla$g($\theta$_t))^T$\delta \theta$可见，函数变化量$\Delta$g为向量$\nabla$g($\theta$_t)与$\delta \theta$的内积，根据向量内积的计算公式，得$\Delta$g=||$\nabla$g($\theta$_t)|| ||$\delta \theta$|| cos$\alpha$,因为cos$\alpha$$\in$[-1,1],当且仅当$\delta \theta$的方向取梯度反方向时，函数值下降最快。当然这只是一个方向，通常我们还需要指定一个步长$\lambda$

算法流程

1）给定初始点$\theta$₀,终止控制函数$ϵ$>0和步长$\lambda$，令t=0;
2)计算$\nabla$g($\theta$_t)，若||$\nabla$g($\theta$_t)||$\le$$ϵ$,停止迭代，输出$\theta$_t,否则进行下一步；
3）取$\theta$_t+1=$\theta$_t –$\lambda$$\nabla$g($\theta$_t),t=t+1,转2)步。

牛顿法

算法介绍

对于非线性优化问题，牛顿法提供了一种求解办法:假设任务是优化一个目标函数f，求函数f的极值，可以转化为求解函数f的导数f’=0的问题。
假设g($\theta$)在$\theta$_t处二阶可微，且假定二阶导数$\nabla$²g($\theta$)总是正定的，则它在$\theta$_t处以g($\theta$)的二阶近似函数Q($\theta$)的极小值点作为下一次迭代点$\theta$_t+1。

上式对$\delta \theta$求梯度并令其等于0，可以得到：

算法流程

1）给定初始点$\theta$₀,终止控制函数$ϵ$>0和步长$\lambda$，令t=0;
2)计算$\nabla$g($\theta$_t)，若||$\nabla$g($\theta$_t)||$\le$$ϵ$,停止迭代，输出$\theta$_t,否则进行下一步；
3）取$\theta$_t+1=$\theta$_t -($\nabla$²g($\theta$_t))^-1$\nabla$g($\theta$_t),t=t+1,转2)步。

Levenberg-Marquardt法

算法介绍

它的原理是一种“信赖阈”的方法，当收敛速度较快时，增大信赖域，使算法趋向于牛顿法；当收敛速度较慢时，减小信赖域，使算法趋向于最速下降法。

为实现

可得$\nabla$g($\theta$_t)=-J^T($\theta$_t)(x - f($\theta$_t)),其中J($\theta$_t)=$\nabla$f($\theta$_t)。

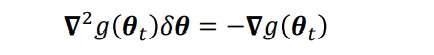
将上述公式中的$\nabla$²g($\theta$_t)替换成J^T($\theta$_t)J($\theta$_t) + $\frac{1}{\lambda }$I（$\lambda$为信赖域半径），可得增量正规方程

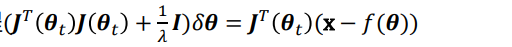
当$\lambda$趋向于无穷大时，J^T($\theta$_t)J($\theta$_t)$\delta \theta$=-$\nabla$g($\theta$_t)
当$\lambda$趋向于零时，$\delta \theta$= -$\nabla$g($\theta$_t)

算法流程

1）t=0时，选取初始点$\theta$₀,终止控制函数$ϵ$，令e⁰=||x-f($\theta$₀)||²,$\lambda$=10^-3;
2)计算J^T($\theta$_t)
3）构造增量正规方程(J^T($\theta$_t)J($\theta$_t) + $\frac{1}{\lambda }$I)$\delta \theta$=J^T($\theta$_t)(x - f($\theta$))
4)通过求解增量正规方程，得到$\delta \theta$。
如果||x - f($\theta$+$\delta \theta$)||<e^k,令$\theta$_t+1=$\theta$_t+$\delta$($\theta$）,
  如果||$\delta$($\theta$)||<$ϵ$,终止迭代；
  否则令$\lambda$_t+1=10$\lambda$_t,t=t+1,执行第2）步
否则||x - f($\theta$+$\delta \theta$)||≥e^k，令$\lambda$_t+1=0.1$\lambda$_t，执行第3）步

增量规方程的求解

BAJacobian矩阵推导免费下载。