泰勒公式
泰勒公式(Taylor’s Formula)是一个用函数在某点的信息描述其附近取值的公式。其初衷是用多项式来近似表示函数在某点周围的情况。
对于一般的函数,泰勒公式的系数的选择依赖于函数在一点的各阶导数值。函数f(x)在 x 0 x_0 x0处的基本形式如下:
f ( x ) = ∑ n = 0 ∞ f ( n ) ( x 0 ) n ! ( x − x 0 ) n = f ( x 0 ) + f ( 1 ) ( x 0 ) ( x − x 0 ) + f ( 2 ) ( x 0 ) 2 ( x − x 0 ) 2 + ⋯ + f ( n ) ( x 0 ) n ! ( x − x 0 ) n \begin{aligned} f(x) & =\sum_{n=0}^{\infty} \frac{f^{(n)}\left(x_0\right)}{n !}\left(x-x_0\right)^n \\ & =f\left(x_0\right)+f^{(1)}\left(x_0\right)\left(x-x_0\right)+\frac{f^{(2)}\left(x_0\right)}{2}\left(x-x_0\right)^2+\cdots+\frac{f^{(n)}\left(x_0\right)}{n !}\left(x-x_0\right)^n\end{aligned} f(x)=n=0∑∞n!f(n)(x0)(x−x0)n=f(x0)+f(1)(x0)(x−x0)+2f(2)(x0)(x−x0)2+⋯+n!f(n)(x0)(x−x0)n
还有另外一种常见的写法,
x
t
+
1
=
x
t
+
Δ
x
x^{t+1}=x^t+\Delta x
xt+1=xt+Δx ,将
f
(
x
t
+
1
)
f\left(x^{t+1}\right)
f(xt+1) 在
x
t
x^t
xt 处进行泰勒展开,得:
f
(
x
t
+
1
)
=
f
(
x
t
)
+
f
1
(
x
t
)
Δ
x
+
f
2
(
x
t
)
2
Δ
x
2
+
⋯
f\left(x^{t+1}\right)=f\left(x^t\right)+f^1\left(x^t\right) \Delta x+\frac{f^2\left(x^t\right)}{2} \Delta x^2+\cdots
f(xt+1)=f(xt)+f1(xt)Δx+2f2(xt)Δx2+⋯
补充:
1.多项式的函数图像特点
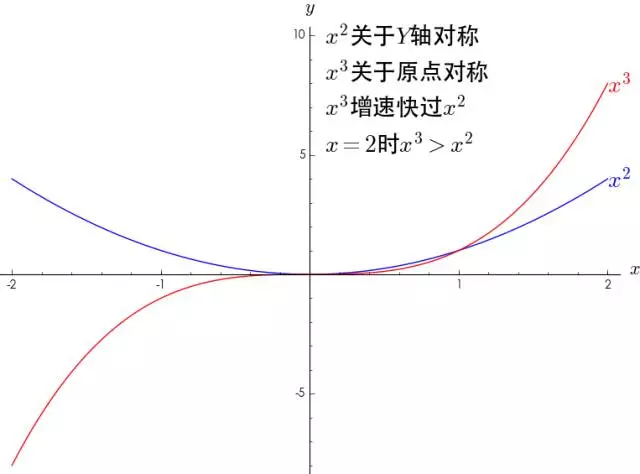
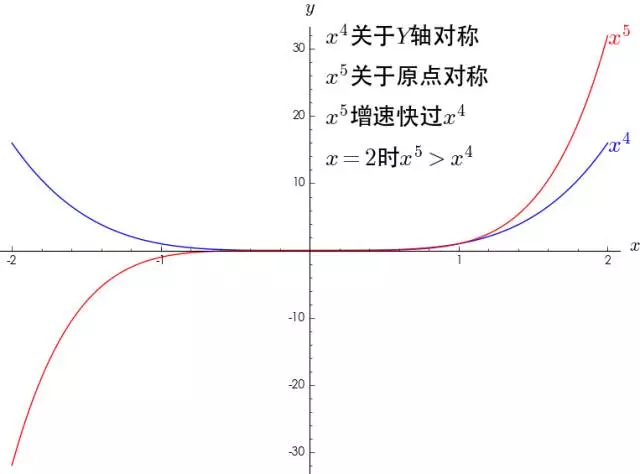
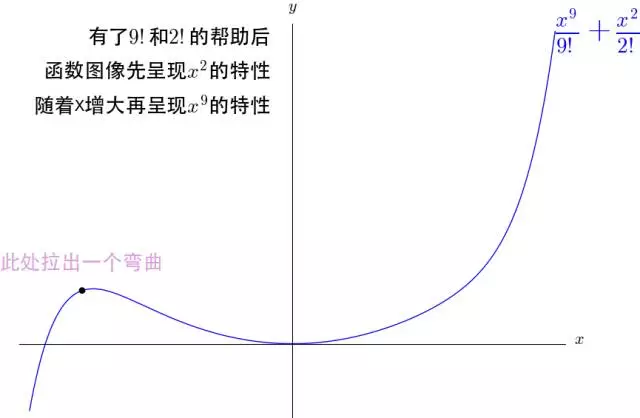
∑ n = 0 N f ( n ) ( 0 ) n ! x n \sum_{n=0}^N \frac{f^{(n)}(0)}{n !} x^n ∑n=0Nn!f(n)(0)xn 展开来就是 f ( 0 ) + f ′ ( 0 ) x + f ′ ′ ( 0 ) 2 ! x 2 + ⋯ + f ( N ) ( 0 ) N ! x N f(0)+f^{\prime}(0) x+\frac{f^{\prime \prime}(0)}{2 !} x^2+\cdots+\frac{f^{(N)}(0)}{N !} x^N f(0)+f′(0)x+2!f′′(0)x2+⋯+N!f(N)(0)xN,我们单独分析 x 2 , x 3 等幂函数 x^2,x^3等幂函数 x2,x3等幂函数
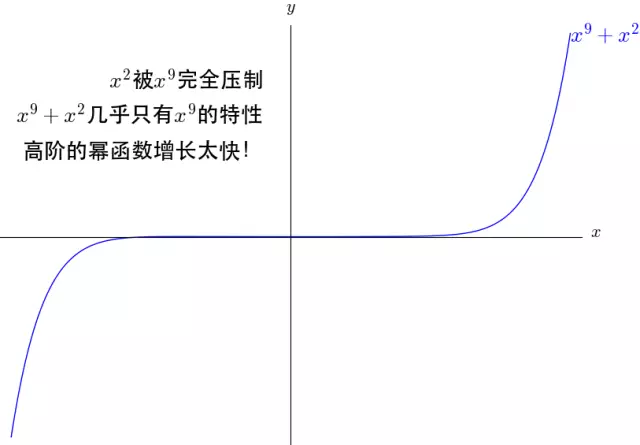
注意:先呈现 x 9 x^9 x9的特性,再呈现 x 2 x^2 x2的特性,最后呈现 x 9 x^9 x9的特性
结论:
- 可以看到,幂函数其实只有两种形态:一种是关于Y轴对称,一种是关于原点对称并且指数越大,增长速度越大;
- x 2 完全被 x 9 压制,图像上只有 x 9 的图像特点 x^2完全被x^9压制,图像上只有x^9的图像特点 x2完全被x9压制,图像上只有x9的图像特点,有了9!和2!的帮助后,图像先呈现 x 9 x^9 x9的特性,再呈现 x 2 x^2 x2的特性,最后呈现 x 9 x^9 x9的特性
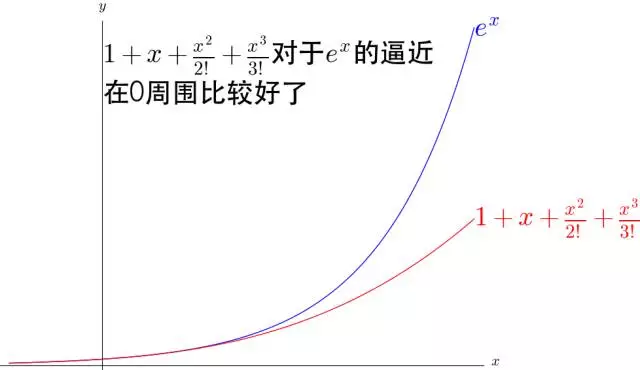
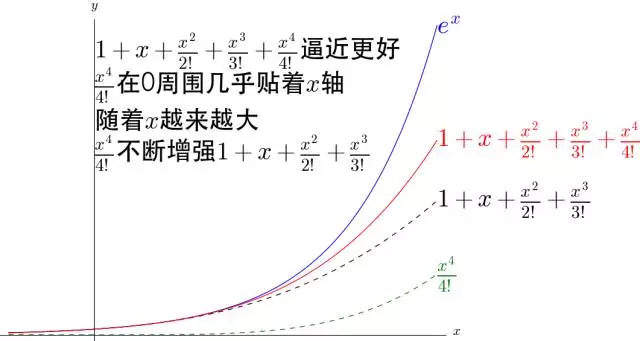
2.例子:用多项式对 e x e^x ex 进行逼近
e x = 1 + x + 1 2 ! x 2 + ⋯ + 1 n ! x n + R n ( x ) e^x=1+x+\frac{1}{2 !} x^2+\cdots+\frac{1}{n !} x^n+R_n(x) ex=1+x+2!1x2+⋯+n!1xn+Rn(x)
可以看出, 1 n ! x n \frac{1}{n !} x^n n!1xn 不断的弯曲着那根多项式形成的铁丝去逼近 e x e^x ex 。并且 n n n 越大,贴合 e x e^x ex的区域就越大。
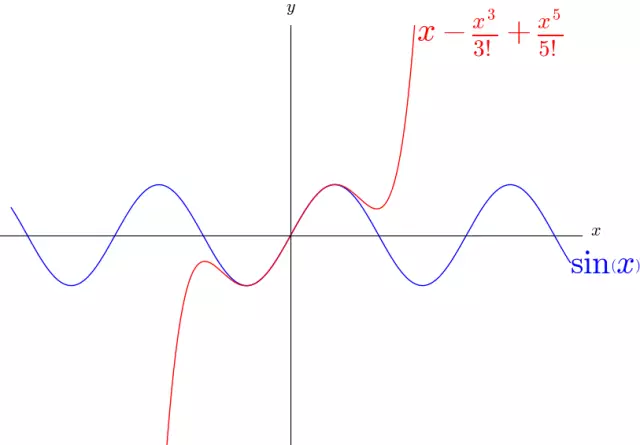
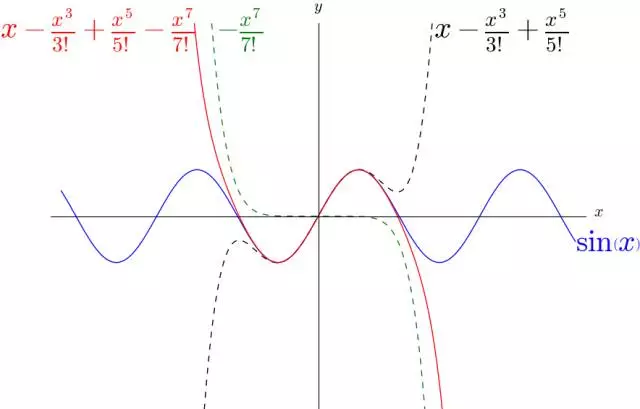
3.用多项式对sin(x) 进行逼近
sin ( x ) \sin (x) sin(x) 是周期函数 Q Q Q ,有非常多的弯曲,难以想象可以用多项式进行逼近。
sin ( x ) = x − 1 3 ! x 3 + ⋯ + ( − 1 ) n ( 2 n + 1 ) ! x ( 2 n + 1 ) + R n ( x ) 。 \sin (x)=x-\frac{1}{3 !} x^3+\cdots+\frac{(-1)^n}{(2 n+1) !} x^{(2 n+1)}+R_n(x) \text { 。 } sin(x)=x−3!1x3+⋯+(2n+1)!(−1)nx(2n+1)+Rn(x) 。
可以看到 1 7 ! x 7 \frac{1}{7 !} x^7 7!1x7 在适当的位置,改变了 x − 1 3 ! x 3 + 1 5 ! x 5 x-\frac{1}{3 !} x^3+\frac{1}{5 !} x^5 x−3!1x3+5!1x5 的弯曲方向,最终让 x − 1 3 ! x 3 + 1 5 ! x 5 − 1 7 ! x 7 x-\frac{1}{3 !} x^3+\frac{1}{5 !} x^5-\frac{1}{7 !} x^7 x−3!1x3+5!1x5−7!1x7 更好的逼近了 sin ( x ) \sin (x) sin(x) 。
4.泰勒公式与拉格朗日中值定理的关系
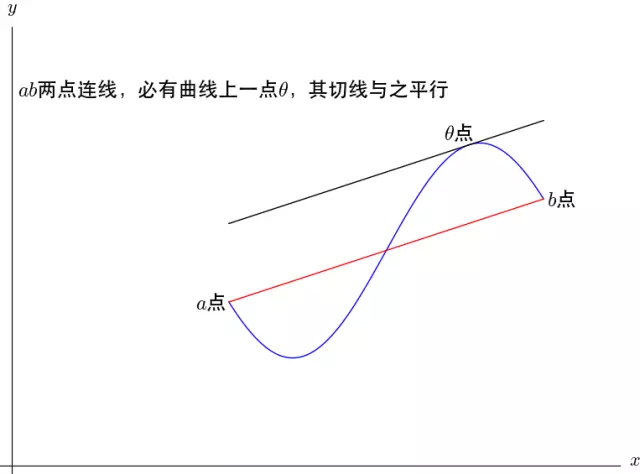
拉格朗日中值定理:如果函数 f ( x ) f(x) f(x) 满足,在 [ a , b ] [a, b] [a,b] 上连续,在 ( a , b ) (a, b) (a,b) 上可导,那么至少有一点 θ ( a < θ < b ) \theta(a<\theta<b) θ(a<θ<b) )使等式 f ′ ( θ ) = f ( a ) − f ( b ) a − b f^{\prime}(\theta)=\frac{f(a)-f(b)}{a-b} f′(θ)=a−bf(a)−f(b) 成立。
这个和泰勒公式有什么关系?
泰勒公式有个余项 R n ( x ) R_n(x) Rn(x) 我们一直没有提。余项即使用泰勒公式估算的误差,即 f ( x ) − ∑ n = 0 N f ( n ) ( a ) n ! ( x − a ) n = R n ( x ) f(x)-\sum_{n=0}^N \frac{f^{(n)}(a)}{n !}(x-a)^n=R_n(x) f(x)−∑n=0Nn!f(n)(a)(x−a)n=Rn(x)
余项的代数式是, R n ( x ) = f ( n + 1 ) ( θ ) ( n + 1 ) ! ( x − a ) ( n + 1 ) R_n(x)=\frac{f^{(n+1)}(\theta)}{(n+1) !}(x-a)^{(n+1)} Rn(x)=(n+1)!f(n+1)(θ)(x−a)(n+1) ,其中 a < θ < x a<\theta<x a<θ<x ,这里我么假定函数 f ( x ) f(x) f(x)在含a的某个开区间内有连续的n+1阶导数。当 N = 0 N=0 N=0 的时候,根据泰勒公式有, f ( x ) = f ( a ) + f ′ ( θ ) ( x − a ) f(x)=f(a)+f^{\prime}(\theta)(x-a) f(x)=f(a)+f′(θ)(x−a) ,把拉格朗日中值定理中的 b b b 换成 x x x ,那么拉格朗日中值定理根本就是 N = 0 N=0 N=0 时的泰勒公式。
5.泰勒公式是怎么推导的?
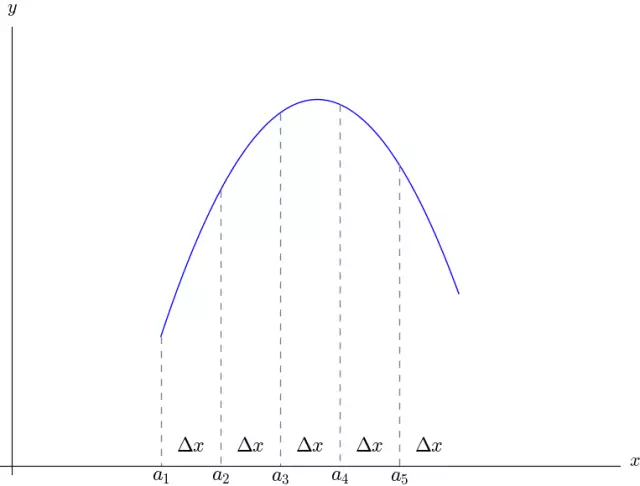
以直代曲、化整为零
如上图,把曲线等分为 n n n 份,分别为 a 1 , a 2 , ⋯ , a n a_1 , a_2 , \cdots , a_n a1,a2,⋯,an ,令 a 1 = a , a 2 = a + Δ x a_1=a , a_2=a+\Delta x a1=a,a2=a+Δx , ⋯ , a n = a + ( n − 1 ) Δ x \cdots , a_n=a+(n-1) \Delta x ⋯,an=a+(n−1)Δx 。我们可以推出 ( Δ 2 , Δ 3 \left(\Delta^2 , \Delta^3\right. (Δ2,Δ3 可以认为是二阶、三阶微分,其准确的数学用语是差分,和微分相比,一个是有限量,一个是极限量)。
补充:牛顿插值
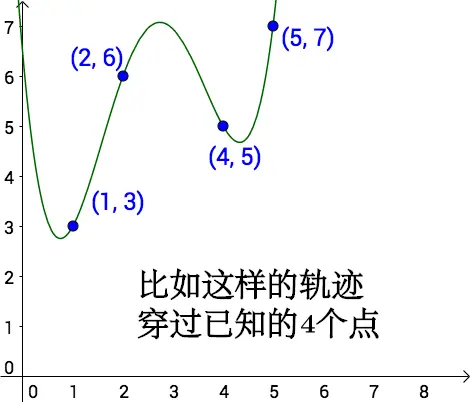
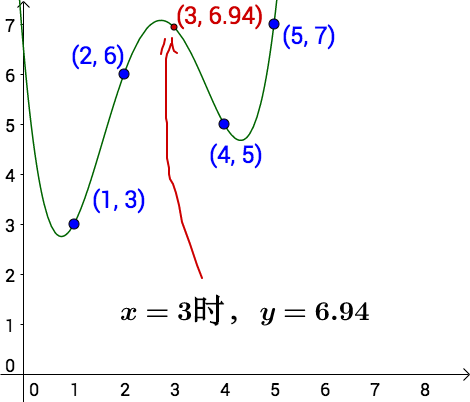
引入:对于已知的4组数据【(1, 3), (2, 6), (4, 5), (5, 7)】,如何预测未知数据(3, ?)
插值
所以根据这4个点,我们随便猜测一个运动轨迹:
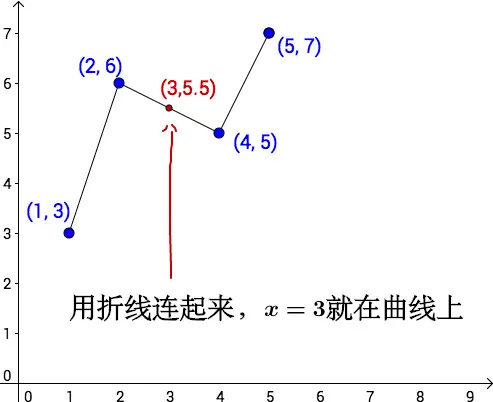
线性插值
线性插值法中根本不需要x=1,x=5的数据,只需要x=2, x=4
多项式插值
线性方程
联立方程组求出 f ( x ) = a + b x + c x 2 + d x 3 f(x)=a+b x+c x^2+d x^3 f(x)=a+bx+cx2+dx3的四个多项式系数a,b,c,d
{ 3 = a + b + c + d 6 = a + 2 b + 4 c + 8 d 5 = a + 4 b + 16 c + 64 d 7 = a + 5 b + 25 c + 125 d \left\{\begin{array}{l}3=a+b+c+d \\ 6=a+2 b+4 c+8 d \\ 5=a+4 b+16 c+64 d \\ 7=a+5 b+25 c+125 d\end{array}\right. ⎩ ⎨ ⎧3=a+b+c+d6=a+2b+4c+8d5=a+4b+16c+64d7=a+5b+25c+125d
缺点:
- 计算量大,若数据量,会给计算带来较大阻碍
- 增加一个观测数据,整个计算过程就要重新来
于是就产生了牛顿插值法
牛顿插值法
每增加一个点,不会导致之前的重新计算,只需要算和新增点有关的就可以了
观察 b 1 , b 2 b_1, b_2 b1,b2 的特点,不断重复上述过程,就可以得到牛顿插值法。
求解流程
先从求满足两个点 ( x 0 , f ( x 0 ) ) , ( x 1 , f ( x 1 ) ) \left(x_0, f\left(x_0\right)\right),\left(x_1, f\left(x_1\right)\right) (x0,f(x0)),(x1,f(x1)) 的函数 f 1 ( x ) f_1(x) f1(x) 说起:
假设 f 1 ( x ) = f ( x 0 ) + b 1 ( x − x 0 ) f_1(x)=f\left(x_0\right)+b_1\left(x-x_0\right) f1(x)=f(x0)+b1(x−x0) ,
令 f 1 ( x 1 ) = f ( x 1 ) : \text { 令 } f_1\left(x_1\right)=f\left(x_1\right) \text { : } 令 f1(x1)=f(x1) :⟹ b 1 = f ( x 1 ) − f ( x 0 ) x 1 − x 0 ⟹ f 1 ( x ) = f ( x 0 ) + f ( x 1 ) − f ( x 0 ) x 1 − x 0 ( x − x 0 ) \begin{aligned} & \Longrightarrow b_1=\frac{f\left(x_1\right)-f\left(x_0\right)}{x_1-x_0} \\ & \Longrightarrow f_1(x)=f\left(x_0\right)+\frac{f\left(x_1\right)-f\left(x_0\right)}{x_1-x_0}\left(x-x_0\right) \end{aligned} ⟹b1=x1−x0f(x1)−f(x0)⟹f1(x)=f(x0)+x1−x0f(x1)−f(x0)(x−x0)
现在我们增加一个点, ( x 0 , f ( x 0 ) ) , ( x 1 , f ( x 1 ) ) , ( x 2 , f ( x 2 ) ) \left(x_0, f\left(x_0\right)\right),\left(x_1, f\left(x_1\right)\right),\left(x_2, f\left(x_2\right)\right) (x0,f(x0)),(x1,f(x1)),(x2,f(x2)) ,求满足这三个点的函数 f 2 ( x ) f_2(x) f2(x)
假设 f 2 ( x ) = f 1 ( x ) + b 2 ( x − x 0 ) ( x − x 1 ) f_2(x)=f_1(x)+b_2\left(x-x_0\right)\left(x-x_1\right) f2(x)=f1(x)+b2(x−x0)(x−x1) ,
令 f 2 ( x 2 ) = f ( x 2 ) f_2\left(x_2\right)=f\left(x_2\right) f2(x2)=f(x2)
⟹ b 2 = [ f ( x 2 ) − f ( x 1 ) x 2 − x 1 ] − [ f ( x 1 ) − f ( x 0 ) x 1 − x 0 ] x 2 − x 0 ⟹ f 2 ( x ) = f ( x 0 ) + f ( x 1 ) − f ( x 0 ) x 1 − x 0 ( x − x 0 ) + [ f ( x 2 ) − f ( x 1 ) x 2 − x 1 ] − [ f ( x 1 ) − f ( x 0 ) x 1 − x 0 ] x 2 − x 0 ( x − x 0 ) ( x − x 1 ) \begin{array}{ll} \Longrightarrow b_2=\ & \frac{\left[\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}\right]-\left[\frac{f\left(x_1\right)-f\left(x_0\right)}{x_1-x_0}\right]}{x_2-x_0} \\ \Longrightarrow f_2(x)=\quad & f\left(x_0\right)+\frac{f\left(x_1\right)-f\left(x_0\right)}{x_1-x_0}\left(x-x_0\right) \\ & +\frac{\left[\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}\right]-\left[\frac{f\left(x_1\right)-f\left(x_0\right)}{x_1-x_0}\right]}{x_2-x_0}\left(x-x_0\right)\left(x-x_1\right) \end{array} ⟹b2= ⟹f2(x)=x2−x0[x2−x1f(x2)−f(x1)]−[x1−x0f(x1)−f(x0)]f(x0)+x1−x0f(x1)−f(x0)(x−x0)+x2−x0[x2−x1f(x2)−f(x1)]−[x1−x0f(x1)−f(x0)](x−x0)(x−x1)
b 1 , b 2 b_1, b_2 b1,b2 看起来蛮有特点的,我们把特点提炼一下。
一阶均差:
f [ x i , x j ] = f ( x i ) − f ( x j ) x i − x j , i ≠ j f\left[x_i, x_j\right]=\frac{f\left(x_i\right)-f\left(x_j\right)}{x_i-x_j}, i \neq j f[xi,xj]=xi−xjf(xi)−f(xj),i=j二阶均差 是一阶均差的均差:
f [ x i , x j , x k ] = f [ i , j ] − f [ j , k ] x i − x k , i ≠ j ≠ k f\left[x_i, x_j, x_k\right]=\frac{f[i, j]-f[j, k]}{x_i-x_k}, i \neq j \neq k f[xi,xj,xk]=xi−xkf[i,j]−f[j,k],i=j=k
三阶均差 就是二阶均差的均差,以此类推,我们得到 ( x 0 , f ( x 0 ) ) , ( x 1 , f ( x 1 ) ) , ( x 2 , f ( x 2 ) ) . . . ( x n , f ( x n ) ) \left(x_0, f\left(x_0\right)\right),\left(x_1, f\left(x_1\right)\right),\left(x_2, f\left(x_2\right)\right)...(x_n,f(x_n)) (x0,f(x0)),(x1,f(x1)),(x2,f(x2))...(xn,f(xn)) 牛顿插值法为:
f ( x ) = f ( x 0 ) + f [ x 0 , x 1 ] ( x − x 0 ) + f [ x 0 , x 1 , x 2 ] ( x − x 0 ) ( x − x 1 ) + ⋯ + f [ x 0 , x 1 , ⋯ , x n − 2 , x n − 1 ] ( x − x 0 ) ( x − x 1 ) ⋯ ( x − x n − 2 ) + f [ x 0 , x 1 , ⋯ , x n − 1 , x n ] ( x − x 0 ) ( x − x 1 ) ⋯ ( x − x n − 1 ) \begin{aligned} f(x)= & f\left(x_0\right)+f\left[x_0, x_1\right]\left(x-x_0\right) \\ & +f\left[x_0, x_1, x_2\right]\left(x-x_0\right)\left(x-x_1\right)+\cdots \\ & +f\left[x_0, x_1, \cdots, x_{n-2}, x_{n-1}\right]\left(x-x_0\right)\left(x-x_1\right) \cdots\left(x-x_{n-2}\right) \\ & +f\left[x_0, x_1, \cdots, x_{n-1}, x_n\right]\left(x-x_0\right)\left(x-x_1\right) \cdots\left(x-x_{n-1}\right) \end{aligned} f(x)=f(x0)+f[x0,x1](x−x0)+f[x0,x1,x2](x−x0)(x−x1)+⋯+f[x0,x1,⋯,xn−2,xn−1](x−x0)(x−x1)⋯(x−xn−2)+f[x0,x1,⋯,xn−1,xn](x−x0)(x−x1)⋯(x−xn−1)注释:
单独看等号右边第一项 f ( x ) = f ( x 0 ) f(x)=f(x_0) f(x)=f(x0)是把 ( x 0 , f ( x 0 ) ) (x_0, f(x_0)) (x0,f(x0))带入的式子;右边第二项 f ( x ) = f [ x 0 , x 1 ] ( x − x 0 ) f(x)=f\left[x_0, x_1\right]\left(x-x_0\right) f(x)=f[x0,x1](x−x0)是把 ( x 1 , f ( x 1 ) ) (x_1, f(x_1)) (x1,f(x1))带入的式子,并保证 x = x 0 x=x_0 x=x0时, f ( x ) = 0 f(x)=0 f(x)=0;右边第三项 f ( x ) = f [ x 0 , x 1 , x 2 ] ( x − x 0 ) ( x − x 1 ) f(x)=f\left[x_0, x_1, x_2\right]\left(x-x_0\right)\left(x-x_1\right) f(x)=f[x0,x1,x2](x−x0)(x−x1)是把 ( x 2 , f ( x 2 ) ) (x_2, f(x_2)) (x2,f(x2))带入的式子,并保证 x = x 0 或者 x = x 1 x=x_0或者x=x_1 x=x0或者x=x1时, f ( x ) = 0 f(x)=0 f(x)=0。从而保证新增一个点,只需要计算相关的差分就可以了
5.泰勒公式是怎么推导的?
泰勒把牛顿插值法做了一些改造。
首先,设 f ( x ) f(x) f(x) 是一个函数,它在 x 0 , x 0 + Δ x , x 0 + 2 Δ x , x 0 + 3 Δ x , ⋯ , x 0 + n Δ x x_0, x_0+\Delta x, x_0+2 \Delta x, x_0+3 \Delta x, \cdots, x_0+n \Delta x x0,x0+Δx,x0+2Δx,x0+3Δx,⋯,x0+nΔx 的值已知(和之前的相比,相当于每个点都是等距离间隔的,间隔 Δ x \Delta x Δx ),令:
Δ f ( x 0 ) = f ( x 0 + Δ x ) − f ( x 0 ) , 也称为一阶差分 , Δ f ( x 0 + Δ x ) = f ( ( x 0 + Δ x ) + Δ x ) − f ( x 0 + Δ x ) , Δ f ( x 0 + 2 Δ x ) = f ( x 0 + 3 Δ x ) − f ( x 0 + 2 Δ x ) \begin{aligned} & \Delta f\left(x_0\right)=f\left(x_0+\Delta x\right)-f\left(x_0\right) , \text { 也称为一阶差分 } , \\ & \Delta f\left(x_0+\Delta x\right)=f\left((x_0+ \Delta x )+ \Delta x\right)-f\left(x_0+\Delta x\right) , \\ & \Delta f\left(x_0+2 \Delta x\right)=f\left(x_0+3 \Delta x\right)-f\left(x_0+2 \Delta x\right) \end{aligned} Δf(x0)=f(x0+Δx)−f(x0), 也称为一阶差分 ,Δf(x0+Δx)=f((x0+Δx)+Δx)−f(x0+Δx),Δf(x0+2Δx)=f(x0+3Δx)−f(x0+2Δx)进一步令:
Δ 2 f ( x 0 ) = Δ f ( x 0 + Δ x ) − Δ f ( x 0 ) \Delta^2 f\left(x_0\right)=\Delta f\left(x_0+\Delta x\right)-\Delta f\left(x_0\right) Δ2f(x0)=Δf(x0+Δx)−Δf(x0) ,也称为二阶差分 (为一阶差分的差分) Δ 3 f ( x 0 ) = Δ 2 f ( x 0 + Δ x ) − Δ 2 f ( x 0 ) \Delta^3 f\left(x_0\right)=\Delta^2 f\left(x_0+\Delta x\right)-\Delta^2 f\left(x_0\right) Δ3f(x0)=Δ2f(x0+Δx)−Δ2f(x0) ,也称为三阶差分。做了这些假设之后我们来看看之前提到的 b 1 b_1 b1 会变成什么样子:
b 1 = f ( x 1 ) − f ( x 0 ) x 1 − x 0 ⟹ b 1 = Δ f ( x 0 ) Δ x b_1=\frac{f\left(x_1\right)-f\left(x_0\right)}{x_1-x_0} \Longrightarrow b 1=\frac{\Delta f\left(x_0\right)}{{\Delta x}} b1=x1−x0f(x1)−f(x0)⟹b1=ΔxΔf(x0)
而 f 1 ( x ) f_1(x) f1(x) 会变成:
f 1 ( x ) = f ( x 0 ) + f ( x 1 ) − f ( x 0 ) x 1 − x 0 ( x − x 0 ) ⟹ f 1 ( x ) = f ( x 0 ) + Δ f ( x 0 ) Δ x ( x − x ) f_1(x)=f\left(x_0\right)+\frac{f\left(x_1\right)-f\left(x_0\right)}{x_1-x_0}\left(x-x_0\right) \Longrightarrow f_1(x)=f\left(x_0\right)+\frac{\Delta f\left(x_0\right)}{\Delta x}(x-x) f1(x)=f(x0)+x1−x0f(x1)−f(x0)(x−x0)⟹f1(x)=f(x0)+ΔxΔf(x0)(x−x)同样的 f 2 ( x ) f_2(x) f2(x) 就变成了:
f 2 ( x ) = f ( x 0 ) + Δ f ( x 0 ) Δ x 0 ( x − x 0 ) + Δ 2 f ( x 0 ) 2 ( Δ x ) 2 ( x − x 0 ) ( x − x 1 ) Δ 2 f ( x 0 ) = Δ f ( x 0 + Δ x ) − Δ f ( x 0 ) = f ( x 0 + 2 Δ x ) − f ( x 0 + Δ x ) − [ f ( x 0 + Δ x ) − f ( x 0 ) ] f_2(x)=f\left(x_0\right)+\frac{\Delta f\left(x_0\right)}{\Delta x_0}\left(x-x_0\right)+\frac{\Delta^2 f\left(x_0\right)}{2 (\Delta x)^2}\left(x-x_0\right)\left(x-x_1\right)\\ \Delta^2 f\left(x_0\right)=\Delta f(x_0+\Delta x)- \Delta f(x_0)=f(x_0+2\Delta x)-f(x_0+\Delta x)-[f(x_0+\Delta x)-f(x_0 )] f2(x)=f(x0)+Δx0Δf(x0)(x−x0)+2(Δx)2Δ2f(x0)(x−x0)(x−x1)Δ2f(x0)=Δf(x0+Δx)−Δf(x0)=f(x0+2Δx)−f(x0+Δx)−[f(x0+Δx)−f(x0)]泰勒断言,当 Δ x = 0 \Delta x=0 Δx=0 时:
f 1 ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) f 1 ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 \begin{gathered} f_1(x)=f\left(x_0\right)+f^{\prime}\left(x_0\right)\left(x-x_0\right) \\ f_1(x)=f\left(x_0\right)+f^{\prime}\left(x_0\right)\left(x-x_0\right)+\frac{f^{\prime \prime}\left(x_0\right)}{2 !}\left(x-x_0\right)^2 \end{gathered} f1(x)=f(x0)+f′(x0)(x−x0)f1(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2
( Δ x = 0 \left(\Delta x=0\right. (Δx=0 时由于 x 1 = x 0 + Δ x x_1=x_0+\Delta x x1=x0+Δx有 x − x 1 = x − x 0 ) \left.x-x_1=x-x_0\right) x−x1=x−x0)
以此类推泰勒就得到了大名鼎鼎的泰勒公式:
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + ⋯ f(x)=f\left(x_0\right)+f^{\prime}\left(x_0\right)\left(x-x_0\right)+\frac{f^{\prime \prime}\left(x_0\right)}{2 !}\left(x-x_0\right)^2+\cdots f(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+⋯
梯度下降法
梯度下降法其实可以泰勒公式来表示。假设要最小化损失函数L(w), 我们知道,梯度下降法的过程为:
- 选取初始值 w 0 w^0 w0
- 迭代更新 w t + 1 = w t − η L ′ ( w ) w^{t+1}=w^{t}-\eta L^{\prime}(w) wt+1=wt−ηL′(w),其中 η 为学习率 \eta 为学习率 η为学习率, w t + 1 w^{t+1} wt+1表示第t轮迭代得到的参数
用泰勒公式在 w t w^t wt处一阶展开则可以表示为
L ( w t + 1 ) = L ( w t ) + L ′ ( w t ) ( w t + 1 − w t ) + R ≈ L ( w t ) + L ′ ( w t ) ( w t + 1 − w t ) = L ( w t ) + η v L ′ ( w t ) \begin{aligned} L\left(w^{t+1}\right) & =L\left(w^t\right)+L^{\prime}\left(w^t\right)\left(w^{t+1}-w^t\right)+R \\ & \approx L\left(w^t\right)+L^{\prime}\left(w^t\right)\left(w^{t+1}-w^t\right) \\ & =L\left(w^t\right)+\eta v L^{\prime}\left(w^t\right) \end{aligned} L(wt+1)=L(wt)+L′(wt)(wt+1−wt)+R≈L(wt)+L′(wt)(wt+1−wt)=L(wt)+ηvL′(wt)
其中: R R R 为残差项,当 ( w t + 1 − w t ) \left(w^{t+1}-w^t\right) (wt+1−wt) 较小的时候, R ≈ 0 R \approx 0 R≈0设 w t + 1 − w t = η v , η w^{t+1}-w^t=\eta v, \eta wt+1−wt=ηv,η 为学习率, v v v 则为单位向量要使得迭代后损失函数变小,即 L ( w t + 1 ) < L ( w t ) L\left(w^{t+1}\right)<L\left(w^t\right) L(wt+1)<L(wt) ,回想向量相乘的公式, ∥ v ∥ ⋅ ∥ L ′ ( w t ) ∥ ⋅ cos θ \|v\| \cdot\left\|L^{\prime}\left(w^t\right)\right\| \cdot \cos \theta ∥v∥⋅∥L′(wt)∥⋅cosθ ,则我们可以令 v \mathrm{v} v 和 L ′ ( w t ) L^{\prime}\left(w^t\right) L′(wt) 反向,这样可以让他们向量乘积最小,于是
v = − L ′ ( w t ) ∥ L ′ ( w t ) ∥ v=-\frac{L^{\prime}\left(w^t\right)}{\left\|L^{\prime}\left(w^t\right)\right\|} v=−∥L′(wt)∥L′(wt)于是
w t + 1 = w t − η L ′ ( w t ) ∥ L ′ ( w t ) ∥ w^{t+1}=w^t-\eta \frac{L^{\prime}\left(w^t\right)}{\left\|L^{\prime}\left(w^t\right)\right\|} wt+1=wt−η∥L′(wt)∥L′(wt)又因为 ∥ L ′ ( w t ) ∥ \left\|L^{\prime}\left(w^t\right)\right\| ∥L′(wt)∥ 为标量,可以并入 η \eta η 中,即简化为:
w t + 1 = w t − η L ′ ( w t ) w^{t+1}=w^t-\eta L^{\prime}\left(w^t\right) wt+1=wt−ηL′(wt)
牛顿法
牛顿法其实是泰勒公式在
w
t
w^t
wt 处二阶展开,即
L
(
w
t
+
1
)
≈
L
(
w
t
)
+
L
′
(
w
t
)
(
w
t
+
1
−
w
t
)
+
L
′
′
(
w
t
)
2
(
w
t
+
1
−
w
t
)
2
L\left(w^{t+1}\right) \approx L\left(w^t\right)+L^{\prime}\left(w^t\right)\left(w^{t+1}-w^t\right)+\frac{L^{\prime \prime}\left(w^t\right)}{2}\left(w^{t+1}-w^t\right)^2
L(wt+1)≈L(wt)+L′(wt)(wt+1−wt)+2L′′(wt)(wt+1−wt)2
假设参数
w
w
w=
(
w
1
,
w
2
,
.
.
.
,
w
t
,
.
.
)
T
(w^1,w^2,...,w^t,..)^T
(w1,w2,...,wt,..)T 为一维向量,若
L
(
w
t
+
1
)
L\left(w^{t+1}\right)
L(wt+1) 为极小值,必然有其一阶导数为 0 ,因此可以让
L
L
L 对
w
t
+
1
w^{t+1}
wt+1 求偏导得
∂
L
∂
w
t
+
1
=
L
′
(
w
t
)
+
(
w
t
+
1
−
w
t
)
L
′
′
(
w
t
)
\frac{\partial L}{\partial w^{t+1}}=L^{\prime}\left(w^t\right)+\left(w^{t+1}-w^t\right) L^{\prime \prime}\left(w^t\right)
∂wt+1∂L=L′(wt)+(wt+1−wt)L′′(wt)
令偏导为 0 ,可得:
w
t
+
1
=
w
t
−
L
′
(
w
t
)
L
′
′
(
w
t
)
w^{t+1}=w^t-\frac{L^{\prime}\left(w^t\right)}{L^{\prime \prime}\left(w^t\right)}
wt+1=wt−L′′(wt)L′(wt)
如果扩展到高维,即w为向量,则
w
t
+
1
=
w
t
−
H
−
1
g
H
为海森矩阵,
g
=
L
′
(
w
t
)
w^{t+1}=w^t-H^{-1} g \quad H \text { 为海森矩阵, } g=L^{\prime}\left(w^t\right)
wt+1=wt−H−1gH 为海森矩阵, g=L′(wt)
牛顿法和梯度下降法对比
梯度下降法只利用到了目标函数的一阶偏导数信息,以负梯度方向作为搜索方向,只考虑目标函数在迭代点的局部性质。
而牛顿法不仅使用目标函数的一阶偏导数,还进一步利用了目标函数的二阶偏导数,这样就考虑了梯度变化的趋势,因而能更全面的确定合适的搜索方向以加快收敛。但牛顿法主要有一下两个缺点:
- 对目标函数有严格的要求,函数必须有连续的一、二阶偏导(二阶泰勒展开要求该区间内存在连续二阶导数,同时二阶泰勒展开会用一阶导,所以也要求一阶偏导数连续,否则二阶导数无法求极限),海森矩阵必须正定(一个矩阵是正定的,意味着对于所有非零向量x,都有 x T H x > 0 x^THx>0 xTHx>0。在优化问题中,这表明函数在该点附近是凸的,即该点是局部极小值)。
- 计算相当复杂,除需计算梯度以外,还需计算二阶偏导数矩阵和它的逆矩阵,计算量和空间消耗比较大。
XGBoost
在有监督学习中,可以分为:模型,参数 、目标函数和学习方法。
模型即给定输入xi如何预测输出yi,而这个y可以很多种形式,如回归,概率,类别、排序等
参数即比如线性回归的w
目标函数可以分为损失函数+正则: Obj ( Θ ) = L ( Θ ) + Ω ( Θ ) \operatorname{Obj}(\Theta)=L(\Theta)+\Omega(\Theta) Obj(Θ)=L(Θ)+Ω(Θ)
损失函数:如平方误差等,告诉我们模型拟合数据的情况。 => Bias
正则项:惩罚复杂的模型,鼓励简单的模型。 => Variance
L1正则化通过惩罚模型参数的绝对值来工作。这导致模型参数中的一些变成零,从而产生一个稀疏模型。通过减少模型中非零参数的数量,L1正则化可以减少模型的复杂性和方差;L2正则化通过惩罚模型参数的平方和来工作。这种方法倾向于均匀地减小所有参数的值[5** 2减小为2**2】,从而使模型变得不那么敏感于输入数据的小波动,降低了方差)
模型学习方法即解决给定目标函数后怎么学的问题。
在XGBoost中:
-
模型学习:定义目标函数,然后优化目标函数
-
目标函数(XGBoost中目标函数是针对一棵树的目标函数,而不是针对一个样本或一整个算法的目标函数。并且,任意树的目标函数都包括三大部分:损失函数 l l l、叶子数量 T T T以及正则项): Obj ( Θ ) = ∑ i = 1 N l ( y i , y ^ i ) + ∑ j = 1 t Ω ( f j ) , f j ∈ F \operatorname{Obj}(\Theta)=\sum_{i=1}^N l\left(y_i, \hat{y}_i\right)+\sum_{j=1}^t \Omega\left(f_j\right), \quad f_j \in \mathcal{F} Obj(Θ)=∑i=1Nl(yi,y^i)+∑j=1tΩ(fj),fj∈F
由于f是树,而不是连续数值型的向量,所以不能用梯度下降法,可以通过前向分步算法,即贪心法找到局部最优解: y ^ i ( t ) = ∑ j = 1 t f j ( x i ) = y ^ i ( t − 1 ) + f t ( x i ) \hat{y}_i^{(t)}=\sum_{j=1}^t f_j\left(x_i\right)=\hat{y}_i^{(t-1)}+f_t\left(x_i\right) y^i(t)=∑j=1tfj(xi)=y^i(t−1)+ft(xi)
所以目标函数可以写成
O b j ( t ) = ∑ i = 1 N l ( y i , y ^ i ( t ) ) + ∑ j = 1 t Ω ( f j ) = ∑ i = 1 N l ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) + Ω ( f t ) + constant ≈ ∑ i = 1 N l ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) + Ω ( f t ) \begin{aligned} O b j^{(t)} & =\sum_{i=1}^N l\left(y_i, \hat{y}_i^{(t)}\right)+\sum_{j=1}^t \Omega\left(f_j\right) \\ & =\sum_{i=1}^N l\left(y_i, \hat{y}_i^{(t-1)}+f_t\left(\mathbf{x}_{\mathbf{i}}\right)\right)+\Omega\left(f_t\right)+\text { constant }\\ &\approx \sum_{i=1}^{N}l\left(y_i, \hat{y}_i^{(t-1)}+f_t\left(\mathbf{x}_{\mathbf{i}}\right)\right)+\Omega\left(f_t\right) \end{aligned} Obj(t)=i=1∑Nl(yi,y^i(t))+j=1∑tΩ(fj)=i=1∑Nl(yi,y^i(t−1)+ft(xi))+Ω(ft)+ constant ≈i=1∑Nl(yi,y^i(t−1)+ft(xi))+Ω(ft)
第t轮训练时,前面的t-1轮的正则项都相当于常数,可以不做考虑,但是损失函数不满足 l ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) = l ( y i , y ^ i ( t − 1 ) ) + l ( y i , f t ( x i ) ) l(y_i, \hat y_i^{(t-1)}+f_t(x_i))=l(y_i, \hat y_i^{(t-1)})+l(y_i,f_t(x_i)) l(yi,y^i(t−1)+ft(xi))=l(yi,y^i(t−1))+l(yi,ft(xi))
假设损失函数使用的是平方损失,则上式可以写成
O b j ( t ) = ∑ i = 1 N ( y i − ( y ^ i ( t − 1 ) + f t ( x i ) ) ) 2 + Ω ( f t ) = ∑ i = 1 N ( y i − y ^ i ( t − 1 ) ⏟ 残差 − f t ( x i ) ) 2 + Ω ( f t ) \begin{aligned} O b j^{(t)} & =\sum_{i=1}^N\left(y_i-\left(\hat{y}_i^{(t-1)}+f_t\left(\mathbf{x}_{\mathbf{i}}\right)\right)\right)^2+\Omega\left(f_t\right) \\ & =\sum_{i=1}^N(\underbrace{y_i-\hat{y}_i^{(t-1)}}_{\text {残差 }}-f_t\left(\mathbf{x}_{\mathbf{i}}\right))^2+\Omega\left(f_t\right)\end{aligned} Obj(t)=i=1∑N(yi−(y^i(t−1)+ft(xi)))2+Ω(ft)=i=1∑N(残差 yi−y^i(t−1)−ft(xi))2+Ω(ft)
对于一般的损失函数,可以对目标函数进行二阶泰勒展开
O b j ( t ) = ∑ i = 1 N l ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) + Ω ( f t ) = ∑ i = 1 N ( l ( y i , y ^ i ( t − 1 ) ) + g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ) + Ω ( f t ) 其中, g i = ∂ l ( y i , y ^ i ) ∂ y ^ i ∣ y ^ i = y ^ i ( t − 1 ) , h i = ∂ 2 l ( y i , y ^ i ) ∂ 2 y ^ i ∣ y ^ i = y ^ i ( t − 1 ) \begin{aligned} O b j^{(t)} & =\sum_{i=1}^N l\left(y_i, \hat{y}_i^{(t-1)}+f_t\left(\mathbf{x}_{\mathbf{i}}\right)\right)+\Omega\left(f_t\right) \\ & =\sum_{i=1}^N\left(l\left(y_i, \hat{y}_i^{(t-1)}\right)+g_i f_t\left(\mathbf{x}_{\mathbf{i}}\right)+\frac{1}{2} h_i f_t^2\left(\mathbf{x}_{\mathbf{i}}\right)\right)+\Omega\left(f_t\right) \\ & \text { 其中, } g_i=\frac{\partial l\left(y_i, \hat{y}_i\right)}{\partial \hat{y}_i}|_{\hat{y}_i=\hat{y}_i^{(t-1)}}, h_i=\frac{\partial^2 l\left(y_i, \hat{y}_i\right)}{\partial^2 \hat{y}_i}|_{\hat{y}_i=\hat{y}_i^{(t-1)}}\end{aligned} Obj(t)=i=1∑Nl(yi,y^i(t−1)+ft(xi))+Ω(ft)=i=1∑N(l(yi,y^i(t−1))+gift(xi)+21hift2(xi))+Ω(ft) 其中, gi=∂y^i∂l(yi,y^i)∣y^i=y^i(t−1),hi=∂2y^i∂2l(yi,y^i)∣y^i=y^i(t−1)
-
正则项:
-
XGBoost采用衡量树复杂度的方式为:一棵树里面叶子节点的个数T,以及每棵树叶子节点上面输出分数w的平方和(相当于L2正则)
Ω ( f t ) = γ T + 1 2 λ ∑ j = 1 T w j 2 \Omega\left(f_t\right)=\gamma T+\frac{1}{2} \lambda \sum_{j=1}^T w_j^2 Ω(ft)=γT+21λ∑j=1Twj2
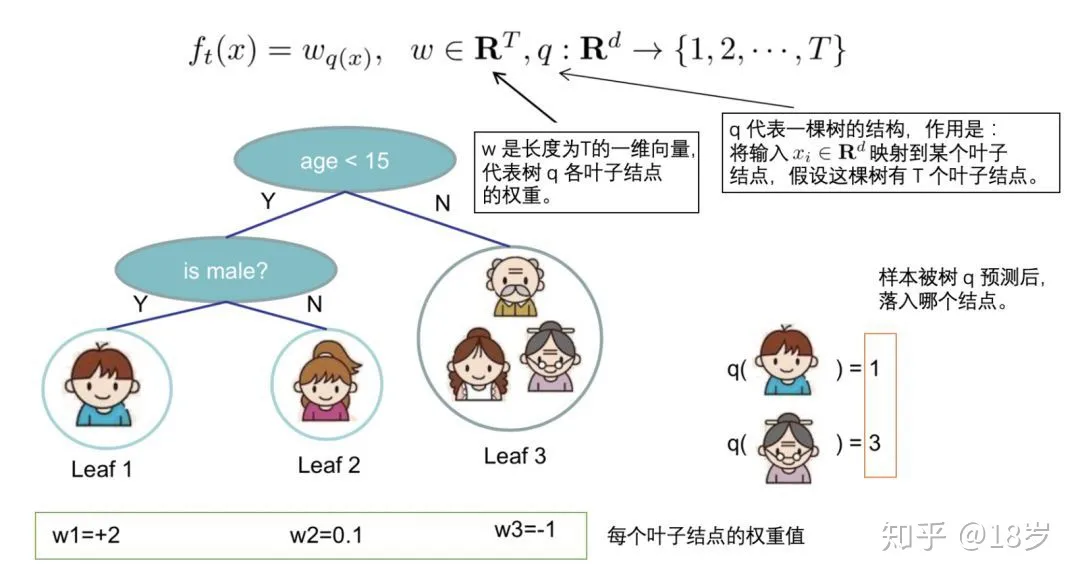
将损失函数和正则项结合得到 O b j ( t ) = ∑ i = 1 N ( g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ) ⏟ 对样本累加 + γ T + 1 2 λ ∑ j = 1 T w j 2 ⏟ 对叶结点累加 O b j^{(t)}=\underbrace{\sum_{i=1}^N\left(g_i f_t\left(\mathbf{x}_{\mathbf{i}}\right)+\frac{1}{2} h_i f_t^2\left(\mathbf{x}_{\mathbf{i}}\right)\right)}_{\text {对样本累加 }}+\gamma T+\frac{1}{2} \lambda \underbrace{\sum_{j=1}^T w_j^2}_{\text {对叶结点累加 }} Obj(t)=对样本累加 i=1∑N(gift(xi)+21hift2(xi))+γT+21λ对叶结点累加 j=1∑Twj2
前后求和符合上下限要保持一致,将各个样本的损失函数映射到各个叶节点上,此处定义q函数将输入x映射到某个叶节点上,即
f t ( x ) = w q ( x ) ( 表示树各叶子结点的权重 ) ,把 x 看成一个向量 ) ,同时定义每个叶子节点 j 上的样本集合 ( 样本 x i 在第 j 个叶子节点上 ) 为 I j = { i ∣ q ( x i ) = j } f_t(x)=w_{q(x)}(表示树各叶子结点的权重),把x看成一个向量),同时定义每个叶子节点j上的样本集合(样本x_i在第j个叶子节点上)为\\I_j=\left\{i \mid q\left(x_i\right)=j\right\} ft(x)=wq(x)(表示树各叶子结点的权重),把x看成一个向量),同时定义每个叶子节点j上的样本集合(样本xi在第j个叶子节点上)为Ij={i∣q(xi)=j}
则目标函数可以写成
O b j ( t ) = ∑ i = 1 N ( g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ) + γ T + 1 2 λ ∑ j = 1 T w j 2 = ∑ i = 1 N ( g i w q ( x i ) + 1 2 h i w q ( x i ) 2 ) + γ T + 1 2 λ ∑ j = 1 T w j 2 = ∑ j = 1 T ( ∑ i ∈ I j g i w j + 1 2 ∑ i ∈ I j h i w j 2 ) + γ T + 1 2 λ ∑ j = 1 T w j 2 = ∑ j = 1 T ( G j w j + 1 2 ( H j + λ ) w j 2 ) + γ T \begin{aligned} O b j^{(t)} & =\sum_{i=1}^N\left(g_i f_t\left(\mathbf{x}_{\mathbf{i}}\right)+\frac{1}{2} h_i f_t^2\left(\mathbf{x}_{\mathbf{i}}\right)\right)+\gamma T+\frac{1}{2} \lambda \sum_{j=1}^T w_j^2 \\ & =\sum_{i=1}^N\left(g_i w_{q\left(\mathbf{x}_{\mathbf{i}}\right)}+\frac{1}{2} h_i w_{q\left(\mathbf{x}_{\mathbf{i}}\right)}^2\right)+\gamma T+\frac{1}{2} \lambda \sum_{j=1}^T w_j^2 \\ & =\sum_{j=1}^T\left(\sum_{i \in I_j} g_i w_j+\frac{1}{2} \sum_{i \in I_j} h_i w_j^2\right)+\gamma T+\frac{1}{2} \lambda \sum_{j=1}^T w_j^2 \\ & =\sum_{j=1}^T\left(G_j w_j+\frac{1}{2}\left(H_j+\lambda\right) w_j^2\right)+\gamma T\end{aligned} Obj(t)=i=1∑N(gift(xi)+21hift2(xi))+γT+21λj=1∑Twj2=i=1∑N(giwq(xi)+21hiwq(xi)2)+γT+21λj=1∑Twj2=j=1∑T i∈Ij∑giwj+21i∈Ij∑hiwj2 +γT+21λj=1∑Twj2=j=1∑T(Gjwj+21(Hj+λ)wj2)+γT
其中 G j = ∑ i ∈ I j g i , H j = ∑ i ∈ I j h i G_j=\sum_{i \in I_j}g_i, H_j=\sum_{i \in I_j}h_i Gj=∑i∈Ijgi,Hj=∑i∈Ijhi
-
现在要做的是两件事:
- 确定树的结构, 这样这一轮的目标函数(也就是变量T)就确定了下来;
- 求使得当前这一轮(第t轮)的目标函数最小的叶结点分数w。(Obj代表了当我们指定一个树的结构的时候,我们在目标上面最多减少多少,也称为结构分数,structure score)
假设已经知道了树的结构,那么第2件事情是十分简单的,直接对w求导,使得导数为0,就得到每个叶结点的预测分数为:
w
j
=
−
b
2
a
=
−
G
j
H
j
+
λ
,
则此时目标函数取到最小值
w_j=-\frac{b}{2a}=-\frac{G_j}{H_j+ \lambda},则此时目标函数取到最小值
wj=−2ab=−Hj+λGj,则此时目标函数取到最小值
O
b
j
(
t
)
=
∑
j
=
1
T
(
G
j
w
j
+
1
2
(
H
j
+
λ
)
w
j
2
)
+
γ
T
=
∑
j
=
1
T
(
−
G
j
2
H
j
+
λ
+
1
2
G
j
2
H
j
+
λ
)
+
γ
T
=
−
1
2
∑
j
=
1
T
(
G
j
2
H
j
+
λ
)
+
γ
T
\begin{aligned} O b j^{(t)} & =\sum_{j=1}^T\left(G_j w_j+\frac{1}{2}\left(H_j+\lambda\right) w_j^2\right)+\gamma T \\ & =\sum_{j=1}^T\left(-\frac{G_j^2}{H_j+\lambda}+\frac{1}{2} \frac{G_j^2}{H_j+\lambda}\right)+\gamma T \\ & =-\frac{1}{2} \sum_{j=1}^T\left(\frac{G_j^2}{H_j+\lambda}\right)+\gamma T \end{aligned}
Obj(t)=j=1∑T(Gjwj+21(Hj+λ)wj2)+γT=j=1∑T(−Hj+λGj2+21Hj+λGj2)+γT=−21j=1∑T(Hj+λGj2)+γT

总结推导流程

基本流程分析:
假设现有数据集 N N N,含有形如 ( x i , y i ) (x_i,y_i) (xi,yi)的样本 M M M个, i i i为任意样本的编号,单一样本的损失函数为 l ( y i , H ( x i ) ) l(y_i,H(x_i)) l(yi,H(xi)),其中 H ( x i ) H(x_i) H(xi)是 i i i号样本在集成算法上的预测结果,整个算法的损失函数为 L ( y , H ( x ) ) L(y,H(x)) L(y,H(x)),且总损失等于全部样本的损失之和: L ( y , H ( x ) ) = ∑ i l ( y i , H ( x i ) ) L(y,H(x)) = \sum_i l(y_i,H(x_i)) L(y,H(x))=∑il(yi,H(xi))。目标函数中使用L2正则化( α \alpha α为0),并且 γ \gamma γ不为0。
同时,弱评估器为回归树 f f f,总共学习 K K K轮(注意在GBDT当中我们使用的是大写字母T来表示迭代次数,由于在XGBoost当中字母T被用于表示目标函数中的叶子总量,因此我们在这里使用字母K表示迭代次数)
-
1) 初始化
考虑到XGBoost在许多方面继承了梯度提升树GBDT的思想,我们可以使用公式来计算XGBoost的 H 0 H_0 H0:
H 0 ( x ) = a r g m i n C ∑ i = 1 M l ( y i , C ) = a r g m i n C L ( y , C ) \begin{aligned} H_0(x) &= \mathop{argmin}_{C} \sum_{i=1}^M l(y_i,C)\\ \\ &= \mathop{argmin}_{C} L(y,C) \end{aligned} H0(x)=argminCi=1∑Ml(yi,C)=argminCL(y,C)
开始循环,for k in 1,2,3…K:
-
2) 抽样
在现有数据集 N N N中,抽样 M M M *
subsample个样本,构成训练集 N k N^k Nk(subsample:抽样比) -
3) 求拟合项
对任意一个样本 i i i,计算一阶导数 g i k g_{ik} gik,二阶导数 h i k h_{ik} hik,以及伪残差(pseudo-residuals) r i k r_{ik} rik,具体公式为:
g i k = ∂ l ( y i , H ( x i ) ) ∂ H ( x i ) ∣ H ( x i ) = H k − 1 ( x i ) g_{ik} = \frac{\partial{l(y_i,H(x_i))}}{\partial{H(x_i)}}|_{H(x_i)=H_{k-1}(x_i)} gik=∂H(xi)∂l(yi,H(xi))∣H(xi)=Hk−1(xi)
h i k = ∂ 2 l ( y i , H ( x i ) ) ∂ H 2 ( x i ) ∣ H ( x i ) = H k − 1 ( x i ) h_{ik} = \frac{\partial^2{l(y_i,H(x_i))}}{\partial{H^2(x_i)}}|_{H(x_i)=H_{k-1}(x_i)} hik=∂H2(xi)∂2l(yi,H(xi))∣H(xi)=Hk−1(xi)
r i k = − g i k h i k r_{ik} = -\frac{g_{ik}}{h_{ik}} rik=−hikgik
证明 r i k r_{ik} rik:
∑ i = 1 N ( g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ) + Ω ( f t ) = ∑ i = 1 N 1 2 h i ( 2 g i h i f t ( x i ) + f t 2 ( x i ) ) + Ω ( f t ) = ∑ i = 1 N 1 2 h i ( g i 2 h i 2 + 2 g i h i f t ( x i ) + f t 2 ( x i ) ) + Ω ( f t ) = ∑ i = 1 N 1 2 h i ( f t ( x i ) − ( − g i h i ) ) 2 + Ω ( f t ) ( Ω 可忽略 , 下面会解释 ) \begin{aligned} & \sum_{i=1}^N\left(g_i f_t\left(\mathbf{x}_{\mathbf{i}}\right)+\frac{1}{2} h_i f_t^2\left(\mathbf{x}_{\mathbf{i}}\right)\right)+\Omega\left(f_t\right) \\ = & \sum_{i=1}^N \frac{1}{2} h_i\left(2 \frac{g_i}{h_i} f_t\left(\mathbf{x}_{\mathbf{i}}\right)+f_t^2\left(\mathbf{x}_{\mathbf{i}}\right)\right)+\Omega\left(f_t\right) \\ = & \sum_{i=1}^N \frac{1}{2} h_i\left(\frac{g_i^2}{h_i^2}+2 \frac{g_i}{h_i} f_t\left(\mathbf{x}_{\mathbf{i}}\right)+f_t^2\left(\mathbf{x}_{\mathbf{i}}\right)\right)+\Omega\left(f_t\right) \\ = & \sum_{i=1}^N \frac{1}{2} h_i\left(f_t\left(\mathbf{x}_{\mathbf{i}}\right)-\left(-\frac{g_i}{h_i}\right)\right)^2+\Omega\left(f_t\right)(\Omega可忽略,下面会解释)\end{aligned} ===i=1∑N(gift(xi)+21hift2(xi))+Ω(ft)i=1∑N21hi(2higift(xi)+ft2(xi))+Ω(ft)i=1∑N21hi(hi2gi2+2higift(xi)+ft2(xi))+Ω(ft)i=1∑N21hi(ft(xi)−(−higi))2+Ω(ft)(Ω可忽略,下面会解释)目标函数 = ∑ j = 1 T ( w j ∑ i ∈ j g i + 1 2 w j 2 ( ∑ i ∈ j h i + λ ) ) + γ T \begin{aligned} 目标函数 &= \sum_{j=1}^T \left( \boldsymbol{\color{red}{w_j\sum_{i \in j} g_i + \frac{1}{2}w^2_j(\sum_{i \in j} h_i + \lambda)}} \right) + \gamma T\end{aligned} 目标函数=j=1∑T wji∈j∑gi+21wj2(i∈j∑hi+λ) +γT
将标注为红色的部分命名为 μ j \mu_j μj
对任意位于叶子 j j j上的样本 i i i来说:
μ i = w j g i + 1 2 w j 2 ( h i + λ ) \mu_i = w_jg_i + \frac{1}{2}w^2_j(h_i+\lambda) μi=wjgi+21wj2(hi+λ)
将一片叶子上的 μ j \mu_j μj转变成 μ i \mu_i μi(i:叶子节点上的某个样本)时,原则上需要将 μ j \mu_j μj中的每一项都转换为单个样本所对应的项,然而在转换正则项时则存在问题:与 ∑ i ∈ j g i \sum_{i \in j} g_i ∑i∈jgi(可以直接指向单个样本的项)不同, λ \lambda λ是针对与一片叶子设置的值,如果要将 λ \lambda λ转变为针对单一样本的正则项,则需要知道当前叶子上一共有多少样本。然而,拟合发生在建树之前(在算法流程中拟合步骤在建树步骤之前),因此在这一时间点不可能知道一片叶子上的样本总量,因此在xgboost的实际实现过程当中,拟合每一片叶子时不涉及正则项,只有在计算结构分数与叶子输出值时才使用正则项。
对 μ i \mu_i μi上唯一的自变量 w j w_j wj求导,则有:
∂ μ i ∂ w j = ∂ ( w j g i + 1 2 w j 2 h i ) ∂ w j = g i + w j h i \begin{aligned}\frac{\partial{\mu_i}}{\partial w_j} &= \frac{\partial{\left( w_jg_i + \frac{1}{2}w^2_jh_i \right)}}{\partial w_j} \\ \\ &= g_i + w_jh_i\end{aligned} ∂wj∂μi=∂wj∂(wjgi+21wj2hi)=gi+wjhi
令一阶导数为0,则有:
g i + w j h i = 0 w j h i = − g i w j = − g i h i \begin{aligned} g_i + w_jh_i &= 0 \\ \\ w_jh_i &= - g_i \\ \\ w_j &= -\frac{g_i}{h_i} \end{aligned} gi+wjhiwjhiwj=0=−gi=−higi
对任意样本 i i i而言,令目标函数最小的最优 w j w_j wj就是我们的伪残差 r i r_i ri,也就是XGBoost数学流程当中用于进行拟合的拟合值。
- 4) 建树
求解出伪残差后,在数据集
(
x
i
,
r
i
k
)
(x_i, r_{ik})
(xi,rik)上按colsample_by*(这个是sklearn的超参数,在xgboost代码章节中会讲到)规则进行抽样,再按照结构分数增益规则建立一棵回归树
f
k
f_k
fk。注意在这个过程中,训练时拟合的标签为样本的伪残差
r
i
k
r_{ik}
rik,并且叶子节点
j
j
j的结构分数和任意分枝时的结构分数增益的公式为:
S
c
o
r
e
j
=
(
∑
i
∈
j
g
i
)
2
∑
i
∈
j
h
i
+
λ
Score_j = \frac{(\sum_{i \in j}g_i)^2}{\sum_{i \in j}h_i + \lambda}
Scorej=∑i∈jhi+λ(∑i∈jgi)2
G a i n = 1 2 ( ( ∑ i ∈ L g i ) 2 ∑ i ∈ L h i + λ + ( ∑ i ∈ R g i ) 2 ∑ i ∈ R h i + λ − ( ∑ i ∈ P g i ) 2 ∑ i ∈ P h i + λ ) − γ Gain = \frac{1}{2} \left( \frac{(\sum_{i \in L}g_i)^2}{\sum_{i \in L}h_i + \lambda} + \frac{(\sum_{i \in R}g_i)^2}{\sum_{i \in R}h_i + \lambda} - \frac{(\sum_{i \in P}g_i)^2}{\sum_{i \in P}h_i + \lambda} \right) - \gamma Gain=21(∑i∈Lhi+λ(∑i∈Lgi)2+∑i∈Rhi+λ(∑i∈Rgi)2−∑i∈Phi+λ(∑i∈Pgi)2)−γ
建树过程不影响任何 g i k g_{ik} gik与 h i k h_{ik} hik的值。
- 5) 输出树上的结果
建树之后,依据回归树
f
k
f_k
fk的结构输出叶子节点上的输出值(预测值)。对任意叶子节点
j
j
j来说,输出值为:
w
j
=
−
∑
i
∈
j
g
i
k
∑
i
∈
j
h
i
k
+
λ
w_j = -\frac{\sum_{i \in j}g_{ik}}{\sum_{i \in j}h_{ik} + \lambda}
wj=−∑i∈jhik+λ∑i∈jgik
假设样本
i
i
i被分割到叶子
j
j
j上,则有:
f
k
(
x
i
)
=
w
j
f_k(x_i) = w_j
fk(xi)=wj
思考:在迭代刚开始时我们已经知道了输出值式子中所需的所有 g g g和 h h h。为什么还要建树呢?
只有当我们建立了决策树,我们才能够知道具体哪些样本 i i i在叶子节点 j j j上。因此树 f k f_k fk提供的是结构信息。
-
6) 迭代
根据预测结果 f k ( x i ) f_k(x_i) fk(xi)迭代模型,具体来说:
H k ( x i ) = H k − 1 ( x i ) + f k ( x i ) H_k(x_i) = H_{k-1}(x_i) + f_k(x_i) Hk(xi)=Hk−1(xi)+fk(xi)
假设输入的步长为 η \eta η,则 H k ( x ) H_k(x) Hk(x)应该为:
H k ( x i ) = H k − 1 ( x i ) + η f k ( x i ) H_k(x_i) = H_{k-1}(x_i) + \eta f_k(x_i) Hk(xi)=Hk−1(xi)+ηfk(xi)
对整个算法则有:
H k ( x ) = H k − 1 ( x ) + η f k ( x ) H_k(x) = H_{k-1}(x) + \eta f_k(x) Hk(x)=Hk−1(x)+ηfk(x) -
7) 循环结束
输出 H K ( x ) H_K(x) HK(x)的值作为集成模型的输出值。
参考资料:
- https://www.matongxue.com/madocs/7/
- https://www.matongxue.com/madocs/126/
- 菜菜九天机器学习课程
- https://www.hrwhisper.me/machine-learning-xgboost/


























 108
108











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








