熵权法原理以及代码

1.熵权法基本原理

在信息论中，熵是对不确定性的一种度量。不确定性越大，熵就越大，包含的信息量越大；不确定性越小，熵就越小，包含的信息量就越小。

根据熵的特性，可以通过计算熵值来判断一个事件的随机性以及无序程度，也可以用熵值来判断某个指标的离散程度，指标的离散程度越大，该指标对综合评价的影响（权重越大）。比如样本数据在某指标下取值都相等，则该指标对总体评价的影响为0，权值为0.

熵权法是一种客观赋权法，因为它仅依赖于数据本身的离散性。

2.熵权法步骤

1.对n个样本，m个指标，则为第i个样本的第j个指标的数值(i=1,...,n; j=1,...,m);

2.指标的归一化处理：异质指标同质化

由于各项指标的计量单位并不统一，因此在用它们计算综合指标前，先要进行标准化处理，即把指标的绝对值转化为相对值，从而解决各项不同质指标值的同质化问题。

另外，正向指标和负向指标数值代表的含义不同(正向指标数值越高越好，负向指标数值越低越好)，因此，对于正向负向指标需要采用不同的算法进行数据标准化处理:

 为了方便起见，归一化后的数据仍记为

 

3.计算第j项指标下第i个样本值占该指标的比重；

4.计算第j项指标的熵值：

 

 

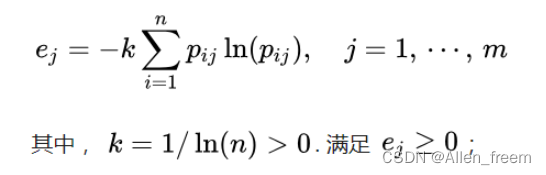
5.计算信息熵冗余度（差异）：

=1- , j=1,...,m

6.计算该项指标的权重：

 

7.计算各样本的综合得分：

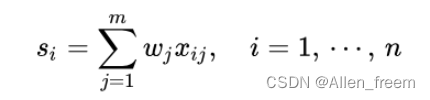
其中，为标准化后的数据。

3.Matlab实现

归一：

function y=guiyi(x,type,ymin,ymax)
%实现正向或负向指标归一化，返回归一化后的数据矩阵
%x为原始数据矩阵, 一行代表一个样本, 每列对应一个指标
%type设定正向指标1,负向指标2
%ymin,ymax为归一化的区间端点
[n,m]=size(x);
y=zeros(n,m);
xmin=min(x);
xmax=max(x);
switch type
    case 1
        for j=1:m
            y(:,j)=(ymax-ymin)*(x(:,j)-xmin(j))/(xmax(j)-xmin(j))+ymin;
        end
    case 2
        for j=1:m
            y(:,j)=(ymax-ymin)*(xmax(j)-x(:,j))/(xmax(j)-xmin(j))+ymin;
        end
end

 

Main：

 

load shang_datas

Ind=[1 1 1 1 2]; %指定各指标的正向or负向

[S,W]=shang(shang_datas,Ind)

熵权法：

function [s,w]=shang(x,ind)
%实现用熵值法求各指标(列）的权重及各数据行的得分
%x为原始数据矩阵, 一行代表一个样本, 每列对应一个指标
%ind指示向量，指示各列正向指标还是负向指标，1表示正向指标，2表示负向指标
%s返回各行（样本）得分，w返回各列权重
[n,m]=size(x); % n个样本, m个指标
%%数据的归一化处理
for i=1:m
    if ind(i)==1 %正向指标归一化
        X(:,i)=guiyi(x(:,i),1,0.002,0.996);    %若归一化到[0,1], 0会出问题
    else %负向指标归一化
        X(:,i)=guiyi(x(:,i),2,0.002,0.996);
    end
end
%%计算第j个指标下，第i个样本占该指标的比重p(i,j)
for i=1:n
    for j=1:m
        p(i,j)=X(i,j)/sum(X(:,j));
    end
end
%%计算第j个指标的熵值e(j)
k=1/log(n);
for j=1:m
    e(j)=-k*sum(p(:,j).*log(p(:,j)));
end
d=ones(1,m)-e; %计算信息熵冗余度
w=d./sum(d); %求权值w
s=100*w*X'; %求综合得分

4.熵权法的优缺点：

优点：

• 熵权法能深刻反应指标的区分能力，确定较好的权重
• 赋权更加客观，有理论依据，可信度也更加高
• 算法简单，实践，不需要其他软件分析

缺点：

• 无法考虑到指标与指标之间的横向影响
• 对样本依赖性大，随建模样本变化，权重也会发生变化
• 可能导致权重失真，最终结果无效。