函数性质探究（一对一、介质性、连续性、单调性之间的关系）

题面：

探究一 ：能否由介值性和一一对应，推出函数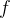的单调性？

给出以下命题:

分析：

只需证明一种情况，另一种情况同理。结合介值性，利用反证法.

证明： 

反思：

由反函数的定义，在（，）上严格单调，则在（，）上是一对一的

那么能否只由一对一的性质，推断出是严格单调的？

答案是否定的，我们可以构造反例

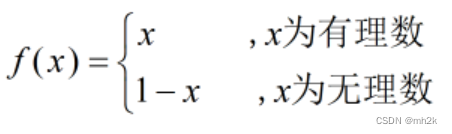
在 （0，1）上的反函数为本身，是一对一的，但不单调，也无介值性

 探究二 ：能否由介值性和一一对应，推出函数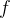的连续性？

给出以下命题:

 分析：

延续证单调性的思路，假设不连续，结合介值性，产生不一一对应的矛盾.

 证明：

反思：

 我们可以很容易的找出反例，在（，）上是一对一的但不连续(如上一个反思的例子)

那么能否只由的介值性，推断出是连续的？ 

答案是否定的， 由Darboux定理可知导函数有介值性但不一定连续，以下是经典反例：

探究三： 介值性未知，单调性与连续性互证

一一对应+严格单调证明连续性： 

虽然介值性未知，但该证明以的值域为某个开区间为前提，否则逆映射可能为空集

证明： 

 一一对应+连续性证明严格单调：

只需证明连续函数一定有介值性，沿用之前证明思路即可.

 命题：

分析： 

证明： 

思考 ：

证明过程中的为何要充分小？

因S可能是间断的，见如下草图

 

证明了闭区间上的连续函数的介值性后，可推广得到开区间上的介值性：

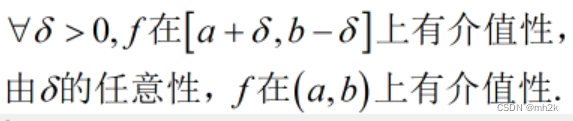
探究四：反函数是否也满足以上性质？

反函数的单调性，介值性：

反函数的连续性：

反函数的连续性证明与由单调性证明原函数连续性同理.

总结：