“Xavier”初始化方法是一种很有效的神经网络初始化方法,方法来源于2010年的一篇论文《Understanding the difficulty of training deep feedforward neural networks》,可惜直到近两年,这个方法才逐渐得到更多人的应用和认可。
xavier
xavier诞生时并没有用relu做例子,但是实际效果中xavier还是和relu很搭配的。xavier是如何完成初始化工作的呢?它的初始化公式如下所示:
定义参数所在层的输入维度为n,输出维度为m,那么参数将以均匀分布的方式在![[-\sqrt{\frac{6}{m+n}},\sqrt{\frac{6}{m+n}}]](https://i-blog.csdnimg.cn/blog_migrate/926c96daf581dc66fe5e7a8a165de48f.png) 的范围内进行初始化。
的范围内进行初始化。
那么这个公式是如何计算出来的呢?关于这个问题我们需要一段漫长的推导。在推导之前我们要强调一个关键点,就是参数的标准差,或者方差。前面我们提到了Caffe中的debug_info主要展示了数据的L1 norm,对于均值为0的数据来说,这个L1 norm可以近似表示标准差。
我们将用到以下和方差相关的定理:
假设有随机变量x和w,它们都服从均值为0,方差为 的分布,那么:
的分布,那么:
- w*x就会服从均值为0,方差为
 的分布
的分布
- w*x+w*x就会服从均值为0,方差为
 的分布
的分布
以下内容主要来自论文《Understanding the difficulty of training deep feedforward neural network》的理解,这里将以我个人的理解做一下解读,如果有错欢迎来喷。
前面两个定理的变量名称是不是有点熟悉?没错,下面我们说的就是参数w和x。这里暂时将偏置项放在一边,同时我们还要把一个部分放在一边,那就是非线性部分。这篇论文心目中的理想非线性函数是tanh。为啥呢?
在大神的假想世界中,x和w都是靠近0的比较小的数字,那么它们最终计算出来的数字也应该是一个靠近0,比较小的数字。如果数值集中在0附近,我们可以发现,前向时tanh靠近0的地方斜率接近1,所以前辈告诉我们,把它想象成一个线性函数。
下面这张梯度的图像也是一样,靠近0的地方斜率接近1,所以前辈又一次告诉我们,把它想象成一个线性函数。
什么,你不信?
把它想象成一个线性函数。
把它想象成一个线性函数。
把它想象成一个线性函数……
好了,现在这个挡在中间的非线性函数硬生生掰成一个线性函数了,为了理论的完美我们也是什么也不顾了。下面就要面对一个问题,如何让深层网络在学习过程中的表现像浅层网络?
我们的脑中迅速回忆起我们接触过的浅层模型——logistic regression,SVM。为了它们的表现能够更好,我们都会把特征做初始化,细心处理,比方说做白化处理,使他的均值方差保持好,然后用浅层模型一波训练完成。现在我们采用了深层模型,输入的第一层我们是可以做到数据的白化的——减去均值,除以一个标准差。但是里面层次的数据,你总不好伸手进入把它们也搞白化吧!(当然,后来真的有人伸进去了,还做得不错)那我们看看如果在中间层不做处理会发生什么?
我们假设所有的输入数据x满足均值为0,方差为的分布,我们再将参数w以均值为0,方差为
的方式进行初始化。我们假设第一次是大家喜闻乐见的卷积层,卷积层共有n个参数(n=channel*kernel_h*kernel_w),于是为了计算出一个线性部分的结果,我们有:

这个公式的下标不准确,大家姑且这么看了,也就是说,线性输出部分的一个结果值,实际上是由n个乘加计算出来的,那么下面是一道抢答题,按照我们刚才对x和w的定义,加上前面我们说过的两个方差计算公式,这个z会服从一个什么分布呢?
均值肯定还是0嘛,没得说。
方差好像积累了一大堆东西:
然后我们通过那个靠意念构建的具有“线性特征”的非线性层,奇迹般地发现一切都没有变化,那么下一层的数据就成了均值为0,方差为 的“随机变量”(姑且称之为随机变量吧)。
的“随机变量”(姑且称之为随机变量吧)。
为了更好地表达,我们将层号写在变量的上标处,于是就有:

我们将卷积层和全连接层统一考虑成n个参数的一层,于是接着就有:

如果我们是一个k层的网络(这里主要值卷积层+全连接层的总和数),我们就有

继续把这个公式展开,就会得到它的最终形态:

可以看出,后面的那个连乘实际上看着就像个定时炸弹(相信看到这,我应该能成功地吸引大家的注意力,帮助大家把非线性函数线性化的事情忘掉了……),如果 总是大于1,那么随着层数越深,数值的方差会越来越大,反过来如果乘积小于1,那么随着层数越深,数值的方差就会越来越小。
总是大于1,那么随着层数越深,数值的方差会越来越大,反过来如果乘积小于1,那么随着层数越深,数值的方差就会越来越小。
越来越大,就容易Hold不住导致溢出,越来越小,就容易导致数据差异小而不易产生有力的梯度。这就是深层模型的一大命门。
公式推到这里,我们不妨回头看看这个公式:

你一定会有这样一个想法(一定会有!),如果,接着我们保证每一层输入的方差都保持一致,那么数值的幅度不就可以解决了么?于是乎:

我们用均值为1,方差为上式的那个数字做初始化,不就可以解决了?
不错,从理论上讲是这个思路,不过,这只是这个思路的开始……
上回说到我们从前向的方向推导,发现了这些0均值的随机变量在计算过程中会产生方差扩散的问题,我们并且从前向的方向给出了解决的办法。既然在刚才的句子中我们反复提到了前向这两个字,那肯定是在别有用心地告诉大家——还有后向呗。
后向的计算公式其实和前向类似,忘记的可以顺便去前面的文章中回顾一下(顺便顺手点个赞啊~),这里我们还是用比较抽象的方式去表示,假设我们还是一个k层的网络,现在我们得到了第k层的梯度,那么对于第k-1层输入的梯度,有
好了,这个公式的精髓还是在意不在形,也就是说,K-1层一个数值的梯度,相当于上一层的n个参数的乘加。这个n个参数的计算方式和之前方式一样,只是表示了输出端的数据维度,在此先不去赘述了。
然后我们又到了反向传播到非线性函数的地方了,时间一长洗脑可能会失效,让我们再次催眠自己,想象非线性函数像线性函数一样飘过,飘过……
于是我们如果假设每一层的参数也服从某种均值为0,方差为某值的分布,利用这种来自东方的神秘力量,我们又可以写出一个神奇的公式:
于是乎,对于这个k层网络,我们又可以推导出一个神奇的公式:
好了,上次我说过的话不会重复再说一遍了。这次我们考虑后向操作是为了什么呢?前面我们前向传播data,我们做到了数值的稳定,现在反向传播如果不能做到同样的数值稳定,那么被diff更新过的data不再服从这种神奇的力量怎么办?要命了。
所以为了服从神奇的力量,我们又可以得到:
为了

咦,好像我们两次推导得到了同样的结果,大功告成了?如果仔细看一下这两个公式,我们就会发现两个n实际上不是同一个n。对于全连接来说,前向操作时,n表示了输入的维度,而后向操作时,n表示了输出的维度。而输出的维度也可以等于下一层的输入维度。所以两个公式实际上可以写作:


这么看上去前向后向不是很统一啊,但是大功快要告成,怎么也得再糊弄一回了,于是我们把两个公式揉合以下,就成了:

下面就是对这个方差的具体使用了。没错,前辈思来想去,决定使用均匀分布进行初始化,我们设定我们要初始化的范围是[-a,a]。熟悉均匀分布和不熟悉均匀分布的各位,都可以看一下上述的范围下,均匀分布的方差为:

将上面两个公式合并一下,就可以得到:

于是,我们的xavier初始化方法横空出世,那就是把参数初始化成![[-\sqrt{\frac{6}{n^{k+1}+n^k}},\sqrt{\frac{6}{n^{k+1}+n^k}}]](https://i-blog.csdnimg.cn/blog_migrate/814b6de252575271684bad53bdfd9b9c.png) 范围内的均匀分布。
范围内的均匀分布。
看完了这段晕晕忽忽地演绎,再看看最终的结果,和源代码,有没有一种搞了半天就弄出点这的感觉?
没错,这个初始化的公式不难,但是想这样推导出来还是让前辈们付出了巨大的心血。后人在使用这个初始化方法的时候,理所当然地使用了这些方法,但是很少去理会这些推导背后的真正含义。
虽然前面用了大量戏谑的语言来说明一些假设的不合理性,但是如果没有这些假设,我们也无法得出这样精彩而且实用的结论。其实数学模型的世界经常就是会用到一些抽象这件工具,只有把一些不太好把握的地方抽象掉,才能更容易地抓住事物的本质,找到事物的核心规律。所以在这里还是要由衷的给这个初始化算法的作者点个赞。
向更远方前进
如果熟悉Caffe源码的同学,在看到xavier的源码后,会看到下面还有一个类似结构的初始化方法——MSRAFiller。这个初始化方法来自《Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification》,不同的是,这篇文章的主要目标是基于ReLU的初始化算法,实际上它的推导过程和我们看过的xavier的方法类似,只是在一些细节处有所不同。如果你理解了xavier的演绎思想,不妨去看看这篇文章的推导过程,相信你会很轻松地理解这一路研究初始化算法的思路。总之,能够出现在应用中的算法都是经过一定实践检验的算法,已经被人证明了它在理论和实践上的可行性,是完全值得去深入了解的。
除了这两篇文章,还有很多大牛写了关于初始化的文章,以它们的角度讲述了它们心中初始化的样子。后面有时间我们还会继续去看这些文章,不过我们要暂时停下脚步了,因为还有在其他方向努力的前辈们要急着登场了,它们又会给我们带来一个全新的角度去理解CNN……
为了使得网络中信息更好的流动,每一层输出的方差应该尽量相等。
基于这个目标,现在我们就去推导一下:每一层的权重应该满足哪种条件。
文章先假设的是线性激活函数,而且满足0点处导数为1,即
现在我们先来分析一层卷积:
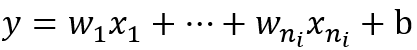
其中ni表示输入个数。
根据概率统计知识我们有下面的方差公式:
特别的,当我们假设输入和权重都是0均值时(目前有了BN之后,这一点也较容易满足),上式可以简化为:
进一步假设输入x和权重w独立同分布,则有:
于是,为了保证输入与输出方差一致,则应该有:
对于一个多层的网络,某一层的方差可以用累积的形式表达:
特别的,反向传播计算梯度时同样具有类似的形式:
综上,为了保证前向传播和反向传播时每一层的方差一致,应满足:
但是,实际当中输入与输出的个数往往不相等,于是为了均衡考量,最终我们的权重方差应满足:
———————————————————————————————————————
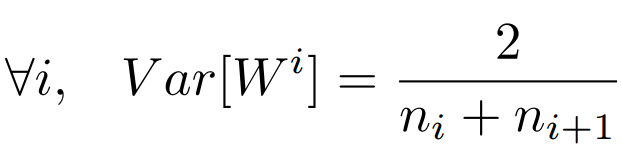
———————————————————————————————————————
学过概率统计的都知道 [a,b] 间的均匀分布的方差为:
因此,Xavier初始化的实现就是下面的均匀分布:
——————————————————————————————————————————
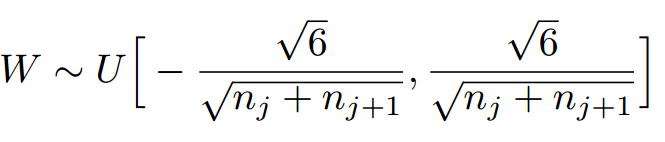
———————————————————————————————————————————
下面,我们来看一下caffe中具体是怎样实现的,代码位于include/caffe/filler.hpp文件中。
template <typename Dtype>
class XavierFiller : public Filler<Dtype> {
public:
explicit XavierFiller(const FillerParameter& param)
: Filler<Dtype>(param) {}
virtual void Fill(Blob<Dtype>* blob) {
CHECK(blob->count());
int fan_in = blob->count() / blob->num();
int fan_out = blob->count() / blob->channels();
Dtype n = fan_in; // default to fan_in
if (this->filler_param_.variance_norm() ==
FillerParameter_VarianceNorm_AVERAGE) {
n = (fan_in + fan_out) / Dtype(2);
} else if (this->filler_param_.variance_norm() ==
FillerParameter_VarianceNorm_FAN_OUT) {
n = fan_out;
}
Dtype scale = sqrt(Dtype(3) / n);
caffe_rng_uniform<Dtype>(blob->count(), -scale, scale,
blob->mutable_cpu_data());
CHECK_EQ(this->filler_param_.sparse(), -1)
<< "Sparsity not supported by this Filler.";
}
};由上面可以看出,caffe的Xavier实现有三种选择
(1) 默认情况,方差只考虑输入个数:
(2) FillerParameter_VarianceNorm_FAN_OUT,方差只考虑输出个数:
(3) FillerParameter_VarianceNorm_AVERAGE,方差同时考虑输入和输出个数:
之所以默认只考虑输入,我个人觉得是因为前向信息的传播更重要一些
torch中,需要额外下载torch工具包,里面包换weight_init.lua文件中有实现。








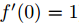
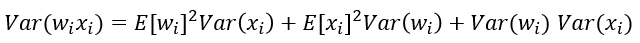
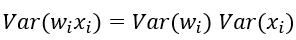
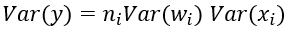
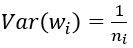
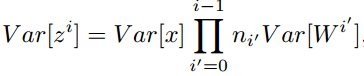
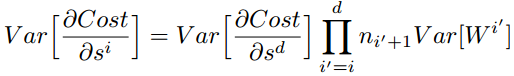
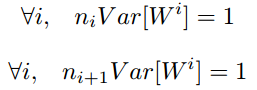
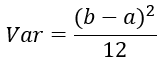
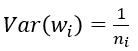
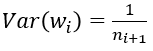
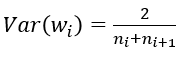














 885
885

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








