机器学习之支持向量机

最新推荐文章于 2024-06-11 02:53:31 发布

AstronomyFirst

最新推荐文章于 2024-06-11 02:53:31 发布

阅读量828

点赞数 20

文章标签：机器学习支持向量机人工智能

本文链接：https://blog.csdn.net/AstronomyFirst/article/details/139297523

版权

一.支持向量机

1.什么是支持向量机

支持向量机（Support Vector Machine，简称SVM）是机器学习中的一种重要算法，尤其在分类和回归分析领域具有广泛应用。它的核心思想是在特征空间中找到一个最优的超平面，以将不同类别的样本分开。

2.超平面

将数据集分为两个或多个类别，然后构建一个最优超平面，这个超平面也被称为“判定边界”或“分隔超平面”。这个超平面的目标是最大化两个类别之间的间隔，也就是找到一个能够最大程度将两个类别分开的决策边界。

3.支持向量

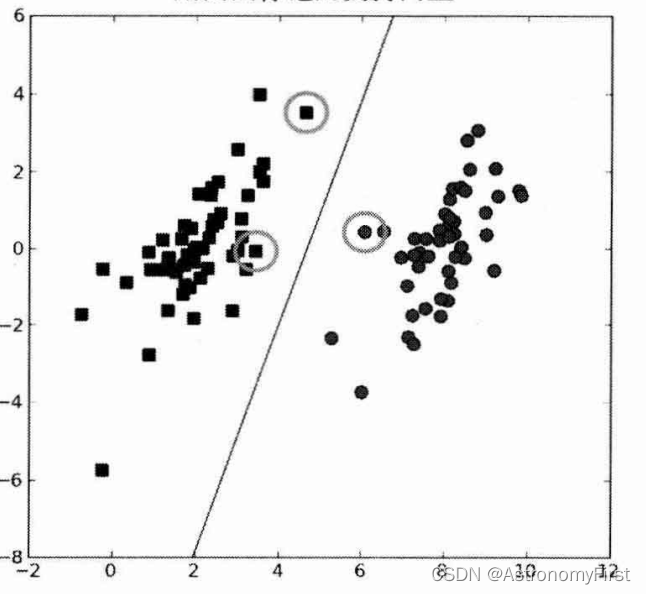
支持向量是离超平面最近的那些样本点，它们决定了超平面的位置和方向。在SVM中，只有支持向量对分类决策有影响，而其他远离超平面的样本点则对分类决策没有影响。（下图中被圆圈标记的数据点，即为支持向量；图中的那条直线即为超平面）

4.核函数

核函数是将原始输入空间映射到新的特征空间的一种函数，使得原本线性不可分的样本在新的特征空间中可能变得线性可分。

在SVM中，当数据在原始空间中不是线性可分时，我们希望通过一个映射函数将数据映射到一个高维空间中，使得数据在高维空间中变得线性可分。然而，直接寻找这样的映射函数是困难的，因此我们使用核函数来间接地实现这一目的。

5.优缺点

优点：1>泛化错误率低，计算开销不大，结果容易解释

2>高维数据的处理能力：SVM可以有效地处理高维数据，因为在高维空间中，数据点更有可能变得线性可分

3>泛化能力强 4>适用于小样本学习

缺点：1>对参数调节和核函数的选择敏感，原始分类器不加修改仅适用于处理二分类问题

2>对于大规模的数据集的训练时间较长

二.详细解读支持向量机

1.超平面解读

1>如果数据分布在一条数轴上，我们可以尝试找到一个点来把两类样本分开；如果数据分布在一个平面上，我们可以尝试这样一条直线，把两类样本分开；如果数据分布在三维空间，我们也可以找到这样一个平面来分类；所以当维度等于n的时候，我们就可以用n-1维度的超平面来实现分类。超平面也就是分类的决策边界。（下图中的黄色标记即为超平面）

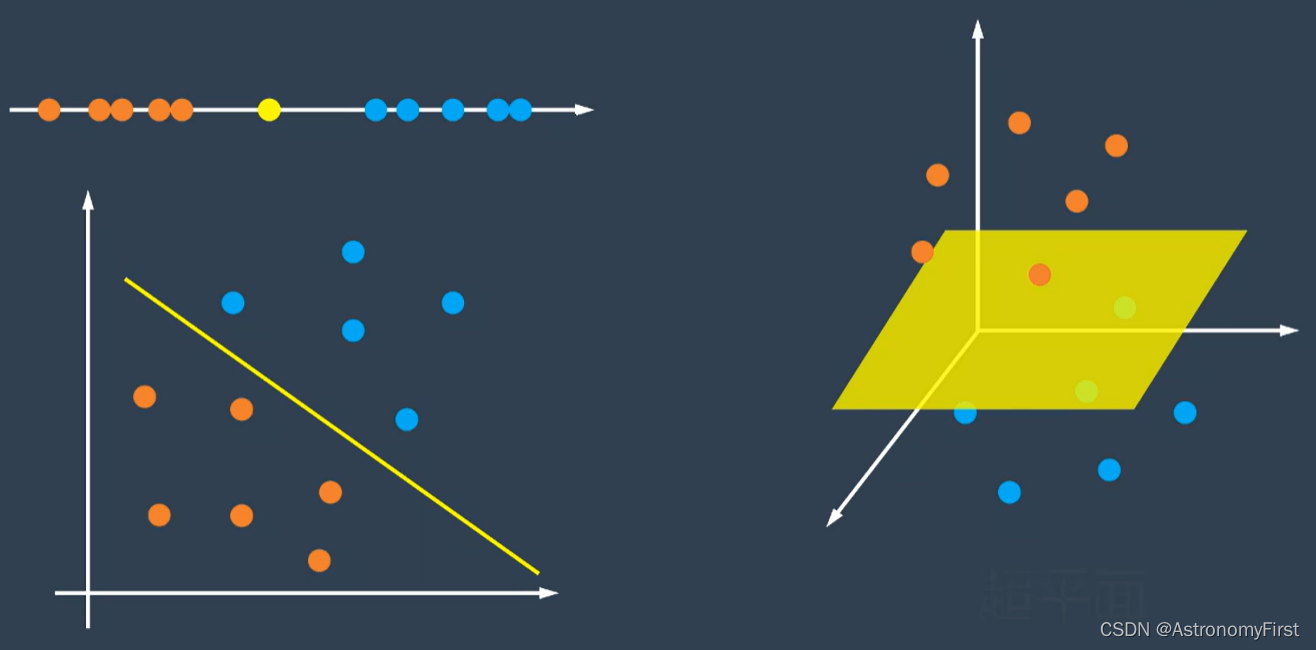
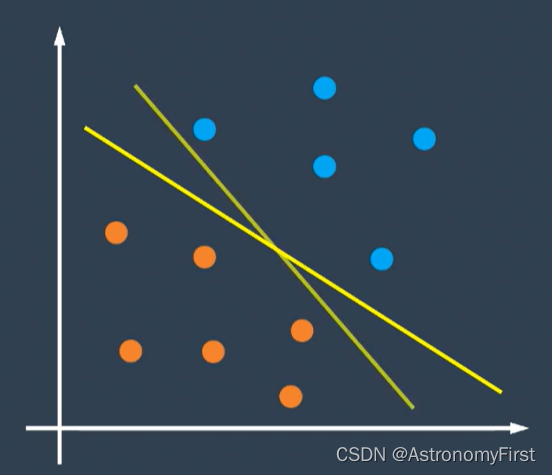
2>我们现在讨论二维的情况，对于下面的数据点，我们可以画这两条直线来实现对样本的分类，那么究竟哪个超平面是最好的呢？本次实验的支持向量机就可以实现找到最好的超平面。即找到这样一条直线，让直线两边的点与它的距离是最大的。

2.函数间隔

1>假设平面上的任意一点的横坐标是x1，纵坐标是x2，类别等于1（图中蓝色数据点）或者-1（图中橙色数据点）。超平面的方程为w1x1+w2x2+b=0。

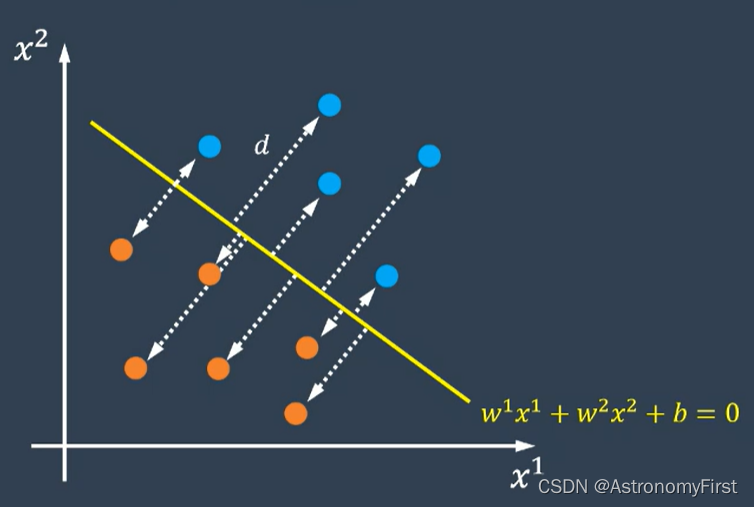
2>平面上一点到直线的距离这样求的：

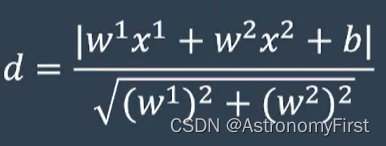
若分子里面的绝对值是正数，说明类别等于1（因为类别为1的数据点是在超平面的上方），若分子里面的绝对值是负数，说明类别等于-1；因此我们可以拿掉绝对值，用一个y来代替（y=1表示蓝色数据点，y=-1表示橙色数据点），结果如下：

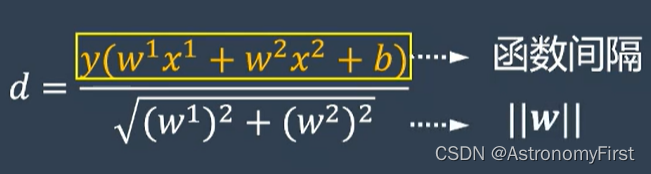
3>分子的这种形式被称为函数间隔，分母为w的范数，若用伽马来代表函数间隔，则d可表示为：

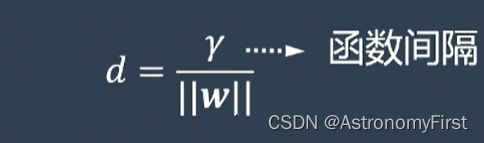
4>若要找到距离所有的点间隔都是最大的直线，我们首先要找到间隔最小的那些点（即支持向量）

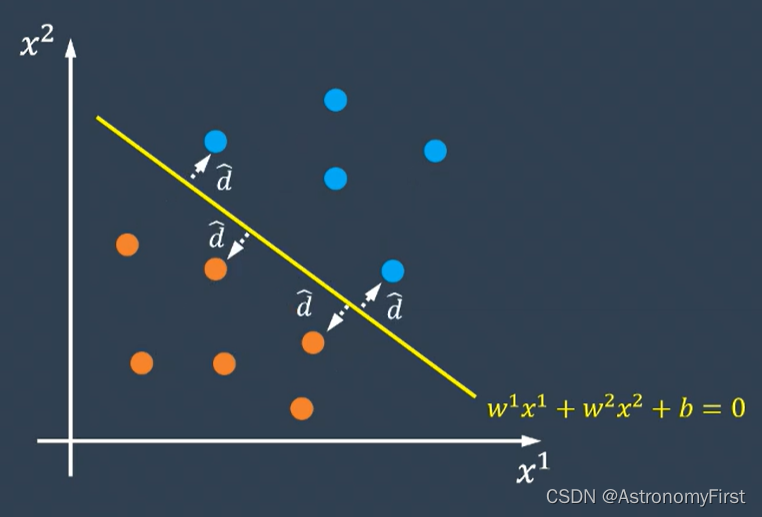
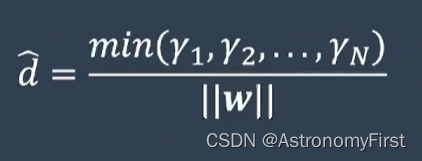
5>再让这些间隔最小的点，让最终的直线距离它们最大，即：

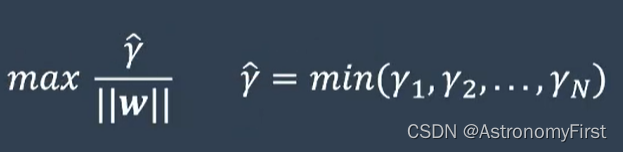
也就是：

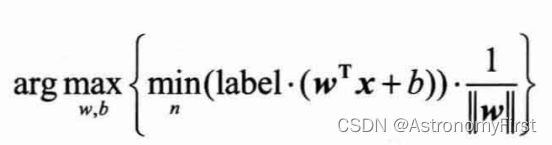
6>由于直接求解上类问题十分困难，所以令支持向量的函数间隔为1，这是基于间隔最大化原理和对偶问题的求解简化，有助于我们找到一个具有强泛化能力的分类超平面。因此问题可以转化为如下的形式：

等价于：

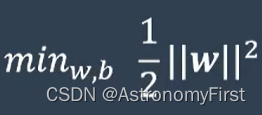
3.求解w，b

1>以上的最优化问题，根据拉格朗日乘子法，可以构建他的对偶问题为：

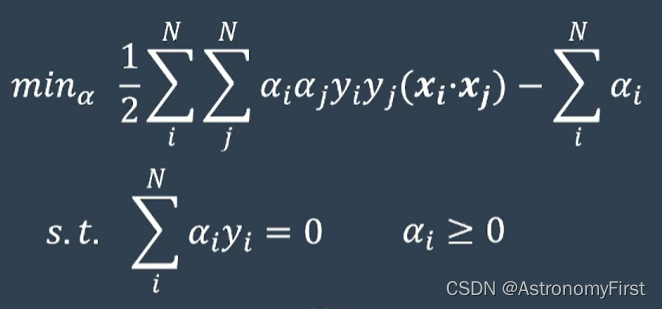
2>通过这个对偶问题，就可以得到一系列的阿尔法值，w和b就可以通过如下的公式计算出来（该类问题是线性可分的问题，因此该方法也称为硬间隔支持向量机）：

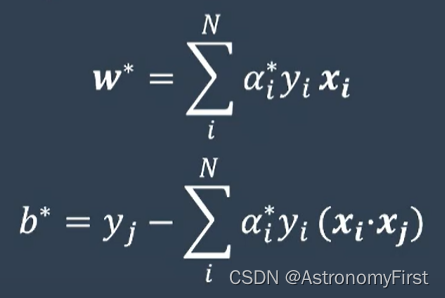
三.支持向量机的类别

1.硬间隔支持向量机

在数据完全线性可分的情况下，通过最大化分类间隔（margin）来找到最优的决策边界。构建的对偶问题以及w和b的求解公式如下：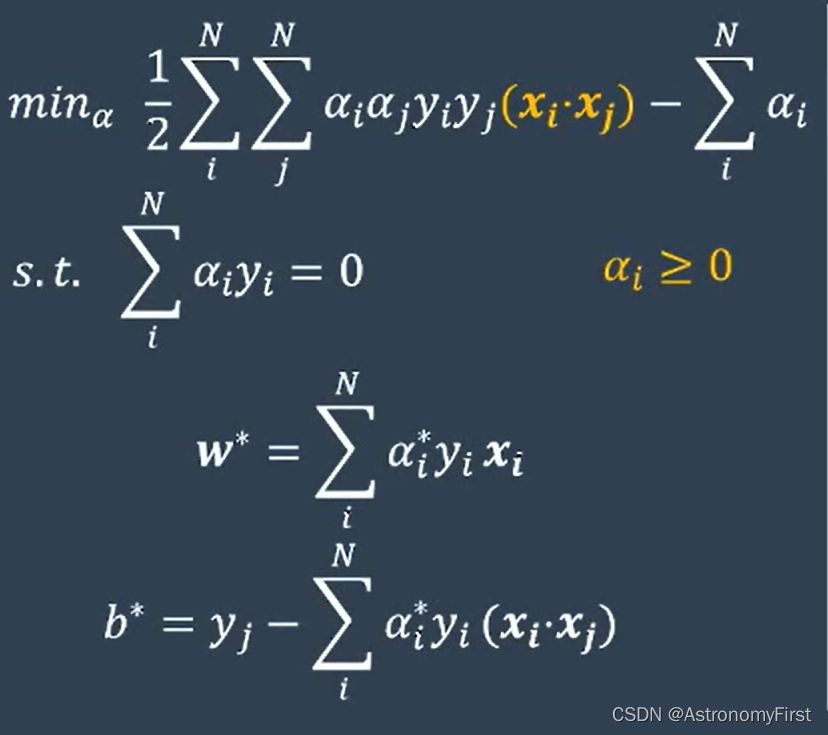

2.软间隔支持向量机

1>由于如下图中两个错开点的存在，不可能找到一条直线把两类数据完全分开，但是大多数的点是可以的，因此这些样本是弱线性可分的，但我们仍然可以通过支持向量机找到一个次优解。

2>但需要有错误的点处于这个间隔之内，因此对于任何一个样本函数间隔不再>=1，而是放宽了距离限制，增加了一个松弛变量ξ，如下：

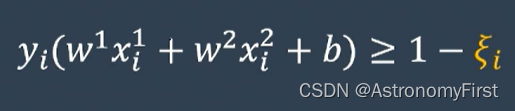
3>因此对于优化问题需要增加一个惩罚项，优化问题转化如下：

4>对应的对偶问题以及w和b的求解公式如下（可以注意到，只是阿尔法的取值范围改变）（该方法用于处理线性不可分的数据，也被称为软间隔支持向量机）：

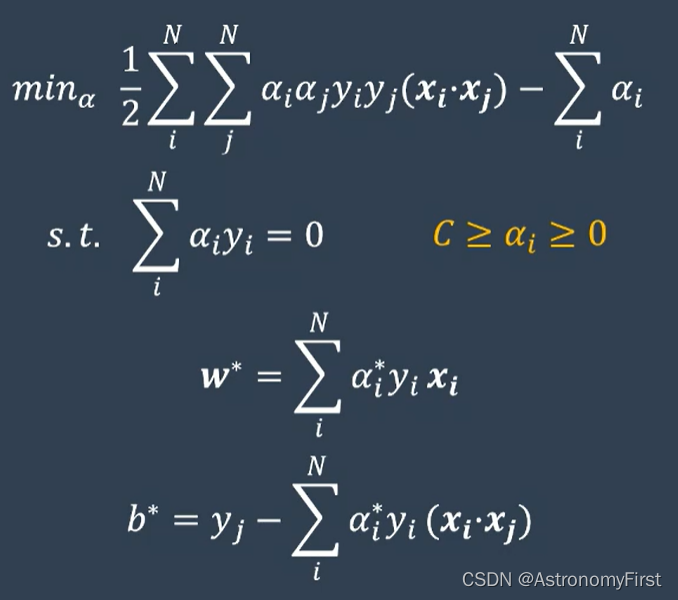
3.非线性支持向量机

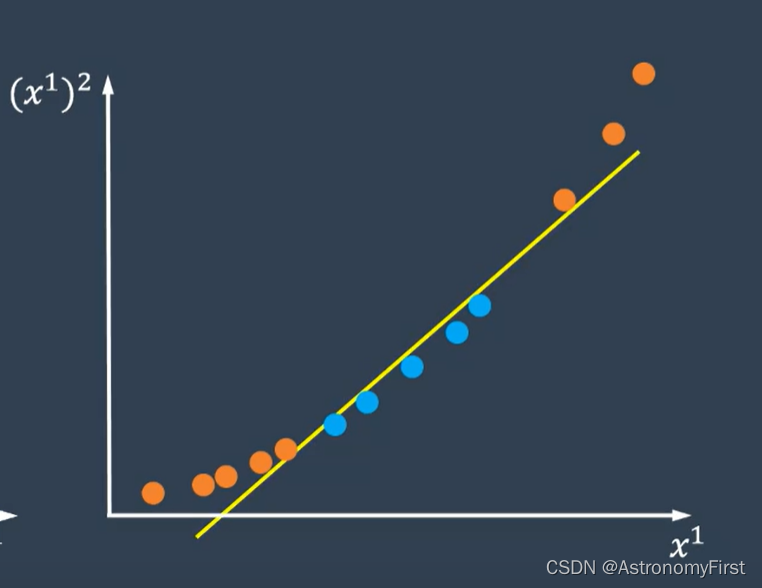
1.在这条直线上，无论我们用什么方法，都不可能将两类数据完全分开。

2.因此我们换一个思路，将数据增加一个维度，使用x1的平方来构建第二个维度，这样我们又可以用一条直线将两类数据分开了。

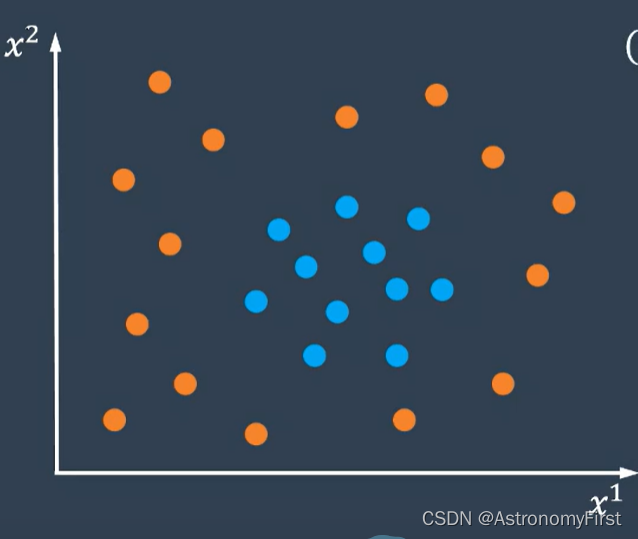
3.假如又有一些数据，它们的分布如下（类似于椭圆分布）：

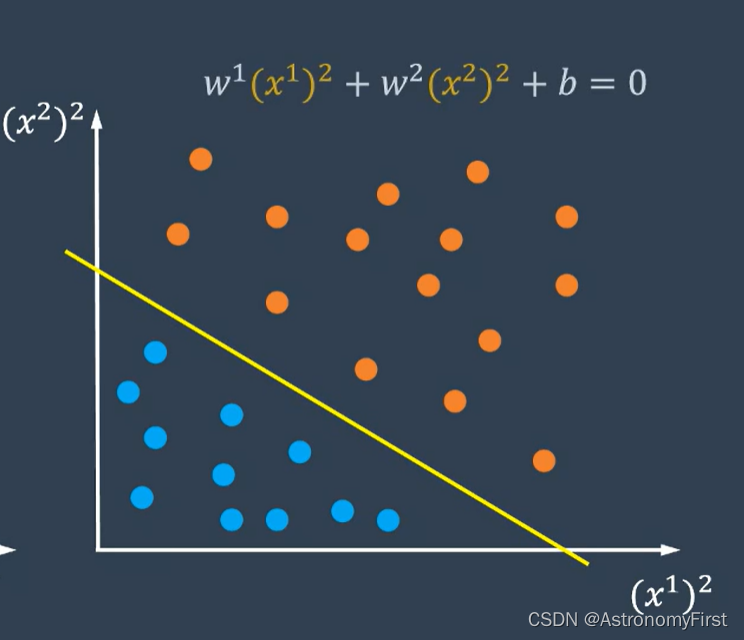
4.我们可以利用x1的平方和x2的平方为数轴，将数据点重新映射到平面上，这样将线性不可分的问题又转化为线性可分的问题了。这种通过升维或者空间映射的方法也被称为非线性支持向量机。

5>我们利用一个phi函数把x1映射为x1的平方，x2映射为x2的平方。并定义另一个函数k，代表变换之后两个样本点积的结果，该函数也被称为核函数。这样非线性分类问题的对偶问题以及w和b的求解公式如下：

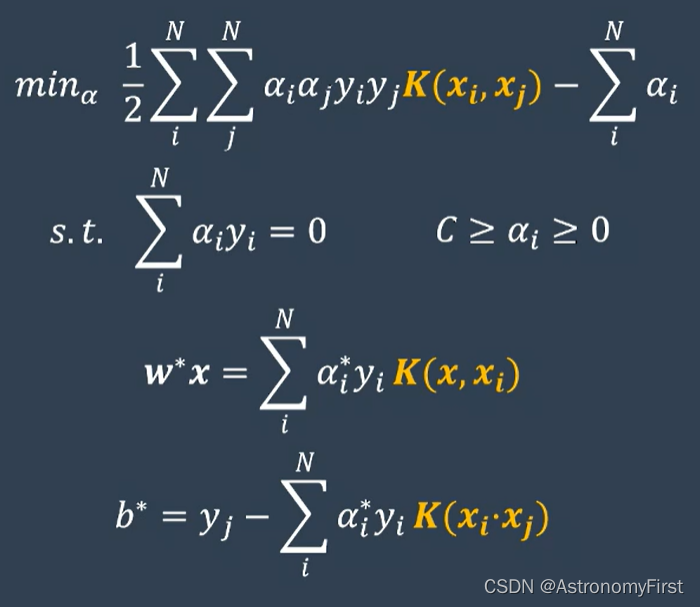
四.支持向量机解决数据点分类问题

1.代码实现

1>首先导入所需要的包：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

2>使用sklearn.datasets模块中的make_blobs函数来生成模拟数据集：

X, y = datasets.make_blobs(n_samples=100, centers=2, random_state=6)

(1)代码解释：函数中的三个参数分别代表：

n_samples:生成的数据集将包含100个样本

centers:数据集将被分为两个类别，这意味着生成的数据将有两个中心点，围绕这两个中心点随机生成样本

random_state:随机数生成器的种子值。设置这个值可以确保每次调用make_blobs时生成的数据都是相同的

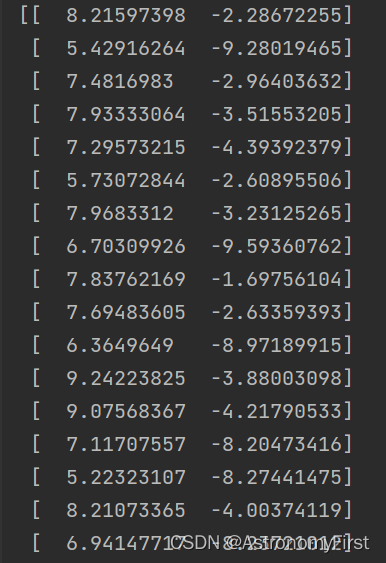
(2)X,y的运行结果（部分X）：

3>构建Linear类：

class LinearSVM:#定义LinearSVM类
    #LinearSVM属性初始化，当创建一个LinearSVM类对象时，会自动调用该方法，对该类对象的各个属性进行初始化
    def __init__(self, learning_rate=0.001, lambda_param=0.1, n_iters=1000):
        self.learning_rate = learning_rate  #学习率
        self.lambda_param = lambda_param    #正则化参数，控制模型对错误分类的容忍度与决策边界的简单性的权衡
        self.n_iters = n_iters              #迭代次数
        self.w = None    #权重向量
        self.b = None    #偏置值

    def fit(self, X, y):
        n_samples, n_features = X.shape   #获取样本点数量和特征值数量
        y_ = np.where(y<=0, -1 , 1)       #对于y中的数据，当标签值<=0时，更改为-1，否则更改为1
        self.w = np.zeros(n_features)     #w初始化为长度n_features的零向量
        self.b = 0   #b初始化为0
        for _ in range(self.n_iters):     #进行次数为n_iters的迭代来训练模型
            for idx, x_i in enumerate(X): #enumerate内置函数，用于将可遍历的对象组合为一个索引序列
                condition = y_[idx] * (np.dot(x_i, self.w) - self.b) >=1 #计算函数间隔，并检查是否>=1
                if condition:
                    #条件为真，进行权重衰减
                    self.w -= self.learning_rate * (2 * self.lambda_param * self.w)
                else:
                    #条件为假，利用正则化和梯度下降更新w和b
                    self.w -= self.learning_rate * (2 * self.lambda_param * self.w - np.dot(x_i, y_[idx]))
                    self.b -= self.learning_rate * y_[idx]

    def predict(self, X):
        linear_output = np.dot(X, self.w) - self.b
        return np.sign(linear_output)

（1）代码解释：

__init__函数：该函数声明了LinearSVM类所具有的相关的属性，并且在该类的实例化对象被创建的时候，会自动调用该函数，为该实例化对象附上相应的初值

predict函数：该函数实现对输入的样本点X的类别进行预测，返回该样本点的预测结果

fit函数：通过一定的迭代次数来训练模型，从而得到相应的w和b的值。当对应的样本点的函数间隔>=1的时候，不直接更新权重w，而是通过权重衰减来稍微减小权重的大小，避免权重过大而导致过拟合；当样本点的函数间隔小于1的时候，则通过正则化和梯度下降来更新权值w和偏置值b

4>可视化函数：

def plot_hyperplane(X, y, w, b):
    plt.scatter(X[:, 0],X[:, 1], marker='o', c=y, s=100, edgecolors='k', cmap='winter') #绘制数据点
    ax = plt.gca()        #获取轴对象并获取该轴的x和y的界限
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()
    xx = np.linspace(xlim[0], xlim[1], 30) #创建网络
    yy = np.linspace(ylim[0], ylim[1], 30)
    YY, XX = np.meshgrid(yy, xx)
    xy = np.vstack([XX.ravel(), YY.ravel()]).T  #评估决策函数
    Z = (np.dot(xy, w) - b).reshape(XX.shape)
    ax.contour(XX, YY, Z, color='k', levels=[-1, 0 ,1], alpha=0.5, linestyles=['--', '-', '--']) #绘制决策边界和正负区域
    plt.show()

（1）代码解释：

plt.scatter：这个函数是matplotlib库中绘制散点图的函数。X[:,0]表示选择X的第一列作为散点图每个点的x坐标；X[:,1]表示选择X的第二列作为散点图的y坐标；c=y表示点的颜色由y数组中的值决定（y数组中的每个值都会映射到cmap参数指定的颜色映射中的一个颜色）；s=100指定了每个点的大小为100；edgecolors='k'表示点的边缘的颜色为黑色；cmap='winter'意味着y数组中的值将被映射到'winter'颜色映射中的颜色

ax=plt.gca()：获取坐标轴对象

xlim=ax.get_xlim()：用于获取当前坐标轴x的限制，返回值是包含两个元素的元组，第一个元素是x轴的最小值，第二个元素是x轴的最大值

ylim=ax.get_ylim()：获取y轴的限制，返回值同样是一个包含两个元素的元组，第一个元素是y轴的最小值，第二个元素是y轴的最大值

xx(yy)=np.linspace(xlim[0](ylim[0]),xlim[1](ylim[1]),30)：用于生成一维数组，数组中的元素是等间隔的。该数组包含30个等间隔的值，这些值从xlim[0](ylim[0])开始到xlim[1](ylim[0])结束

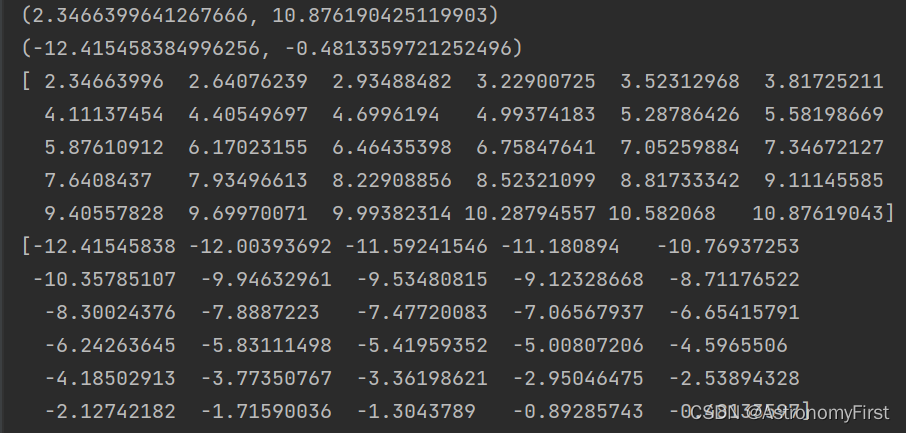
xlim，ylim，xx，yy的运行结果如下：

YY,XX=np.meshgrid(yy,xx)：返回两个二维矩阵，第一个矩阵对应于 y 坐标（即行），第二个矩阵对应于 x 坐标（即列）。YY矩阵中的每个元素表示网格中对应点的 y 坐标，如果YY有m行n列，那么它就有 m*n 个元素，每个元素对应于网格中的一个点的 y 坐标。XX矩阵同理。

xy = np.vstack([XX.ravel(), YY.ravel()：

ravel() 函数将 XX（一个二维数组）转换为一个一维数组，包含 XX 中的所有元素

vstack() 函数将两个一维数组（XX.ravel() 和 YY.ravel()）垂直堆叠成一个二维数组。结果是一个 (2, N) 形状的二维数组，其中 N 是 XX 和 YY 中的元素数量

T 属性（或方法，取决于你如何看它）是 NumPy 数组的一个转置操作。它交换数组的轴，将 (2, N) 形状的数组转换为 (N, 2) 形状的数组

最终，xy 是一个 (N, 2) 形状的二维数组，其中 N 是网格点的数量，每一行都是一个 (x, y) 坐标对

Z = (np.dot(xy, w) - b).reshape(XX.shape)：计算了一个线性函数在给定坐标网格上的值，并将结果重新整形为与坐标网格相同的形状

ax.contour(XX, YY, Z, color='k', levels=[-1, 0 ,1], alpha=0.5, linestyles=['--', '-', '--'])：绘制等高线图。levels=[-1, 0, 1]：这指定了要绘制哪些等高线级别；alpha=0.5：这指定了等高线的透明度；linestyles=['--', '-', '--']：这指定了每个等高线的线型。

5>实例化对象，构建超平面，并通过可视化显示：

    X, y = datasets.make_blobs(n_samples=100, centers=2, random_state=6)
    svm = LinearSVM()
    svm.fit(X, y)
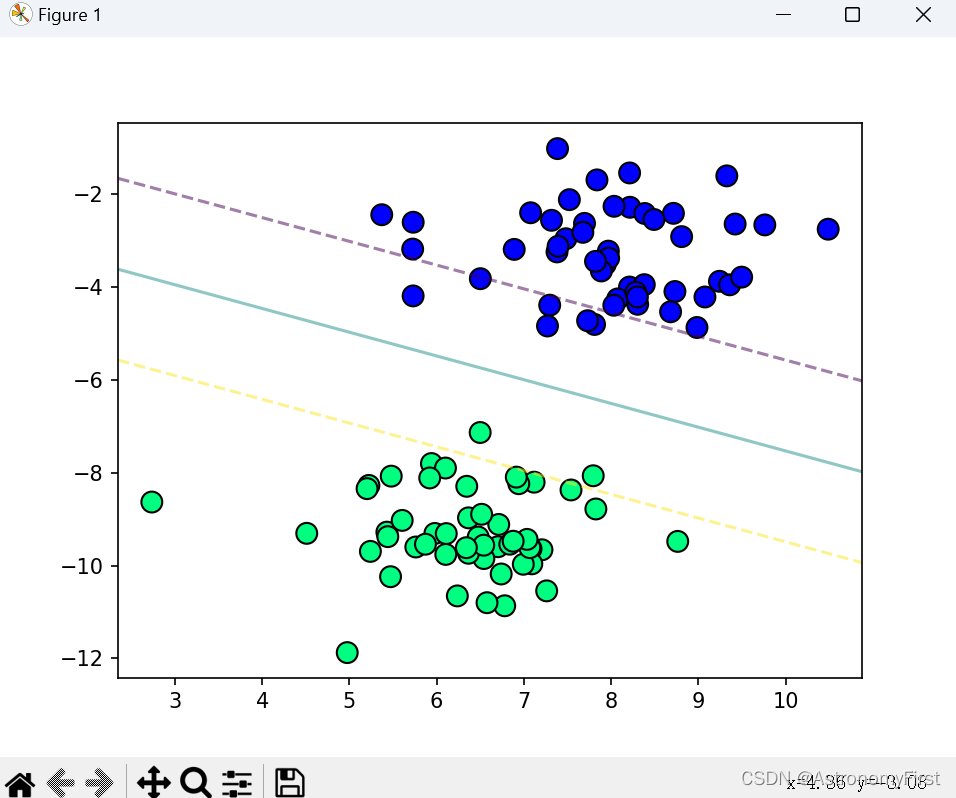
    plot_hyperplane(X, y, svm.w, svm.b)

初始化函数中的lamda_param更改为0.1可得到如下的结果：

将初始化函数中的lamda_param更改为0.001可得到如下的结果：

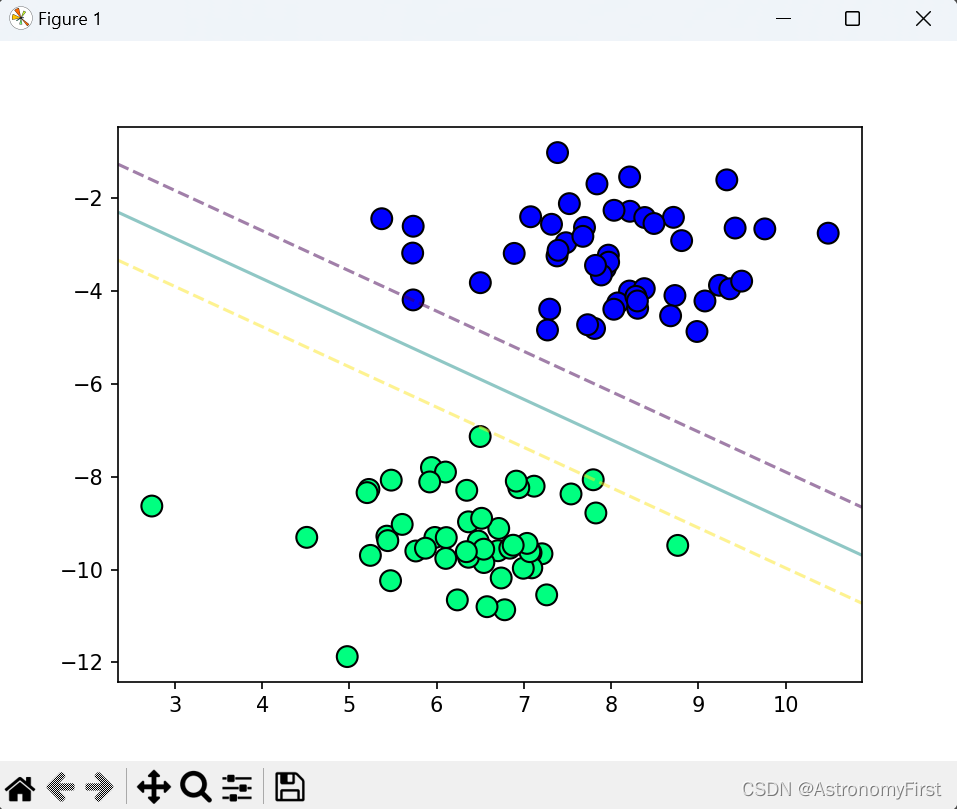
2.结果分析

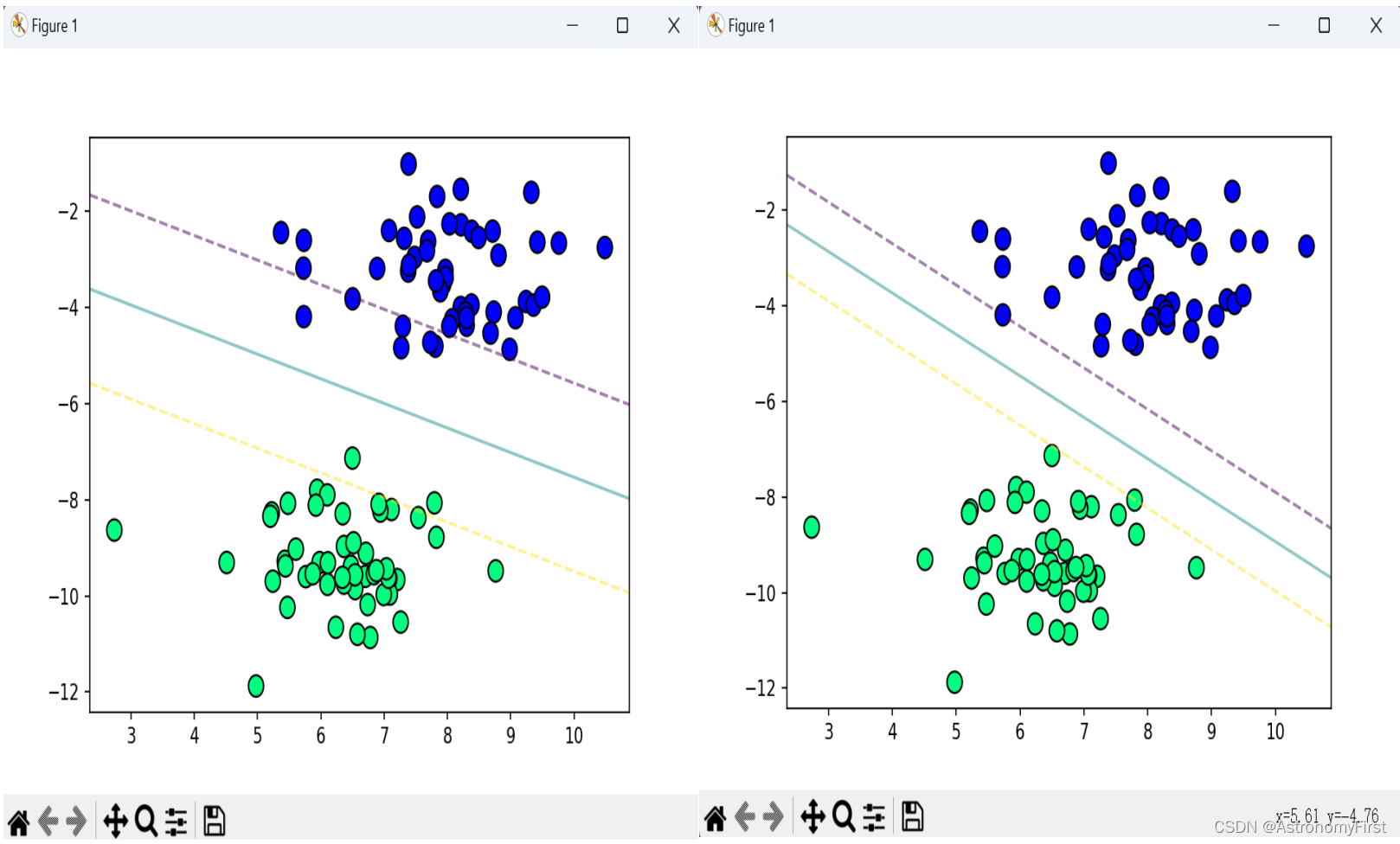
由上图的运行结果可知，左侧明显有大量的数据点是位于''间隔''之内的。

在硬间隔支持向量机的理想情况下，是不允许有任何数据点落在决策边界与决策超平面之间的。因此，左侧的模型所训练出来的结果是不当的。

而造成这样的结果是参数lamda_param设置不当，导致模型对噪声和异常值过于敏感，从而将一些本应在间隔之外的数据点错误地分类到间隔之内。

将参数lamda_param修改为0.001后运行结果如右图。所有的数据点都位于''间隔''之外，完全被超平面所分隔，为正确的硬间隔支持向量机划分不同类别数据的结果。

五.总结

通过本次实验，我明白了支持向量机是机器学习中的一种强大算法，特别适用于处理二维线性可分类的数据点。其核心思想是通过寻找一个超平面来划分不同类别的数据点，使得该超平面到两个类别中最近数据点的距离最大化，这些最近的数据点被称为支持向量。

同时我也明白了SVM具有高效、稳健和准确的特性，尤其在小样本、高维数据和非线性问题中表现出色。在二维空间中，SVM能够将数据点划分为两个明确的区域，每个区域代表一个类别。通过调整超平面的参数，SVM可以适应不同的数据分布，并处理噪声和异常值。此外，SVM还可以结合核技巧来处理非线性分类问题，将原始数据映射到更高维的特征空间，使得数据在该空间中线性可分。

总之，通过本次实验我明白了支持向量机在处理二维线性可分类的数据点方面表现出色，其高效、稳健和准确的特性使其成为机器学习中的一种重要算法。