目录
一.主成分分析(PCA)
1.概念
主成分分析(Principal Component Analysis,简称PCA)是一种在机器学习、数据分析和统计学中广泛使用的技术,主要用于数据的降维和特征提取。其核心思想是将原始的高维数据投影到一个低维空间,同时尽可能地保留数据中的方差信息,即数据的主要特征。
2.什么是降维
想象这样一种场景:我们正通过电视而非现场观看体育比赛,在电视的纯平显示器上有一个球。显示器大概包含了100万像素,而球则可能是由较少的像素组成的,比如说一千个像素。在大部分体育比赛中,我们关注的是给定时刻球的位置。人的大脑要想了解比赛的进展,就需要了解球在运动场中的位置。对于人来说,这一切显得十分自然,甚至都不需要做任何思考。在这个场景当中,人们实时地将显示器上的百万像素转换成为了一个三维图像,该图像就给出了运动场上球的位置。在这个过程中,人们已经将数据从一百万维降至了三维。

在上述体育比赛的例子中,人们面对的原本是百万像素的数据,但是只有球的三维位置才最重要,这就被称为降维。
3.数据简化的好处
1>使得数据集更易使用 2>降低很多算法的计算开销
3>去除噪声 4>使得结果易懂
4.实现步骤
1>数据标准化:将原始数据减去均值并除以标准差,以消除量纲和尺度的影响
2>计算协方差矩阵
3>计算协方差矩阵的特征值和特征向量
4>选择前k个特征向量(即主成分),并将原始数据投影到这k个特征向量上,得到降维后的数据
5.优缺点
优点:(1)降低数据的复杂性,识别最重要的多个特征
(2)可以用于数据的可视化(将二维或三维数据投影到二维平面上进行可视化)
缺点:(1)不一定需要,且可能损失有用信息
(2)对数据的尺度敏感,因此在进行PCA之前通常需要对数据进行标准化处理
二.详细介绍
1.PC1和PC2
1>首先有如下的表格信息,有六个老鼠样本,每个老鼠样本含有两个基因,基因1和基因2,表中的数据则代表对应的老鼠样本中基因1和基因2所占的数值大小
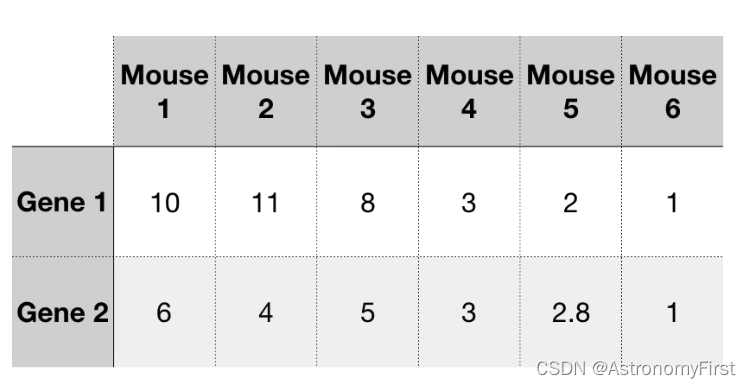
2>如果将图中的数据以基因1为x轴,基因2为y轴绘制图像,则对应的图像结果如下:
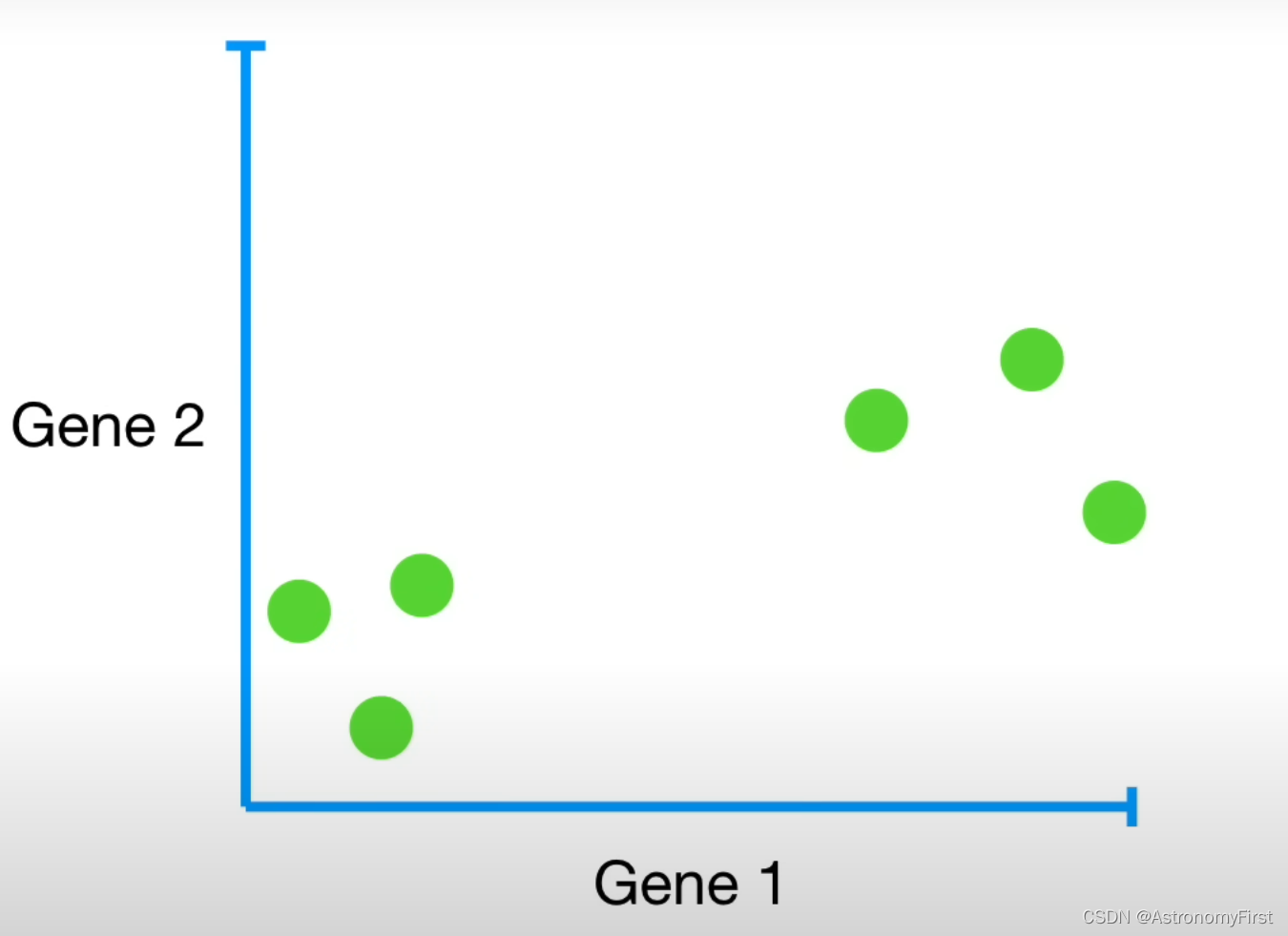
3>紧接着,我们通过计算基因1和基因2数据和的平均值来计算出数据的中心;这时,为了更好地理解什么是第一个主成分(PC1)和第二个主成分(PC2);我们将专注于图中发生的情况,不再去分析原始的数据。
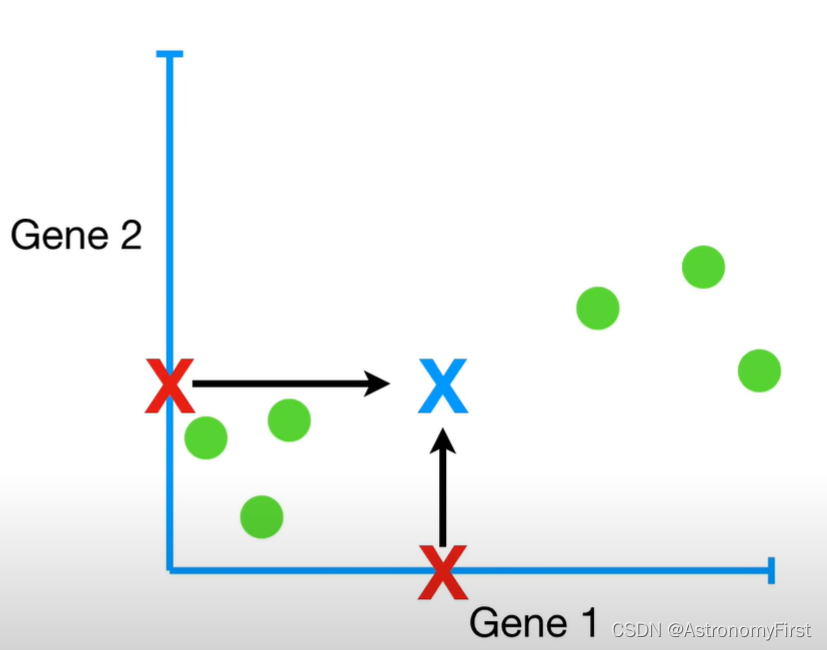
4>现在我们移动数据,使中心位于图形的原点(0,0)之上。这里注意,移动数据并不会改变数据点彼此之间的相对位置。

5>这时,我们可以绘制一条穿过原点的随机线,然后旋转线,直到它尽可能地去拟合这些数据,同时,保证这条直线始终是穿过原点的,最终,我们可以找到这样一条的直线,它能最好地拟合这些数据
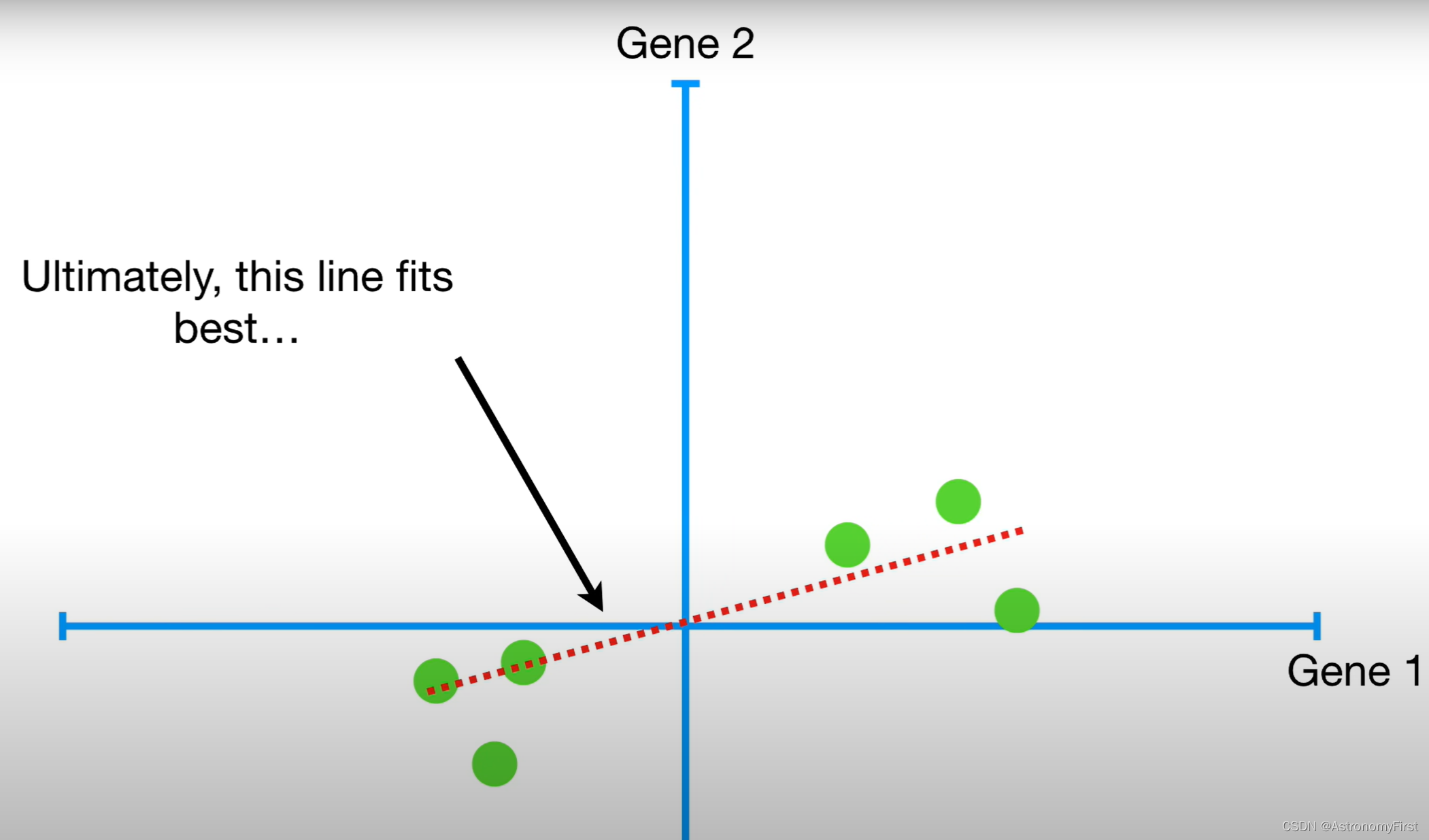
6>但是如何找到这样的一条直线来最好地拟合这些数据呢,这里我们就要谈谈PCA是如何判定拟合度的高低;因此,让我们回到最开始经过原点的一条随机线。为了量化这条线拟合数据的程度,PCA将数据投影到这条直线上。然后可以通过测量各个数据到直线的距离,并最小化所有数据点到直线的距离和,而使距离和最小的那条直线就是我们所要找的最佳的拟合直线。或者通过最大化各个数据的投影点到原点的距离和,来找到相应的最佳的拟合的直线。
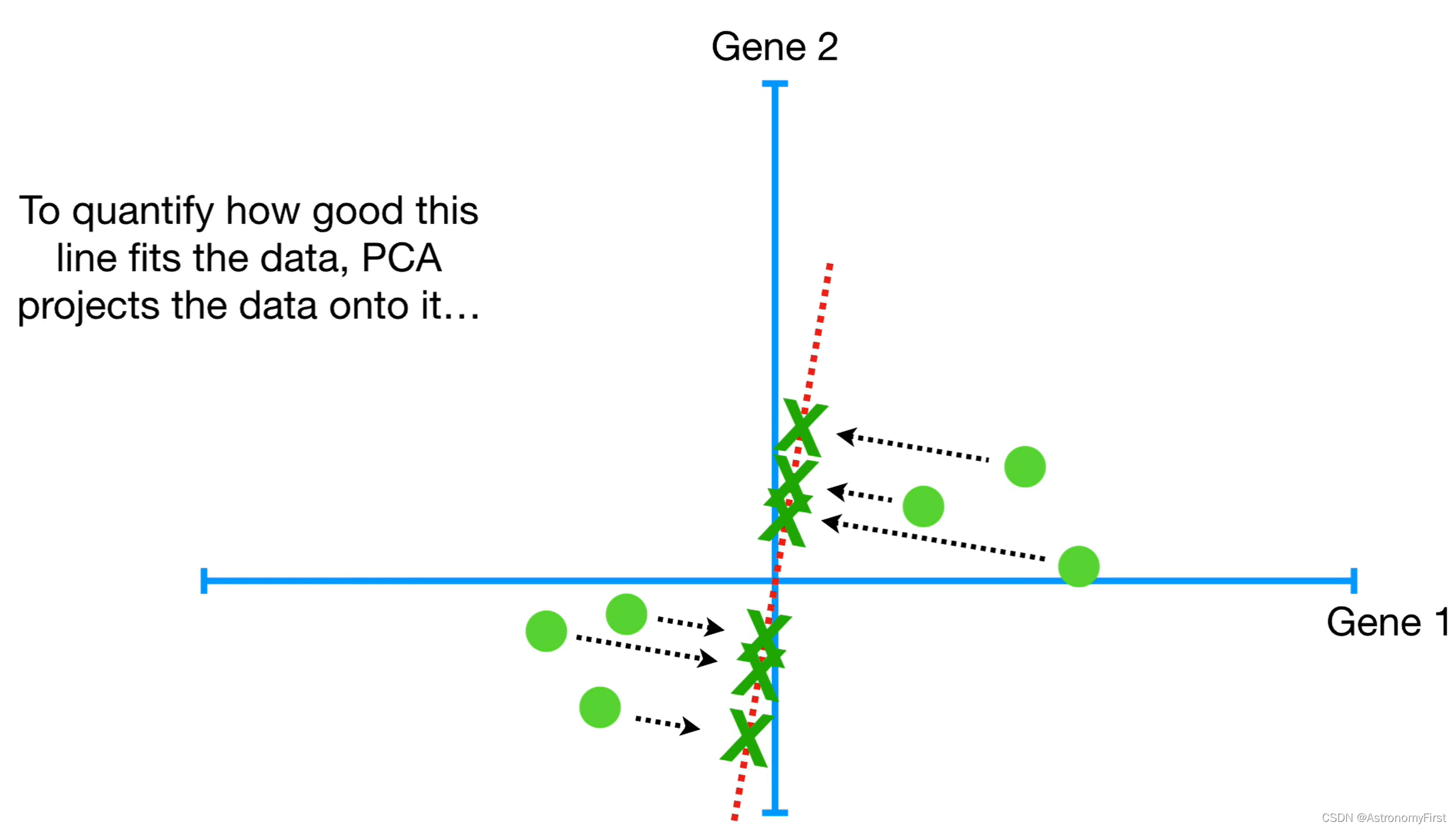
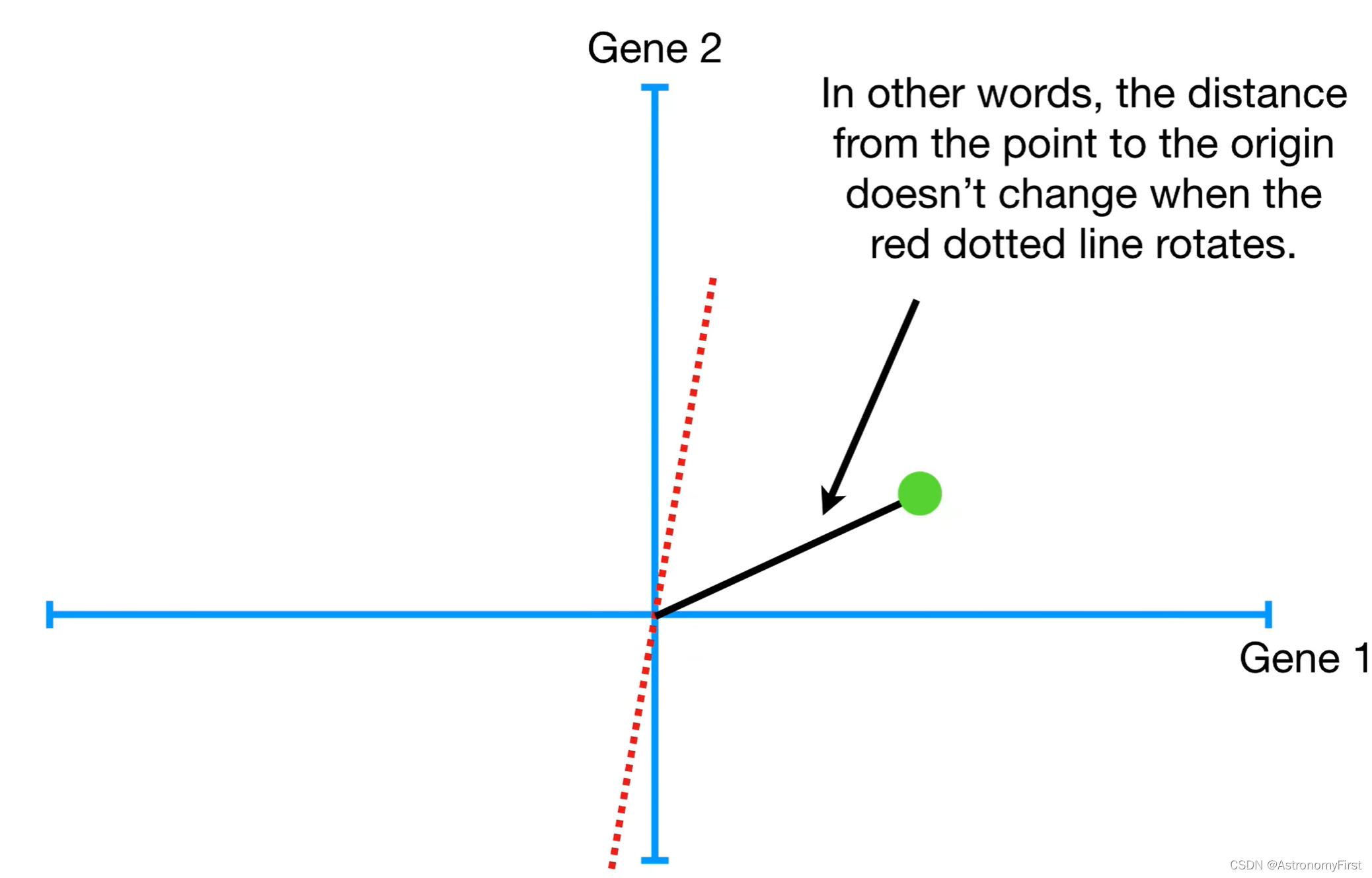
7> 如果你觉得简单晦涩的文字难以理解上面两种确定最佳拟合直线的方法,那我们接下来继续往下看,用数学的方式来解释。现在,我们随机考虑一条过原点的直线,并只考虑一个数据点。因为数据点是固定的,因此这个数据点到原点的距离也是确定的。也就是说这条随机的直线,无论怎么旋转,这个数据点到原点的距离始终是不变的。
8>此时,我们将数据点投影到该直线上,根据勾股定理可以得到,a的平方+b的平方=c的平方。因为a的值是固定的,所以b和c是逆相关的。所以按照上面的两种方式,我们可以直接最小化各个数据点的b的和来得到最佳拟合直线,也可以通过最大化各个数据点的投影点到原点的距离和(即c)来间接地得到各个数据点到直线的距离c的和的最小值。
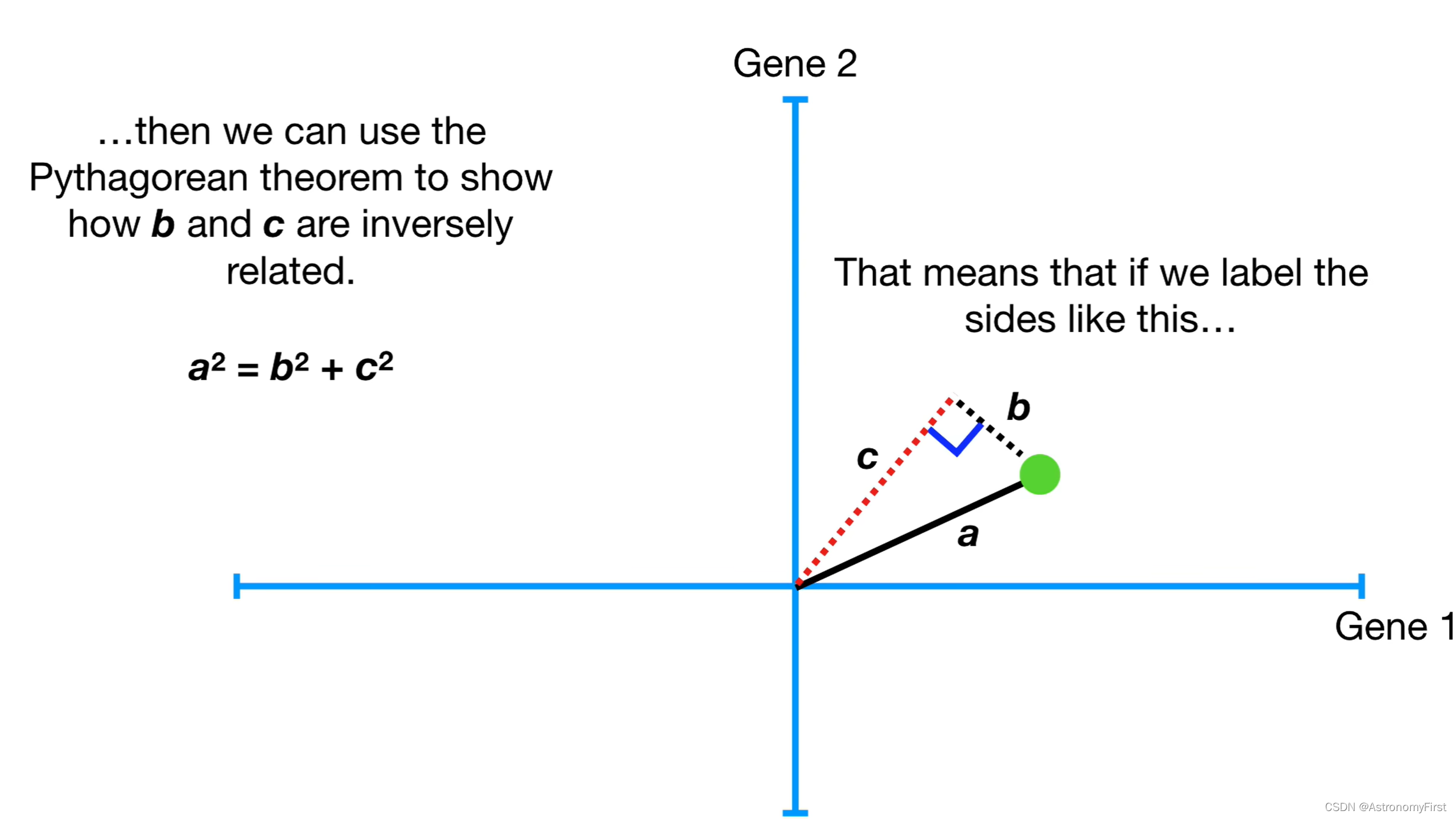
直观地讲,最小化b,即点到直线的距离,是合理的;但是实际上c,即投影点到原点的距离是更容易计算的,所以PCA找到拟合线是通过最大化投影点到原点距离的平方和来实现的。
9>以对于下图中左边这条直线,PCA将各个数据点投影到该直线上,并计算各个投影点到原点的距离平方和并累计:d1^2+d2^2+d3^2+d4^2+d5^2+d6^2=sum of squared distances(简称为SSD)
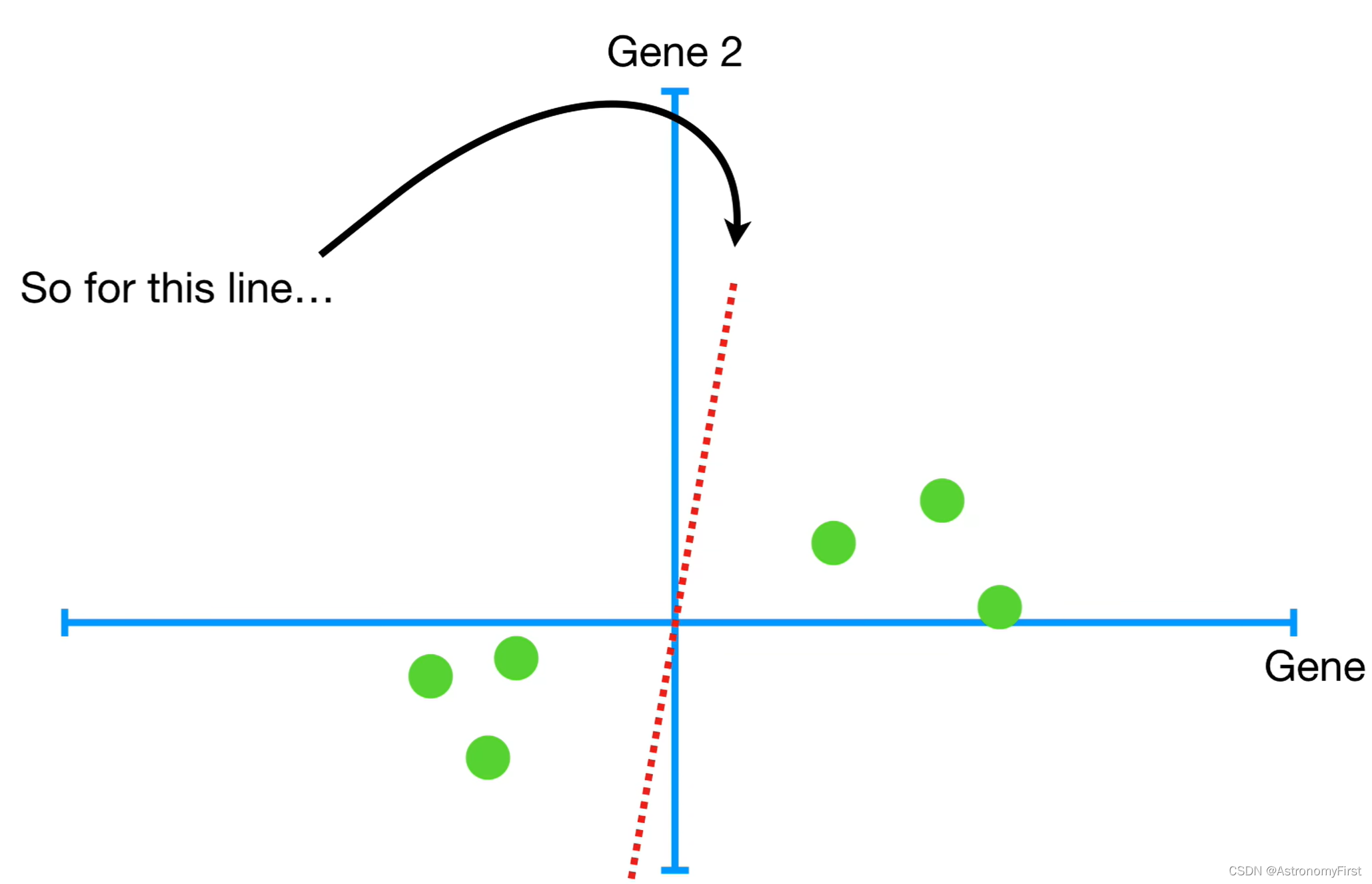
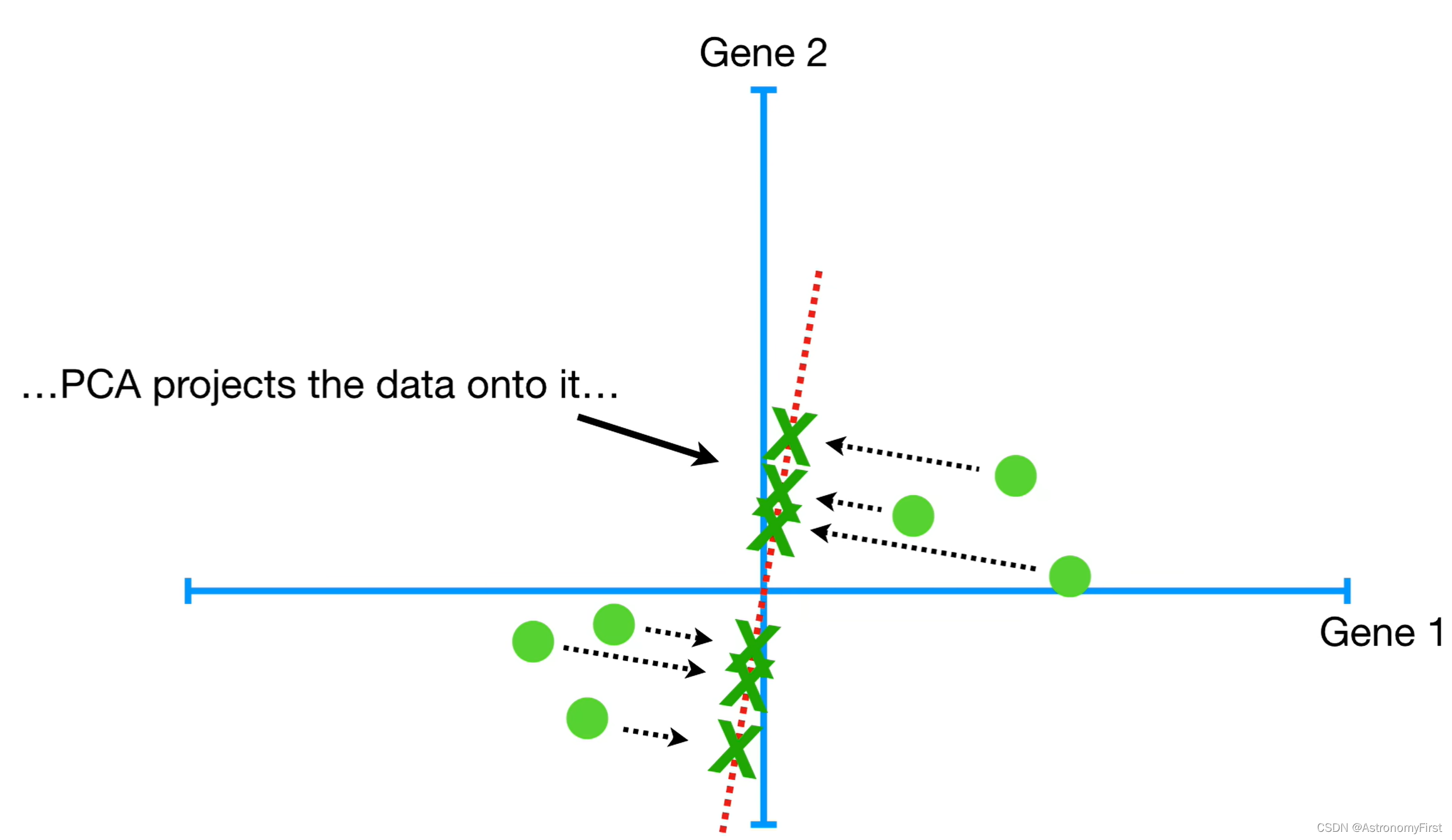
10>这时我们就可以旋转这条直线,不断计算距离和,直到找到一条有着最大的投影点到原点距离平方和的线,而这条线就叫做主成分1(即PC1)
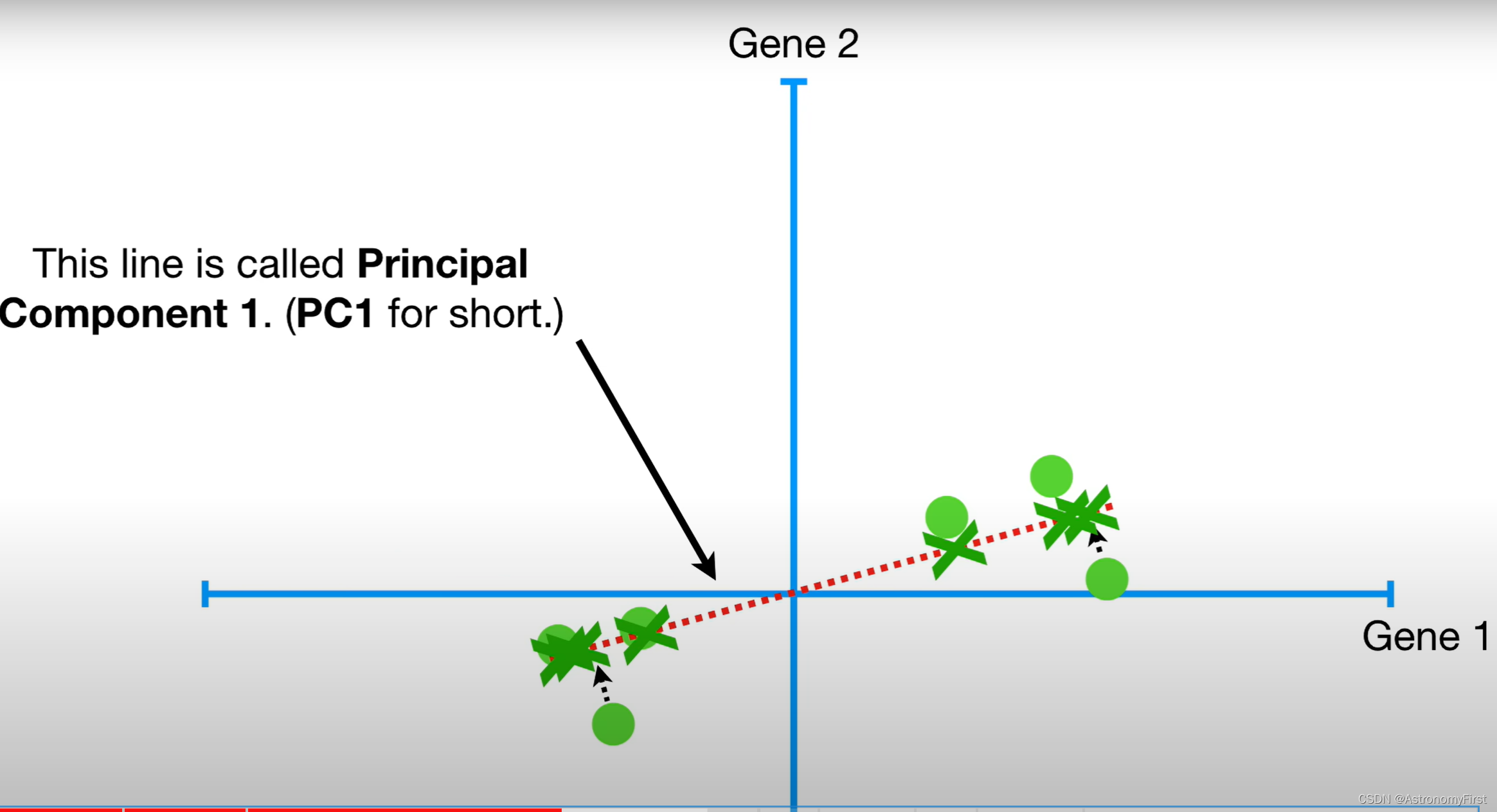
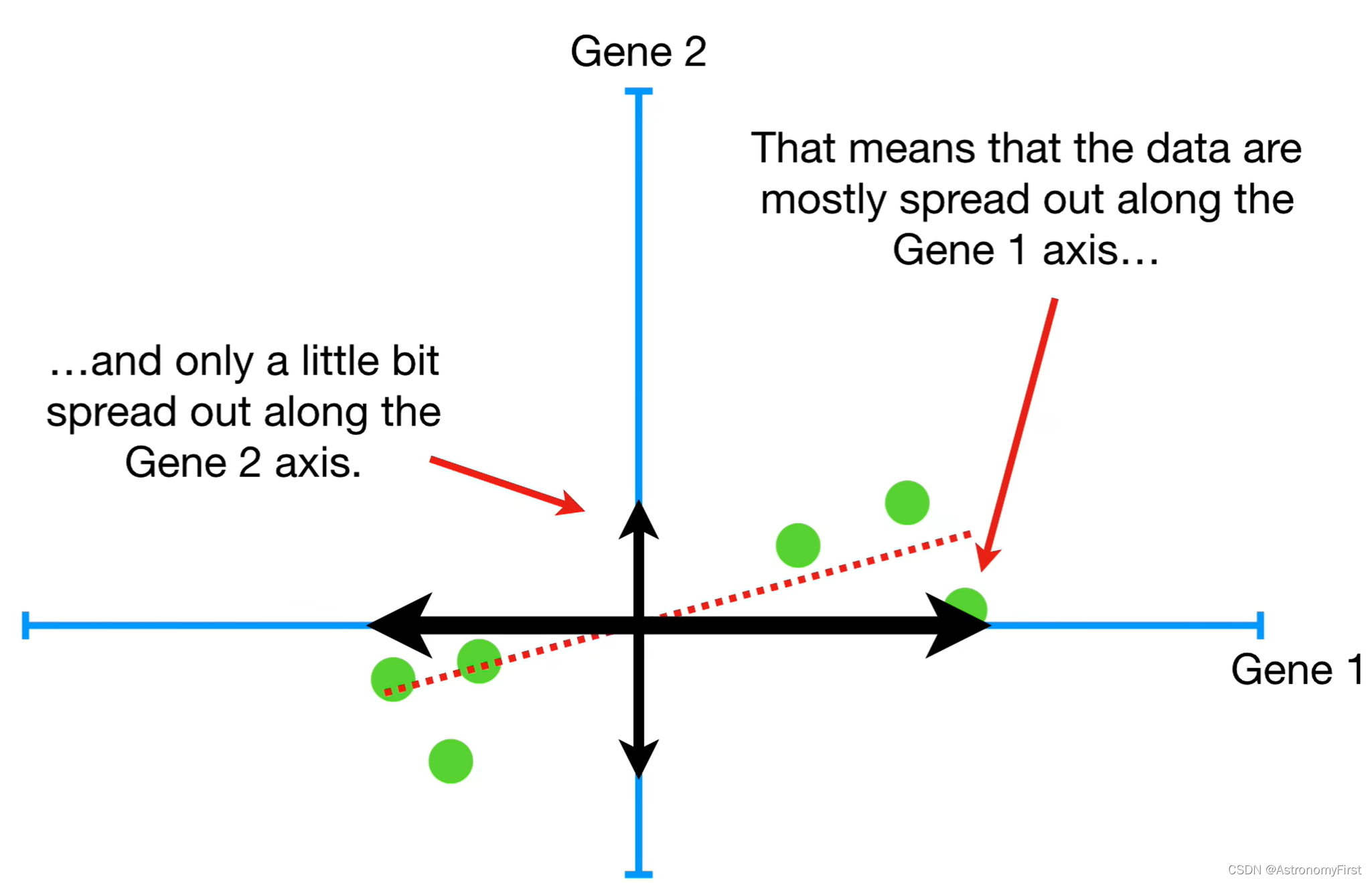
11>我们假设PC1的斜率为0.25,因此,我们沿着基因1轴每移动4个单位,我们就需要沿着基因2上升一个单位。这也就意味着数据大部分是沿着基因1轴所分布的,而沿着基因2轴只扩散了一点点。
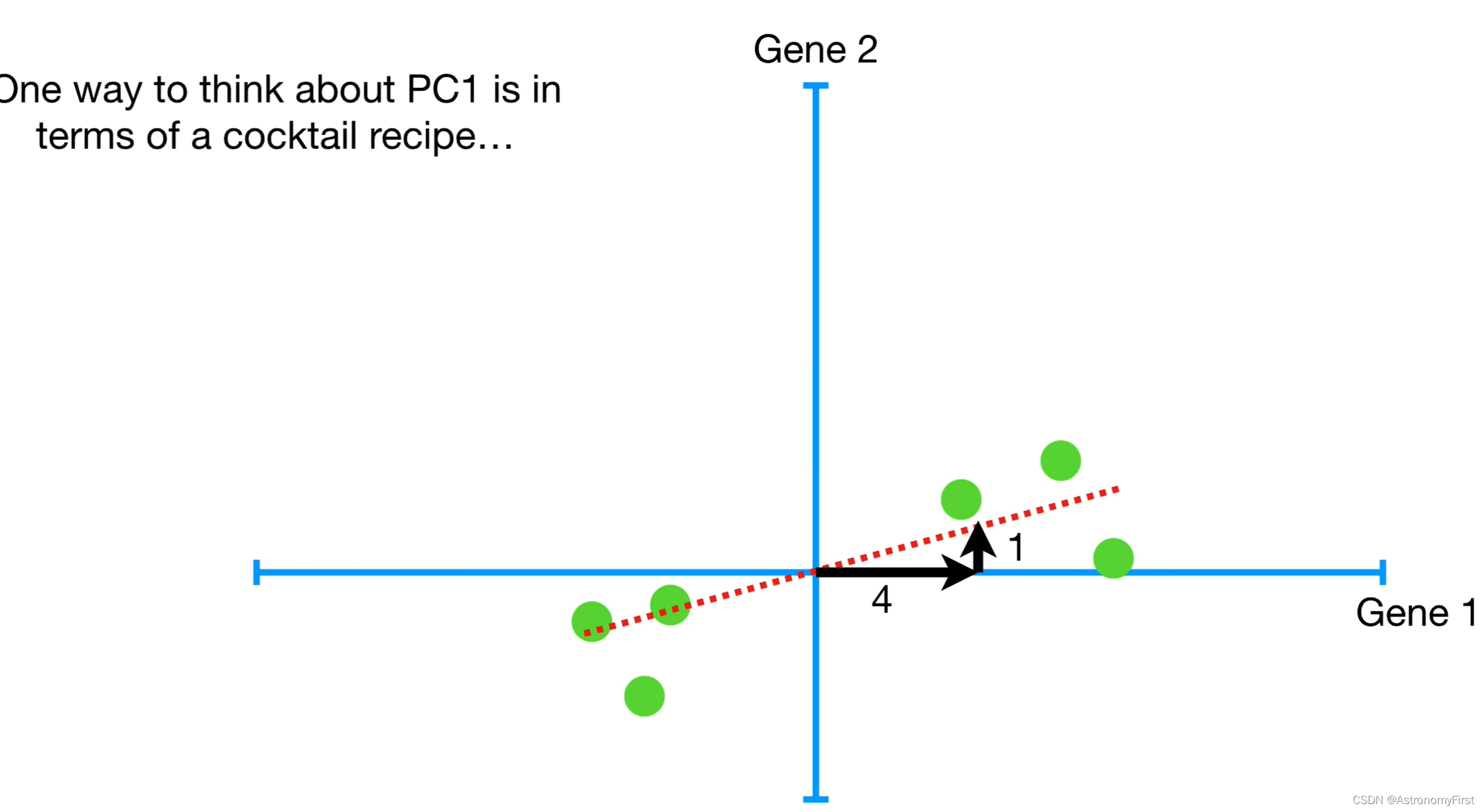
12>这样讲可能比较抽象,因此有一种理解PC1的方法就是想象成鸡尾酒的配方。为了制作PC1,需要混合四份的基因2和一份的基因1。基因1对基因2的比例,可以告诉我们在描述数据如何分布的时候,基因1对数据分布的影响是更大的。
13>特征向量、特征值和荷载得分
假设PC1上有一段如下图的向量。它的长度为1的平方和4的平方的和开根号。我们将该向量除以它自身的长度就会得到长度为1的向量,同时对应的黑色线段也要进行相同的操作
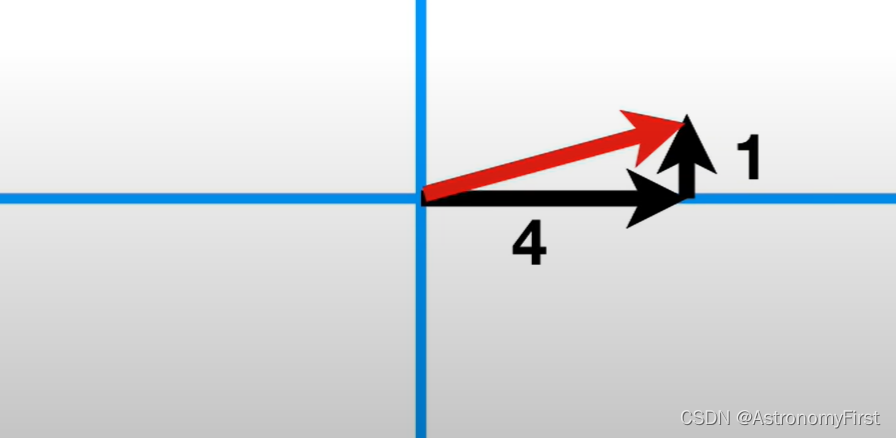
我们就可以得到如下图的结果,这个单位向量由0.97(4/4.12)个基因1和0.24(1/4.12)基因2所组成,被称为PC1的奇异向量(即特征向量),对应的每个基因的比例(0.97和0.242)被称为荷载得分。而PC1的特征值为SSD/n(n为样本的数量)。
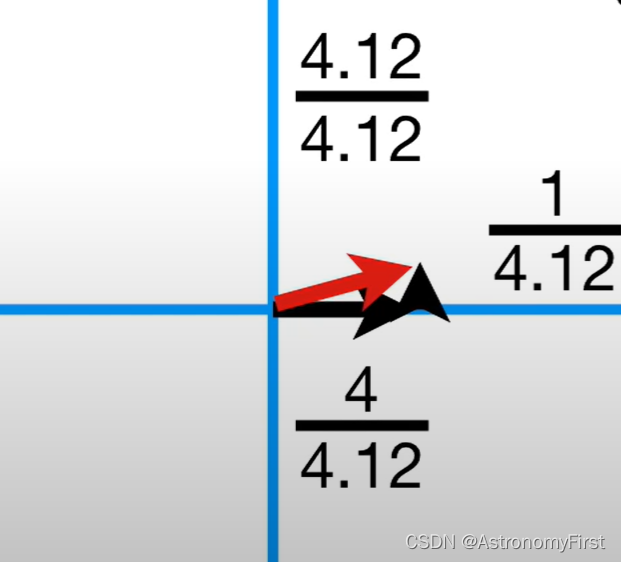
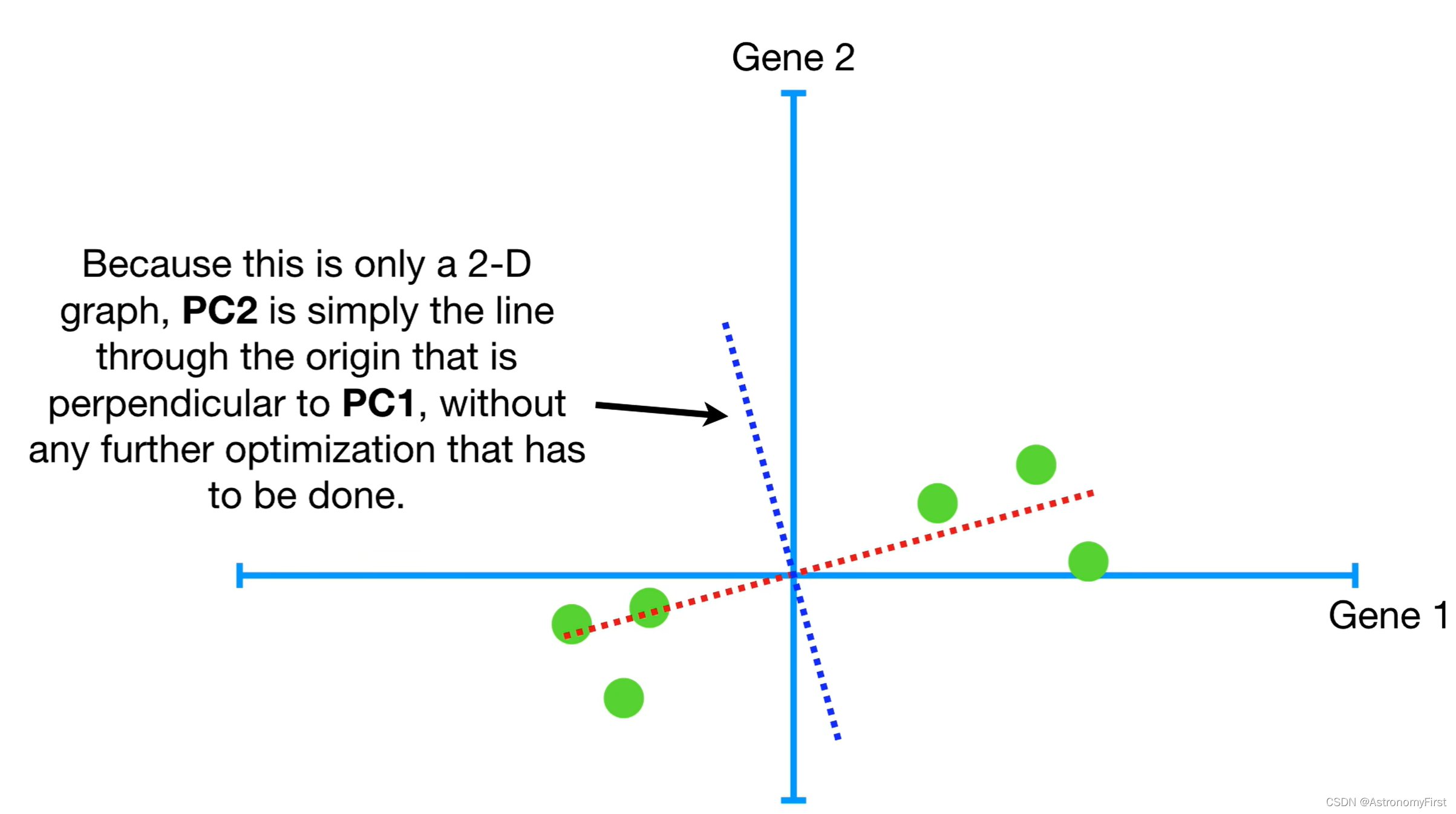
14>因为这只是一个二维的图,因此PC2就是一条过原点的线,垂直于PC1,没有更多做的优化了。
2.绘制PCA图
要绘制最终的PCA图,我们只需要旋转所有的内容,使PC1呈水平的状态就可以了。然后我们用投影点来定位PCA图中的样本位置就可以了。比如样本6的位置如下图确定
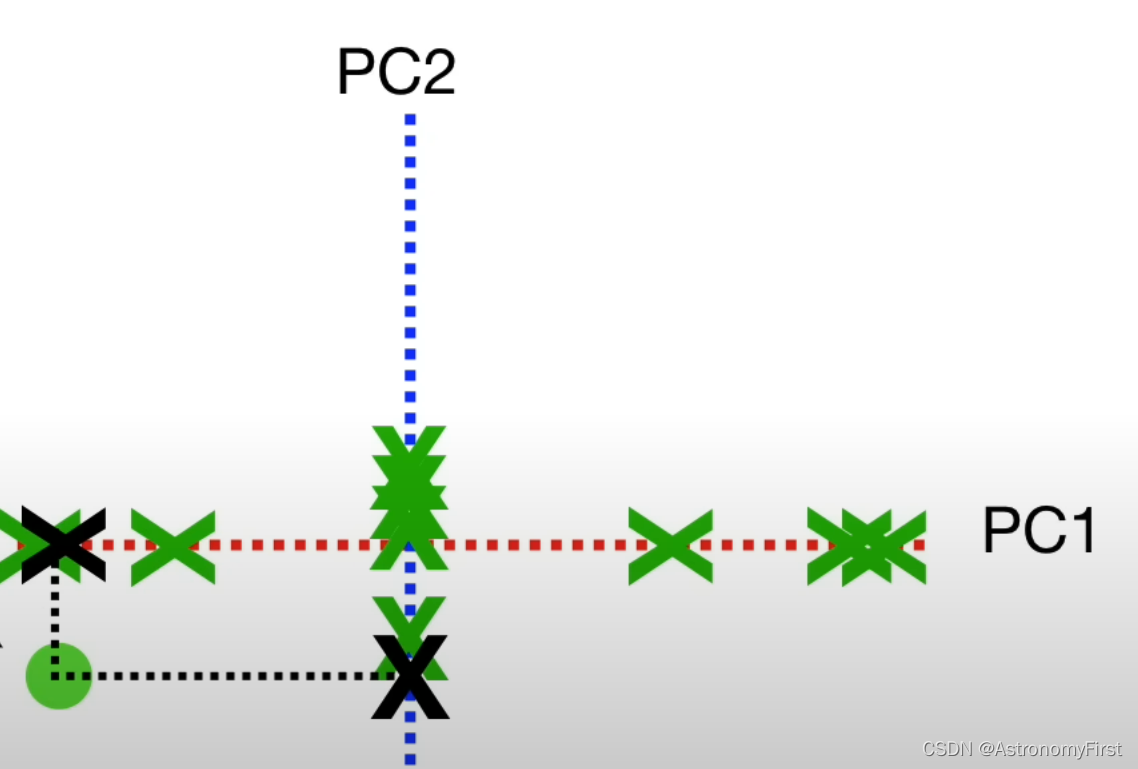
就可以得到所有点的PCA图了,如下:
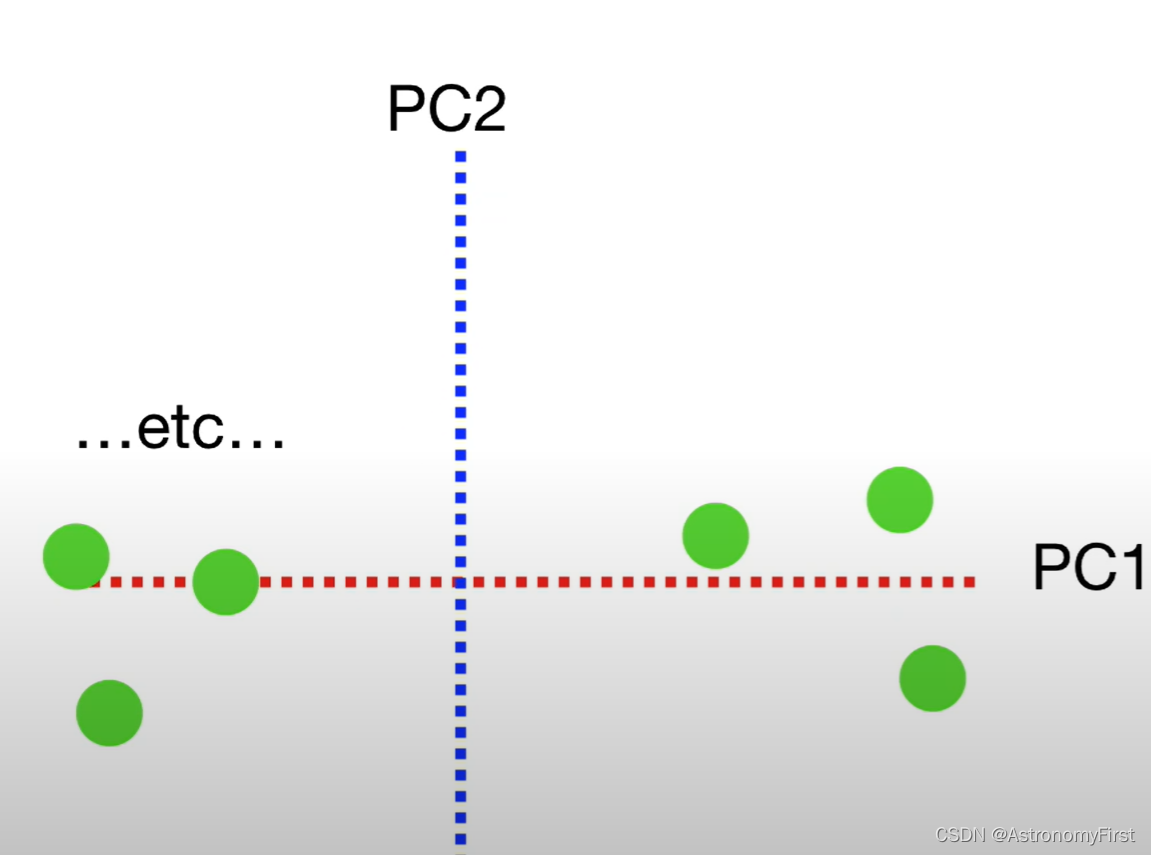
三.二维数据降维实例
1.代码
def PCA():
data = np.array([
[2.5, 2.4],[0.5, 0.7],[2.2, 2.9],[1.9, 2.2],[3.1, 3.0],
[2.3, 2.7],[2.0, 1.6],[1.0, 1.1],[1.5, 1.6],[1.1, 0.9]
])
# 计算均值向量
mean = [sum(x) / len(data) for x in zip(*data)]
# 数据去中心化
data_center = data - mean
# 初始化协方差矩阵为0
covariance_matrix = [[0, 0], [0, 0]]
# 计算协方差矩阵
for i in range(len(data)):
diff = [data[i][j] - mean[j] for j in range(len(mean))]
for j in range(len(mean)):
for k in range(len(mean)):
covariance_matrix[j][k] += diff[j] * diff[k]
# 将协方差矩阵的每个元素除以样本数减一以得到无偏估计的协方差
for j in range(len(mean)):
for k in range(len(mean)):
covariance_matrix[j][k] /= len(data) - 1 # 无偏估计使用n-1作为分母
# 输出结果
print("均值向量:")
print(mean)
#("协方差矩阵:")
covariance_matrix1 = np.matrix(covariance_matrix)
print(covariance_matrix1)
eigenvalues, eigenvectors = np.linalg.eig(covariance_matrix1)
print("特征值:")
print(eigenvalues)
print("特征向量:")
print(eigenvectors)
redata_center = np.matrix(data_center)
# 排序特征值和特征向量
idx = eigenvalues.argsort()[::-1]
eigenvalues = eigenvalues[idx]
eigenvectors = eigenvectors[:, idx]
# 选择第一个主成分(即最大特征值对应的特征向量)
principal_component = eigenvectors[:, 0]
print("\n第一个主成分(特征向量):")
print(principal_component)
print("\n降维后的数据:")
print(np.dot(redata_center, principal_component))2.输出结果
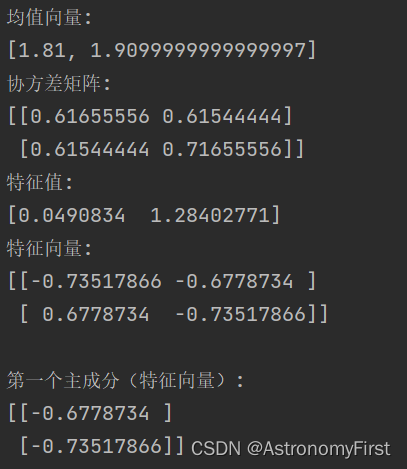

3.结果分析
由输出的结果可知,我们通过一系列的操作。先求出数据集的协方差矩阵,再通过协方差矩阵求出相应的特征值和特征向量;这时,就以特征值大的那个特征向量为PC1,通过矩阵的运算将原先的二维数据降维至一维数据,成功完成了数据的降维操作。
四.实验总结
本次实验通过PCA(主成分分析)技术,成功将二维数据降维至一维。实验过程中,观察到数据在降维后的主要特征被有效保留,同时减少了数据的复杂性。PCA的应用使得我们能够更加直观地理解数据的内在结构,并有助于后续的数据分析和模型训练。
实验结果验证了PCA在降维领域的强大功能,特别是在处理高维数据时,其能够显著减少计算成本,同时保持数据的主要信息。通过本次实验,加深了我对PCA原理和应用的理解。
总之,通过本次的实验,我对数据降维的大致流程有了清晰的认识,以及如何不调用numpy的相应的函数实现协方差矩阵的运算。也清晰地认识到了数据降维的好处。





















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








