Large Margin Classification
Optimization Objective
在logistic回归中,cost function使用了sigmoid函数,从而将θTx的值映射到(0 , 1)范围内。 在SVM中提出
了另一种函数cost来替代sigmoid函数,如图:

上图中曲线部分是sigmoid函数,而两段线段组成的部分就是新提出的cost函数,它也满足值域在(0,1)
内并且是单调的,区别是当z>1或<-1时值为0。
如果我们把cost function的前半部分设为A,后半部分设为B,那么它的形式为A+λB。而在SVM中我们要把它变换成CA+B的形式。(实际没有本质区别,C = 1/λ)
新的costfunction为:
Large Margin Intuition
在SVM中我们对θTx的值有更高的期待,从>0到>1,<0到<-1:
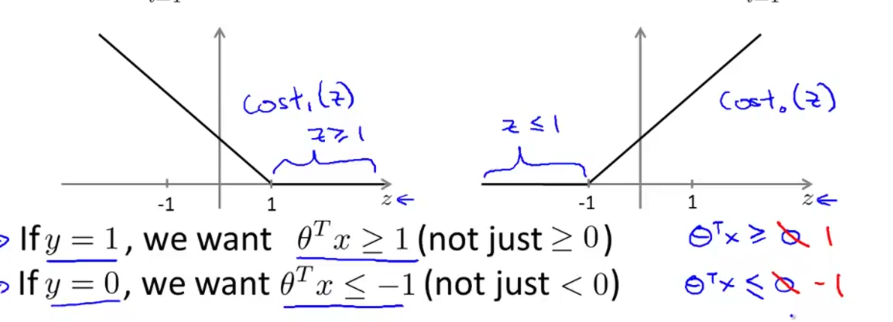
假设我们将C设置的非常大,那就使得对于所有的y = 1的数据,θTx都>1 ,反之都<-1,这样如果画出图像
来,decision boundary就不是原来的一条直线(θTx = 0),而是两条直线(θTx = 1,-1),而这两条直线
中间的部分就是margin(余量),这样鲁棒性就更好了。
C越小(λ越大)越不会被某个单一点影响。
Mathematics Behind Large Margin Classification
首先回忆一下向量知识
向量点乘:a . b = |a| * |b| * cos θ
向量长度: |a| = sqrt( a1^2 + a2^2 )
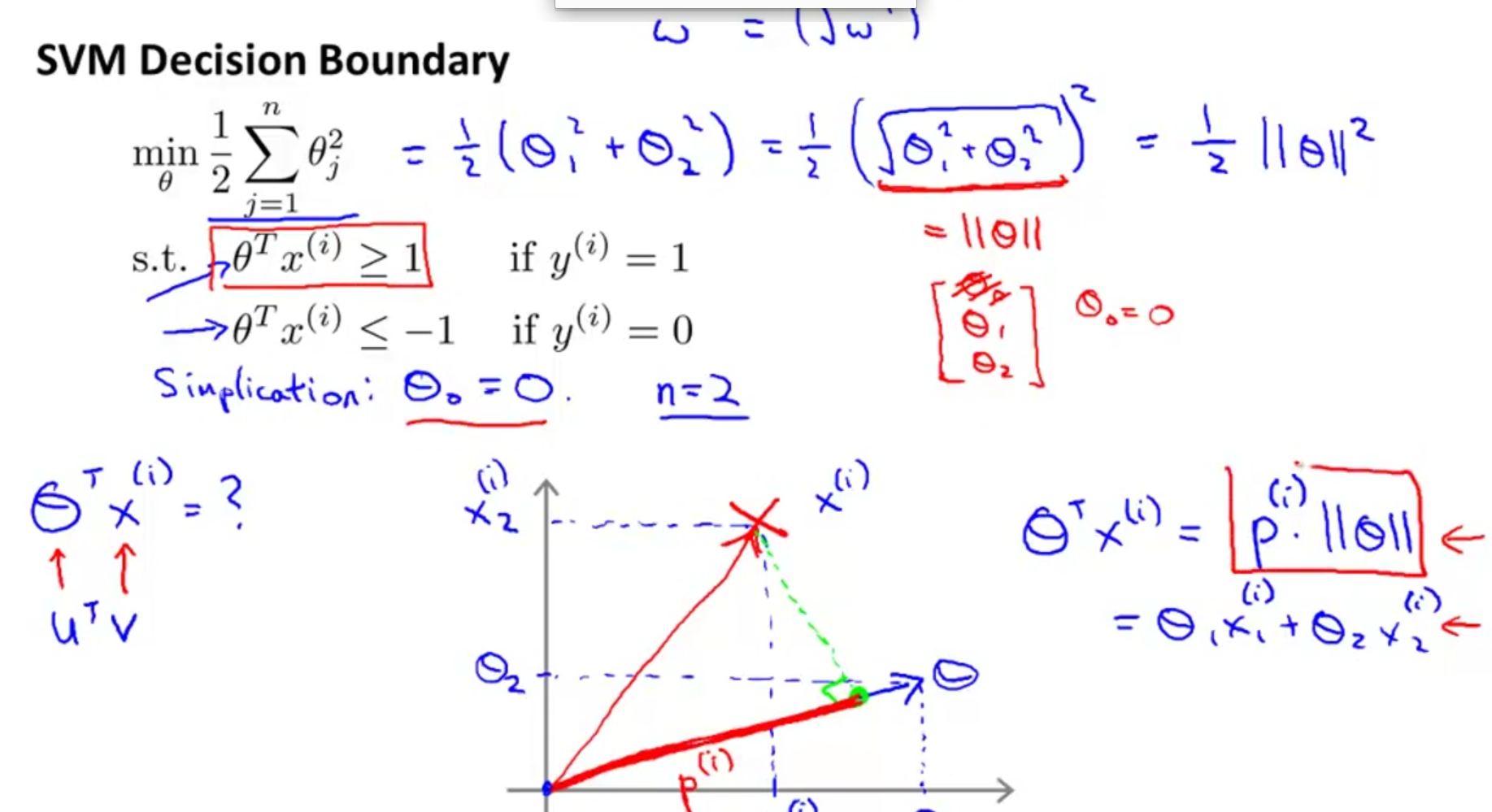
在cost function中,regularization部分实际就是|θ|,而θTx就是θ和x的数量积。
上图解释了为什么SVM可以保证margin尽可能大。上图黄色的线是decision boundary,那么θ就是和它垂
直的一条线,θTx(i)就是向量x(i)在θ上的投影长度*|θ|。
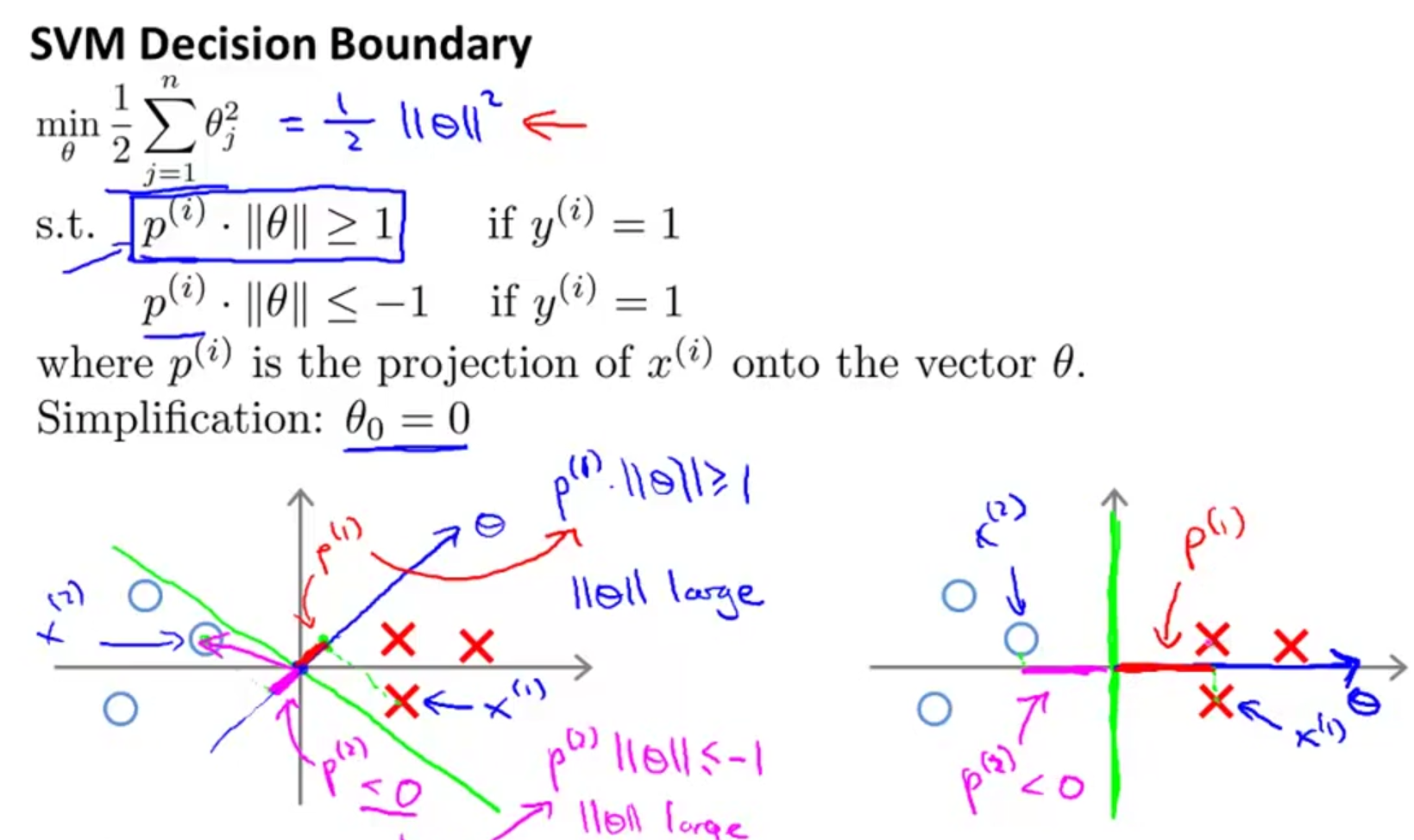
左图margin较小,因此各点到θ上的投影p都很小,而SVM要求p(i) * |θ| 都>=1或<=-1,当p很小时|θ|就需
要很大,而因为regularization的限制,θ不可以太大,p就需要足够大,这就保证了margin足够大(右图)。
上图中假设θ0 = 0,如果θ0不等于0,那么θ就不经过原点,但这不影响上面的证明过程。
Kernels
Kernels 1
在做非线性分类(decision boundary不是直线)时,一种方法是设计复杂的多项式X。这里提出一种新的方
法:另分类函数为 θ0 + θ1f1 + θ2f2 + θ3f3…….
f函数定义为:
其中l(i)为人为设定的landmark点。
该函数在x非常接近l时值为1,远离l时值为0。这个函数也被称为高斯核函数,也可记为k(l(i),x)。f函数图像
是一个山峰型的,l(i)点值为1,l(i)各方向朝0趋近,σ越小趋近的越快。
给定一个x和一些点l1,l2,l3….,按上述规则计算f1,f2,f3..,若θ0 + θ1f1 + θ2f2 + θ3f3>=0(θ0<0)则预测
为1,否则预测为0。
这样的结果是,在各个l点周围的x会预测为1,其余预测为0,这样就完成了非线性分类。
Kernels 2
如何选取这些landmark呢,一种方法是把所有的training set中的点(m个)做为landmark。这样对于每个x(i),我们可以计算出f(1)…..f(m),再添加一个f(0) = 1形成一个f向量。使用这个向量我们可以构成一个simple vector machine
将cost function改为:

因为f向量大小为m+1,因此后半部分的n = m(忽略θ0)
上图中许多运算操作都可以使用向量化和math tricks优化,而这些优化很多都不适用于其他算法,这也是SVM的不可替代性。
当出现过拟合时,减小C(增大λ)和增大σ(使f函数曲线更平滑)都可以减小过拟合。








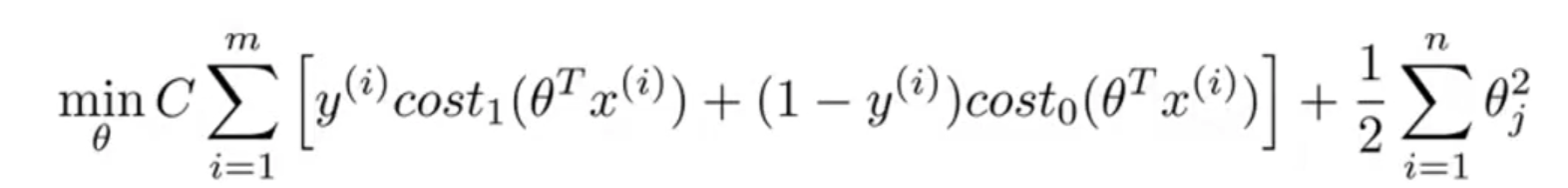
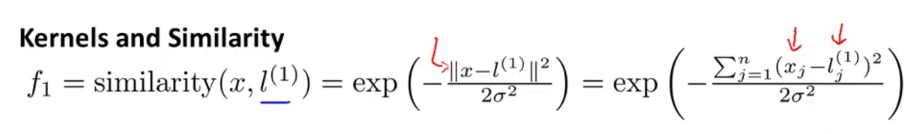














 1020
1020

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








