多元相关随机变量的生成

Longer2048

已于 2022-07-17 21:37:13 修改

410

分类专栏：线代文章标签：大数据线性代数

于 2022-07-17 11:47:29 首次发布

本文链接：https://blog.csdn.net/BeiErGeLaiDe/article/details/125828853

版权

线代专栏收录该内容

3 篇文章 0 订阅

订阅专栏

找了几天的资料，把国内外的思路整合了一下，共同学习。

一、引例：如何生成2个相关性为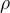 $\rho$ ，且服从标准正太分布 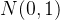$N(0,1)$ 的随机变量 $x_{1},x_{2}$ ？

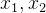答案：先随机生成2个独立 $(\rho=0)$ 的，服从标准正太分布 $N(0,1)$ 的随机变量 $z_{1},z_{2}$ 。

再考虑相关性，最终可以得到：

$\\x_{1}=z_{1} \\x_{2}=\rho z_{1}+\sqrt{1-p^2} z_{2}$

可以证明:

$\begin{align*} var(x_{1})&=var(z_{1})=1\\ var(x_{2})&=\rho^2var(z_{1})+(1+\rho^2)var(z_{2})=1 \\ cov(x_{1},x_{2})&=cov(z_{1},\rho z_{1}+\sqrt{1+\rho^2}z_{2})=cov(z_{1},\rho z_{1})=\rho \end{align*}$

因此 $x_{1},x_{2}$ 符合题目要求。

下面讲一下通用的思路，可以用来生成2个或多个有相关性的随机变量。

二、多元相关随机变量的生成：

题目：要求生成协方差矩阵为 $C_{n*n}$ 的多个符合正太分布的变量，即生成 $X=[X_{1},X_{2},X_{3},...,X_{n}]^T$ ，使得 $X\sim N(\mu ,C_x )$ ，注意这里的 $C_{x}$ 是协方差矩阵，不是相关性矩阵，其中 $\mu =[\mu _{1},\mu _{2},...,\mu _{n}]^T$ 为均值向量。

答案：首先生成符合标准正太分布的随机变量向量 $Z\sim N(0 ,1)$ ，则 $X=\mu+AZ$ 则为所求的随机变量向量（其中 $AA^T=C_{x}$ ）。

证明：

因为Z变量是随机生成的，因此其元素间的相关性=0，元素自身相关性为1，因此Z的协方差矩阵=相关性矩阵 $C_z=cov(Z)=\begin{bmatrix} [1,0,0],[0,1,0],[0,0,1] \end{bmatrix}=I$ ，是单位阵。

所以 $cov(X)=cov(\mu +AZ)=cov(CZ)=Acov(Z)A^T=AIA^T=AIA^T$

因此X的协方差矩阵 $C_x=cov(X)=AA^T$ 。

至此，问题就变成了：如何将协方差矩阵 $C_{x}$ 分解成矩阵*矩阵的转置，即 $C_x =AA^T$ ，得到矩阵A即可。

矩阵分解方法有多种，常见的可以分解成矩阵*矩阵的转置的方法：cholesky分解法（又称平方根分解），SVD，等等。

这部分后续再更新。

-------------------------------

吃完晚饭，继续更新。

在我另外一篇博客中讲到：生成协方差矩阵= $C_{n*n}$ 的多元随机变量时，也可以使用SVD分解法：

简要回顾SVD： $A_{m*n}=U\Sigma V^T$ ，SVD可以将一个矩阵（不要求必须是方阵）分解为左奇异矩阵 $U_{m*m}$ * 对角阵 $\Sigma_{m*n}$ * 右奇异矩阵 $V_{n*n}$ ，其中V是 $A^TA$ 的特征向量（注意公式中V有个转置操作），U是 $AA^T$ 的特征向量。 $\Sigma_{m*n}$ 是对角阵，对角元素是U、V的共同特征值，例如有三个特征值时： $\Sigma =[[\lambda_{1},0,0],[0,\lambda_{2},0],[0,0,\lambda_{3}]]$ 。

而上文讲到，只需要将协方差或相关性矩阵分解为矩阵*矩阵的转置，即可得到协方差矩阵为 $C_{x}$ 的多个随机变量。

现在问题变成：寻找一个矩阵A，使得协方差矩阵 $C_{x}=AA^T$ 。

对协方差矩阵 $C_{x}$ 进行SVD分解，考虑对称性可知 $U=V$ 。

SVD公式中的对角阵可以直接分解为矩阵*矩阵的转置： $\Sigma_{n*n}=\begin{bmatrix}\sigma_{1}&0\\0&\sigma_{2}\end{bmatrix}=D^TD$ ，其中 $D=\begin{bmatrix}\sqrt{\sigma_{1}}&0\\0&\sqrt{\sigma_{2}}\end{bmatrix}$ 。