高中数学：空间向量-各种位置关系的计算与证明

一、向量定义

既有大小，又有方向的一个量

二、基本的运算

1、线性运算

1.1、向量加法运算

1.2、向量减法运算

向量是可以随便平移的！！！

1.3、共线向量

$\lambda$的正负号，决定向量的方向！

1.4、向量分解

简单的理解为，条条大路通罗马，起点和终点相同，那么，分解就是正确的！！

2、数量积运算

公式变形
这个常用来求：线线角、线面角、面面角

3、建空间坐标系

注意：三个坐标轴要两两垂直。
我们在题目中建系的时候，一定要找两两垂直的三条直线进行建系，否则错误。

三步骤：
1、建系
三条坐标轴两两垂直
2、确定点坐标
基本的几何知识
3、求向量
终点减起点：$\overrightarrow{AB}=B坐标-A坐标$

4、向量坐标运算

三、常见题型

1、平行垂直的证明

1.1、情况分类

线线关系，线面关系，面面关系

1.2、空间向量表示线

终点坐标减去起点坐标得到空间向量
用方向向量表示线

1.3、空间向量表示面

法向量表示面

法向量的求法：
这里注意，因为法向量有无数个，所以，三元方程组，只有两个式子
我们可以令x、y、z中任意一个为一个值，在求出另外两个值

1.4、证明平行和垂直的理论依据

1.5、习题

证明线线垂直、线面平行
解析：建系、向量坐标运算

2、求角度

2.1、线线角

2.1、线面角

2.3、面面角

注意，求cosx的时候，需要判断正负号。

2.4、练习

1、求线线角

2、求线面角

3、求面面角

3、求距离

情况分类，其中线线距离不做要求

3.1、点到线的距离-向量到直线的投影

关键点：求出直线的单位向量u

3.2、点到面的距离

关键点，求出面的法向量

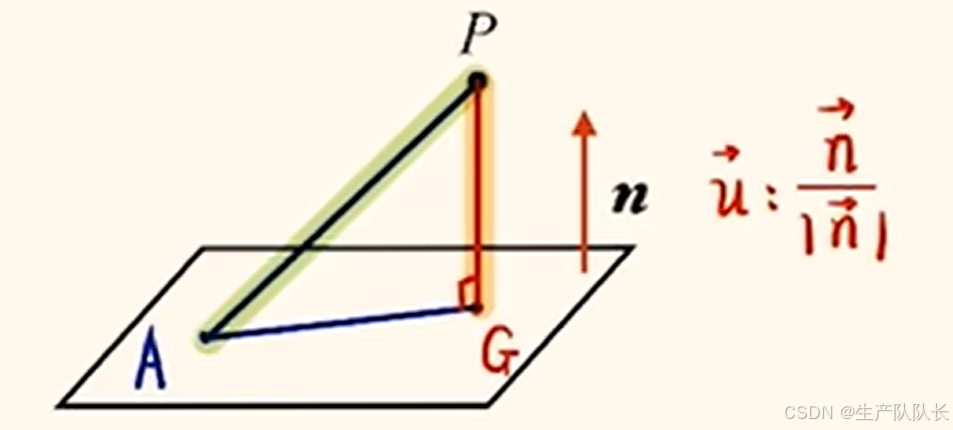
3.3、公式总结

3.4、练习

1、点到线的距离
求出ME的单位向量，然后就是向量坐标运算即可。

2、求点到面的距离
建系
求面的法向量
套公式即可