作者 | 远洋之帆 编辑 | 汽车人
原文链接:https://zhuanlan.zhihu.com/p/672855397
点击下方卡片,关注“自动驾驶之心”公众号
ADAS巨卷干货,即可获取
点击进入→自动驾驶之心【规划控制】技术交流群
本文只做学术分享,如有侵权,联系删文
本项目代码:
github.com/liangwq/robot_motion_planing
轨迹约束中的软硬约束
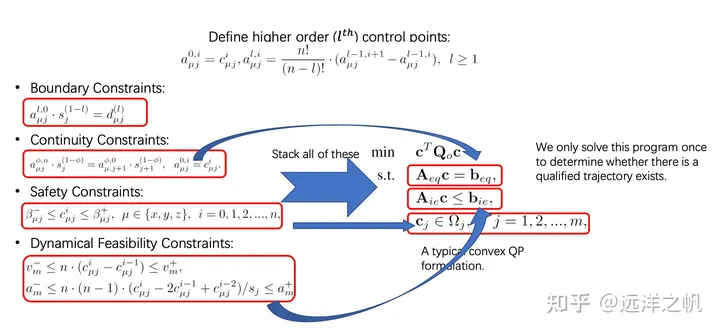
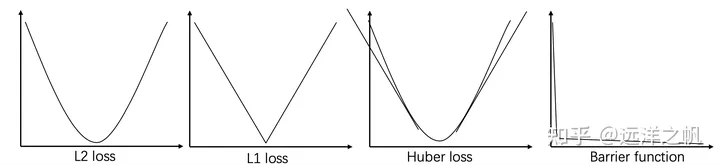
前面的几篇文章已经介绍了,轨迹约束的本质就是在做带约束的轨迹拟合。输入就是waypoint点list,约束条件有两种硬约束和软约束。所谓硬约束对应到数学形式就是代价函数,硬约束对应的就是最优化秋季的约束条件部分。对应到物理意义就是,为了获得机器人可行走的安全的轨迹有:
把轨迹通过代价函数推离障碍物的方式
给出障碍物之间的可行走凸包走廊,通过硬约束让机器人轨迹必须在凸包走廊行走

Bezier曲线拟合轨迹
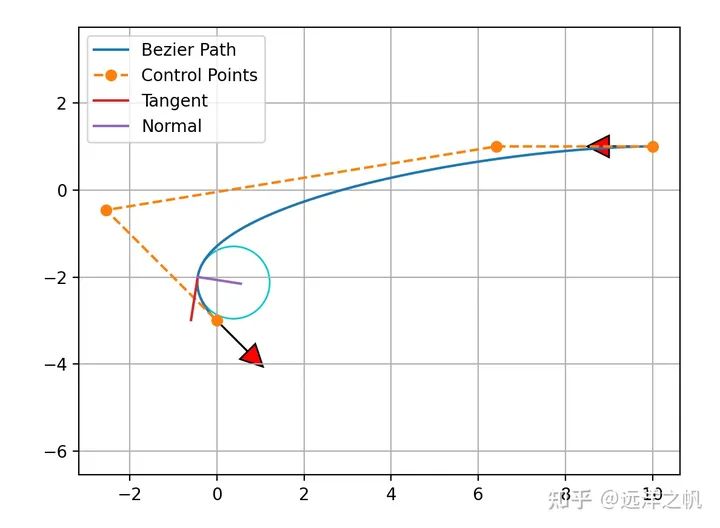
前面已经一篇文章介绍过贝赛尔曲线拟合的各种优点:
端点插值。贝塞尔曲线始终从第一个控制点开始,结束于最后一个控制点,并且不会经过任何其他控制点。
凸包。贝塞尔曲线 ( ) 由一组控制点 完全限制在由所有这些控制点定义的凸包内。
速度曲线。贝塞尔曲线 ( ) 的导数曲线 ′( ) 被称为速度曲线,它也是一个由控制点定义的贝塞尔曲线,其中控制点为 ∙ ( +1− ),其中 是阶数。
固定时间间隔。贝塞尔曲线始终在 [0,1] 上定义。
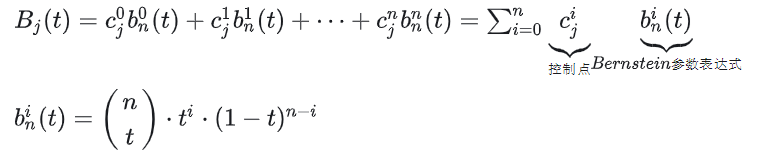
上面的两个表达式对应的代码实现如下:
def bernstein_poly(n, i, t):
"""
Bernstein polynom.
:param n: (int) polynom degree
:param i: (int)
:param t: (float)
:return: (float)
"""
return scipy.special.comb(n, i) * t ** i * (1 - t) ** (n - i)
def bezier(t, control_points):
"""
Return one point on the bezier curve.
:param t: (float) number in [0, 1]
:param control_points: (numpy array)
:return: (numpy array) Coordinates of the point
"""
n = len(control_points) - 1
return np.sum([bernstein_poly(n, i, t) * control_points[i] for i in range(n + 1)], axis=0)要用Bezier曲线来表示一段曲线,上面已经给出了表达式和代码实现,现在缺的就是给定控制点,把控制点带进来用Bezier曲线表达式来算出给定终点和结束点中需要画的点坐标。下面代码给出了4个控制点、6个控制点的Bezier曲线实现;其中为了画曲线需要算170个线上点。代码如下:
def calc_4points_bezier_path(sx, sy, syaw, ex, ey, eyaw, offset):
"""
Compute control points and path given start and end position.
:param sx: (float) x-coordinate of the starting point
:param sy: (float) y-coordinate of the starting point
:param syaw: (float) yaw angle at start
:param ex: (float) x-coordinate of the ending point
:param ey: (float) y-coordinate of the ending point
:param eyaw: (float) yaw angle at the end
:param offset: (float)
:return: (numpy array, numpy array)
"""
dist = np.hypot(sx - ex, sy - ey) / offset
control_points = np.array(
[[sx, sy],
[sx + dist * np.cos(syaw), sy + dist * np.sin(syaw)],
[ex - dist * np.cos(eyaw), ey - dist * np.sin(eyaw)],
[ex, ey]])
path = calc_bezier_path(control_points, n_points=170)
return path, control_points
def calc_6points_bezier_path(sx, sy, syaw, ex, ey, eyaw, offset):
"""
Compute control points and path given start and end position.
:param sx: (float) x-coordinate of the starting point
:param sy: (float) y-coordinate of the starting point
:param syaw: (float) yaw angle at start
:param ex: (float) x-coordinate of the ending point
:param ey: (float) y-coordinate of the ending point
:param eyaw: (float) yaw angle at the end
:param offset: (float)
:return: (numpy array, numpy array)
"""
dist = np.hypot(sx - ex, sy - ey) * offset
control_points = np.array(
[[sx, sy],
[sx + 0.25 * dist * np.cos(syaw), sy + 0.25 * dist * np.sin(syaw)],
[sx + 0.40 * dist * np.cos(syaw), sy + 0.40 * dist * np.sin(syaw)],
[ex - 0.40 * dist * np.cos(eyaw), ey - 0.40 * dist * np.sin(eyaw)],
[ex - 0.25 * dist * np.cos(eyaw), ey - 0.25 * dist * np.sin(eyaw)],
[ex, ey]])
path = calc_bezier_path(control_points, n_points=170)
return path, control_points
def calc_bezier_path(control_points, n_points=100):
"""
Compute bezier path (trajectory) given control points.
:param control_points: (numpy array)
:param n_points: (int) number of points in the trajectory
:return: (numpy array)
"""
traj = []
for t in np.linspace(0, 1, n_points):
traj.append(bezier(t, control_points))
return np.array(traj)有了一段Bezier曲线的拟合方式,接下来要做的就是如何生成多段Bezier曲线合成一条轨迹;并且是需要可以通过代价函数方式(软约束)+必须经过指定点+制定点衔接要连续(硬约束)来生成一条光滑的轨迹曲线。
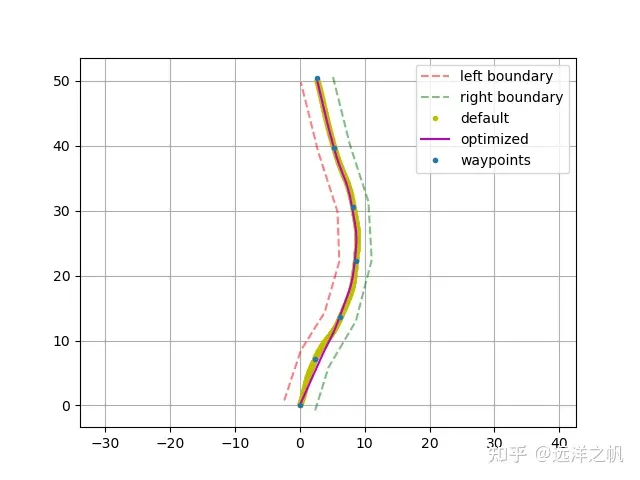
多段Bezier曲线生成代码如下,其实原理很简单,给定多个waypoint点,每相邻两个wayponit生成一段Bezizer曲线,代码如下:
# Bezier path one as per the approach suggested in
# https://users.soe.ucsc.edu/~elkaim/Documents/camera_WCECS2008_IEEE_ICIAR_58.pdf
def cubic_bezier_path(self, ax, ay):
dyaw, _ = self.calc_yaw_curvature(ax, ay)
cx = []
cy = []
ayaw = dyaw.copy()
for n in range(1, len(ax)-1):
yaw = 0.5*(dyaw[n] + dyaw[n-1])
ayaw[n] = yaw
last_ax = ax[0]
last_ay = ay[0]
last_ayaw = ayaw[0]
# for n waypoints, there are n-1 bezier curves
for i in range(len(ax)-1):
path, ctr_points = calc_4points_bezier_path(last_ax, last_ay, ayaw[i], ax[i+1], ay[i+1], ayaw[i+1], 2.0)
cx = np.concatenate((cx, path.T[0][:-2]))
cy = np.concatenate((cy, path.T[1][:-2]))
cyaw, k = self.calc_yaw_curvature(cx, cy)
last_ax = path.T[0][-1]
last_ay = path.T[1][-1]
return cx, cy代价函数计算包括:曲率代价 + 偏差代价 + 距离代价 + 连续性代价,同时还有边界条件,轨迹必须在tube内的不等式约束,以及问题优化求解。具体代码实现如下:
# Objective function of cost to be minimized
def cubic_objective_func(self, deviation):
ax = self.waypoints.x.copy()
ay = self.waypoints.y.copy()
for n in range(0, len(deviation)):
ax[n+1] -= deviation[n]*np.sin(self.waypoints.yaw[n+1])
ay[n+1] += deviation[n]*np.cos(self.waypoints.yaw[n+1])
bx, by = self.cubic_bezier_path(ax, ay)
yaw, k = self.calc_yaw_curvature(bx, by)
# cost of curvature continuity
t = np.zeros((len(k)))
dk = self.calc_d(t, k)
absolute_dk = np.absolute(dk)
continuity_cost = 10.0 * np.mean(absolute_dk)
# curvature cost
absolute_k = np.absolute(k)
curvature_cost = 14.0 * np.mean(absolute_k)
# cost of deviation from input waypoints
absolute_dev = np.absolute(deviation)
deviation_cost = 1.0 * np.mean(absolute_dev)
distance_cost = 0.5 * self.calc_path_dist(bx, by)
return curvature_cost + deviation_cost + distance_cost + continuity_cost
# Minimize objective function using scipy optimize minimize
def optimize_min_cubic(self):
print("Attempting optimization minima")
initial_guess = [0, 0, 0, 0, 0]
bnds = ((-self.bound, self.bound), (-self.bound, self.bound), (-self.bound, self.bound), (-self.bound, self.bound), (-self.bound, self.bound))
result = optimize.minimize(self.cubic_objective_func, initial_guess, bounds=bnds)
ax = self.waypoints.x.copy()
ay = self.waypoints.y.copy()
if result.success:
print("optimized true")
deviation = result.x
for n in range(0, len(deviation)):
ax[n+1] -= deviation[n]*np.sin(self.waypoints.yaw[n+1])
ay[n+1] += deviation[n]*np.cos(self.waypoints.yaw[n+1])
x, y = self.cubic_bezier_path(ax, ay)
yaw, k = self.calc_yaw_curvature(x, y)
self.optimized_path = Path(x, y, yaw, k)
else:
print("optimization failure, defaulting")
exit()带障碍物的Bezier曲线轨迹生
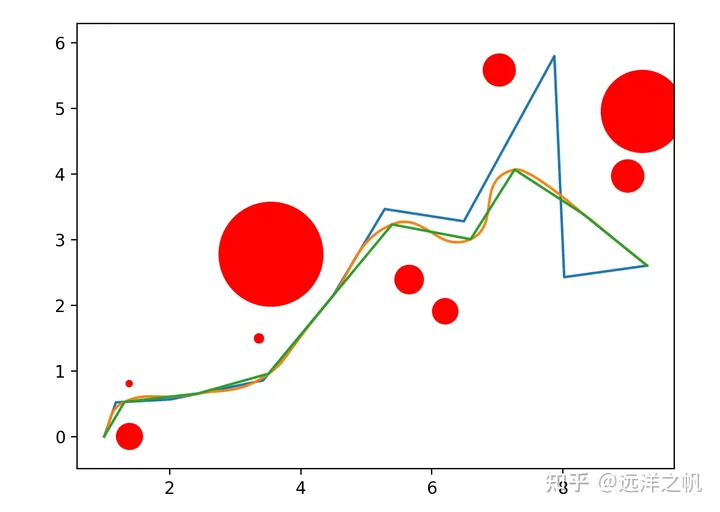
带有障碍物的场景,通过代价函数让生成的曲线远离障碍物。从而得到一条可以安全行走的轨迹,下面是具体的代码实现。optimizer_k中lambda函数f就是在求解轨迹在经过障碍物附近时候的代价,penalty1、penalty2就是在求曲线经过障碍物附近的具体代价值;
b.arc_len(granuality=10)+B.arc_len(granuality=10)+m_k + penalty1 + penalty2就是轨迹的整体代价。for循环部分用scipy的optimize的minimize来求解轨迹。
def optimizer_k(cd, k, path, i, obs, curve_penalty_multiplier, curve_penalty_divider, curve_penalty_obst):
"""Bezier curve optimizer that optimizes the curvature and path length by changing the distance of p1 and p2 from
points p0 and p3, respectively. """
p_tmp = copy.deepcopy(path)
if i+3 > len(path)-1:
b = CubicBezier()
b.p0 = p_tmp[i]
x, y = calc_p1(p_tmp[i], p_tmp[i + 1], p_tmp[i - 1], i, cd[0])
b.p1 = Point(x, y)
x, y = calc_p2(p_tmp[i-1], p_tmp[i + 0], p_tmp[i + 1], i, cd[1])
b.p2 = Point(x, y)
b.p3 = p_tmp[i + 1]
B = CubicBezier()
else:
b = CubicBezier()
b.p0 = p_tmp[i]
x, y = calc_p1(p_tmp[i],p_tmp[i+1],p_tmp[i-1], i, cd[0])
b.p1 = Point(x, y)
x, y = calc_p2(p_tmp[i],p_tmp[i+1],p_tmp[i+2], i, cd[1])
b.p2 = Point(x, y)
b.p3 = p_tmp[i + 1]
B = CubicBezier()
B.p0 = p_tmp[i]
x, y = calc_p1(p_tmp[i+1], p_tmp[i + 2], p_tmp[i], i, 10)
B.p1 = Point(x, y)
x, y = calc_p2(p_tmp[i+1], p_tmp[i + 2], p_tmp[i + 3], i, 10)
B.p2 = Point(x, y)
B.p3 = p_tmp[i + 1]
m_k = b.max_k()
if m_k>k:
m_k= m_k*curve_penalty_multiplier
else:
m_k = m_k/curve_penalty_divider
f = lambda x, y: max(math.sqrt((x[0] - y[0].x) ** 2 + (x[1] - y[0].y) ** 2) * curve_penalty_obst, 10) if math.sqrt(
(x[0] - y[0].x) ** 2 + (x[1] - y[0].y) ** 2) < y[1] else 0
b_t = b.calc_curve(granuality=10)
b_t = zip(b_t[0],b_t[1])
B_t = B.calc_curve(granuality=10)
B_t = zip(B_t[0], B_t[1])
penalty1 = 0
penalty2 = 0
for o in obs:
for t in b_t:
penalty1 = max(penalty1,f(t,o))
for t in B_t:
penalty2 = max(penalty2,f(t,o))
return b.arc_len(granuality=10)+B.arc_len(granuality=10)+m_k + penalty1 + penalty2
# Optimize the initial path for n_path_opt cycles
for m in range(n_path_opt):
if m%2:
for i in range(1,len(path)-1):
x0 = [0.0, 0.0]
bounds = Bounds([-1, -1], [1, 1])
res = minimize(optimizer_p, x0, args=(path, i, obs, path_penalty), method='TNC', tol=1e-7, bounds=bounds)
x, y = res.x
path[i].x += x
path[i].y += y
else:
for i in range(len(path)-1,1):
x0 = [0.0, 0.0]
bounds = Bounds([-1, -1], [1, 1])
res = minimize(optimizer_p, x0, args=(path, i, obs, path_penalty), method='TNC', tol=1e-7, bounds=bounds)
x, y = res.x
path[i].x += x
path[i].y += y带飞行走廊的Bezier轨迹生成
得益于贝赛尔曲线拟合的优势,如果我们可以让机器人可行走的轨迹转成多个有重叠区域的凸多面体,那么轨迹完全位于飞行走廊内。
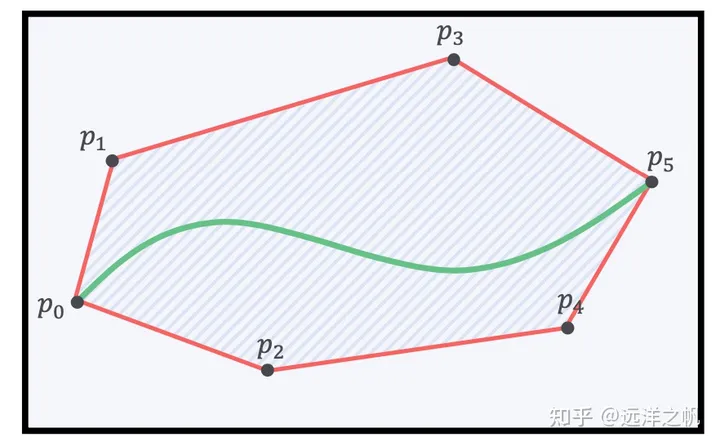
飞行走廊由凸多边形组成。
每个立方体对应于一段贝塞尔曲线。
此曲线的控制点被强制限制在多边形内部。
轨迹完全位于所有点的凸包内。
如何通过把障碍物地图生成可行凸包走廊
生成凸包走廊的方法目前有以下三大类的方法:
平行凸簇膨胀方法
从栅格地图出发,利用最小凸集生成算法,完成凸多面体的生成。其算法的思想是首先获得一个凸集,再沿着凸集的表面进行扩张,扩张之后再进行凸集检测,判断新扩张的集合是否保持为凸。一直扩张到不能再扩张为止,再提取凸集的边缘点,利用快速凸集生成算法,生成凸多面体。该算法的好处在于可以利用这种扩张的思路,将安全的多面体的体积尽可能的充满整个空间,因此获得的安全通道更大。但其也具有一定的缺点,就是计算量比较大,计算所需要的时间比较长,为了解决这个问题,在该文章中,又提出了采用GPU加速的方法,来加速计算。
基于凸分解的安全通道生成
基于凸分解的安全通道生成方法由四个步骤完成安全通道的生成,分别为:找到椭球、找到多面体、边界框、收缩。
半定规划的迭代区域膨胀
为了获取多面体,这个方法首先构造一个初始椭球,由一个以选定点为中心的单位球组成。然后,遍历障碍物,为每个障碍物生成一个超平面,该超平面与障碍物相切并将其与椭球分开。再次,这些超平面定义了一组线性约束,它们的交集是一个多面体。然后,可以在那个多面体中找到一个最大的椭球,使用这个椭球来定义一组新的分离超平面,从而定义一个新的多面体。选择生成分离超平面的方法,这样椭圆体的体积在迭代之间永远不会减少。可以重复这个过程,直到椭圆体的增长率低于某个阈值,此时我们返回多面体和内接椭圆体。这个方法具有迭代的思想,并且具有收敛判断的标准,算法的收敛快慢和初始椭球具有很大的关系。
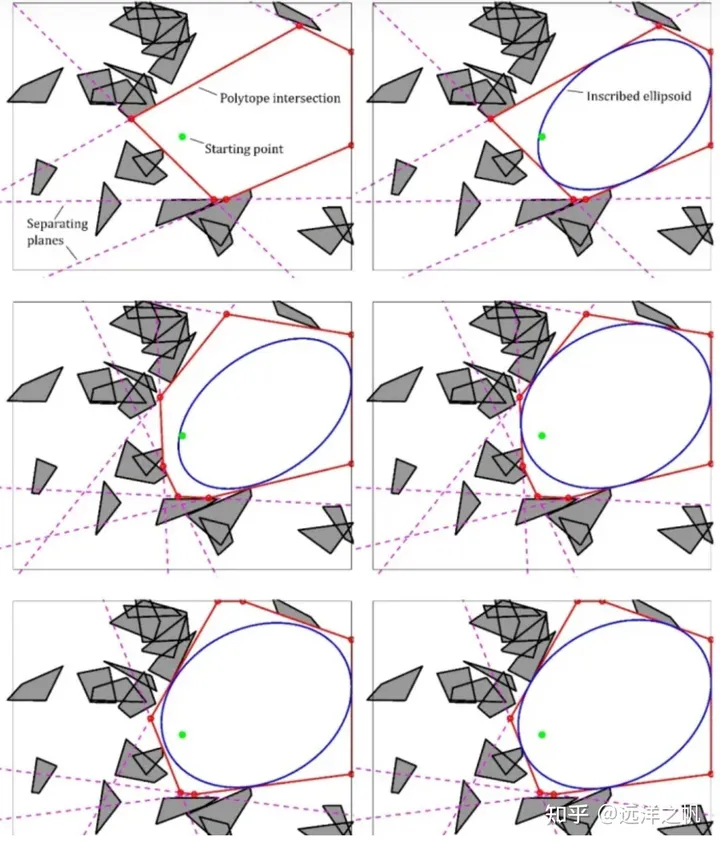
这篇文章介绍的是“半定规划的迭代区域膨胀”方法,具体代码实现如下:
# 根据输入路径对空间进行凸分解
def decomp(self, line_points: list[np.array], obs_points: list[np.array], visualize=True):
# 最终结果
decomp_polygons = list()
# 构建输入障碍物点的kdtree
obs_kdtree = KDTree(obs_points)
# 进行空间分解
for i in range(len(line_points) - 1):
# 得到当前线段
pf, pr = line_points[i], line_points[i + 1]
print(pf)
print(pr)
# 构建初始多面体
init_polygon = self.initPolygon(pf, pr)
print(init_polygon.getInterPoints())
print(init_polygon.getVerticals())
# 过滤障碍物点
candidate_obs_point_indexes = obs_kdtree.query_ball_point((pf + pr) / 2, np.linalg.norm([np.linalg.norm(pr - pf) / 2 + self.consider_range_, self.consider_range_]))
local_obs_points = list()
for index in candidate_obs_point_indexes:
if init_polygon.inside(obs_points[index]):
local_obs_points.append(obs_points[index])
# 得到初始椭圆
ellipse = self.findEllipse(pf, pr, local_obs_points)
# 根据初始椭圆构建多面体
polygon = self.findPolygon(ellipse, init_polygon, local_obs_points)
# 进行保存
decomp_polygons.append(polygon)
if visualize:
# 进行可视化
plt.figure()
# 绘制路径段
plt.plot([pf[1], pr[1]], [pf[0], pr[0]], color="red")
# 绘制初始多面体
verticals = init_polygon.getVerticals()
# 绘制多面体顶点
plt.plot([v[1] for v in verticals] + [verticals[0][1]], [v[0] for v in verticals] + [verticals[0][0]], color="blue", linestyle="--")
# 绘制障碍物点
plt.scatter([p[1] for p in local_obs_points], [p[0] for p in local_obs_points], marker="o")
# 绘制椭圆
ellipse_x, ellipse_y = list(), list()
for theta in np.linspace(-np.pi, np.pi, 1000):
raw_point = np.array([np.cos(theta), np.sin(theta)])
ellipse_point = np.dot(ellipse.C_, raw_point) + ellipse.d_
ellipse_x.append(ellipse_point[0])
ellipse_y.append(ellipse_point[1])
plt.plot(ellipse_y, ellipse_x, color="orange")
# 绘制最终多面体
# 得到多面体顶点
verticals = polygon.getVerticals()
# 绘制多面体顶点
plt.plot([v[1] for v in verticals] + [verticals[0][1]], [v[0] for v in verticals] + [verticals[0][0]], color="green")
plt.show()
return decomp_polygons
# 构建初始多面体
def initPolygon(self, pf: np.array, pr: np.array) -> Polygon:
# 记录多面体的平面
polygon_planes = list()
# 得到线段方向向量
dire = self.normalize(pr - pf)
# 得到线段法向量
dire_h = np.array([dire[1], -dire[0]])
# 得到平行范围
p_1 = pf + self.consider_range_ * dire_h
p_2 = pf - self.consider_range_ * dire_h
polygon_planes.append(Hyperplane(dire_h, p_1))
polygon_planes.append(Hyperplane(-dire_h, p_2))
# 得到垂直范围
p_3 = pr + self.consider_range_ * dire
p_4 = pf - self.consider_range_ * dire
polygon_planes.append(Hyperplane(dire, p_3))
polygon_planes.append(Hyperplane(-dire, p_4))
# 构建多面体
polygon = Polygon(polygon_planes)
return polygon
# 得到初始椭圆
def findEllipse(self, pf: np.array, pr: np.array, obs_points: list[np.array]) -> Ellipse:
# 计算长轴
long_axis_value = np.linalg.norm(pr - pf) / 2
axes = np.array([long_axis_value, long_axis_value])
# 计算旋转
rotation = self.vec2Rotation(pr - pf)
# 计算初始椭圆
C = np.dot(rotation, np.dot(np.array([[axes[0], 0], [0, axes[1]]]), np.transpose(rotation)))
d = (pr + pf) / 2
ellipse = Ellipse(C, d)
# 得到椭圆内的障碍物点
inside_obs_points = ellipse.insidePoints(obs_points)
# 对椭圆进行调整,使得全部障碍物点都在椭圆外
while inside_obs_points:
# 得到与椭圆距离最近的点
closest_obs_point = ellipse.closestPoint(inside_obs_points)
# 将最近点转到椭圆坐标系下
closest_obs_point = np.dot(np.transpose(rotation), closest_obs_point - ellipse.d_)
# 根据最近点,在椭圆长轴不变的情况下对短轴进行改变,使得,障碍物点在椭圆上
if Compare.small(closest_obs_point[0], axes[0]):
axes[1] = np.abs(closest_obs_point[1]) / np.sqrt(1 - (closest_obs_point[0] / axes[0]) ** 2)
# 更新椭圆
ellipse.C_ = np.dot(rotation, np.dot(np.array([[axes[0], 0], [0, axes[1]]]), np.transpose(rotation)))
# 更新椭圆内部障碍物
inside_obs_points = ellipse.insidePoints(inside_obs_points, include_bound=False)
return ellipse
# 进行多面体的构建
def findPolygon(self, ellipse: Ellipse, init_polygon: Polygon, obs_points: list[np.array]) -> Polygon:
# 多面体由多个超平面构成
polygon_planes = copy.deepcopy(init_polygon.hyper_planes_)
# 初始化范围超平面
remain_obs_points = obs_points
while remain_obs_points:
# 得到与椭圆最近障碍物
closest_point = ellipse.closestPoint(remain_obs_points)
# 计算该处的切平面的法向量
norm_vector = np.dot(np.linalg.inv(ellipse.C_), np.dot(np.linalg.inv(ellipse.C_), (closest_point - ellipse.d_)))
norm_vector = self.normalize(norm_vector)
# 构建平面
hyper_plane = Hyperplane(norm_vector, closest_point)
# 保存到多面体平面中
polygon_planes.append(hyper_plane)
# 去除切平面外部的障碍物
new_remain_obs_points = list()
for point in remain_obs_points:
if Compare.small(hyper_plane.signDist(point), 0):
new_remain_obs_points.append(point)
remain_obs_points = new_remain_obs_points
polygon = Polygon(polygon_planes)
return polygon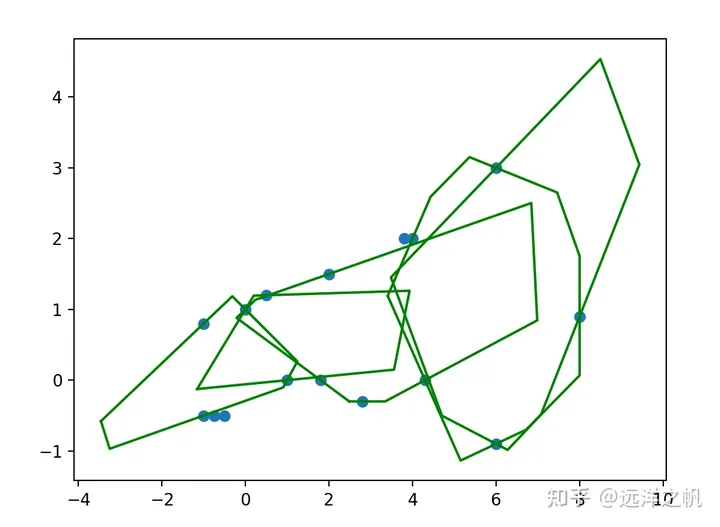
上面图是给定16个障碍物点,必经6个路径点后得到的凸包可行走廊,具体代码如下:
def main():
# 路径点
line_points = [np.array([-1.5, 0.0]), np.array([0.0, 0.8]), np.array([1.5, 0.3]), np.array([5, 0.6]), np.array([6, 1.2]), np.array([7.6, 2.2])]
# 障碍物点
obs_points = [
np.array([4, 2.0]),
np.array([6, 3.0]),
np.array([2, 1.5]),
np.array([0, 1]),
np.array([1, 0]),
np.array([1.8, 0]),
np.array([3.8, 2]),
np.array([0.5, 1.2]),
np.array([4.3, 0]),
np.array([8, 0.9]),
np.array([2.8, -0.3]),
np.array([6, -0.9]),
np.array([-0.5, -0.5]),
np.array([-0.75 ,-0.5]),
np.array([-1, -0.5]),
np.array([-1, 0.8])
]
convex_decomp = ConvexDecomp(2)
decomp_polygons = convex_decomp.decomp(line_points, obs_points, False)
#convex_decomp.decomp(line_points, obs_points,False)
plt.figure()
# 绘制障碍物点
plt.scatter([p[0] for p in obs_points], [p[1] for p in obs_points], marker="o")
# 绘制边界
for polygon in decomp_polygons:
verticals = polygon.getVerticals()
# 绘制多面体顶点
plt.plot([v[0] for v in verticals] + [verticals[0][0]], [v[1] for v in verticals] + [verticals[0][1]], color="green")
#plt.plot(x_samples, y_samples)
plt.show()带凸包走廊求解
带凸包走廊的光滑轨迹生成。前面已经求解得到了可行的凸包走廊,这部分可以做为硬约束作为最优化求解的不等式条件。要求的光滑路径和必须经过点的点,这部分可以把必须经过点作为等式约束,光滑路径可以通过代价函数来实现。这样就可以把带软硬约束的轨迹生成框架各种技能点都用上了。
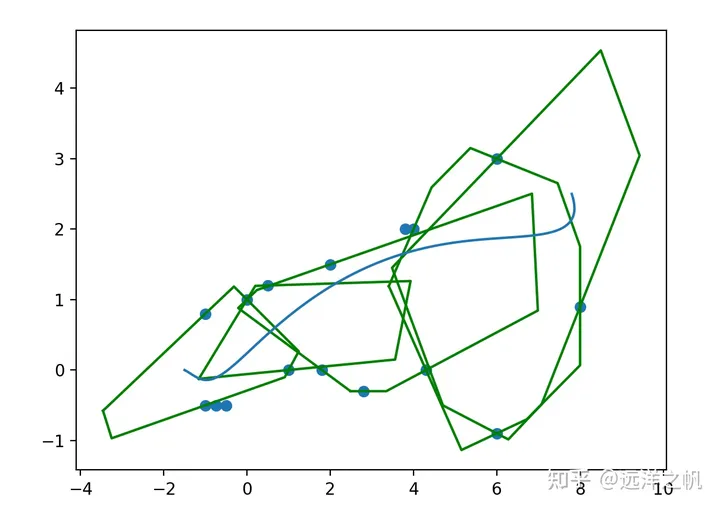
下面看具体代码实现:
# 进行优化
def optimize(self, start_state: np.array, end_state: np.array, line_points: list[np.array], polygons: list[Polygon]):
assert(len(line_points) == len(polygons) + 1)
# 得到分段数量
segment_num = len(polygons)
assert(segment_num >= 1)
# 计算初始时间分配
time_allocations = list()
for i in range(segment_num):
time_allocations.append(np.linalg.norm(line_points[i+1] - line_points[i]) / self.vel_max_)
# 进行优化迭代
max_inter = 10
cur_iter = 0
while cur_iter < max_inter:
# 进行轨迹优化
piece_wise_trajectory = self.optimizeIter(start_state, end_state, polygons, time_allocations, segment_num)
# 对优化轨迹进行时间调整,以保证轨迹满足运动上限约束
cur_iter += 1
# 计算每一段轨迹的最大速度,最大加速度,最大jerk
condition_fit = True
for n in range(segment_num):
# 得到最大速度,最大加速度,最大jerk
t_samples = np.linspace(0, time_allocations[n], 100)
v_max, a_max, j_max = self.vel_max_, self.acc_max_, self.jerk_max_
for t_sample in t_samples:
v_max = max(v_max, np.abs(piece_wise_trajectory.trajectory_segments_[n][0].derivative(t_sample)), np.abs(piece_wise_trajectory.trajectory_segments_[n][1].derivative(t_sample)))
a_max = max(a_max, np.abs(piece_wise_trajectory.trajectory_segments_[n][0].secondOrderDerivative(t_sample)), np.abs(piece_wise_trajectory.trajectory_segments_[n][1].secondOrderDerivative(t_sample)))
j_max = max(j_max, np.abs(piece_wise_trajectory.trajectory_segments_[n][0].thirdOrderDerivative(t_sample)), np.abs(piece_wise_trajectory.trajectory_segments_[n][1].thirdOrderDerivative(t_sample)))
# 判断是否满足约束条件
if Compare.large(v_max, self.vel_max_) or Compare.large(a_max, self.acc_max_) or Compare.large(j_max, self.jerk_max_):
ratio = max(1, v_max / self.vel_max_, (a_max / self.acc_max_)**0.5, (j_max / self.jerk_max_)**(1/3))
time_allocations[n] = ratio * time_allocations[n]
condition_fit = False
if condition_fit:
break
return piece_wise_trajectory
# 优化迭代
def optimizeIter(self, start_state: np.array, end_state: np.array, polygons: list[Polygon], time_allocations: list, segment_num):
# 构建目标函数 inter (jerk)^2
inte_jerk_square = np.array([
[720.0, -1800.0, 1200.0, 0.0, 0.0, -120.0],
[-1800.0, 4800.0, -3600.0, 0.0, 600.0, 0.0],
[1200.0, -3600.0, 3600.0, -1200.0, 0.0, 0.0],
[0.0, 0.0, -1200.0, 3600.0, -3600.0, 1200.0],
[0.0, 600.0, 0.0, -3600.0, 4800.0, -1800.0],
[-120.0, 0.0, 0.0, 1200.0, -1800.0, 720.0]
])
# 二次项系数
P = np.zeros((self.dim_ * segment_num * self.freedom_, self.dim_ * segment_num * self.freedom_))
for sigma in range(self.dim_):
for n in range(segment_num):
for i in range(self.freedom_):
for j in range(self.freedom_):
index_i = sigma * segment_num * self.freedom_ + n * self.freedom_ + i
index_j = sigma * segment_num * self.freedom_ + n * self.freedom_ + j
P[index_i][index_j] = inte_jerk_square[i][j] / (time_allocations[n] ** 5)
P = P * 2
P = sparse.csc_matrix(P)
# 一次项系数
q = np.zeros((self.dim_ * segment_num * self.freedom_,))
# 构建约束条件
equality_constraints_num = 5 * self.dim_ + 3 * (segment_num - 1) * self.dim_
inequality_constraints_num = 0
for polygon in polygons:
inequality_constraints_num += self.freedom_ * len(polygon.hyper_planes_)
A = np.zeros((equality_constraints_num + inequality_constraints_num, self.dim_ * segment_num * self.freedom_))
lb = -float("inf") * np.ones((equality_constraints_num + inequality_constraints_num,))
ub = float("inf") * np.ones((equality_constraints_num + inequality_constraints_num,))
# 构建等式约束条件(起点位置、速度、加速度;终点位置、速度;连接处的零、一、二阶导数)
# 起点x位置
A[0][0] = 1
lb[0] = start_state[0]
ub[0] = start_state[0]
# 起点y位置
A[1][segment_num * self.freedom_] = 1
lb[1] = start_state[1]
ub[1] = start_state[1]
# 起点x速度
A[2][0] = -5 / time_allocations[0]
A[2][1] = 5 / time_allocations[0]
lb[2] = start_state[2]
ub[2] = start_state[2]
# 起点y速度
A[3][segment_num * self.freedom_] = -5 / time_allocations[0]
A[3][segment_num * self.freedom_ + 1] = 5 / time_allocations[0]
lb[3] = start_state[3]
ub[3] = start_state[3]
# 起点x加速度
A[4][0] = 20 / time_allocations[0]**2
A[4][1] = -40 / time_allocations[0]**2
A[4][2] = 20 / time_allocations[0]**2
lb[4] = start_state[4]
ub[4] = start_state[4]
# 起点y加速度
A[5][segment_num * self.freedom_] = 20 / time_allocations[0]**2
A[5][segment_num * self.freedom_ + 1] = -40 / time_allocations[0]**2
A[5][segment_num * self.freedom_ + 2] = 20 / time_allocations[0]**2
lb[5] = start_state[5]
ub[5] = start_state[5]
# 终点x位置
A[6][segment_num * self.freedom_ - 1] = 1
lb[6] = end_state[0]
ub[6] = end_state[0]
# 终点y位置
A[7][self.dim_ * segment_num * self.freedom_ - 1] = 1
lb[7] = end_state[1]
ub[7] = end_state[1]
# 终点x速度
A[8][segment_num * self.freedom_ - 1] = 5 / time_allocations[-1]
A[8][segment_num * self.freedom_ - 2] = -5 / time_allocations[-1]
lb[8] = end_state[2]
ub[8] = end_state[2]
# 终点y速度
A[9][self.dim_ * segment_num * self.freedom_ - 1] = 5 / time_allocations[-1]
A[9][self.dim_ * segment_num * self.freedom_ - 2] = -5 / time_allocations[-1]
lb[9] = end_state[3]
ub[9] = end_state[3]
# 连接处的零阶导数相等
constraints_index = 10
for sigma in range(self.dim_):
for n in range(segment_num - 1):
A[constraints_index][sigma * segment_num * self.freedom_ + n * self.freedom_ + self.freedom_ - 1] = 1
A[constraints_index][sigma * segment_num * self.freedom_ + (n+1) * self.freedom_] = -1
lb[constraints_index] = 0
ub[constraints_index] = 0
constraints_index += 1
# 连接处的一阶导数相等
for sigma in range(self.dim_):
for n in range(segment_num - 1):
A[constraints_index][sigma * segment_num * self.freedom_ + n * self.freedom_ + self.freedom_ - 1] = 5 / time_allocations[n]
A[constraints_index][sigma * segment_num * self.freedom_ + n * self.freedom_ + self.freedom_ - 2] = -5 / time_allocations[n]
A[constraints_index][sigma * segment_num * self.freedom_ + (n+1) * self.freedom_] = 5 / time_allocations[n + 1]
A[constraints_index][sigma * segment_num * self.freedom_ + (n+1) * self.freedom_ + 1] = -5 / time_allocations[n + 1]
lb[constraints_index] = 0
ub[constraints_index] = 0
constraints_index += 1
# 连接处的二阶导数相等
for sigma in range(self.dim_):
for n in range(segment_num - 1):
A[constraints_index][sigma * segment_num * self.freedom_ + n * self.freedom_ + self.freedom_ - 1] = 20 / time_allocations[n]**2
A[constraints_index][sigma * segment_num * self.freedom_ + n * self.freedom_ + self.freedom_ - 2] = -40 / time_allocations[n]**2
A[constraints_index][sigma * segment_num * self.freedom_ + n * self.freedom_ + self.freedom_ - 3] = 20 / time_allocations[n]**2
A[constraints_index][sigma * segment_num * self.freedom_ + (n+1) * self.freedom_] = -20 / time_allocations[n + 1]**2
A[constraints_index][sigma * segment_num * self.freedom_ + (n+1) * self.freedom_ + 1] = 40 / time_allocations[n + 1]**2
A[constraints_index][sigma * segment_num * self.freedom_ + (n+1) * self.freedom_ + 2] = -20 / time_allocations[n + 1]**2
lb[constraints_index] = 0
ub[constraints_index] = 0
constraints_index += 1
# 构建不等式约束条件
for n in range(segment_num):
for k in range(self.freedom_):
for hyper_plane in polygons[n].hyper_planes_:
A[constraints_index][n * self.freedom_ + k] = hyper_plane.n_[0]
A[constraints_index][segment_num * self.freedom_ + n * self.freedom_ + k] = hyper_plane.n_[1]
ub[constraints_index] = np.dot(hyper_plane.n_, hyper_plane.d_)
constraints_index += 1
assert(constraints_index == equality_constraints_num + inequality_constraints_num)
A = sparse.csc_matrix(A)
# 进行qp求解
prob = osqp.OSQP()
prob.setup(P, q, A, lb, ub, warm_start=True)
res = prob.solve()
if res.info.status != "solved":
raise ValueError("OSQP did not solve the problem!")
# 根据参数进行轨迹解析
trajectory_x_params, trajectory_y_params = list(), list()
for n in range(segment_num):
trajectory_x_params.append(res.x[self.freedom_ * n: self.freedom_ * (n+1)])
trajectory_y_params.append(res.x[segment_num * self.freedom_ + self.freedom_ * n: segment_num * self.freedom_ + self.freedom_ * (n+1)])
piece_wise_trajectory = PieceWiseTrajectory(trajectory_x_params, trajectory_y_params, time_allocations)
return piece_wise_trajectory小结:
这篇文章介绍了带软硬约束的轨迹优化算法框架。第一部份介绍了软硬约束对应到最优求解问题数学上如何表示。第二部份介绍了贝赛尔曲线的代码实现,给出了具体的代码实现和讲解;并针对没有障碍物场景只给定waypoint点,生成光滑的Bezier轨迹的朴素求解代码实现。第三部份给出了带障碍物情况下如何做最优化求解,如何通过代价函数的方式来给轨迹施加推力让轨迹远离障碍物的代码实现。第四部分是一个综合性的例子,把软硬约束最优轨迹生成的求解框架做了一个综合呈现。详细的介绍了如何利用障碍物地图生成最大可行区域的凸包走廊,如何利用Bezier曲线的特性给定凸包两点生成路径一定在凸包中;以及如何利用代价行数来保证轨迹的光滑性、安全性,通过等式、不等式约束实现轨迹必须经过哪些点,某个点的运动状态如何。
这一系列的文章已经进入结尾的阶段,后面会简单介绍在碰到移动的物体时候单机器人如何处理;以及在多个机器人运行环境如何协同,最后会给出一个Motion Planning的综合实现例子讲解实际环境数据输入、前端规划、后端轨迹生成。至于定位和感知部分的内容后面可以根据情况而定是否在开一个新的系列来讲解介绍,对于更前沿的技术点会跟进论文做些文章分享。
最后本系列文章的代码在以下git链接,这部分代码相对零碎主要是配合文章理论来讲的,里面很多片段直接来源于网络整合。后面这可项目会持续维护,把项目代码(应该是c++实现,更体系)、整合进来,根据需要在看看有没必要整合出一个库。
投稿作者为『自动驾驶之心知识星球』特邀嘉宾,欢迎加入交流!
① 全网独家视频课程
BEV感知、毫米波雷达视觉融合、多传感器标定、多传感器融合、多模态3D目标检测、车道线检测、轨迹预测、在线高精地图、世界模型、点云3D目标检测、目标跟踪、Occupancy、cuda与TensorRT模型部署、大模型与自动驾驶、Nerf、语义分割、自动驾驶仿真、传感器部署、决策规划、轨迹预测等多个方向学习视频(扫码即可学习)
 视频官网:www.zdjszx.com
视频官网:www.zdjszx.com
② 国内首个自动驾驶学习社区
近2400人的交流社区,涉及30+自动驾驶技术栈学习路线,想要了解更多自动驾驶感知(2D检测、分割、2D/3D车道线、BEV感知、3D目标检测、Occupancy、多传感器融合、多传感器标定、目标跟踪、光流估计)、自动驾驶定位建图(SLAM、高精地图、局部在线地图)、自动驾驶规划控制/轨迹预测等领域技术方案、AI模型部署落地实战、行业动态、岗位发布,欢迎扫描下方二维码,加入自动驾驶之心知识星球,这是一个真正有干货的地方,与领域大佬交流入门、学习、工作、跳槽上的各类难题,日常分享论文+代码+视频,期待交流!

③【自动驾驶之心】技术交流群
自动驾驶之心是首个自动驾驶开发者社区,聚焦目标检测、语义分割、全景分割、实例分割、关键点检测、车道线、目标跟踪、3D目标检测、BEV感知、多模态感知、Occupancy、多传感器融合、transformer、大模型、点云处理、端到端自动驾驶、SLAM、光流估计、深度估计、轨迹预测、高精地图、NeRF、规划控制、模型部署落地、自动驾驶仿真测试、产品经理、硬件配置、AI求职交流等方向。扫码添加汽车人助理微信邀请入群,备注:学校/公司+方向+昵称(快速入群方式)

④【自动驾驶之心】平台矩阵,欢迎联系我们!






















 5168
5168











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








