几何光学学习笔记（16）- 4.5 光楔

4.5 光楔

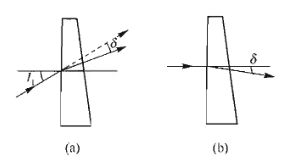
折射角 a 很小的棱镜称为光楔，它在光学仪器中有很多用途。折射棱镜的公式用于光楔时可以简化。光线的入射角具有一定大小时，因α 角很小，可近似地认为是平行平板。

$$\delta =\alpha (\frac{ncos{I}_1^{\prime }}{cos{I}_1}-1)$$

当$I_1^{\prime }和I_1$很小时，上式中的余弦值可以用1代替。
$$\delta =\alpha (n-1)$$
此式表明，当光线垂直或近于垂直射入光棋时，如图(b)所示，其所产生的偏角仅取决于光楔的折射角和折射率的大小。

1.共轴双光楔

在光学仪器中，常把两块相同的光棋组合在一起相对转动，可以产生不同大小的偏向角，如图所示。两光模间有一微小空气间隙，相邻工作面平行，并可绕其公共法线相对转动。图 (a) 表示两光楔主截面平行，两折射角朝向一方，将产生最大的总偏向角(为两光模产生偏向角之和)。图(b) 为两光楔相对转动 180°，两主截面仍平行，但折射角方向相反，显然，这个系统相当于一个平行平板，偏向角为零。图（c） 表示两光楔相对转动 180°，产生与图(a)相反的总偏向角。

可以利用两个光模之间间隙的变化，以改变出射光线的平移量
$$\Delta y=\Delta zd=\Delta z(n-1)\alpha$$

2.偏轴双光楔

当两主截面不平行或相对转动任意角习2j时，则组合光模的总偏角为：
$$\delta =2\alpha (n-1)cosj$$
这种双光棋可以把光线的小偏向角转换成为两个光模的相对转角。因此，在光学仪器中常用它来补偿和测量小角度误差，即把小角度误差转换成为两个光模间的很大的相对转角，从而可以读出小角度误差。

共轴双光楔间有一微小空气间隙，如果用于对激光束偏转，因激光束能量集中，会产生多次反射和折射(类似于腔体作用)，使光学系统中产生大量杂散光，为此可采用偏轴双光楔结构。