螺线的工程学应用

等距螺线（阿基米德螺线，等速螺线）

• 等距螺线是一种特殊的曲线形状，具有一些有趣的性质和应用。
  • 极坐标表达：等距螺线可以用极坐标表达：等距螺线的参数方程为 r(θ) = a + bθ
  • 几何性质：等距螺线呈现出逐渐扩大或逐渐收缩的螺旋形状。
    • 它们在数学上是无限延伸的曲线，但通常只绘制一部分。等距螺线具有平坦的曲率
  • 应用领域：等距螺线在工程和科学领域中有广泛应用。
    • 设计螺旋桨和螺旋翼，以实现最佳的气动性能
    • 描述行星和彗星的轨道

import matplotlib.pyplot as plt
import numpy as np

def Equidistant_spiral(a, b, num_points=5000, n=5):
    theta = np.linspace(0, 2 * np.pi * n, num_points)
    r = a + b * theta

    x = r * np.cos(theta)
    y = r * np.sin(theta)

    plt.plot(x, y)
    plt.axis("equal")
    plt.title("Equidistant Spiral")
    plt.pause(0.01)


a = 1  
b = 5  
num_points = 1000 

Equidistant_spiral(a, b, num_points)

a = 1 b = 5 

 

a = 1 b = -5  

 

 

a = 1 b = -0.05  

 

 a = 1 b = -0.005  

 

费马螺线

• 费马螺线
  • 极坐标表达：费马螺线也可以用极坐标表达。其参数方程为 r(θ) = a * θ^0.5，其中 r 是距离中心点的距离，θ 是极角，a 是常数。费马螺线的极径与极角之间的关系是反余弦函数，这使得螺线上的每个点到中心点的距离与极角之间存在特定的关系。
  • 几何性质：费马螺线呈现出逐渐收敛的螺旋形状。与等距螺线不同，费马螺线的曲率是变化的，从而产生了类似于金螺旋线的形态。
  • 应用领域：费马螺线在工程和科学领域中也有广泛应用。
    • 光学设计中，费马螺线被用于设计透镜表面，以实现特定的光学效果。
    • 地理学中用于描述地球表面上的估计等高线。

 

 

等角螺线

• 等角螺线
  • 极坐标表达：等角螺线可以用极坐标表达。其参数方程为 r(θ) = a * exp(bθ)
  • 几何性质：等角螺线呈现出逐渐扩大或逐渐收缩的螺旋形状，类似于费马螺线
  • 应用领域：
    • 机械设计中，等角螺线可以用于设计螺纹连接、齿轮传动等，以实现最佳的机械性能。
    • 地理学和地质学中，等角螺线可以用于描述地壳变形和地震活动等现象。

a = 1  b = -1 

a = 1  b = 1 

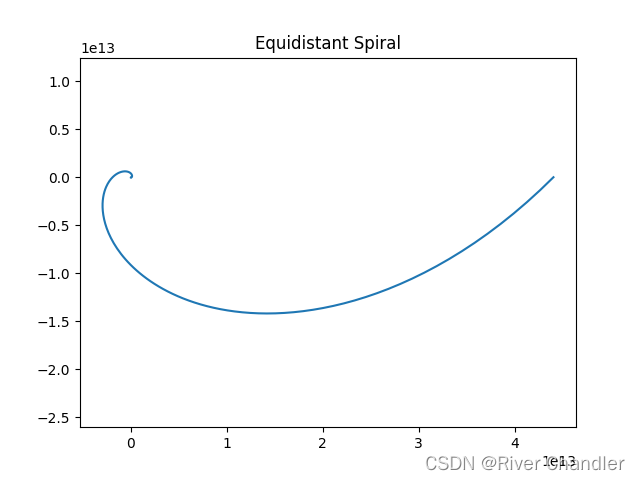
•  注意看坐标

a = 1  b = -10 

a = 1  b = 0.1 

欧拉螺线

• 详见代码

L=2 

 

L=20

双曲螺线

连锁螺线

斐波那契螺线