阿基米德螺旋线如何等距取点？

动感光波是如何练就的

已于 2022-10-17 16:30:39 修改

阅读量7.3k

点赞数 24

文章标签： matlab

于 2022-10-14 19:49:20 首次发布

本文链接：https://blog.csdn.net/z1622675271/article/details/127278495

版权

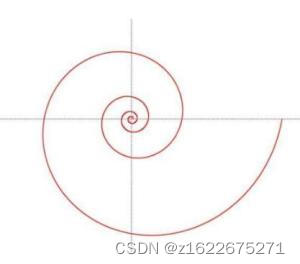
注，程序中的a,b并不对应公式，有空再改~

极坐标下：

$r=a+b\theta$

如果想要等距取点我们首先想到螺旋线的长度公式，求出长度与 $\theta$ 的关系即可等距取点。

计算过程可见知乎《ρ=a+bθ阿基米德螺线弧长怎么计算？》

---公式相当复杂，解出 $\theta$ 非常困难。

如果在其物理意义上进行操作，是否可行？

$r=a+b\theta$

可写为时间函数：

$\theta =\omega t$ ，可见角速度 $\omega$ 为常数，为匀角速度运动。但是半径 $r$ 是线性函数，随着角度的增大而增大。这样线速度可以看作是加速度运动。

clear all
t=[0:0.001:1];
w=5*pi;
b=0;
a=1;
zeta=w*t;
r=a*zeta+b;
x=r.*cos(zeta);
y=r.*sin(zeta);
figure
scatter(x,y)
%plot(x,y)

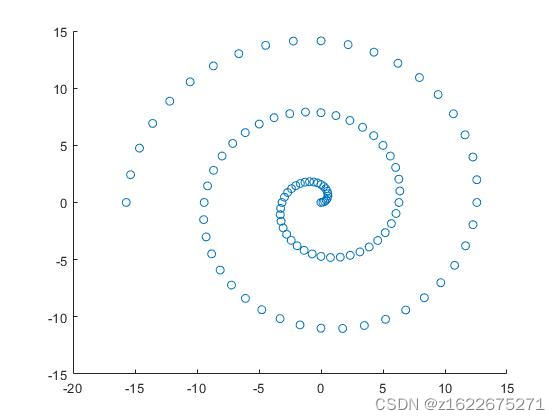
上图为等时间间隔打点图，显而易见，中间非常密集，沿曲线渐变稀疏，如何实现等间距打点，就是实现阿基米德螺旋曲线的等距取点问题。

思路：1.按照弧长公式，解出 $t$ 与 $l$ 的关系，按 $nl$ 取 $t$ 值；

2.看作直线加速度运动，求出路程 $l$ 和 $t$ 的关系。

$v=\omega r=\omega \left ( a+b\omega t \right )=\omega a+b\omega ^{^{2}}t$

$l=\omega at+\frac{1}{2}b\omega ^{2}t^{2}$

解 $t$ 与 $nl$ 的关系，

clear all
n0=40;
n=[1:1:n0];
w=2*pi;
l0=pi/20;
b=0.005;
a=0.1-b;
t=(sqrt(b^2+2*a.*n*l0)-b)/(a*w);
zeta=w*t;

r=a*zeta+b;
x=r.*cos(zeta);
y=r.*sin(zeta);
figure
scatter(x,y)

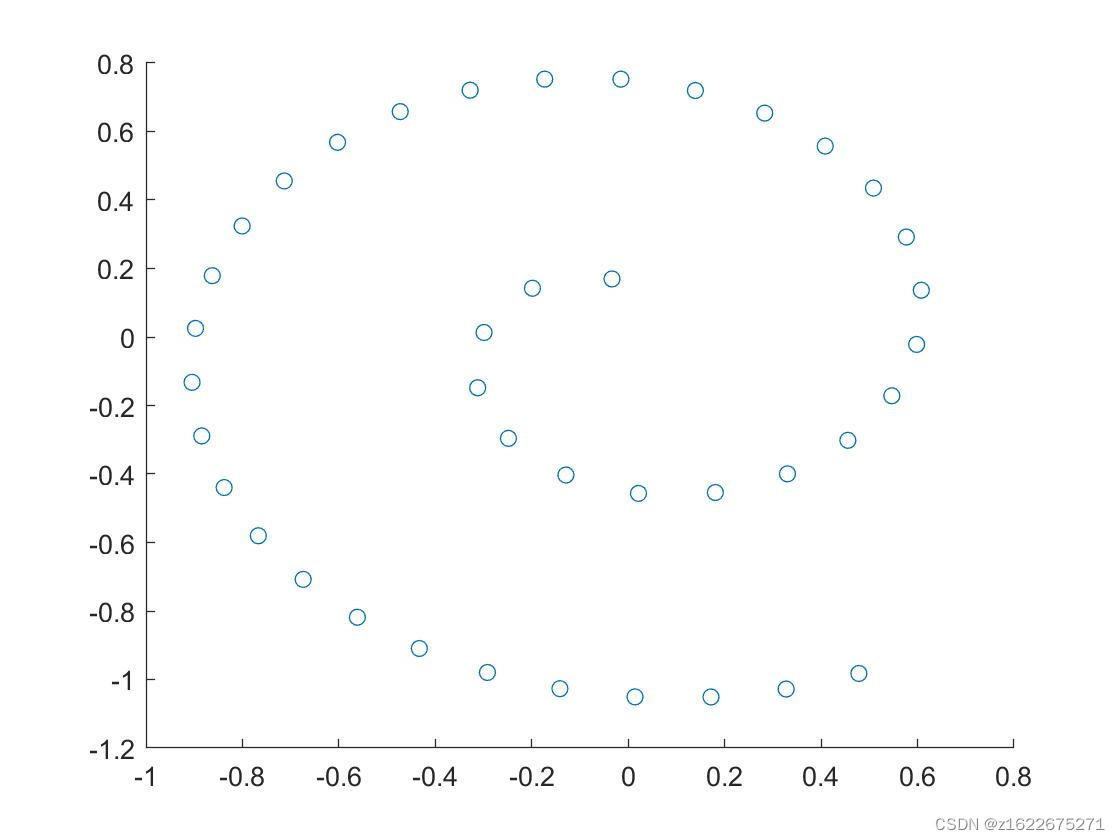
此时，可见是准等距打点图像，当我们放大半径可见并不严格等距，原因是？? ?

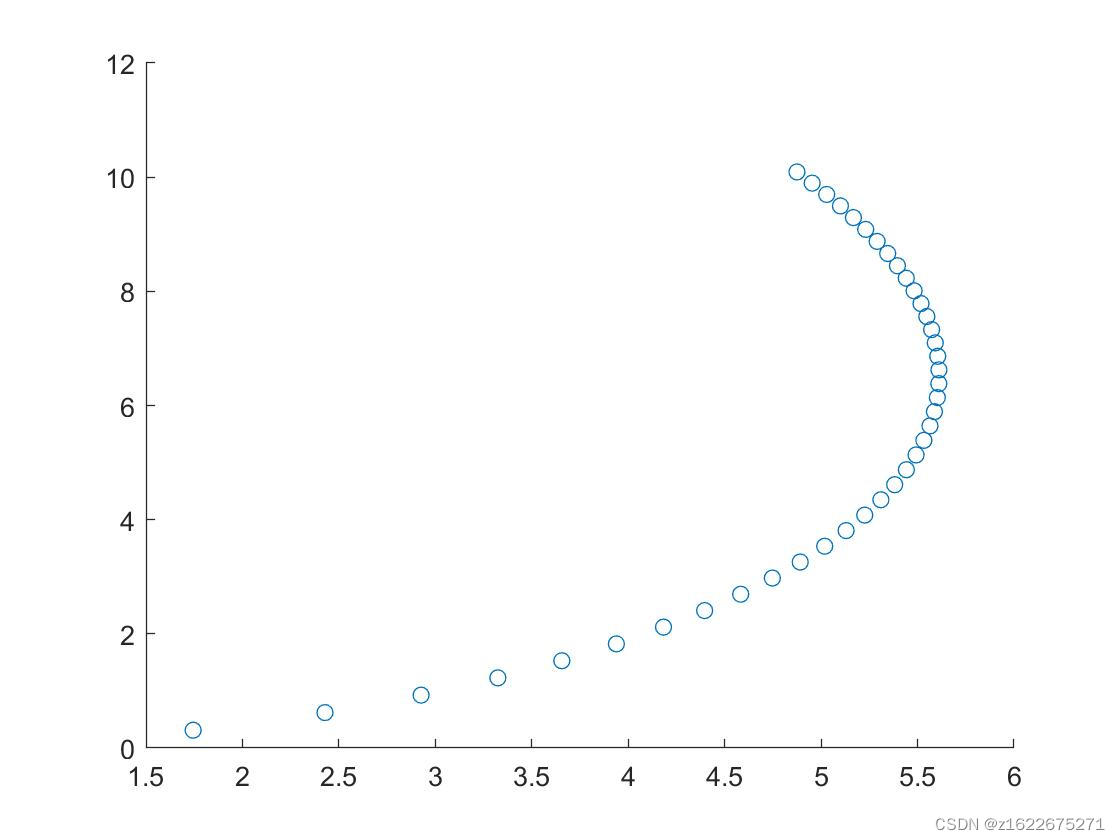
线速度与角速度的转换关系是圆周运动的条件下，也就是线速度方向正交于半径，但是在螺旋线中，线速度并不正交于半径，尤其当半径增大时，正交性更差，所以误差变大。目前来讲这只是一个粗略等距取点。对于直接求解阿基米德螺旋线弧长与角度的关系不太理想，如果大家有比较好的思想欢迎留言~