一、目标函数:利润最大化


二、利润最大化必要条件
1、内点解
(1)单要素情况:

(2)双要素情况:

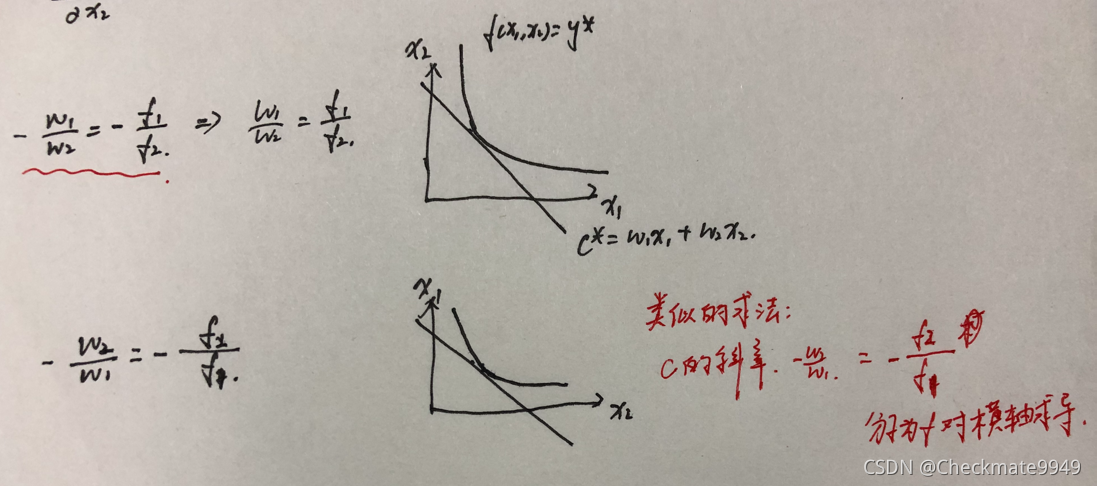
2、角点解:
即存在投入水平为0的要素。即X>=0。我们结合该约束条件构建拉格朗日函数:

可知,当投入生产要素为0时,其边际产出价值: 必然小于该要素价格
。
注意:这里的p为产品价格,为边际产量,两者相乘为边际价值。
三、要素需求函数的性质
1、厂商要素需求:
; 厂商产品供给:
。
产品供给为要素需求的函数;要素需求为要素价格、产品价格的函数。
2、要素需求函数 是要素价格的减函数
是要素价格的减函数
(1)利润最大化的一二阶必要条件
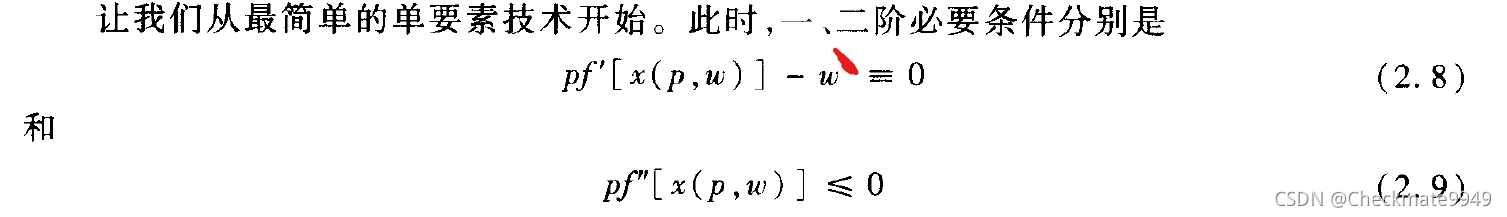
(2)一阶必要条件等式对要素价格 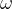 求导,得
求导,得

又已知二阶必要条件等式![]()
因此,要素需求函数对要素价格的导数小于0,即要素需求是要素价格的减函数。
3、要素需求函数 为产品价格的增函数
为产品价格的增函数
(1)同样根据利润最大化的一二阶必要条件:
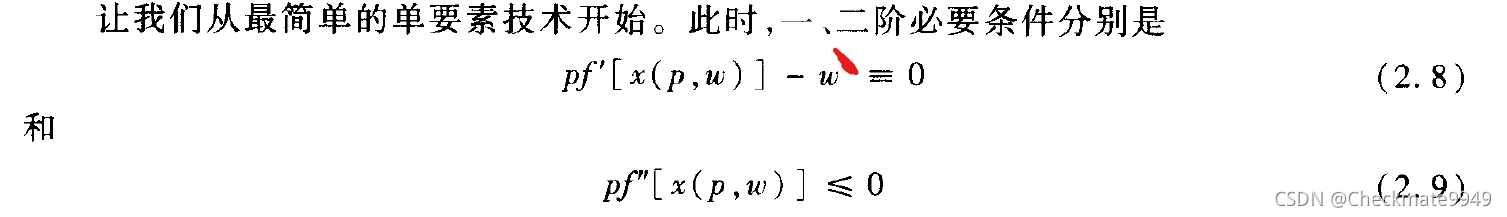
(2)等式(2.8)对产品价格p求导:

整理得,
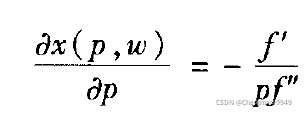
又根据一阶必要条件![]() 知
知
根据二阶必要条件知 ,得

可知要素需求函数为产品价格的增函数。
4、双要素情况:要素需求为其价格的减函数
(1)根据利润函数对产品价格求一阶导:

(2)对要素1价格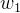 求一阶偏导 :
求一阶偏导 :

(3)对要素2价格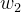 求一阶偏导 :
求一阶偏导 :


(4)写成矩阵形式:

求逆,得

已知利润最大化的二阶必要条件为:生产函数的海赛矩阵为半负定的

因此得等式左侧矩阵为半负定的,其主对角线元素为负值,即:

得要素需求为其价格的减函数。
5、双要素情况:要素价格的交叉效应对称
又知生产函数的海赛矩阵为对称矩阵,即f12=f21,因此左侧矩阵同样为对称矩阵,得:

因此,要素i需求量对要素j价格的弹性 等于 要素j需求量对要素i价格的弹性,即要素价格的交叉效应对称。
四、利润函数
将厂商所能达到的最大利润定义为其利润函数

1、利润函数的性质
(1)是产品价格p的增函数,是每一要素价格
的减函数;
(2)是
的一次齐次函数:
![]() ;
;
(3) 是
的凸函数。
2、证明: 是产品价格p的增函数
是产品价格p的增函数
(1)设要素需求函数,设
(2)根据利润函数定义:
知
(3)因为为利润最大化的解,因此
大于任何利润函数,注意只改变X(p,w)的值
得
(4)又根据知,
,
即
(5)最终得,,证明
为产品价格p的增函数。
3、证明:  是每一要素价格
是每一要素价格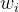 的减函数
的减函数
(1)同理设
得
因为为利润最大化的解,因此其利润函数
大于任何利润,仍然只改变X(p,w)的值
得
即,证明
是每一要素价格
的减函数。
4、证明:利润函数为一次齐次函数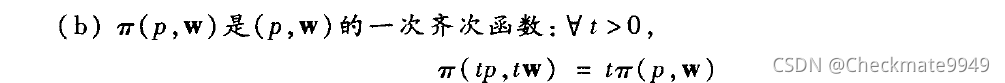
设为利润最大化问题的解,因此其大于所有利润函数
![]()
两边同乘t,得
![]()
因此X(p,w)为下述最大化问题的解:

写出PI(tp, tw)的函数,将t提取出来,即得证。

5、证明:利润函数为(p,w)的凸函数











 本文探讨了经济学中的利润最大化问题,包括单要素和双要素情况下的必要条件。解释了内点解和角点解的概念,并阐述了要素需求函数的性质,如是要素价格的减函数和产品价格的增函数。此外,还讨论了利润函数的性质,证明了它是产品价格的增函数和要素价格的减函数,并且是一次齐次函数和凸函数。
本文探讨了经济学中的利润最大化问题,包括单要素和双要素情况下的必要条件。解释了内点解和角点解的概念,并阐述了要素需求函数的性质,如是要素价格的减函数和产品价格的增函数。此外,还讨论了利润函数的性质,证明了它是产品价格的增函数和要素价格的减函数,并且是一次齐次函数和凸函数。

















 1134
1134

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








