我把N-Gram关键的几句话贴出来(对别人帖子的一些修改):
该模型基于这样一种假设,第n个词的出现只与前面N-1个词相关,而与其它任何词都不相关,整句的概率就是各个词出现概率的乘积。这些概率可以通过直接从语料中统计N个词同时出现的次数得到。常用的是二元的Bi-Gram和三元的Tri-Gram。
在介绍N-gram模型之前,让我们先来做个香农游戏(Shannon Game)。我们给定一个词,然后猜测下一个词是什么。当我说“艳照门”这个词时,你想到下一个词是什么呢?我想大家很有可能会想到“陈冠希”,基本上不会有人会想到“陈志杰”吧。N-gram模型的主要思想就是这样的。
对于一个句子T,我们怎么算它出现的概率呢?假设T是由词序列W1,W2,W3,…Wn组成的,那么P(T)=P(W1W2W3Wn)=P(W1)P(W2|W1)P(W3|W1W2)…P(Wn|W1W2…Wn-1)
补充知识:
但是这种方法存在两个致命的缺陷:一个缺陷是参数空间过大,不可能实用化;另外一个缺陷是数据稀疏严重。
为了解决这个问题,我们引入了马尔科夫假设:一个词的出现仅仅依赖于它前面出现的有限的一个或者几个词。
如果一个词的出现仅依赖于它前面出现的一个词,那么我们就称之为bigram。即
P(T) = P(W1W2W3…Wn)=P(W1)P(W2|W1)P(W3|W1W2)…P(Wn|W1W2…Wn-1)
≈P(W1)P(W2|W1)P(W3|W2)…P(Wn|Wn-1)
如果一个词的出现仅依赖于它前面出现的两个词,那么我们就称之为trigram。
在实践中用的最多的就是bigram和trigram了,而且效果很不错。高于四元的用的很少,因为训练它需要更庞大的语料,而且数据稀疏严重,时间复杂度高,精度却提高的不多。
那么我们怎么得到P(Wn|W1W2…Wn-1)呢?一种简单的估计方法就是最大似然估计(Maximum Likelihood Estimate)了。即P(Wn|W1W2…Wn-1) =(C(W1 W2…Wn))/(C(W1 W2…Wn-1))
剩下的工作就是在训练语料库中数数儿了,即统计序列C(W1 W2…Wn) 出现的次数和C(W1 W2…Wn-1)出现的次数。
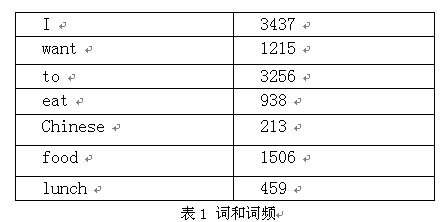
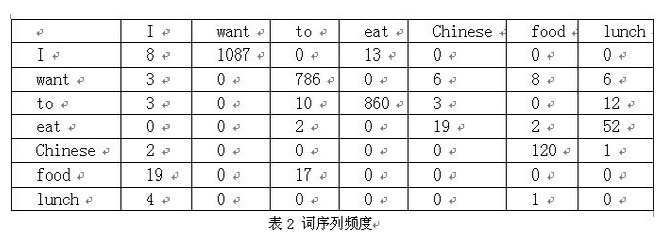
下面我们用bigram举个例子。假设语料库总词数为13,748
P(I want to eat Chinese food)
=P(I)*P(want|I)*P(to|want)*P(eat|to)*P(Chinese|eat)*P(food|Chinese)
=0.25*1087/3437*786/1215*860/3256*19/938*120/213
=0.000154171
这里还有一个问题要说,那就是数据稀疏问题了,假设词表中有20000个词,如果是bigram那么可能的N-gram就有400000000个,如果是trigram,那么可能的N-gram就有8000000000000个!那么对于其中的很多词对的组合,在语料库中都没有出现,根据最大似然估计得到的概率将会是0,这会造成很大的麻烦,在算句子的概率时一旦其中的某项为0,那么整个句子的概率就会为0,最后的结果是,我们的模型只能算可怜兮兮的几个句子,而大部分的句子算得的概率是0. 因此,我们要进行数据平滑(data Smoothing),数据平滑的目的有两个:一个是使所有的N-gram概率之和为1,使所有的N-gram概率都不为0。
转自:http://blog.sina.com.cn/s/blog_4b2ddd15010151th.html#commonComment
http://blog.csdn.net/lengyuhong/article/details/6022053









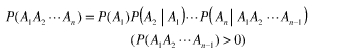














 3726
3726

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








