趣味三角——第7章——圆的内外旋轮线

ComputerInBook

于 2023-02-06 01:08:07 发布

阅读量1.5k

点赞数

分类专栏：数学与应用数学文章标签：三角学三角圆的内外旋轮线内摆线外摆线

本文链接：https://blog.csdn.net/ComputerInBook/article/details/128895366

版权

数学与应用数学专栏收录该内容

129 篇文章

订阅专栏

本文探讨了圆外旋轮线和圆内旋轮线的历史、数学原理及应用，包括Spirograph玩具如何展示这些曲线。此外，介绍了MariaAgnesi及其对“箕舌线”（又称“女巫”曲线）的研究，展示了18世纪女性在数学领域的贡献。文章还涵盖了这些曲线的参数方程、性质以及在天文学和机械工程中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

第7章圆外旋轮线和圆内旋轮线

(Epicycloids and Hypocycloids)

1. 圆外旋轮线和圆内旋轮线的发展历程

2. Maria Agnesi和她的“箕舌线”(Maria Agnesi and Her “Witch”)(又名：Maria Agnesi 和她的 “女巫”)

1. 圆外旋轮线和圆内旋轮线的发展历程

The epicycle theory [of the motion of the planets], in the

definite form given by Ptolemy, stands out as the most

mature product of ancient astronomy.

([行星运动的]周转圆理论,由Ptolemy以明确的形式给出，作为古代天文学的成熟产品脱颖而出。)

译注：epicycle词义为“small circle moving on or around another circle (在另一个圆上或围绕另一个向前转动的一个更小的圆)”。

——Anton Pannekoek，<< A History of Astronomy>>(天文学史)

在20 世纪 70 年代，一款有趣的(intriguing)益智玩具(educational toy)出现在市场上并迅速走红：呼吸运动记录计(spirograph)。它由一组大小不一的塑料制成的小轮子组成，轮子的轮辋(wǎng，旧式车轮周围的框子)上有齿，两个大环的内外轮辋上都有齿(图 39)。小孔在距中心不同距离处穿孔(perforated)在每个轮子上。您将其中一个环钉在一张纸上，将一个轮子与其接触以便齿啮(niè)合，然后将一支笔插入其中一个孔中。当你绕着圆环移动轮子时，纸上会画出一条曲线——假如齿轮沿着环的内部移动，就形成了一条圆内旋轮线

(hypocycloid)，而假如齿轮沿着环的外部移动，则形成了一条圆外旋轮线(epicycloid)(这两个名称来自古希腊词前缀,“hypo-”=“under(在……之下)”， “epi-”=“over(在……之上)”)。曲线的确切形状取决于环的半径(radii，radius的复数)和齿轮(每个都以其轮辋上的牙齿数量表示)；更确切地说，是取决于半径的比率(ratio)。

-----------------------------图39 spirograph(呼吸运动记录计)---------------------------------

让我们来求得内旋轮线的参数方程，即求得半径为r的圆上的一点，当它沿着半径为R的固定圆的内沿滚动时的轨迹(图 40)。

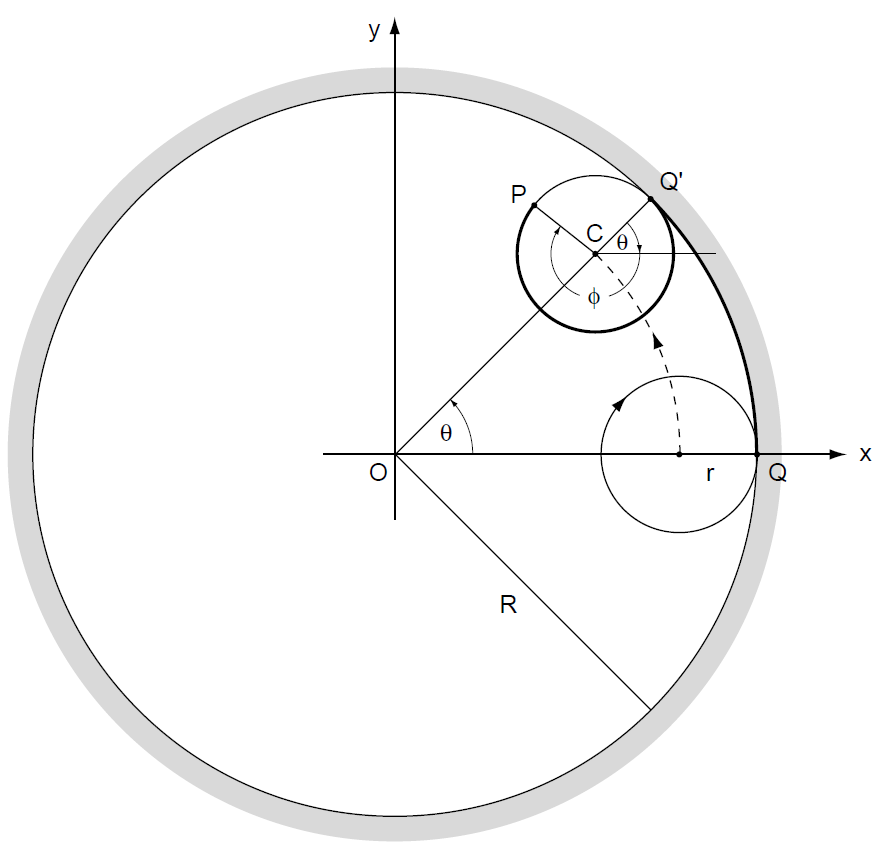
-----------------------------图40 产生内旋轮线-------------------------------

令O和C分别为固定圆和滚动圆的圆心，P为滚动圆上的任意一点。当滚动圆沿顺时针方向转过角Φ时，C沿逆时针方向画出了大小为θ弧度的圆心角。假设P点从与Q点相接触的位置开始滚动，我们选择一个坐标系统，其中原点位于O且x轴指向Q点方向。P相对于C点的坐标是(r cos Φ，-r sin Φ)(第二个坐标中的减号是因为Φ是按顺时针度量的)，而C相对于O的坐标是((R-r) cos θ，(R-r) sin θ)。因此，P相对于O点的坐标是

x = (R-r) cos θ + r cos Φ ，y = (R-r) sin θ - r sin Φ--------------------(1)

但是角θ和Φ并不是独立的：随着移动的进行，固定圆上与移动圆接触的弧(弧QQ’和Q’P，见图40)一定等长。这两段弧长分别是Rθ和r(θ + Φ)，因此，我们有Rθ = r(θ + Φ)。根据这种关系，用θ来表达Φ，我们得到Φ = ，因此，方程(1)

就变成

x = (R-r) cos θ + r cos [(R-r)/ r] θ，

y = (R-r) sin θ - r sin [(R-r)/ r] θ--------------------(2)

因此，方程(2)便是圆内旋轮线的参数方程，其中，θ是参数(假如滚动圆以固定的角速率滚动，θ将与从起点开始计时的运动时间成正比)。曲线的一般形状取决于R/ r的比率。假如比率是分数m/n值的最小项，则这个曲线将具m个尖点(cusps)(拐角(corners))，并且在将车轮绕内缘移动n次后将完全描绘出曲线。如果 R/ r 是非比率数(即，不能表示成两个整数的分数形式)，则曲线永远不会闭合，尽管多次绕过边缘几近闭合。

对于R/ r的某些值，导致的曲线可能在某种程序上令人诧异。例如，当R/ r = 2时，方程(2)就成了

x = r cos θ + r cos θ = 2r cos θ，

y = r sin θ - r sin θ = 0--------------------(3)

事实上，在任何时间点y = 0都意味着P点仅沿着x轴移动，沿着环的内直径来来回回地绘制轨迹。这样我们就可以用两个半径比为2:1的圆来画一条直线段！在19世纪，将圆周运动转换为直线运动，或者反之，这类问题对于蒸汽机(steam engines)的设计至关重要：活塞(piston)的往复运动(to-and-fro)必须转换为轮子的旋转。 2:1圆内旋轮线是提出的众多解决方案之一。

甚至更有趣的是R/ r= 4这种情况,对于这种情况，方程(2)就成了

x = 3 r cos θ + r cos3 θ，

y = 3 r sin θ - r sin3 θ 。--------------------(4)

为了得到曲线的矩形方程——忽略掉P点的x坐标和y坐标的方程——我们必须消除这两个方程之间的参数θ。一般情况下，这样做可能会要求使用某些冗长的代数操作，并且导致的方程——即便最终可以达成预期——也是非常复杂。但是，在这个案例中，一对三角恒等式可以帮助我们达成目的——即，恒等式

$cos^{3}\theta =(3cos\theta+cos3\theta)/4$

和

$sin^{3}\theta=(3sin\theta+sin3\theta)/4$ [1]。则，方程(4)成了

$x=4 rcos^{3}\theta , y=4 rsin^{3}\theta---------------------(5)$

对每个方程取立方根，对结果进行平方，相加，最终得到

$x^{\frac{2}{3}}+y^{\frac{2}{3}} = (4r)^{\frac{2}{3}}=R^{\frac{2}{3}}$

按照方程(5)描述的内旋轮线称为“星形线(astroid)”；它具有星形(star)(因此得名)的形状，其四个角分别位于θ = 0°，90°，180°，270°位置。星形线具有某些显著特征。例如，它的所有正切线在x轴之间截取(intercept)相同长度的x轴,这个长度为R。而发过来，如果允许一条固定长度为R的线段其位于x轴和y轴的端点占据所有可能的位置，所有的线段就构成了一个封闭的形状——这些曲线的每一个切线合在一起——就构成了一个星形线(见图41)。

----------------------图41 由切线构成的星形线----------------------------

因此，靠在墙上的梯子其占据所有可能位置构成的区域形成星形。令人惊奇的是，这个星形也是椭圆(ellipses)簇 $x^{2}/y^{2}+y^{2}/(R-a)^{2} = 1$ 的封闭区域，其长半轴和短半轴之后为R(图42)。[2]

----------------------图42 由切线椭圆构成的星形线----------------------------

如此巧合的是，星形的直角方程(方程5)使得计算这条曲线的各种度量属性变得特别容易。例如，使用求曲线弧长的微积分公式，可以证明星形体的周长为6R(令人惊呀的是，尽管圆圈参与了星形的生成，但它的周长并不取决于常量π) 。星形封闭区域的面积是 $3\pi R^{2}/8$ ，或者八分之三的(three-eighths)固定圆面积。[3]

在1725年，Daniel Bernoulli(1700–1782), 即受人尊敬的(venerable)伯努利数学家家族成员之一，他发现了被称为“二重生成定理(double generation theorem)”的圆内旋轮线的一个美丽性质。半径为r的圆在半径为R的固定圆的内侧滚动产生与半径为R − r的圆在同一个固定圆内滚动相同的圆内旋轮线。假如我们将前一个圆内旋轮线记为[R ，r]，后一个记为[R ，R − r],则定理说的意思就是[R ，r] = [R ，R − r]。注意两个滚动圆相对于固定圆是互补的：它们的直径之和等于固定圆的直径(图43)。

----------------------图43 Bernoulli的二重生成定理----------------------------

为了证明这个定理，让我们利用等式(1)中的特殊斜对称性(skew-symmetry)。在这些方程中，用r’ 替换掉R – r，我们得到

x = r’cos θ + (R –r’)cos Φ ，y = r’sin θ - (R –r’)sin Φ 。

但是，参数θ和Φ通过等式(R – r)θ = rΦ关联在一起。我们使用Φ表达θ，我们有

θ = rΦ/ (R – r) = [(R –r’)/ r’ ] Φ。因此，方程(1)化为

x = r’cos [(R –r’)/ r’ ] Φ + (R –r’)cos Φ

y = r’sin [(R –r’)/ r’ ] Φ - (R –r’)sin Φ--------------------(6)

对于方程(6)，除了r’代替r之外，与方程(2)惊人地相似。事实上，我们可以交换每个方程各项的次序，使其与方程(2)形式相同:

x = (R –r’)cos Φ + r’ cos [(R –r’)/ r’]Φ

y = -(R –r’)sin Φ + r’ sin [(R –r’)/ r’]Φ

r’替代r，θ和Φ互换位置之后，以上方程中的第一个与(2)中的第一个完全相同。但是第二个方程仍然有一个令人烦恼的(bothersome)符号错位：我们希望第一项为正，第二项为负。这时，还是这对三角恒等式可以帮到我们。即奇偶恒等式cos(-Φ) = cos Φ和sin (-Φ) = sin Φ。让我们再次替换参数，用Ψ = -Φ消掉Φ ；这使得第一个方程的项不受影响，但交换了第二个方程中的项的符号：

x = (R –r’)cos Ψ + r’ cos [(R –r’)/ r’] Ψ

y = (R –r’)sin Ψ - r’ sin [(R –r’)/ r’] Ψ--------------------(7)

这与方程(2)形式完全相同。这就完成了证明。[5]

作为这个定理的结果，我们可以有，例如，[4r, r] = [4r, 3r]，或者，等价形式，[R, R /4] = [R, 3R/4]——说明，由方程(5)描述的星形线，也可以通过半径为3R/4的圆沿着半径为R的固定圆内部滚动生成。

圆外旋轮线的参数方程——半径为r的圆上的一点沿着半径为R的固定圆的外部滚动划出来的曲线——可以类比于圆内旋轮线(方程(2))：

x = (R+r) cos θ - r cos [(R+r)/ r] θ，

y = (R+r) sin θ - r sin [(R+r)/ r] θ 。--------------------(8)

最明显的，R+r替换(R-r不言自明,但也要注意x方程第二项中的减号；这是因为滚动圆的旋转与其中心的运动现在是“同”向的。

与圆内旋轮线一样，圆外旋轮线的形状取决于R/r的比率。对于R/r = 1，方程(8)化简为x = r(2 cos θ - cos 2 θ)，y = r(2sin θ - sin 2θ),因此，产生的曲线是心型心脏型曲线(cardioid)(图44)。它有一个单一的尖头(cusp)，位于P与固定圆接触的位置。其周长为16R面积为 $6\pi R^{2}$ 。[7]

----------------------图44 心脏型曲线(Cardioid)----------------------------

必须考虑另一种情况：半径为r的圆在半径为R的固定圆的外侧滚动并在内部接触它(图45)。[7] 这种情况类似于圆内旋轮线，只是固定和滚动的作用不同，圆圈是相反的。这种情况下的参数方程是

x = rcosΦ –(r - R)cosθ ，y = rsinΦ –(r - R)sinθ，

(注意，现在r > R)，其中，θ和Φ通过等式(r-R)θ = rΦ关联起来。根据Φ来表达θ并使用替换式r’ = r-R，这些方程化为

x = (R + r’ )cosΦ –r’cos[(R+ r’ )/ r’ ] Φ ，

y = (R + r’ )sinΦ –r’sin[(R+ r’ )/ r’ ] Φ 。--------------------(9)

------------图45 一个大圆圈在一个小圆圈的外面滚动，大圆内部接触小圆外部-----

对于圆外旋轮线而言，除却r’替代r和Φ代替θ之外，方程(8)和方程(9)等价。因此，随后的(ensuing)曲线与通过半径为r’ =r - R沿着半径为R的固定圆在外部接触滚动而产生的圆外旋轮线等效。相反，后者形成的圆外旋轮线等价于通过半径为r = R+ r’ 的圆沿着半径为R的固定圆通过外部接触滚动而产生的曲线等价。这就是圆外旋轮线的二重生成定理。如果我们引入符号{}和()分别表示“外部(external)”和“内部(internal)”圆外旋轮线，则定理讲的就是{ R,r} = (R,R + r)(我们去掉了r上的上标符号('))。因此，对于心脏形曲线我们有{ R, R } = (R,2R)。

圆外旋轮线的研究可以追溯到古希腊人，古希腊人用它们来解释一种令人费解的天体现象：从地球上看，行星偶尔会逆行(retrograde motion)。在它沿黄道带(zodiac)的大部分运动中，一颗行星从西向东移动；但偶尔这颗行星似乎会停滞不前，然后将其轨道(course)反转为从东向西运动，然后再次停止并恢复其正常轨道。对于具有审美头脑的古希腊人来说，唯一可以想象的天体绕地球运行的曲线是圆——完美的象征。但是圆不允许逆行运动，所以古希腊人假设行星实际上沿着一个小圆运动，即周转圆(epicycle)，其中心沿着主圆移动，即均轮(deferent)(图46)。但当甚至这个模型也不能完全解释所观察到的行星运动时，他们添加了越来越多的本轮，直到系统被本轮所累以至于变得笨拙。尽管如此，该系统确实至少近似地描述了观测事实，并且是第一个真正用数学来解释天体运动的尝试。

--------图46 行星本轮(Planetary epicycles) 来自 1798 年的版画(作者的收藏)。-----

直到1543年哥白尼(Copernicus)发表他的日心说(heliocentric theory)时，本轮的必要性才消失：随着地球绕太阳公转，逆行运动立即被解释为从运动的地球上看行星的相对运动的结果。因此，当丹麦天文学家奥劳斯·罗默(Olaus Roemer，1644-1710 年)作为第一个确定光速而闻名的人在1674年着手研究摆线曲线时，它与天体无关，而是与一个更普通的问题有关——工作的机械齿轮(mechanical gears)。

使用当今的计算机和图形计算器，即使是最复杂的曲线也可以在几秒钟内生成。但就在一两代人之前，这样的任务还完全依赖于机械设备；事实上，许多巧妙的工具被发明来绘制特定类型的曲线(图47和48)[8]。这些设备通常涉及高度复杂的机制，但看着齿轮移动并缓慢地描绘出预期的曲线，还是有一定的吸引力；从字面上看，您可以看到机器在工作。随着机械世界让位给电子时代，效率以亲密为代价取得了胜利。

-----图47 椭圆仪(Ellipsograph)。来自 Keuffel&Esser的产品目录，1928 年-----

图48 椭圆仪(Ellipsograph)。来自F. W. Devoe的测量和数学仪器目录，大约1900。

看着齿轮转动并慢慢沿着预期的曲线运动，有一种迷人的感觉；从字面上看，您可以看到机器在工作。随着机械世界让位给电子时代，效率以亲密为代价取得了胜利。[7]

注释和资料来源：

1. 这些等式可以通过分别使用三角公式

$cos3\theta =4cos^{3}\theta-3cos\theta$

和

$sin3\theta=3sin\theta-4sin^{3}\theta$

求解 $cos^{3}\theta$ 和 $sin^{3}\theta$ 从而得解。

2. 要看到这种效果，考虑长度为R且其两个端点沿x轴和y轴自由移动的线段上的一点P(x, y)(图49)。

------------------图49 随着θ的变化, P点描述了矩形的弧------------------

假如P将线段划分成分别为a和b两部分，我们有，cos θ = x/a，sin θ = y/b。平方之后再相加，得到 $x^{2}/a^{2}+y^{2}/b^{2} = 1$ ，这是一个半长轴为a和R- a的椭圆方程。因此，当允许线段占据所有可能的位置时，点P将绘制椭圆(这是图47中所示的椭圆绘图机的基础)。对于沿着线段的不同位置的P(即，当a/b的比率取不同的值时，a + b仍然是常量)将绘制不同的椭圆,常见的封闭区域是椭圆

$x^{2/3}+y^{2/3} = R^{2/3}$ 。

3. 关于星形线的其它性质，参见Robert C. Yates的著作<<Curves and their Properties>>(曲线及其性质)(1952初版;Reston,Virginia:National Council of Teachers of Mathematics(数学教师委员会), 1974重印)

4. 请注意，我们可以自由地将一个参数替换为另一个参数，前提是新参数导致x和y覆盖与旧参数相同的取值范围。在我们的例子中，这是由正弦和余弦函数的周期性确保的。

5. 双重生成定理也可以通过几何方式证明；参见Robert C. Yates的著作<<Curves and their Properties>>(曲线及其性质)的第81-82页。

6. 熟悉的心脏型极坐标方程 ρ = r(1- cos θ)成尖点位于原点时成立(这里表示正x轴和线 OP之间的极角；这不要与出现在方程8中的角θ混淆)。有关心型曲线请参见Yates <<Curves and their Properties>>的第4-7页。

7. 我要感谢威斯康星大学欧克莱尔分校的(the University of Wisconsin–Eau Claire) Robert Langer提醒我注意这个案例。

8. 参见H. Martyn Cundy和A. P. Rollett合著的<<Mathematical Models>>(数学模型) (London: 牛津大学出版社, 1961版)第2章和第5章。

9. 芝加哥科学与工业博物馆的参观者会发现一个有趣的机械齿轮陈列，这些机械齿轮谦虚地隐藏在其中一个楼梯上，几乎被博物馆宽敞大厅中的大型展品所掩盖。通过用手移动一个小曲柄，您可以激活齿轮并观看随后的运动——一个过去时代的无声提醒。

2. Maria Agnesi和她的“箕舌线”(Maria Agnesi and Her “Witch”)(又名：Maria Agnesi 和她的 “女巫”)

即使在今天，女性仅占美国数学家总数的10% 左右；[1] 在世界范围内，她们的人数要少得多。但在过去的几代人中，社会偏见使得女性几乎不可能从事科学事业，而本世纪女性数学家的总数用两只手都能数过来。我想到了三个名字：俄罗斯的Sonia Kovalevsky (1850–1891)、Emmy Noether(1882–1935)，她出生于德国但移居美国，以及意大利的 Maria Agnesi。[2]

Maria Gaetana Agnesi(发音为“Anyesi”)于 1718 年出生于米兰，她一生的大部分时间都在那里度过。[3] 她的父亲Pietro是Bologna大学富有的数学教授，鼓励她学习科学。为了让她继续接受教育，他在他们家创办了一种“文化沙龙(cultural salon)”，客人来自欧洲各地，其中许多是各个领域的学者。在这些客人面前，年轻的Maria展示了她的才智，展示了关于各种主题的论文，然后在辩论中为他们辩护。科目包括逻辑学、哲学、力学、化学、植物学、动物学和矿物学。在中场休息期间，她的妹妹Maria Teresa是一位作曲家和大键琴演奏家，她用她的音乐来娱乐客人。这一幕让人想起Leopold Mozart在Salzburg富裕的沙龙中炫耀年轻的Amadeus的音乐才华，Mozart的妹妹南Nannerl在背景中演奏。 Maria Gaetana 还精通多种语言：五岁时她已经能说流利的法语，九岁时她被翻译成拉丁语并发表了一篇倡导女性接受高等教育的长篇演讲。很快她就掌握了希腊语、德语、西班牙语和希伯来语，并会用客人的母语为她的论文答辩。她后来收集了其中的190篇论文，并将它们发表在一本书<<Proportiones philosophicae>>(1738年)中；不幸的是，她的数学思想没有包含在这部作品中。

到Agnesi十四岁时，她已经能够解决解析几何和物理学中的难题。十七岁时，她开始对 Guillaume L'Hospital 的作品 Trait´e analytique des coniques 进行批判性评论；不幸的是，这篇评论从未发表过。大约在那个时候，她已经受够了公开展示自己的才华。她退出社交生活，全身心投入到数学中。在接下来的十年里，她写下了她的主要著作<<Instituzioni analytice ad uso della gioventu italiana>>(针对意大利年轻人使用的分析机构)。这部作品于1748年出版，分为两卷，第一卷涉及代数，第二卷涉及分析(即无限过程)。她的目标是对这些当时已知的主题进行完整和综合的介绍(我们必须记住，在18世纪中叶，微积分仍处于发展阶段，新的程序和定理不断被添加到它的现有核心)。Agnesi用意大利语而不是当时的学术语言拉丁语写了这本书，目的是让尽可能多的“年轻意大利人”能够接触到它。

Instituzioni使Agnesi立即得到认可，并被翻译成多种语言。 John Colson(卒于1760 年)是剑桥大学的卢卡斯教授，他在1736年发表了牛顿通量法和无限级数(他的微积分)的第一个完整阐述，并将Agnesi的书翻译成英文。当他已经年事已高时，专门为这项任务学习意大利语，“以便英国青年和意大利青年都能从中受益”。他的译本于1801年在伦敦出版。

为表彰她的成就，教皇Benedict十四世于1750年任命Agnesi为Bologna大学的数学教授。但她从未真正在那里教过书，只是将自己的职位视为一种荣誉职位。1750年她父亲去世后，她逐渐退出科学活动，将余生投入宗教和社会工作。她还抚养了她父亲的21个孩子(来自三段婚姻)并指导他们的教育，同时帮助她教区的穷人。1799年，她在米兰去世，享年81岁。

具有讽刺意味的是，今天人们记住Agnesi的名字主要是因为她研究过但不是第一个研究的曲线：“Agnesi的箕舌线(the witch of Agnesi)”。考虑半径为a圆心位于(0,a)的圆(图50)。

--------------------------------------------图50箕舌线------------------------

一条穿过(0,0)点的直线与圆上的A点相交并继续延伸直到水平线y = 2a相交与B点。绘制一条穿过点A和过点B的垂直线的相交与P点的水平线。箕舌线是P的轨迹，因为直线 OA占据了所有可能的位置。

根据OA和y轴之间的角度θ，最容易找到箕矢线方程。令P点的坐标为(x, y)，从图50我们可以看出，∠OAC = 90°，OC是圆的一条直径；因此，在直角三角形∠OAC中，我们有 OA = OC cos θ = 2a cos θ。令R和S分别为相对x轴从A到B步长，则在直角三角形OBS中, 我们有OS = x = BC tanθ = 2a tanθ ，在直角三角形OAR中我们有 $AR = y = OAcos\theta = 2acos^{2} \theta$ 。

因此，箕舌线的参数方程为

$x = 2a tan\theta ,y = 2acos^{2}\theta-------------------(1)$

为了求得其直角方程，我们必须消除(1)中两个等式之间的θ 。使用恒等式

$1+tan^{2}\theta=1/cos^{2}\theta$ 根据x来表达y，我们得到

$y=\frac{8a^{3}}{x^{2}+4a^{2}}-----------------(2)$

从方程(2)可以得出几个结论：第一，随着x->±∞，y->0 ，说明x轴是箕舍线的水平渐近线(asymptote)。第二，用微积分的知识，你可以证明箕舌线与渐近线之间的面积为 $4\pi a^{2}$ 或者所产生的圆的面积的4倍。[4] 它还可以表明——直接从方程(2)或者从参数方程(1)——箕实线具有两个曲折点(曲线改变凹性的位置)位于±π/6。计算有点冗长但简单明了，我们在此略去。

如前所述，“箕舌线”并非起源于Agnesi； Pierre Fermat (1601–1665) 已经知道它，Pisa大学的数学教授路Luigi Guido Grandi(1671–1742)将其命名为“versiera”(来自拉丁语“vertere”，词义为“to turn(转变)”)。然而，巧合的是，一个发音相似的意大利语单词“aversiera”的意思是女魔鬼(devil)或魔鬼的妻子。根据D. J. Struik 的说法，“英国的一些才子曾将其译为‘女巫’，这个愚蠢的双关语至今仍被精心保留在我们的大多数英语教科书中。”[6] 因此，Grandi的“versiera”成为了“Agnesi的女巫”。这条很少出现在应用程序中的特殊曲线为何让数学家感兴趣了这么久，这有点令人费解。[7] 它奇怪的名字可能与此有关，或者也许是Agnesi让这条曲线广为人知的作用。

注释和资料来源：

1. 该图基于美国数学学会的年度AMS-IMS-MAA调查，1993年秋季。

2. 关于女科学家的一个很好的来源是Marilyn Bailey Ogilvie，<<Women in Science—Antiquity through the Nineteenth Century: A Biographical Dictionary with Annotated Bibliography>>(科学领域中的女性——多古代到十九世纪：带注释书目的传记词典)(剑桥, Mass.:MIT 出版社, 1988出版)以及<<Women of Mathematics: A Bibliographical Sourcebook >>(数学领域中的女性:原始文献书目)( Louise S. Grinstein和Paul J. Campbell版) (New York: Greenwood Press, 1987)。

3. 本章中的传记详细信息改编自DSB(Dictionary of Scientific Biography)第一卷第75-77页。另见Ogilvie <<Women in Science>>第26-28页。

4. 以下来自公式

$2\int_{0}^{\infty }ydx = 8a^{2}tan^{-1}(x/2a)|_{0}^{\infty }=4\pi a^{2}$

其中 $tan^{-1}$

是反正切(或者反三角)函数；我们使用了箕舌线关于y轴对称的事实。

5. 箕舌线的另外一些性质可以在Robert C. Yates的著作<<Curves and their Properties>>(曲线及其性质)(Reston, Va.: National Council of Teachers of Mathematics(全国数学教师委员会), 1974)第237-238页中获得。

6. <<A Source Book in Mathematics: 1200–1800>>(数学原始资料)(剑桥, Mass.: Harvard大学出版社会, 1969年版)第178-181页。根据这个资料的记载，第一个在这个意义上使用词“witch”的人可能是B. Williamson，他在他著作<< Integral Calculus>>(微积分学)(1875年)中首次使用该词。Yates(在“曲线”一书的第237页)对“witch”这个名称的使用有一另一个不同的演进版本：“似乎Agnesi将古意大单词‘versorio’(这个名称已经被Grandi赋予了这个曲线)(词义为‘在任意方向上自由移动’)与‘versiera’(词义为‘goblin(小妖精)’, ‘bugaboo(妖怪)’, ‘Devil’s wife(魔鬼的妻子)’，等等)搞混淆了。”

7. 这条曲线在概率论中表现为柯西分布

$f(x) = \frac{1}{\pi (1+x^{2})}$ ，