频域稳定性分析

起因：在学习自控原理的过程中一直对频域分析有些疑问。有些人说通过伯德图就可以看出系统是否稳定。但是我不知道如何观察，于是又重新学习了一下频域分析。在此简单做一下总结。
首先明白两个要素：
1.频域稳定性分析是在稳态过程中，也就是说只有进入稳态后我们才关心系统的频率响应。
2.系统稳定的充分必要条件是，闭环传递函数在S域的右半平面没有极点。
因此根据要素二我们可以很轻松的判定系统是否稳定。
如果我们的输入信号只有阶跃信号那么我们也就不用讨论系统的频率响应，但是在实际生活中我们避免不了有一些正弦信号输入到我们的系统中。
频域稳定性判据主要有两个，分别是：奈奎斯特稳定性判据和对数稳定性判据。他们本宗同源。
我们先看奈奎斯特稳定性判据
理论基础：DR_CAN
首先我有一个疑问，奈奎斯特稳定性判据为什么是频域稳定性判据？他和频域有什么关系？
要回答这个问题我们首先要了解一下频域响应
很好，我已经了解了，那么进行下一步
这一步很重要，我们先看一个开环系统的幅相特性曲线，如图一所示。

问：在极坐标图下的这个蓝色曲线怎么来的呢？
答：就是 ω 从0-> ∞ 变化得来的。这个也就是我们用MATLAB nyquist()命令画出来的图
问：那这和系统的稳定有什么关系呢？
答：那关系可太大了，只要上面的图不过（-1，j0）点 并且逆时针包围（-1，j0）的圈数R等于开环传递函数的正实部极点数P，系统就是稳定的。
换人话说就也就是P=R系统就稳定，否则不稳定。并且有约束方程
其中Z就是闭环传递函数有半平面的极点个数。
你想想，右半平面都有极点了还能稳定吗？
问：为什么呢？为什么呢？为什么Z=其中Z就是闭环传递函数有半平面的极点个数？
为什么不过（-1，j0）点 …系统就是稳定的？
答：要回答这个问题，我们就要知道柯西幅角原理。此处我是讲不明白的，想具体了解请移步DR_CAN的频道。
虽然幅角原理讲不明白，但是我知道，在S域的右半平面是不能右极点的。只要右半平面有极点，那么系统就是不稳定的。
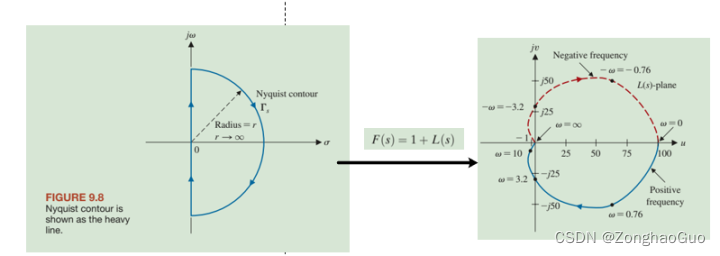
因此，我画个大圆（半个），通过F(S)的映射就能得到幅相特性曲线，
如果右侧图片算出来Z=1.就说明，左侧图片的蓝色圈圈内含有1个极点，
如果右侧图片算出来Z=2.就说明，左侧图片的蓝色圈圈内含有2个极点，
因此通过看右侧的图（开环传递函数）就能知道闭环传递函数是否稳定。
​

那么接下就是本文的最大问题。
问：那我直接写出来闭环传递函数多好,岂不是能更快的知道闭环传递函数是否有右侧极点？
答：是的，如果你直接写出来闭环传递函数是可以直接判定闭环系统是否稳定的。但是，遗憾的是，有些系统内部构造你无法精确建模，因此无法写出来。但是通过输入输出数据，可以很轻松的得到右侧的幅相特性曲线，因此，通过幅相特性曲线，就能轻松的判定闭环系统的稳定性。
问：那如果我们不能精确建模，那岂不是F(s)也写不出来？
答：是的，我们连F(S)也不知道。
问：如果连F（s）都不知道的话，我们如何确定p（闭环传递函数右半平面极点）的个数。
答： 如果一个无源系统，也就是没有外部输入的系统，它的开环传递函数一般是没有右半平面极点的，也就说 P=0。所以通过R值就可以确定Z值，进而判定系统的稳定性。