TWSVM

DaMeng999

已于 2022-04-28 19:18:43 修改

阅读量1k

点赞数 2

分类专栏： twsvm 文章标签：支持向量机机器学习分类

于 2022-04-28 15:43:38 首次发布

本文链接：https://blog.csdn.net/DaMeng999/article/details/124468189

版权

twsvm 专栏收录该内容

3 篇文章 0 订阅

订阅专栏

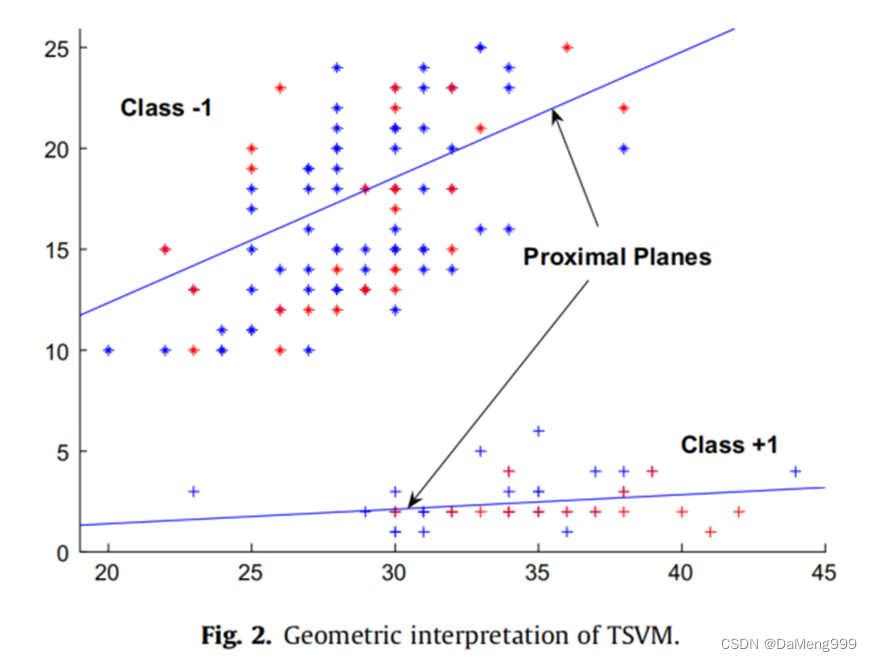
与传统的 SVM 相比，TWSVM 是求解一对非平行的超平面，其中一个超平面离正样本点更近，另一个超平面离负样本点更近；它的模型和 SVM 模型对比结果如下：

1. 原始最优化问题

TWSVM 分类器是求解如下一对 QPP 方程：

1.1 符号说明

$c_1 , c_2 > 0$ ，是人为调整的超参数；

$A \in \mathbb{R}^{m_1\times n}$ ， $m_1$ 是正样本的数目， $n$ 是样本的维数，矩阵 $A$ 意味着所有的正样本点；

$B \in \mathbb{R}^{m_2\times n}$ ， $m_2$ 是正样本的数目， $n$ 是样本的维数，矩阵 $B$ 意味着所有的负样本点；

$w_1, w_2 \in \mathbb{R}^{n\times 1}$ 是两个超平面的法向量；

$b_1, b_2$ 是两个超平面的常量；

$e_1\in\mathbb{R}^{m_1\times1}, e_2\in\mathbb{R}^{m_2\times1}$ 是全为 1 的向量；

$q$ 是松弛变量；

1.2 公式说明

在这里以第一个公式为例子，说明该公式的含义：

1.2.1

$\min _{w_1, b_1} \frac{1}{2}(Aw_1 + e_1b_1)^T(Aw_1 + e_1b_1)+c_1e_2^Tq$

这个最小化公式的第一项是所有正样本点到第一个超平面的距离的平方和，第二项是误差项；整个公示的含义是最小化所有正确分类样本点到这个超平面的距离的同时使误分类点的误差最小。它的矩阵形式如下所示：

$\min_{w_1,b_1} \frac{1}{2}\begin{bmatrix} X_1^{a}\cdot w_1+b1\\ X_2^{a}\cdot w_1 + b1\\ \vdots \\ X_{m_1}^a\cdot w_1 + b1 \end{bmatrix}^T\begin{bmatrix} X_1^{a}\cdot w_1+b1\\ X_2^{a}\cdot w_1 + b1\\ \vdots \\ X_{m_1}^a\cdot w_1 + b1 \end{bmatrix}+c_1\begin{bmatrix} 1\\ 1\\ \vdots \\ 1 \end{bmatrix}^T \begin{bmatrix} q_1\\ q_2\\ \vdots \\ q_{m_2} \end{bmatrix}$

展开后的公式如下所示：

$\min_{w_1,b_1}\frac{1}{2}\sum_{i=1}^{m_1}\left \| X_i^a\cdot w_1 + b_1 \right \|_2^2+c_1\sum_{i=1}^{m_2}q_i$

1.2.2

$s.t. -(Bw_1+e_2b_1)+q\geqslant e_2$

$q\geqslant 0$

这个不等式约束的含义是，要求负样本点到第一个超平面的距离不严格小于 1，并且允许有一定的误差，允许部分负样本点到第一个超平面的距离可以小于 1 。它的举证形式如下所示：

$-\begin{bmatrix} X_1^b\cdot w_1+b_1\\ X_2^b\cdot w_1+b_1\\ \vdots \\ X_{m_2}^b\cdot w_1+b_1 \end{bmatrix} + \begin{bmatrix} q_1\\ q_2\\ \vdots \\ q_{m_2} \end{bmatrix} \geqslant \begin{bmatrix} 1\\ 1\\ \vdots \\ 1 \end{bmatrix}$

2. 构造对偶问题求解

TWSVM 的原始最优化问题是一对凸二次规划问题，可以通过引入拉格朗日乘子构造拉格朗日函数求解，这里以第一个公式为例，构造得到的拉格朗日函数如下所示：

$\begin{align*} L(w_1,b_1,q,\alpha ,\beta)&= \frac{1}{2}(Aw_1+e_1b_1)^T(Aw_1+e1b_1)+c_1e_2^Tq\\ &-\alpha ^T(-(Bw_1+e_2b_1)+q-e_2)-\beta ^Tq \end{align*}$

这里引入拉格朗日乘子 $\alpha ,\beta \geqslant 0$ ，以向量表示。将矩阵展开得到的公式如下所示：

$\begin{align*} L &= \frac{1}{2}\sum_{i=1}^{m_1}\left \| X_i^a\cdot w_1 + b_1 \right \|_2^2+c_1\sum_{i=1}^{m_2}q_i\\ &+\sum_{i=1}^{m_2}\alpha _i(X_i^b\cdot w_1+b_1+1-q_i)-\sum_{i=1}^{m_2}\beta_iq_i \end{align*}$

然后可以转化为对拉格朗日函数求极大极小问题，即 $\max_{\alpha, \beta}\min_{w_1,b_1,q}L$

2.1 求极小

2.1.1

在本小节求对 $w_1$ 的偏导：

$\begin{align*} \frac{\partial L}{\partial w_1} &= \frac{\partial [\frac{1}{2}\sum_{i=1}^{m_1}\left \| X_i^a\cdot w_1 + b_1 \right \|_2^2+\sum_{i=1}^{m_2}\alpha_iX_i^b\cdot w_1]}{\partial w_1}\\ &=\frac{1}{2} \frac{\partial \sum_{i=1}^{m_1}[(X_i^a\cdot w_1)^T(X_i^a\cdot w_1)+b_1((X_i^a\cdot w_1)T+X_i^a\cdot w_1)]}{\partial w_1}+\sum_{i=1}^{m_2}\alpha_iX_i^b\\ &= \sum_{i=1}^{m_1}X_i^a\cdot (X_i^a\cdot w_1+b_1)+\sum_{i=1}^{m_2}\alpha_iX_i^b=0 \end{align*}$

其矩阵表达如下所示：

$A^T(Aw_1+e_1b_1)+B^T\alpha=0$

2.1.2

然后对 $b_1$ 求偏导：

$\begin{align*} \frac{\partial L}{\partial b_1} &= \frac{1}{2}\frac{\partial \sum_{i=1}^{m_1}(X_i^a\cdot w_1 + b_1)^T(X_i^a\cdot w_1 + b_1)}{\partial b_1}+\frac{\partial b_1\sum_{i+1}^{m_2}\alpha_i}{\partial b_1}\\ &= \frac{1}{2}\frac{\partial \sum_{i=1}^{m_1}[b_1((X_i^a\cdot w_1)^T+X_i^a\cdot w_1)+b_1^2]}{\partial b_1}\\ &= \sum_{i=1}^{m_1}X_i^a\cdot w_1 + b_1+\sum_{i=1}^{m_2}\alpha_i =0\end{align*}$

其矩阵表示如下：

$e_1^T(Aw_1+e_1b_1)+e_2^T\alpha=0$

2.1.3

最后对 q 求偏导：

$\begin{align*} \frac{\partial L}{\partial q_i} &= \frac{\partial (c_1\sum_{i=1}^{m_2}q_i-\sum_{i=1}^{m_2}\alpha_iq_i-\sum_{i=1}^{m_2}\beta_iq_i)}{\partial q_i}\\ &= c_1-\alpha_i-\beta_i=0 \end{align*}$

其矩阵表示如下：

$c_1e_2-\alpha-\beta=0$

2.2 KKT 条件

由条件 3 和 7 可知：

$0\leqslant \alpha_i \leqslant c_1, \: i=1,2,...,m_2$

结合条件 1 和 2 可以得到：

$\begin{bmatrix} A^T\\ e_1^T \end{bmatrix} \begin{bmatrix} A & e_1 \end{bmatrix} \begin{bmatrix} w_1\\ b_1 \end{bmatrix} + \begin{bmatrix} B^T\\ e_2^T \end{bmatrix} \alpha=0$

定义：

$H=\begin{bmatrix} A & e_1 \end{bmatrix} ,\: G=\begin{bmatrix} B & e_2 \end{bmatrix} ,\: u=\begin{bmatrix} w_1\\ b_1 \end{bmatrix}$

则有：

$H^THu+G^T\alpha=0$

于是解得极小值：

$u=-(H^TH)^{-1}G^T\alpha$

为增强泛化能力，可以引入正则化项：

$u=-(H^TH+\epsilon I)^{-1}G^T\alpha$

2.3 求极大

2.4 对偶问题

解得最终的对偶问题解如下：

$\left\{\begin{matrix} \max & \alpha^Te_2-\frac{1}{2}\alpha^TG(H^TH)^{-1}G^T\alpha\\ s.t.& 0\leqslant \alpha\leqslant c_1 \end{matrix}\right.$

$\left\{\begin{matrix} \max & \gamma^Te_1-\frac{1}{2}\gamma^TP(Q^TQ)^{-1}P^T\gamma\\ s.t.& 0\leqslant \gamma\leqslant c_2 \end{matrix}\right.$

DaMeng999

关注

2
点赞
踩
16

收藏

觉得还不错? 一键收藏
0
评论
TWSVM

与传统的 SVM 相比，TWSVM 是求解一对非平行的超平面，其中一个超平面离正样本点更近，另一个超平面离负样本点更近；它的模型和 SVM 模型对比结果如下：1. 原始最优化问题TWSVM 分类器是求解如下一对 QPP 方程：1.1 符号说明，是人为调整的超参数；，是正样本的数目，是样本的维数，矩阵意味着所有的正样本点；，是正样本的数目，是样本的维数，矩阵意味着所有的负样本点；是两个超平面的法向量；是两个超平面的常量；是...
复制链接

扫一扫