维基百科
点击打开链接
首先看一下维基百科的介绍
散列表(Hash table,也叫哈希表),是根据键(Key)而直接访问在内存存储位置的数据结构。也就是说,它通过计算一个关于键值的函数,将所需查询的数据映射到表中一个位置来访问记录,这加快了查找速度。这个映射函数称做散列函数,存放记录的数组称做散列表。
- 若关键字为{\displaystyle k}
,则其值存放在{\displaystyle f(k)}
的存储位置上。由此,不需比较便可直接取得所查记录。称这个对应关系{\displaystyle f}
为散列函数,按这个思想建立的表为散列表。
- 对不同的关键字可能得到同一散列地址,即{\displaystyle k_{1}\neq k_{2}}
,而{\displaystyle f(k_{1})=f(k_{2})}
,这种现象称为冲突(英语:Collision)。具有相同函数值的关键字对该散列函数来说称做同义词。综上所述,根据散列函数{\displaystyle f(k)}
和处理冲突的方法将一组关键字映射到一个有限的连续的地址集(区间)上,并以关键字在地址集中的“像”作为记录在表中的存储位置,这种表便称为散列表,这一映射过程称为散列造表或散列,所得的存储位置称散列地址。
- 若对于关键字集合中的任一个关键字,经散列函数映象到地址集合中任何一个地址的概率是相等的,则称此类散列函数为均匀散列函数(Uniform Hash function),这就是使关键字经过散列函数得到一个“随机的地址”,从而减少冲突。
散列函数能使对一个数据序列的访问过程更加迅速有效,通过散列函数,数据元素将被更快定位。
直接定址法,数字分析法,平方取中法,折叠法,随机数法,除留取余法
如何处理冲突
为了知道冲突产生的相同散列函数地址所对应的关键字,必须选用另外的散列函数,或者对冲突结果进行处理。而不发生冲突的可能性是非常之小的,所以通常对冲突进行处理。常用方法有以下几种:
- 开放定址法(open addressing):{\displaystyle hash_{i}=(hash(key)+d_{i})\,{\bmod {\,}}m}
, {\displaystyle i=1,2...k\,(k\leq m-1)}
,其中{\displaystyle hash(key)}
为散列函数,{\displaystyle m}
为散列表长,{\displaystyle d_{i}}
为增量序列,{\displaystyle i}
为已发生冲突的次数。增量序列可有下列取法:
-
{\displaystyle d_{i}=1,2,3...(m-1)}
称为 线性探测(Linear Probing);即 {\displaystyle d_{i}=i}
,或者为其他线性函数。相当于逐个探测存放地址的表,直到查找到一个空单元,把散列地址存放在该空单元。
-
{\displaystyle d_{i}=\pm 1^{2},\pm 2^{2},\pm 3^{2}...\pm k^{2}}
{\displaystyle (k\leq m/2)}
称为 平方探测(Quadratic Probing)。相对线性探测,相当于发生冲突时探测间隔 {\displaystyle d_{i}=i^{2}}
个单元的位置是否为空,如果为空,将地址存放进去。
-
{\displaystyle d_{i}=}
伪随机数序列,称为 伪随机探测。
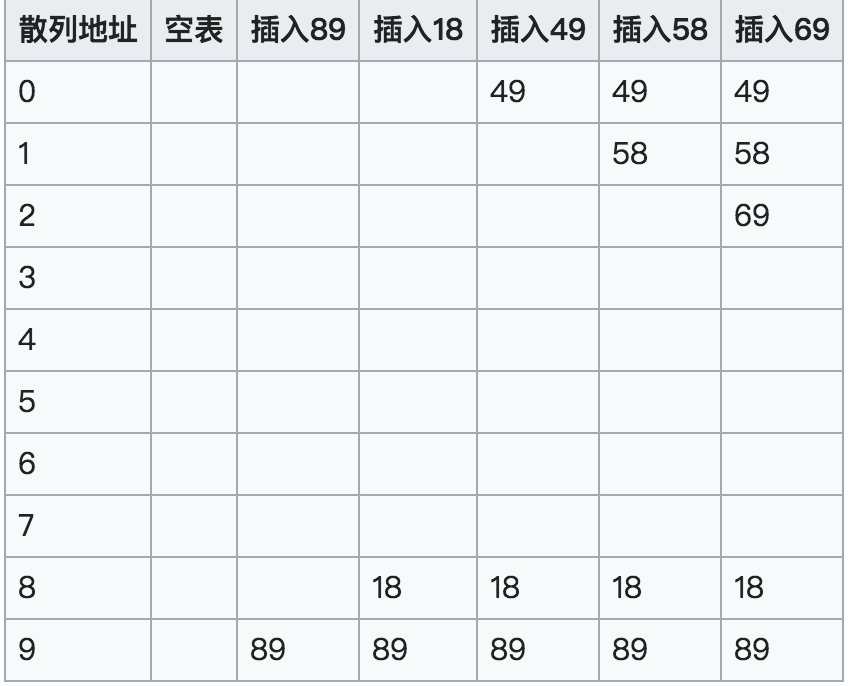
显示线性探测填装一个散列表的过程:
关键字为{89,18,49,58,69}插入到一个散列表中的情况。此时线性探测的方法是取{\displaystyle d_{i}=i}
-
第一次冲突发生在填装49的时候。地址为9的单元已经填装了89这个关键字,所以取
{\displaystyle i=1}
,往下查找一个单位,发现为空,所以将49填装在地址为0的空单元。第二次冲突则发生在58上,取 {\displaystyle i=2}
,往下查找两个单位,将58填装在地址为1的空单元。69同理。
- 表的大小选取至关重要,此处选取10作为大小,发生冲突的几率就比选择质数11作为大小的可能性大。越是质数,mod取余就越可能均匀分布在表的各处。
聚集(Cluster,也翻译做“堆积”)的意思是,在函数地址的表中,散列函数的结果不均匀地占据表的单元,形成区块,造成线性探测产生一次聚集(primary clustering)和平方探测的二次聚集(secondary clustering),散列到区块中的任何关键字需要查找多次试选单元才能插入表中,解决冲突,造成时间浪费。对于开放定址法,聚集会造成性能的灾难性损失,是必须避免的。
- 双散列。
- 再散列:{\displaystyle hash_{i}=hash_{i}(key)}
, {\displaystyle i=1,2...k}
。{\displaystyle hash_{i}}
是一些散列函数。即在上次散列计算发生冲突时,利用该次冲突的散列函数地址产生新的散列函数地址,直到冲突不再发生。这种方法不易产生“聚集”(Cluster),但增加了计算时间。
- 建立一个公共溢出区
影响产生冲突多少有以下三个因素:
- 散列函数是否均匀;
- 处理冲突的方法;
- 散列表的载荷因子(英语:load factor)。
载荷因子
散列表的载荷因子定义为:{\displaystyle \alpha }
{\displaystyle \alpha }




对于开放定址法,荷载因子是特别重要因素,应严格限制在0.7-0.8以下。超过0.8,查表时的CPU缓存不命中(cache missing)按照指数曲线上升。因此,一些采用开放定址法的hash库,如Java的系统库限制了荷载因子为0.75,超过此值将resize散列表。
什么是哈希表?
哈希表(Hash table,也叫散列表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
哈希表hashtable(key,value) 的做法其实很简单,就是把Key通过一个固定的算法函数既所谓的哈希函数转换成一个整型数字,然后就将该数字对数组长度进行取余,取余结果就当作数组的下标,将value存储在以该数字为下标的数组空间里。
而当使用哈希表进行查询的时候,就是再次使用哈希函数将key转换为对应的数组下标,并定位到该空间获取value,如此一来,就可以充分利用到数组的定位性能进行数据定位
博客例子
第一部分:百度算法题目
问题描述
百度面试题:
搜索引擎会通过日志文件把用户每次检索使用的所有检索串都记录下来,每个查询串的长度为1-255字节。
假设目前有一千万个记录(这些查询串的重复度比较高,虽然总数是1千万,但如果除去重复后,不超过3百万个。一个查询串的重复度越高,说明查询它的用户越多,也就是越热门。),请你统计最热门的10个查询串,要求使用的内存不能超过1G。
问题解析:
要统计最热门查询,首先就是要统计每个Query出现的次数,然后根据统计结果,找出Top 10。所以我们可以基于这个思路分两步来设计该算法。
即,此问题的解决分为以下俩个步骤:
第一步:Query统计
Query统计有以下俩个方法,可供选择:
1、直接排序法
首先我们最先想到的的算法就是排序了,首先对这个日志里面的所有Query都进行排序,然后再遍历排好序的Query,统计每个Query出现的次数了。
但是题目中有明确要求,那就是内存不能超过1G,一千万条记录,每条记录是255Byte,很显然要占据2.375G内存,这个条件就不满足要求了。
让我们回忆一下数据结构课程上的内容,当数据量比较大而且内存无法装下的时候,我们可以采用外排序的方法来进行排序,这里我们可以采用归并排序,因为归并排序有一个比较好的时间复杂度O(NlgN)。
排完序之后我们再对已经有序的Query文件进行遍历,统计每个Query出现的次数,再次写入文件中。
综合分析一下,排序的时间复杂度是O(NlgN),而遍历的时间复杂度是O(N),因此该算法的总体时间复杂度就是O(N+NlgN)=O(NlgN)。
2、Hash Table法
在第1个方法中,我们采用了排序的办法来统计每个Query出现的次数,时间复杂度是NlgN,那么能不能有更好的方法来存储,而时间复杂度更低呢?
题目中说明了,虽然有一千万个Query,但是由于重复度比较高,因此事实上只有300万的Query,每个Query255Byte,因此我们可以考虑把他们都放进内存中去,而现在只是需要一个合适的数据结构,在这里,Hash Table绝对是我们优先的选择,因为Hash Table的查询速度非常的快,几乎是O(1)的时间复杂度。
那么,我们的算法就有了:维护一个Key为Query字串,Value为该Query出现次数的HashTable,每次读取一个Query,如果该字串不在Table中,那么加入该字串,并且将Value值设为1;如果该字串在Table中,那么将该字串的计数加一即可。最终我们在O(N)的时间复杂度内完成了对该海量数据的处理。
本方法相比算法1:在时间复杂度上提高了一个数量级,为O(N),但不仅仅是时间复杂度上的优化,该方法只需要IO数据文件一次,而算法1的IO次数较多的,因此该算法2比算法1在工程上有更好的可操作性。
第二步:找出Top 10
算法一:普通排序
我想对于排序算法大家都已经不陌生了,这里不在赘述,我们要注意的是排序算法的时间复杂度是NlgN,在本题目中,三百万条记录,用1G内存是可以存下的。
算法二:部分排序(10容器大小的数组遍历 N*K)
题目要求是求出Top 10,因此我们没有必要对所有的Query都进行排序,我们只需要维护一个10个大小的数组,初始化放入10个Query,按照每个Query的统计次数由大到小排序,然后遍历这300万条记录,每读一条记录就和数组最后一个Query对比,如果小于这个Query,那么继续遍历,否则,将数组中最后一条数据淘汰,加入当前的Query。最后当所有的数据都遍历完毕之后,那么这个数组中的10个Query便是我们要找的Top10了。
不难分析出,这样,算法的最坏时间复杂度是N*K, 其中K是指top多少。
算法三:堆(二叉树遍历N*Log(K))
在算法二中,我们已经将时间复杂度由NlogN优化到NK,不得不说这是一个比较大的改进了,可是有没有更好的办法呢?
分析一下,在算法二中,每次比较完成之后,需要的操作复杂度都是K,因为要把元素插入到一个线性表之中,而且采用的是顺序比较。这里我们注意一下,该数组是有序的,一次我们每次查找的时候可以采用二分的方法查找,这样操作的复杂度就降到了logK,可是,随之而来的问题就是数据移动,因为移动数据次数增多了。不过,这个算法还是比算法二有了改进。
基于以上的分析,我们想想,有没有一种既能快速查找,又能快速移动元素的数据结构呢?回答是肯定的,那就是堆。
借助堆结构,我们可以在log量级的时间内查找和调整/移动。因此到这里,我们的算法可以改进为这样,维护一个K(该题目中是10)大小的小根堆,然后遍历300万的Query,分别和根元素进行对比。
具体过程是,堆顶存放的是整个堆中最小的数,现在遍历N个数,把最先遍历到的k个数存放到最小堆中,并假设它们就是我们要找的最大的k个数,X1>X2...Xmin(堆顶),而后遍历后续的N-K个数,一一与堆顶元素进行比较,如果遍历到的Xi大于堆顶元素Xmin,则把Xi放入堆中,而后更新整个堆,更新的时间复杂度为logK,如果Xi<Xmin,则不更新堆,整个过程的复杂度为O(K)+O((N-K)*logK)=O(N*logK)。
(堆排序的3D动画演示可以参看此链接:点击打开链接)
思想与上述算法二一致,只是算法在算法三,我们采用了最小堆这种数据结构代替数组,把查找目标元素的时间复杂度有O(K)降到了O(logK)。
那么这样,采用堆数据结构,算法三,最终的时间复杂度就降到了N‘logK,和算法二相比,又有了比较大的改进。
最小堆其实就是完全二叉树,顶部数据是最小的,每次比较堆顶的数据,然后继续调整结构为最小堆,继续比较
总结:
至此,算法就完全结束了,经过上述第一步、先用Hash表统计每个Query出现的次数,O(N);然后第二步、采用堆数据结构找出Top 10,N*O(logK)。所以,我们最终的时间复杂度是:O(N) + N'*O(logK)。(N为1000万,N’为300万)。如果各位有什么更好的算法,欢迎留言评论。
此外,还可以看下此文第二部分的第二题:点击打开链接。
补充:这种Top k问题更清晰的解释
先理解下什么是最小堆(点击打开链接)
先拿10000个数建堆,然后一次添加剩余元素,如果大于堆顶的数(10000中最小的),将这个数替换堆顶,并调整结构使之仍然是一个最小堆,这样,遍历完后,堆中的10000个数就是所需的最大的10000个。建堆时间复杂度是O(mlogm),算法的时间复杂度为O(nmlogm)(n为10亿,m为10000)。
优化的方法:可以把所有10亿个数据分组存放,比如分别放在1000个文件中。这样处理就可以分别在每个文件的10^6个数据中找出最大的10000个数,合并到一起在再找出最终的结果。
针对top K类问题,通常比较好的方案是分治+Trie树/hash+小顶堆(就是上面提到的最小堆),即先将数据集按照Hash方法分解成多个小数据集,然后使用Trie树活着Hash统计每个小数据集中的query词频,之后用小顶堆求出每个数据集中出现频率最高的前K个数,最后在所有top K中求出最终的top K。
以下是一些经常被提及的该类问题。
点击打开链接(1)有10000000个记录,这些查询串的重复度比较高,如果除去重复后,不超过3000000个。一个查询串的重复度越高,说明查询它的用户越多,也就是越热门。请统计最热门的10个查询串,要求使用的内存不能超过1GB。
(2)有10个文件,每个文件1GB,每个文件的每一行存放的都是用户的query,每个文件的query都可能重复。按照query的频度排序。
(3)有一个1GB大小的文件,里面的每一行是一个词,词的大小不超过16个字节,内存限制大小是1MB。返回频数最高的100个词。
(4)提取某日访问网站次数最多的那个IP。
(5)10亿个整数找出重复次数最多的100个整数。
(6)搜索的输入信息是一个字符串,统计300万条输入信息中最热门的前10条,每次输入的一个字符串为不超过255B,内存使用只有1GB。
(7)有1000万个身份证号以及他们对应的数据,身份证号可能重复,找出出现次数最多的身份证号。
总结:
一种问题是已经有数据集,直接查找出对应的top k,用k来做最小堆,进行遍历;
还有一种是未去重的,需要自己用常规快排+统计,或者用Hash Table进行数据处理,然后再根据最小堆的操作进行遍历。具体操作上面有介绍
第二部分:哈希表详解
Hash,一般翻译做“散列”,也有直接音译为“哈希”的,就是把任意长度的输入(又叫做预映射, pre-image),通过散列算法,变换成固定长度的输出,该输出就是散列值。这种转换是一种压缩映射,也就是,散列值的空间通常远小于输入的空间,不同的输入可能会散列成相同的输出,而不可能从散列值来唯一的确定输入值。简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。
HASH主要用于信息安全领域中加密算法,它把一些不同长度的信息转化成杂乱的128位的编码,这些编码值叫做HASH值. 也可以说,hash就是找到一种数据内容和数据存放地址之间的映射关系。
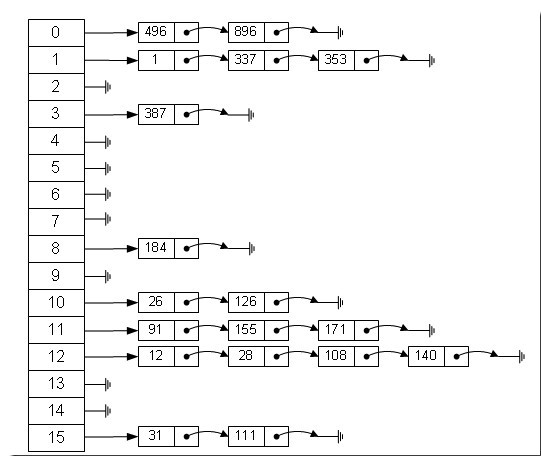
数组的特点是:寻址容易,插入和删除困难;而链表的特点是:寻址困难,插入和删除容易。那么我们能不能综合两者的特性,做出一种寻址容易,插入删除也容易的数据结构?答案是肯定的,这就是我们要提起的哈希表,哈希表有多种不同的实现方法,我接下来解释的是最常用的一种方法——拉链法,我们可以理解为“链表的数组”,如图:
链表法
左边很明显是个数组,数组的每个成员包括一个指针,指向一个链表的头,当然这个链表可能为空,也可能元素很多。我们根据元素的一些特征把元素分配到不同的链表中去,也是根据这些特征,找到正确的链表,再从链表中找出这个元素。
元素特征转变为数组下标的方法就是散列法。散列法当然不止一种,下面列出三种比较常用的:
直接定址法,数字分析法,平方取中法,折叠法,随机数法,除留取余法 这些方法可以在维基百科上找到
适用范围
快速查找,删除的基本数据结构,通常需要总数据量可以放入内存。
基本原理及要点
hash函数选择,针对字符串,整数,排列,具体相应的hash方法。
碰撞处理,一种是open hashing,也称为拉链法(链表法);另一种就是closed hashing,也称开地址法,opened addressing。
开放定址法(线性探测)
下面简单看下开地址法:点击打开链接
将关键字序列{7, 8, 30, 11, 18, 9, 14}散列存储到散列表中。散列表的存储空间是一个下标从0开始的一维数组,长度为10,即{0, 1,2, 3, 4, 5, 6, 7, 8, 9}。散列函数为: H(key) = (key * 3) % 7,处理冲突采用线性探测再散列法。
求等概率情况下查找成功和查找不成功的平均查找长度
解:
1 求散列表
H(7) = (7 * 3) % 7 = 0
H(8) = (8 * 3) % 7 = 3
H(30) = 6
H(11) = 5
H(18) = 5
H(9) = 6
H(14) = 0
按关键字序列顺序依次向哈希表中填入,发生冲突后按照“线性探测”探测到第一个空位置填入。
| address | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| key | 7 | 14 | 8 | 11 | 30 | 18 | 9 |
插入key = 18时,根据H(18) = 5应插在addresss=5的位置,但是address=5已经被key=11占据了,所以往后挪一位到address=6的位置,但是address=6被key=30占据了,再往后挪一位到address=7的位置,这个位置是空的,所以key=18就插到这个位置。
插入key = 9时,根据H(9) = 6应插在address=6的位置,但address = 6已经被key = 30占据,所以需要往后挪一位到address = 7的位置,但是address = 7已经被key = 18占据,所以再往后挪移到address = 8的位置,这个位置是空的,所以key = 9就插到这个位置。
插入key=14时,根据H(14) = 0应插在address=0的位置,但address=0被key=7占据,所以往后挪移一位到address=1的位置,这个位置是空的,所以key=14就插到这个位置。
2 求查找成功的平均查找长度
查找7,H(7) = 0,在0的位置,一下子就找到了7,查找长度为1。
查找8,H(8) = 3,在3的位置,一下子就找到了8,查找长度为1。
查找30,H(30) = 6,在6的位置,一下子就找到了30,查找长度为1。
查找11,H(11) = 5,在5的位置,一下子就找到了11,查找长度为1。
查找18,H(18) = 5,第一次在5的位置没有找到18,第二次往后挪移一位到6的位置,仍没有找到,第三次再往后挪移一位到7的位置,找到了,查找长度为3。
查找9,H(9) = 6,第一次在6的位置没找到9,第二次往后挪移一位到7的位置,仍没有找到,第三次再往后挪移一位到8的位置,找到了,查找长度为3.
查找14,H(14) = 0,第一次在0的位置没找到14,第二次往后挪移一位到1的位置,找到了,查找长度为2。
| address | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| key | 7 | 14 | 8 | 11 | 30 | 18 | 9 | |||
| length | 1 | 2 | 1 | 1 | 1 | 3 | 3 |
所以,查找成功的平均查找长度为(1 + 1 + 1 + 1 + 3 + 3 + 2) / 7 = 12 / 7。
3 求查找不成功的平均查找长度
| address | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| key | 7 | 14 | 8 | 11 | 30 | 18 | 9 |
查找不成功,说明要查找的数字肯定不在上述的散列表中。
因为这里哈希函数的模为7,所以要查找的数只可能位于0~6的位置上。
(1)若要查找的数key对应的地址为0,有(key * 3) % 7 = 0。
因为key不属于{7, 8, 30, 11, 18, 9, 14},可设key = 28。
第一次查找,address = 0时key = 7,不是要找的28,
第二次查找,往后挪移一位,address = 1时key = 14,不是要找的28;
第三次查找,往后再挪移一位,address = 2时key为空。可知查找不成功,否则28应该放在adress = 2的位置上。
结论:查找3次可知查找不成功。
(2)若要查找的数key 对应的地址为1,有(key * 3) % 7 = 1。
因为key不属于{7, 8, 30, 11, 18, 9, 14},可设key = 5。
第一次address = 1时key = 14,不是要找的5
第二次adress = 2时key为空。可知查找不成功,否则key = 5应该放在adress=1的位置上。
结论:查找2次可知查找不成功。
(3)若要查找的数key对应的地址为2,有(key * 3) % 7 = 2。
因为key不属于{7, 8, 30, 11, 18, 9, 14},可设key = 3。
第一次查找,address = 2时key为空。可知查找不成功,否则key = 3应该放在address = 2的位置。
结论:查找1次可知查找不成功。
(4)若要查找的数key对应的地址为3,有(key * 3) % 7 = 3。
因为key不属于{7, 8, 30, 11, 18, 9, 14},可设key = 15。
第一次查找,address = 3时key = 8,不是要找的15.
第二次查找,往后挪移一位,address = 4时key为空。可知查找不成功,否则key = 15会放在address = 4的位置上。
结论:查找2次可知查找不成功。
(5)若要查找的数key对应的地址为4,有(key * 3) % 7 = 4。
因为key不属于{7, 8, 30, 11, 18, 9, 14},可设key = 6。
第一次查找,address = 4时key为空。可知查找不成功,否则key = 6会放在address = 4的位置上。
结论:查找1次可知查找不成功。
(6)若要查找的数key对应的地址为5,有(key * 3) % 7 = 5。
因为key不属于{7, 8, 30, 11, 18, 9, 14},可设key = 4。
第一次查找,address = 5时key = 11,不是要找的4.
第二次查找,往后挪移一位,address = 6时key=30,不是要找的4。
第三次查找,往后再挪移一位,注意此时address = 0而非address = 7,因为模为7,决定了要查找的数只可能位于0~6的位置上。address = 0时key = 7,不是要找的4。
第四次查找,往后再挪移一位,address = 1时key = 14,不是要找的4。
第五次查找,往后再挪移一位,address = 2时key为空。可知查找不成功,否则key = 4会放在address = 2的位置上。
结论:查找5次可知查找不成功。
(7)若要查找的数key对应的地址为5,同理可得出结论:查找4次可知查找不成功。
综上,查找不成功的次数表如下所示
所以,查找不成功的平均查找长度为(3 + 2 + 1 + 2 + 1 + 5 + 4)/ 7 = 18 / 7
优点:
不论哈希表中有多少数据,查找、插入、删除(有时包括删除)只需要接近常量的时间即0(1)的时间级。实际上,这只需要几条机器指令。
哈希表运算得非常快,在计算机程序中,如果需要在一秒种内查找上千条记录通常使用哈希表(例如拼写检查器)哈希表的速度明显比树快,树的操作通常需要O(N)的时间级。哈希表不仅速度快,编程实现也相对容易。
如果不需要有序遍历数据,并且可以提前预测数据量的大小。那么哈希表在速度和易用性方面是无与伦比的。
缺点:
它是基于数组的,数组创建后难于扩展,某些哈希表被基本填满时,性能下降得非常严重,所以程序员必须要清楚表中将要存储多少数据,或者准备好定期地把数据转移到更大的哈希表中,这是个费时的过程。
哈希表如何处理冲突?
首先在元素的关键字key和元素的存储位置p之间建立一个对应的关系f;让p=f(key),f为哈希函数,创建哈希表时,就是把Key通过一个固定的算法函数f既所谓的哈希函数转换成一个整型数字,然后就将该数字对数组长度进行取余,取余结果就当作数组的下标,将value存储在以该数字为下标的数组空间里。以后查找时,直接利用哈希函数计算出数组下标,直接取出对应的value
1.如何构造哈希函数?
原则:本身便于计算,计算出来的地址分布均匀,对于任意关键字key,计算出来的f(key)不同地址的概率相同,目的是尽量减少冲突的可能。
直接定址法,数字分析法,平方取中法,折叠法,随机数法,除留取余法
2.遇到冲突了如何解决?由于不可能完全避免冲突,也可以说如何设计合理的哈希表?
- 开放定址法 如果遇到相同的key对应同一个value,可以线性探测,具体操作参考上面图
- 再哈希法,定义多个哈希函数,冲突时,再进行哈希运算,直到,计算耗时
- 拉链法(链地址法)具体操作如上图
- 建立公共溢出区 凡是遇到冲突,用另一个哈希表来处理,隔离开来
第三部分:最快哈希算法Demo
有一个庞大的字符串数组,然后给你一个单独的字符串,让你从这个数组中查找是否有这个字符串并找到它,你会怎么做?
unsigned long HashString( char *lpszFileName, unsigned long dwHashType )
{
unsigned char *key = (unsigned char *)lpszFileName;
unsigned long seed1 = 0x7FED7FED;
unsigned long seed2 = 0xEEEEEEEE;
int ch;
while( *key != 0 )
{
ch = toupper(*key++);
seed1 = cryptTable[(dwHashType << 8) + ch] ^ (seed1 + seed2);
seed2 = ch + seed1 + seed2 + (seed2 << 5) + 3;
}
return seed1;
}void prepareCryptTable()
{
unsigned long seed = 0x00100001, index1 = 0, index2 = 0, i;
for( index1 = 0; index1 < 0x100; index1++ )
{
for( index2 = index1, i = 0; i < 5; i++, index2 += 0x100 )
{
unsigned long temp1, temp2;
seed = (seed * 125 + 3) % 0x2AAAAB;
temp1 = (seed & 0xFFFF) << 0x10;
seed = (seed * 125 + 3) % 0x2AAAAB;
temp2 = (seed & 0xFFFF);
cryptTable[index2] = ( temp1 | temp2 );
}
}
} int GetHashTablePos( har *lpszString, SOMESTRUCTURE *lpTable )
//lpszString要在Hash表中查找的字符串,lpTable为存储字符串Hash值的Hash表。
{
int nHash = HashString(lpszString); //调用上述函数二,返回要查找字符串lpszString的Hash值。
int nHashPos = nHash % nTableSize;
if ( lpTable[nHashPos].bExists && !strcmp( lpTable[nHashPos].pString, lpszString ) )
{ //如果找到的Hash值在表中存在,且要查找的字符串与表中对应位置的字符串相同,
return nHashPos; //则返回上述调用函数二后,找到的Hash值
}
else
{
return -1;
}
}看到此,我想大家都在想一个很严重的问题:“如果两个字符串在哈希表中对应的位置相同怎么办?”,毕竟一个数组容量是有限的,这种可能性很大。解决该问题的方法很多,我首先想到的就是用“链表”,感谢大学里学的数据结构教会了这个百试百灵的法宝,我遇到的很多算法都可以转化成链表来解决,只要在哈希表的每个入口挂一个链表,保存所有对应的字符串就OK了。
然而Blizzard的程序员使用的方法则是更精妙的方法。基本原理就是:他们在哈希表中不是用一个哈希值而是用三个哈希值来校验字符串。
MPQ使用文件名哈希表来跟踪内部的所有文件。但是这个表的格式与正常的哈希表有一些不同。首先,它没有使用哈希作为下标,把实际的文件名存储在表中用于验证,实际上它根本就没有存储文件名。而是使用了3种不同的哈希:一个用于哈希表的下标,两个用于验证。这两个验证哈希替代了实际文件名。
当然了,这样仍然会出现2个不同的文件名哈希到3个同样的哈希。但是这种情况发生的概率平均是:1:18889465931478580854784,这个概率对于任何人来说应该都是足够小的。现在再回到数据结构上,Blizzard使用的哈希表没有使用链表,而采用"顺延"的方式来解决问题,看看这个算法:
函数四、lpszString 为要在hash表中查找的字符串;lpTable 为存储字符串hash值的hash表;nTableSize 为hash表的长度:
typedef struct
{
int nHashA;
int nHashB;
char bExists;
......
} SOMESTRUCTRUE; key对应到哈希数组里面的单个结构体
int GetHashTablePos( char *lpszString, MPQHASHTABLE *lpTable, int nTableSize )
{
const int HASH_OFFSET = 0, HASH_A = 1, HASH_B = 2;
int nHash = HashString( lpszString, HASH_OFFSET );
int nHashA = HashString( lpszString, HASH_A );
int nHashB = HashString( lpszString, HASH_B );
int nHashStart = nHash % nTableSize;
int nHashPos = nHashStart;
while ( lpTable[nHashPos].bExists )
{
/*如果仅仅是判断在该表中时候存在这个字符串,就比较这两个hash值就可以了,不用对
*结构体中的字符串进行比较。这样会加快运行的速度?减少hash表占用的空间?这种
*方法一般应用在什么场合?*/
if ( lpTable[nHashPos].nHashA == nHashA
&& lpTable[nHashPos].nHashB == nHashB )
{
return nHashPos;
}
else
{
nHashPos = (nHashPos + 1) % nTableSize;
}
if (nHashPos == nHashStart)
break;
}
return -1;
}上述程序解释:
1.计算出字符串的三个哈希值(一个用来确定位置,另外两个用来校验)
2. 察看哈希表中的这个位置
3. 哈希表中这个位置为空吗?如果为空,则肯定该字符串不存在,返回-1。
4. 如果存在,则检查其他两个哈希值是否也匹配,如果匹配,则表示找到了该字符串,返回其Hash值。
5. 移到下一个位置,如果已经移到了表的末尾,则反绕到表的开始位置起继续查询 这里用的是开放定址法,线性探测法
6. 看看是不是又回到了原来的位置,如果是,则返回没找到
7. 回到3

























 2666
2666

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








