论文笔记五【复杂网络中的同步问题】

论文笔记_大作业PPT: 这是我自己做的配套PPT，仅供参考 (gitee.com)

一、什么因素影响复杂网络完全同步

当网络结构相同时，如果节点上的动力学系统不同，网络的同步稳定性是不同的。即：能使一种动力学系统同步的网络不一定能够使另外的动力学系统同步。

当节点上的动力学系统相同，但耦合方式、耦合强度不同，即：将该系统放在同样的网络结构上，动力学网络的同步稳定性仍有差异；

对于同一个动力学系统，相同的耦合方式和耦合强度，但网络结构不同，其对动力学网络的同步稳定性也有影响。

综上所述，动力学系统、耦合方式、耦合强度、网络结构等因素决定了动力学网络的同步稳定性，这一部分的讲解主要关注网络结构对网络同步能力的影响，尤其是小世界网络和无标度网络。

从前面的分析我们知道：最近邻耦合网络在N趋向于无穷时不可能达到同步，但是如果加入少量的长程边后，网络的平均路径明显缩短，它的同步化能力便会明显提高。通过这个现象，研究人员们产生了问题：是不是由于平均路径的缩短提高了复杂网络的同步化能力呢？复杂网络中其他结构特性对网络的同步起到了什么作用？究竟是哪些网络基本参数对于提高网络同步化能力起到了关键性作用？   

针对这些问题，研究人员们探究了特征根比率、度、平均路径、度分布和介数等网络的主要基本特性，对小世界网络和无标度网络的同步化能力的影响。

先从小世界网络开始。小世界网络中的任意两个节点之间的平均路径长度较短。这意味着在网络中的任意两个节点之间，平均而言，只需要经过少数几个节点就可以相互到达。这一特性使得信息在网络中的传播效率较高。也就是说，小世界网络中的节点倾向于与邻近的节点形成密集的连接，即具有较高的局部聚类性。

在小世界网络中，加边或重连概率p是一个关键参数，它描述了原始规则网络的边被重新连接为随机边的概率。具体就是随机选择网络中的一条边，将这条边的两个端点断开连接，以概率p，将其中一个端点连接到网络中的另一个随机选择的节点上，反之则恢复原样，将原来的两个端点重新连接起来。当概率p不断变化时，会对应产生多个具有不同网络基本特性的小世界网络模型。

不断加入新的长程边或不断重新连接边，网络的特征根比率会随着减小，也就是说，随着加边或重连概率p的增加，λn与λ2的比值会逐渐减小。这说明小世界网络的同步能力随着概率p增加而增强。λn比λ2是耦合矩阵的特征根比率，其中λn是最小特征根，λ2是第二大特征根。 

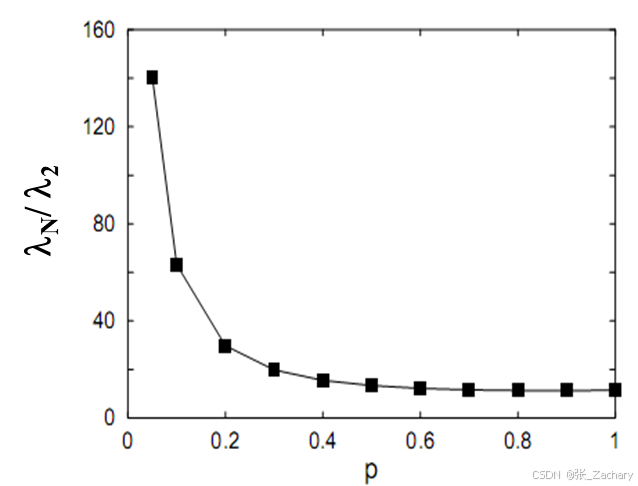
网络的平均度是指网络中所有节点的度的平均值。虽然小世界网络是均匀网络，但其网络中各个节点所连接的边数并不是完全相等的，因此用方差指标来表示节点度的分布。随着加边或重连概率p的增加，会使网络变得更不均匀，并且无论是加边还是重连边，网络中度的最大值都会增加，大图描述的是度分布的方差。方差越大说明网络中节点度的差距越大，也就是出现了度较大的节点。

网络平均路径长度是指网络中任意两个节点之间的距离的平均值，概率p的增加，也会使小世界网络的平均路径逐渐减小。0.5<p<1时，平均路径的变化不是很明显，如小图所示。

在最近邻耦合网络的基础上通过“小世界性”的操作，使得网络的平均路径长度减小，同时增加了网络节点度分布的非均匀性以及最大度，从而同步化能力有了显著的提高。总结来说，概率p的增加意味着节点的连接越来越紧密，更有利于网络同步。

接下来是无标度网络。无标度网络的特点是节点的度数分布呈现幂律分布，即少数节点具有极高的连接度（称为Hub节点），而大部分节点的连接度相对较低。这种网络模型反映了一些现实生活中的情况，即少数节点（也就是某个搜索引擎或某个明星）拥有大量的连接，而大多数节点则只有少量的连接。

幂律指数是描述幂律分布的一个关键参数，它决定了分布尾部的长度。幂律指数越小，表示网络中Hub节点的连接越强，即网络中真的存在极少数节点，拥有非常高的连接度。当幂律指数γ不断变化时，也会得到多个不同的无标度网络模型。

幂律指数值越大的网络，其特征根比率越小，说明幂律指数越大对应的无标度网络的同步化能力越强。幂律指数越大也意味着Hub节点的连接度并没有太高，网络中节点的度分布越均匀，这样的网络更容易实现同步，也符合我们的常识。

无标度网络可以通过少数度非常大的节点，将大量度很小的节点连接在一起，因此这些度大的节点使得网络的平均路径D很短。而随着幂律指数γ值的增大，网络度分布变得比较均匀，因此网络的平均路径D就会增加，同时平均度k变小。这样的操作使网络更容易同步。

如此看来，只有让网络分布得相对均匀一些，才更容易同步，而“相对均匀”又是一个比较抽象的概念。单纯使用度的大小、度分布或平均路径长度等指标都无法统一表征复杂网络的同步化能力。

所以我来介绍另外一个重要的因素，叫点介数。点介数是网络分析中用来衡量一个节点在网络中的中介作用的指标，它计算的是该节点在所有最短路径中出现的比例。具体来说，点介数高的节点在网络中扮演着重要的“桥梁”角色，它们在连接网络中的其他节点对方面起着关键作用。某个节点的介数越大说明在信息传播过程中通过该节点的信息量越多，于是也容易发生信息拥塞。

研究发现：无论是小世界网络还是无标度网络，节点的最大介数值都会随着概率p或参数γ的增大而减小。因此，要想提高网络同步化能力，就要减少最大介数，这张图是最大介数Bmax随连接概率p的变化图。

仿真实验表明：无论p为何值的小世界网络，当具有Bmax的节点去掉后，特征根比率均会下降，从而使网络的同步性能显著提高；相反，若随机去除一个节点，特征根比率前后没有很大变化，说明必须要对点介数大的节点进行操作，才会对整个网络同步性能产生影响。这是去除节点前后小世界网络特征根比率的变化图。结论就是，要想提高网络的同步能力，就应该减小节点的最大介数，不能让许多节点都经过同一个节点。    

此外，网络的社团结构和同型混合等特征都可能会影响网络的同步能力。因此，如何进一步从本质上刻画影响网络的同步因素仍是一个值得研究的课题。

二、改变耦合过程

刚刚提到某个节点的点介数过大的情况，实际上就是一种高耦合的情况，所以去耦合是可以增强网络的同步能力的。       

网络同步的过程同时也是耦合信息在网络中传输的过程，在信息传输过程中，如果信息量过大，网络中的中枢节点和重要的连边会出现拥塞现象，从而使信息传输的效率降低。如果能够使这些信息的传递路径重新导向，使得网络中的节点和连边的负荷达到比较平均的状态，无疑对网络中的信息传输是有益的。

改善方法其实就是结构扰动。1.  添加连边。2.  断开少量连边，达到信息负荷重新分配。我们使用BA网络，对每条边赋予一个量Gij＝Ki*Kj 度量该边的重要性， Ki和Kj是这条边两端顶点的度。例如，在每个时间步内，随机断开G值最大的某条边。BA网络是一种用于模拟和分析复杂网络结构的数学模型，主要描述无标度网络。在BA模型中，网络中的节点数目是不断增长的，逐步向网络中添加一个拥有m条边的新节点，模拟了网络的增长性，而新节点倾向于和链接数高的节点相连，即网络中节点的连接概率与其度成正比。

这张图展示了去耦合操作之后和之前的同步能力比值R’/R0与断开边的比例Ncut/N之间的关系，m指的是新加入节点时所带的边数，即新加入的节点将与网络中已有的m个节点建立连接。从斜率可以看出，断开的边越多，耦合性降低，网络的同步能力就会增强。       

我们希望去耦合的过程中，网络的统计特性基本不变，同时也考虑何种量和网络同步能力关联最大，因此我们讨论下述一些统计量的变化情况：1 ．度分布2． 平均距离3．簇系数4．最大介数。

第一，去耦合前后网络的度分布没有明显改变。在m等于5的情况下，去耦合前和去耦合后的度的分布情况基本一致，如散点所示。

第二，去耦合前后的网络平均距离也没有明显改变。在m取2、5、8的情况下，各自的斜率基本不变。

第三，去耦合后网络的簇系数显著降低。簇系数是衡量网络中节点的邻居之间相互连接程度的指标。它反映了网络中局部的紧密程度，即一个节点的邻居节点之间是否也相互连接。簇系数高表示网络中存在较多的三角形结构，即节点的邻居之间也相互连接，这通常意味着网络具有较强的局部连接性。

第四，是最大介数。从大图中可以看到，去耦合后最大介数显著降低，而小图又告诉我们，最大介数降低意味着网络的同步能力增强。       

总结一下，在第二部分的讲解中，我介绍了一种提高网络同步能力的方法，即去耦合，该方法可以通过对网络结构做很小的改变明显提高网络的同步能力，并且基本上完全保持了原有网络的无标度特性。同时考察了一些非常重要的网络结构统计特征量，包括平均距离、簇系数、度分布和节点最大介数，发现在所有我们考察的结构特征量中，节点最大介数看起来是最好的网络同步能力的表征参量。这也回答了我们在第一部分提出的问题。

三、网络模体的同步

同步现象除了整个网络的同步外，还需研究网络模体的同步。模体是各种网络中重复出现的相同的子图，一个子图便可以反映一个框架，这个框架可以有效地实现某个特定的功能。在实际网络中，模体刻画网络自身的一组特定的结构，辨别出这些模体有助于识别网络的典型的局部连接模式。模体不同于内部紧密连接的社团，模体描述的是因为网络生成过程中所涌现出的规律，而不是已完成的网络所呈现的局部密集的区域

模体具有直接的生物学意义。例如:酵母蛋白质交互作用网络中的模体组分高度进化保护，不同物种的转录水平调控网络中有朝着相同模体类型进化的趋势，在基因逻辑网络中，我们寻找出现频率较高的基因间作用方式，就是在发掘基因网络中模体。

这里有一张表格。当模体的规模固定时，不同的连接方式决定了不同模体结构的同步阈值。网络模体产生同步的概率为P，c是耦合强度。当同步概率P等于1/2时，我们用c*来表示当前的c值。显然，不同模体对应的c*各不相同。模体的c*越小，说明网络越容易达到同步。对于模体4，6，9，它们都是由四个节点构成，但连接节点的方式不同，结果是它们的c*差别很大，可以看到模体内部的连接越多，c*值就越小，比如模体9。

四、网络中的部分同步现象

网络中的部分同步现象是指在复杂网络中，并非所有节点都达到完全同步的状态，而是网络中的某些节点或子集合通过相互作用达到某种一致或协调的状态。这种现象在物理、生物和技术系统中都有重要的应用。

北京师范大学郑志刚小组研究了在规则网络上添加非局域连接所导致的部分同步现象，发现非局域连接能够使网络的动力学发生巨大的改变，使得规则网络的对称性遭到破坏，不同的连接方式会导致不同的部分同步时空斑图。

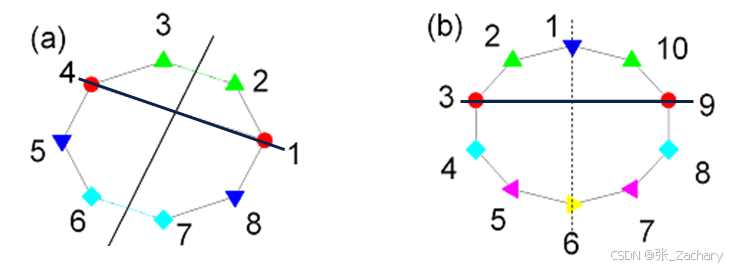
从图a中可以看到，一共有8个节点，连接节点1和节点4，可以使网络分成4个同步集团。节点1和4的连接是一条非局域连接。

从图b中可以看到，一共有10个节点，连接节点3和节点9，可以使网络分成6个同步集团，使用不同颜色标记出来了。

由此可见，部分同步总是伴随着网络的镜像对称轴而发生。

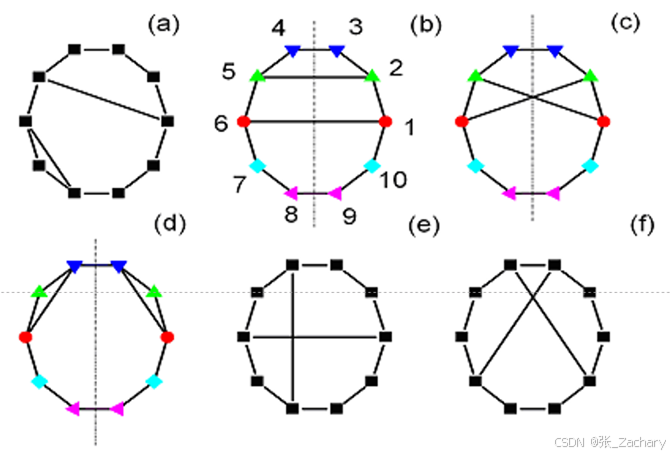
值得注意的是，不是说存在镜像对称轴就一定能够实现部分同步，也不是说部分同步就一定需要镜像对称轴。如图所示。（a）一种没有镜像对称性因而没有部分同步态的网络；（b）“平行”网络；（c）“交叉”网络；（d）“八字”网络；（e）和（f）：两种有镜像对称性却不能发生部分同步的网络。

上述结果体现了时空动力系统的网络拓扑结构对系统动力学的重大影响。一些特殊的网络结构，如非局域的连接，破坏了网络原有的对称性，使系统中没有了诸多对称性的竞争，而系统在剩下的对称性下出现了新的时空斑图。

五、总结

复杂网络作为一个实际复杂系统的模型，我们研究它的内在机理，即不同的动力学特性，例如：相继故障，同步现象，控制等，实际上就是在研究随着外界环境的变化，导致网络结构变化，复杂系统在不同动力学特性方面的自组织能力。若系统某一特性的自组织能力较弱，不能适应外界环境的变化，这就可能造成系统的这一特性减弱，甚至导致系统瘫痪。

关于复杂网络的同步问题，未来有一些研究工作可以关注。非线性网络中动力学复杂性、分岔、混沌、超混沌及时空混沌复杂性的分析、控制与同步，一直是一个重要课题。现在人们关心的问题是，具有小世界效应和无标度性质的复杂网络中分岔、混沌等动力学行为发生了什么变化？怎么实现这些复杂网络中所需动力学行为的控制与同步？在网络的不同区域能否实现网络中的平衡态和周期态的同步稳定控制？这是非线性系统中混沌控制与同步课题研究的延伸和深化发展。