广义随机森林算法（GRF）估计条件平均处理效果（CATE）

广义随机森林估计条件平均处理效果（CATE）

广义随机森林（generalized random forests)在R语言中的软件包叫做grf，其为异质治疗效果估计提供了非参数方法（可选使用右删失结果、多个治疗组或结果或工具变量），以及最小二乘回归、分位数回归和生存回归，所有这些都支持缺失的协变量。

此外，GRF 还支持“诚实”（honest）估计（其中数据的一个子集用于选择分割，另一个用于填充树的叶子），以及用于最小二乘回归和处理效果估计的置信区间。

安装步骤

可以通过 CRAN 安装最新版本的软件包：

install.packages("grf")

conda 用户可以从 conda-forge 通道进行安装：

conda install -c conda-forge r-grf

可以使用 devtools 从源安装当前开发版本。

devtools::install_github("grf-labs/grf", subdir = "r-package/grf")

使用GRF估计条件平均处理效果（CATE）

library(grf)

接下来我们将对广义随机森林（GRF）算法进行了简要概述，并包含两个示例应用：1）金融教育计划的益处；2）衡量贫困对注意力的影响，该部分详细介绍了如何使用广义随机森林来估计条件平均处理效应（CATEs）：

• [best_linear_projection]作为简单的线性关联度量，可以为条件平均处理效应（CATEs）提供有用的低维摘要，具有理想的半参数推断特性。
• [rank_average_treatment_effect]（RATE）作为一种通用工具，用于评估异质性和“目标规则”的有效性，以及相关的TOC曲线如何帮助识别对处理有不同反应的人群分段。
• [policytree]用于找到基于树的策略。

广义随机森林概述

本节以因果森林（Causal Forest）的工作原理为例，快速介绍广义随机森林（GRF）背后的一些概念性思想。它首先描述了在估计平均处理效应时，如何利用现代机器学习工具箱的预测能力进行非参数化控制混杂因素，以及如何将布雷曼（2001）的随机森林重新用作自适应最近邻查找器来检测处理效应的异质性。

用于因果推断的机器学习

机器学习算法在预测方面表现出色。然而，在估计处理效应的背景下，重要的是估计和推断（关于预测和估计之间基本张力的精彩概述，请参阅 Efron（2020）的文章）。下一节概述了如果经过仔细调整并与半参数统计的最佳实践相结合，现代机器学习如何能够用更多与模型无关的工具来扩充因果推断工具箱。

想象一下，我们观察到结果$Y_i$以及二元处理指标 W = { 0 , 1 } W=\{0,1\} W={0,1}，并且对测量干预对结果的平均因果效应感兴趣。如果我们不在随机对照试验环境中，但收集了一组协变量$X_i$，我们认为这些协变量可以合理地解释混杂因素，那么我们可以运行以下类型的回归（Imbens & Rubin，2005）：
$$Y_i\sim \tau W_i+\beta X_i,$$
并将估计的$\hat{\tau }$解释为平均处理效应$\tau =E[Y_i(1)-Y_i(0)]$的估计值，其中$Y_i(1),Y_i(0)$是对应于两种处理状态的潜在结果。如果满足以下条件，这种方法是合理的：

1. 给定$X_i$，$W_i$是无混杂的（即，给定协变量，处理效果与随机效果一样好）。
2. 混杂因素$X_i$对$Y_i$有线性影响。

假设 1）是一个我们必须接受的“识别性”假设，然而假设 2）和 3）是我们可以质疑的建模假设。让我们从假设 2）开始：这是一个强参数化建模假设，要求混杂因素对结果有线性影响，并且我们应该能够通过依赖半参数统计来放宽这个假设。

放宽假设 2）。我们可以转而假定部分线性模型：

$$Y_i=\tau W_i+f(X_i)+{\epsilon }_i,E[{\epsilon }_i|X_i,W_i]=0,$$
在这里，我们假设一个单位的基线结果由某个未知（可能很复杂）的函数$f$给出，并且处理分配会使结果产生一个恒定的偏移量$\tau$。但是，当我们不知道$f(X_i)$时，我们如何绕过对$\tau$的估计呢？Robinson（1988）表明，如果我们定义以下两个中间对象：

$$e(x)=E[W_i|X_i=x],$$
倾向得分，以及

$$m(x)=E[Y_i|X_i=x]=f(x)+\tau e(x),$$

如果已知(Y)的条件均值，那么我们可以将上述方程重写为“中心化”形式。
$$Y_i-m(x)=\tau (W_i-e(x))+{\epsilon }_i.$$
这种公式具有很大的实际吸引力，因为这意味着$\tau$可以通过残差对残差回归来估计：插入$m(x)$和$e(x)$的估计值，然后将中心化的结果对中心化的处理指标进行回归。Robinson（1988）表明，这种方法产生$\tau$的根-n 一致估计，即使$m(x)$和$e(x)$的估计以较慢的速度收敛（特别是“四次方根”）。这种性质通常被称为“正交性”，是一种理想的性质，它本质上告诉你，给定有噪声的“干扰”估计（$m(x)$和$e(x)$），你仍然可以恢复目标参数（$\tau$）的“良好”估计。

但是你应该如何估计$m(x)$和$e(x)$呢？你不是仍然需要假设一个参数模型（例如，用于倾向得分的逻辑回归）吗？这就是现代机器学习工具包派上用场的地方，因为认识到对于$m(x)$和$e(x)$，我们只是在寻求对给定$X_i$的结果以及给定$X_i$的处理分配的良好“预测”。这是现代机器学习方法（如提升、随机森林等）擅长的问题类型。直接将$m(x)$和$e(x)$的估计值插入到残差对残差回归中通常会导致偏差，因为现代机器学习方法会进行正则化以权衡偏差和方差，然而，Zheng & van der Laan（2011）和 Chernozhukov 等人（2018）表明，如果你以“交叉拟合”的方式形成这些估计值，即观测值$i$的结果和处理分配的预测是在不使用单位$i$进行估计的情况下获得的，那么（在一些正则性假设下）你仍然可以恢复$\tau$的根-n 一致估计。

所以，到目前为止回顾一下：我们有一种方法可以采用现代机器学习工具包，在估计平均处理效应时对混杂因素进行非参数控制，并且仍然保留理想的统计特性，如无偏性和一致性。

非恒定处理效应。如果我们希望放宽假设 3）会怎样呢？我们可以指定某些子组，对每个子组进行单独回归，并获得不同的$\tau$估计值。为了避免错误发现，这种方法要求我们在不查看数据的情况下指定潜在子组。我们如何使用数据来告知我们潜在的子组呢？我们可以继续使用上面的Robinson部分线性模型，而只需假设：

$$Y_i=\tau (X_i)W_i+f(X_i)+{\epsilon }_i,E[{\epsilon }_i|X_i,W_i]=0,$$

其中，$\tau (X_i)$是条件平均处理效应$E[Y(1)-Y(0)|X_i=x]$。我们如何估计这个呢？如果我们想象我们能够访问某个邻域$\mathcal{N}(x)$，其中$\tau$是恒定的，我们可以像以前一样进行操作，即对属于$\mathcal{N}(x)$的样本进行残差对残差回归，即：

τ ( x ) : = l m ( Y i − m ^ ( − i ) ( X i ) ∼ W i − e ^ ( − i ) ( X i ) , weights = 1 { X i ∈ N ( x ) } ) , \tau(x) := lm\Biggl( Y_i - \hat m^{(-i)}(X_i) \sim W_i - \hat e^{(-i)}(X_i), \text{weights} = 1\{X_i \in \mathcal{N}(x) \}\Biggr), τ(x):=lm(Yi​−m^(−i)(Xi​)∼Wi​−e^(−i)(Xi​),weights=1{Xi​∈N(x)}),
（上标${}^i$表示交叉拟合估计）。从概念上讲，这就是“因果森林”的作用，它通过对具有相似处理效应的样本进行加权残差对残差回归来估计目标样本$X_i=x$的处理效应$\tau (x)$。这些“权重”起着至关重要的作用，那么grf是如何找到它们的呢？下一节将快速回顾布雷曼的用于回归的随机森林，然后解释如何将其扩展为自适应邻域查找器。

随机森林作为一种自适应邻域查找器

布雷曼的随机森林用于预测条件均值$\mu (x)=E[Y_i|X_i=x]$可以简要概括为两个步骤：

• 1）构建阶段：构建$B$棵树，贪婪地放置协变量分割，以最大化子组均值的平方差$n_L{n}_R({\bar{y}}_L-{\bar{y}}_R{)}^2$。
• 2）预测阶段：聚合每棵树的预测，通过对与目标样本$x$落入相同终端叶节点$L_b(X_i)$的结果$Y_i$取平均值来形成最终的点估计。

μ ^ ( x ) = 1 B ∑ b = 1 B ∑ i = 1 n Y i 1 { X i ∈ L b ( x ) } ∣ L b ( x ) ∣ \hat \mu(x) = \frac{1}{B} \sum_{b=1}^{B} \sum_{i=1}^{n} \frac{Y_i 1\{Xi \in L_b(x)\}} {|L_b(x)|} μ^​(x)=B1​b=1∑B​i=1∑n​∣Lb​(x)∣Yi​1{Xi∈Lb​(x)}​

set.seed(2)
n = 20; p = 1
X = matrix(rnorm(n * p), n, p)
Y = X[, 1] + rnorm(n)
rf = regression_forest(X, Y, num.trees = 1, ci.group.size = 1, honesty = FALSE, sample.fraction = 1, num.threads = 1)
t = get_tree(rf, 1)
sval = t$nodes[[1]]$split_value

plot(c(X, 1.5), c(Y, 2),
     ylab = "Y",
     xlab = "X_j",
     col = c(as.integer(X[,1] <= sval) + 1, 4),
     pch = c(rep(1, n), 3))
abline(v = sval)

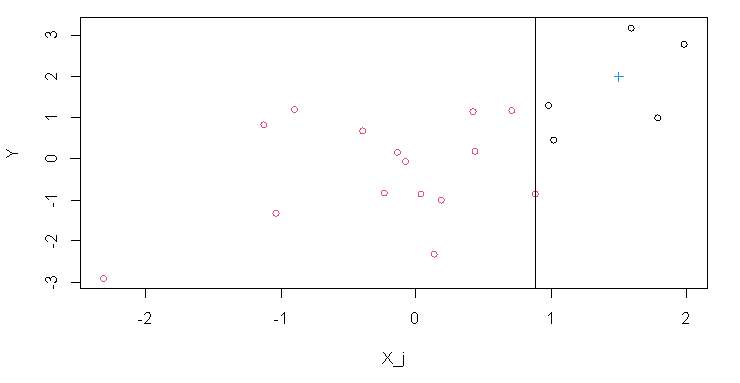
对于单个树和单个分割，图 1 展示了阶段 1 中的最佳分割点：它是使$Y_i$的左右均值尽可能相似的垂直线（或者等价地，使均值的平方差尽可能大）。

图 1 将我们希望进行预测的目标样本$x$表示为右侧叶中的十字。阶段 2 将对这一侧的$Y_i$取平均值，然后对其余的$B$棵树重复相同的操作，然后对这些结果取平均值以产生最终预测。这个过程是双重求和，首先对树求和，然后对训练样本求和。我们可以交换求和的顺序并得到：
μ ^ ( x ) = ∑ i = 1 n 1 B ∑ b = 1 B 1 { X i ∈ L b ( x ) } ∣ L b ( x ) ∣ Y i = ∑ i = 1 n Y i α i ( x ) \hat{\mu}(x) = \sum_{i = 1}^{n} \frac{1}{B} \sum_{b = 1}^{B} \frac{1_{\{X_i \in L_b(x)\}}}{\left|L_b(x)\right|} Y_i = \sum_{i = 1}^{n} Y_i\color{blue} \alpha_i(x) μ^​(x)=i=1∑n​B1​b=1∑B​∣Lb​(x)∣1{Xi​∈Lb​(x)}​​Yi​=i=1∑n​Yi​αi​(x)

我们将${\alpha }_i(x)$定义为第$i$个训练样本与$x$落入同一叶子节点的频率。也就是说，对随机森林预测阶段的等效描述是它预测结果的加权平均值。这些权重就是所谓的随机森林自适应邻域权重，它们捕捉到目标样本$x$与每个训练样本$X_i$（$i=1\dots n$）的“相似程度”（这种随机森林的加权观点在随机森林的统计应用中经常出现，例如参见 Zeileis、Hothorn 和 Hornik（2003））。

因果森林本质上结合了Breiman（2001）和Robinson（1988）的方法，通过将上述步骤修改为：

1. 构建阶段：贪婪地放置协变量分割，以最大化子组处理效应的平方差$n_L{n}_R({\hat{\tau }}_L-{\hat{\tau }}_R{)}^2$，其中$\hat{\tau }$是通过对每个可能的分割点运行罗宾逊的残差对残差回归得到的。
2. 使用得到的森林权重$\alpha (x)$来估计。

$$\tau (x):=lm(Y_i-{\hat{m}}^{(-i)}(X_i)\sim W_i-{\hat{e}}^{(-i)}(X_i),\text{weights}={\alpha }_i(x)).$$
也就是说，“因果森林”正在运行罗宾逊回归的“森林”局部版本。这种自适应加权（而非叶子平均）与其他一些被称为“诚实性”和“子采样”的森林构建细节相结合，可以为随机森林的估计和推断提供渐近保证（Wager & Athey，2018）。在函数“causal_forest”中，参数“Y.hat”和“W.hat”提供了$m(x)$和$e(x)$的估计值，默认情况下，这些值是通过单独的回归森林估计的。
我们上面概述的过程可以推广（因此得名“广义随机森林”），以估计除异质处理效应之外的其他量。关键要素是上述的阶段 1），通过认识到罗宾逊回归可以等效地以特定计分函数${\psi }_{\tau }(\cdot )$给出的“估计方程”形式表达。广义随机森林（Athey、Tibshirani 和 Wager，2019）将阶段 1）推广到以这个估计方程的解给出的某个任意参数中的异质性为目标。也就是说，广义随机森林本质上以如何在没有协变量的情况下估计某个参数$\theta$的公式（以计分函数$\psi$)的形式）作为输入，然后找到产生特定于协变量的估计$\alpha (x)$的森林权重 $\theta (x)$。

高效地估计处理效应(CATEs)

到目前为止，我们已经讨论了罗宾逊的残差在残差上如何满足正交性，即目标参数$\tau (x)$可以被合理地估计，尽管干扰成分（$m(x)$和$e(x)$）以较慢的速率被估计。这是估计方程$\psi$的一个理想特性，特别是如果我们希望使用机器学习方法来估计干扰成分，这些方法虽然比参数模型更灵活，但收敛速度较慢（斯通，1980）。那么，对于$\tau (x)$的摘要估计呢，就像平均处理效应（ATE）或最佳线性投影（BLP）这样的估计对象，它们保证了$n$的平方根收敛速度以及精确的置信区间？

结果表明，比起简单地对通过因果森林得到的$\hat{\tau }(x)$取平均值，存在更好的方法。Robins、Rotnitzky & Zhao（1994）表明，所谓的增强逆概率加权（AIPW）估计量对于$\tau$是渐近最优的（这意味着在所有非参数估计量中，它具有最低的方差）。它如下所示：

$${\hat{\tau }}_{AIPW}=\frac{1}{n}\sum _{i=1}^n\left(\mu (X_i,1)-\mu (X_i,0)+W_i\frac{Y_i-\mu (X_i,1)}{e(X_i)}-(1-W_i)\frac{Y_i-\mu (X_i,0)}{1-e(X_i)}\right),$$

其中，$\mu (X_i,1)$和$\mu (X_i,0)$是两个处理组中条件均值的估计值：
$\mu (X_i,W_i)=E[Y_i|X_i=x,W_i=w]$。这个表达式可以重新排列并表示为:

$$\begin{gathered} \frac{1}{n}\sum _{i=1}^n\left(\tau (X_i)+\frac{W_i-e(X_i)}{e(X_i)[1-e(X_i)]}\left(Y_i-\mu (X_i,W_i)\right)\right) \\ =\frac{1}{n}\sum _{i=1}^n{\Gamma }_i. \end{gathered}$$

我们可以将这三个术语确定为：1）初始处理效应估计值$\tau (X_i)$，2）去偏权重$\frac{W_i-e(X_i)}{e(X_i)[1-e(X_i)]}$，以及 3）残差$Y_i-\mu (X_i,W_i)$。如果我们代入使用因果森林获得的非参数干扰估计值（受一些正则条件的约束，如交叉拟合，Zheng & van der Laan（2011），Chernozhukov 等人（2018）），这种插件构造的渐近效率特性仍然成立。

一般来说，上述构造会产生所谓的“双重稳健”估计方程，这也是grf在计算诸如平均处理效应（ATE）、最佳线性投影（BLP）和“RATE”等汇总度量时所采用的方法。相关的双重稳健得分${\hat{\Gamma }}_i$可通过函数get_scores访问。举个具体的例子，平均处理效应是${\hat{\Gamma }}_i$的平均值，而最佳线性投影是${\hat{\Gamma }}_i$在一组协变量$X_i$上的回归。基于这些的汇总度量在解释非参数因果效应估计（CATE）中起着至关重要的作用，因为它们受到非参数估计（包括机器学习）的基本限制，是有噪声的点估计。接下来的两节将通过实证例子进行说明。

案例：学校项目评估

在本节中，我们将介绍广义随机森林（GRF）的一个示例应用。我们使用的数据来自布鲁恩等人（2016），他们在巴西进行了一项随机对照试验，在该试验中，高中被随机分配了一个金融教育项目（在这样的设置中，通常在学校层面进行随机化以避免学生层面的干扰）。这个项目平均提高了学生的金融素养。论文中考虑了其他结果，我们在这里将重点关注金融素养得分。这个数据的处理副本包含了大约 17000 名学生的学生层面数据，存储在github 存储库中，它提取了学生的基本特征，以及我们用作协变量的其他基线调查响应（其中两个由作者聚合为一个指数，以评估学生的储蓄能力和他们的财务自主性）。

“注意”：在整个过程中，我们使用变量名“Y”和“W”表示结果和二元处理分配，“Y.hat”表示对$E[Y_i|X_i=x]$的估计，“W.hat”表示对$E[W_i|X_i=x]$的估计，“tau.hat”表示对$\tau (X_i)=E[Y_i(1)-Y_i(0)|X_i=x]$的估计。

数据概述

data <- read.csv("data/bruhn2016.csv")
Y <- data$outcome
W <- data$treatment
school <- data$school
X <- data[-(1:3)]

# Around 30% have one or more missing covariates, the missingness pattern doesn't seem
# to vary systematically between the treated and controls, so we'll keep them in the analysis
# since GRF supports splitting on X's with missing values.
sum(!complete.cases(X)) / nrow(X)
#> [1] 0.29
t.test(W ~ !complete.cases(X))
#> 
#>  Welch Two Sample t-test
#> 
#> data:  W by !complete.cases(X)
#> t = -0.4, df = 9490, p-value = 0.7
#> alternative hypothesis: true difference in means between group FALSE and group TRUE is not equal to 0
#> 95 percent confidence interval:
#>  -0.020  0.013
#> sample estimates:
#> mean in group FALSE  mean in group TRUE 
#>                0.51                0.52

估计和总结条件平均处理效应（CATEs）

在整个过程中，我们将倾向得分固定为“W.hat = 0.5”，因为我们知道这是一项随机对照试验（否则我们将为“W.hat”拟合一个倾向模型，并检查估计概率的直方图以评估重叠假设的合理性）。

cf <- causal_forest(X, Y, W, W.hat = 0.5, clusters = school)

计算一个双重稳健的平均处理效应估计值。

ate <- average_treatment_effect(cf)
ate
#> estimate  std.err 
#>     4.35     0.52

与整体结果量表相比，益处似乎相当大。ate[1] / sd(Y)= r ate[1] / sd(Y), 并且与 Bruhn 等人（2016）的研究一致。

一种非常简单的方法来查看哪些变量似乎对处理效果有影响，就是检查“变量重要性”，它衡量变量$X_j$被分割的频率。

varimp <- variable_importance(cf)
ranked.vars <- order(varimp, decreasing = TRUE)

# Top 5 variables according to this measure
colnames(X)[ranked.vars[1:5]]
#> [1] "financial.autonomy.index"        "intention.to.save.index"        
#> [3] "family.receives.cash.transfer"   "father.attened.secondary.school"
#> [5] "is.female"

CATE 的一种易于解释的汇总度量是最佳线性投影，它为线性模型提供了双重稳健估计。

$\tau (X_i)={\beta }_0+A_i\beta$，其中$A_i$是协变量向量。如果我们将(A)设置为具有最高变量重要性的协变量，我们可以估计 CATEs 的简单线性关联度量：

best_linear_projection(cf, X[ranked.vars[1:5]])
#> 
#> Best linear projection of the conditional average treatment effect.
#> Confidence intervals are cluster- and heteroskedasticity-robust (HC3):
#> 
#>                                 Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)                      6.76430    1.04573    6.47    1e-10 ***
#> financial.autonomy.index        -0.02713    0.01414   -1.92    0.055 .  
#> intention.to.save.index         -0.00866    0.01585   -0.55    0.585    
#> family.receives.cash.transfer   -1.11185    0.65810   -1.69    0.091 .  
#> father.attened.secondary.school  0.60338    0.58694    1.03    0.304    
#> is.female                       -0.87818    0.53100   -1.65    0.098 .  
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

查看最佳线性投影（BLP），似乎具有高“财务自主指数”的学生从治疗中受益较少。随机对照试验的作者写道，这是一个“基于心理学的财务自主指数，它汇总了一系列问题，用于衡量学生是否感到有能力、有信心并能够做出独立的财务决策以及影响家庭的财务决策”。BLP 似乎表明，按照这个指数衡量已经在财务上舒适的学生，从培训课程中受益不多。

用RATE评估CATE估计值

因果推断从根本上比具有明确定义的评分指标（如预测误差）的机器学习算法的典型预测用途更具挑战性。处理效应从根本上是不可观测的，所以我们需要替代指标来评估性能。Nie 和 Wager（2021）中讨论的“R 损失”就是这样一种指标，例如，它可以用作交叉验证标准，然而，它并没有告诉我们是否存在异质处理效应。即使真实的处理效应是不可观测的，我们可以使用对保留数据的处理效应的合适“估计”来评估模型。“秩加权平均处理效应”（RATE）（Yadlowsky 等人，2022）是一种指标，用于评估CATE 估计器根据估计的处理效益对单位进行排序的效果。它可以被视为异质性的曲线下面积（AUC）度量，数值越大越好。

RATE 具有吸引人的视觉成分，因为它是曲线下的面积，在改变处理部分$q\in [0,1]$时，描绘出以下预期值的差异。

$$TOC(q)=E[Y_i(1)-Y_i(0)|\hat{\tau }(X_i)\ge F_{\hat{\tau }(X_i)}^{-1}(1-q)]-E[Y_i(1)-Y_i(0)],$$
（$F(\cdot )$是分布函数）。即当$q=0.2$时，TOC 量化了仅治疗具有最大估计 CATE 的 20%与总体 ATE 相比的增量效益。我们将 TOC 下的面积称为AUTOC，还有其他 RATE 指标，如Qini，它对 TOC 下的面积进行不同的加权。

使用 RATE 进行有效推断的一个方法是将数据分为训练集和评估集，一个用于评估 RATE，另一个用于训练 CATE 估计器。这种方法的一个缺点是，我们可能会根据用于定义评估集和训练集的随机样本检测到不同的结果。由于随机对照试验是在学校层面进行聚类的，所以我们将在学校层面抽取随机单位。

samples.by.school <- split(seq_along(school), school)
num.schools <- length(samples.by.school)
train <- unlist(samples.by.school[sample(1:num.schools, num.schools / 2)])

train.forest <- causal_forest(X[train, ], Y[train], W[train], W.hat = 0.5, clusters = school[train])
tau.hat.eval <- predict(train.forest, X[-train, ])$predictions

eval.forest <- causal_forest(X[-train, ], Y[-train], W[-train], W.hat = 0.5, clusters = school[-train])

rate.cate <- rank_average_treatment_effect(eval.forest, tau.hat.eval)
plot(rate.cate, main = "TOC: By decreasing estimated CATE")

rate.cate
#>  estimate std.err             target
#>      0.41    0.33 priorities | AUTOC

对于这个特定的数据集，RATE 是否显著取决于 CATE 估计器是否在具有足够信号的子样本上进行训练（使用不同方法（例如提升或惩罚线性模型）训练Y.hat的模型有时可能是有用的）。除了 CATE 排名之外，还有更多利用 RATE 指标的方法，例如，我们可以通过特定变量的排名来计算 TOC。上一节表明，具有高财务自主权的学生从该项目中受益较少。我们可以使用 RATE 来评估基于此指标对学生进行优先排序的效果。

# 由于我们是基于一个协变量来计算比率，所以我们在完整数据上使用经过训练的森林。
rate.fin.index <- rank_average_treatment_effect(
  cf,
  -1 * X$financial.autonomy.index, # Multiply by -1 to order by decreasing index
  subset = !is.na(X$financial.autonomy.index) # Ignore missing X-values
  )
plot(rate.fin.index, xlab = "Treated fraction", ylab = "Increase in test scores", main = "TOC: By increasing financial autonomy")

rate.fin.index
#>  estimate std.err             target
#>      0.69    0.22 priorities | AUTOC

TOC表明，财务自主指数较低的学生从该项目中获得的收益高于平均水平，并且 AUTOC 在常规水平上具有显著性：rate.fin.index$estimate / rate.fin.index$std.err = r rate.fin.index$estimate / rate.fin.index$std.err。与结果的标准差相比，即sd(Y) = r sd(Y)，这种收益也显得很有意义。

基于树的策略学习

在本节中，我们将介绍如何使用广义随机森林（GRF）的姐妹软件包policytree来找到基于树的治疗策略。由于相对平均处理效应（RATE）表明部分人群似乎从教育项目中受益较少，例如那些已经高度“经济自主”的学生，我们将尝试看看是否可以使用数据自适应算法根据子群体分配治疗。一种方法是假设一个简单且可解释的基于协变量的规则应该决定项目参与，这就是policytree所做的，通过找到一棵浅层决策树，使遵循这种治疗分配策略的经验“回报”最大化。

用$\pi (X_i)$表示一个函数（策略），该函数接收一个协变量向量$X_i$，并将其映射为一个关于对象是否应该接受治疗的二元决策： π ↦ { 0 , 1 } \pi\mapsto\{0,1\} π↦{0,1}（这可以很容易地扩展到多种治疗方法）。找到这样一个策略的任务被称为策略学习。给定经验“奖励分数”${\hat{\Gamma }}_i$，policytree找到一个基于树的策略$\pi (X_i)$，该策略最大化

$$\frac{1}{n}\sum _{i=1}^n(2\pi (X_i)-1){\hat{\Gamma }}_i.$$
（关于“2”的来源说明：因为π属于{0,1}，那么 2π - 1 属于{-1,1}，即当我们对单元 i 进行处理时，目标函数增加${\hat{\Gamma }}_i$，而当我们不对单元 i 进行处理时，目标函数减少$-{\hat{\Gamma }}_i$）。

下面我们将通过一个示例来介绍如何使用来自“policytree”的policy_tree函数来找到一个最优的深度为 2 的决策树策略。这个函数使用一个 C++求解器来找到一个浅层且最优的决策规则[^5]。我们正在使用单独的数据集来拟合和评估该策略。

library(policytree)
# Use train/evaluation school split from above, but use non-missing units for policy_tree
eval <- (1:nrow(X))[-train]
not.missing <- which(complete.cases(X))
train <- train[which(train %in% not.missing)]
eval <- eval[which(eval %in% not.missing)]

# Compute doubly robust scores
dr.scores <- get_scores(cf)
# Use as the ATE as a "cost" of program treatment to find something non-trivial
cost <- ate[["estimate"]]
dr.rewards <- cbind(control=-dr.scores, treat=dr.scores - cost)

# Fit depth 2 tree on training subset
tree <- policy_tree(X[train, ], dr.rewards[train, ], min.node.size = 100)
plot(tree, leaf.labels = c("dont treat", "treat"))

拟合规则显然可以区分那些从样本中的项目中受益高于平均水平的单位。为了评估这一点的统计有效性，我们应该在一个保留的数据集上对其进行评估，在这个数据集中，它不一定会给出相同的平均回报。

pi.hat <- predict(tree, X[eval,]) - 1
mean((dr.scores[eval] - cost) * (2*pi.hat - 1))
#> [1] -0.29

我们可以将平均处理效应（ATE）分解为树所隐含的子组，并查看保留样本的一些汇总统计信息，例如平均处理效应减去成本。

leaf.node <- predict(tree, X[eval, ], type = "node.id")
action.by.leaf <- unlist(lapply(split(pi.hat, leaf.node), unique))

# 定义一个函数来计算汇总统计信息
leaf_stats <- function(leaf) {
  c(ATE.minus.cost = mean(leaf), std.err = sd(leaf) / sqrt(length(leaf)), size = length(leaf))
}

cbind(
  rule = ifelse(action.by.leaf == 0, "dont treat", "treat"),
  aggregate(dr.scores[eval] - cost, by = list(leaf.node = leaf.node),
            FUN = leaf_stats)
)
#>         rule leaf.node x.ATE.minus.cost x.std.err  x.size
#> 2      treat         2            -0.23      0.43 4035.00
#> 4      treat         4            -0.89      0.63 1787.00
#> 5 dont treat         5            -3.26      1.82  238.00

深度为 2 的树可能要求比较高，如果我们只要求进行一次分割（根据单个协变量截止值进行处理/不处理），我们会得到：

tree.depth1 <- policy_tree(X[train, ], dr.rewards[train, ], depth = 1, min.node.size = 100)
pi.hat.eval <- predict(tree.depth1, X[eval, ]) - 1

treat.eval <- eval[pi.hat.eval == 1]
dont.treat.eval <- eval[pi.hat.eval == 0]

average_treatment_effect(cf, subset = treat.eval)
#> estimate  std.err 
#>      3.9      0.8
average_treatment_effect(cf, subset = dont.treat.eval)
#> estimate  std.err 
#>      1.8      2.3

plot(tree.depth1, leaf.labels = c("dont treat", "treat"))

案例：测量贫困对注意力的影响

在本节中，我们按照Farbmacher等人（2021）的研究进行一个示例分析，他们使用了来自Carvalho等人（2016）的数据研究因果森林应用。Carvalho等人（2016）进行了一项实验，他们随机分配低收入个体在发薪日之前（$W=1$）或之后（$W=0$）进行认知测试。结果是在一项旨在测量认知能力的测试中的表现。原始研究平均来看没有发现效果，然而，Farbmacher等人（2021 ）进行了异质性处理效应（HTE）分析，并发现有证据表明在部分人群中贫困会损害认知功能。此数据的处理副本存储在github 存储库中，包含来自大约 2500 个个体的观察结果以及 27 个特征，如年龄、收入等。教育程度被存储为有序值，高值意味着高教育水平，低值意味着低教育水平（4：大学毕业生，3：上过一些大学，2：高中毕业生，1：低于高中学历）。

数据概述

data <- read.csv("data/carvalho2016.csv")
# As outcomes we'll look at the number of correct answers.
Y <- data$outcome.num.correct.ans
W <- data$treatment
X <- data[-(1:4)]

这项研究据报道是以随机对照试验（RCT）的形式进行的，只是为了确保我们估计倾向得分，以验证我们可能不会无意中遗漏缺乏重叠的情况。

rf <- regression_forest(X, W, num.trees = 500)
p.hat <- predict(rf)$predictions

hist(p.hat)

rf <- regression_forest（X， W， num.trees = 500） p.hat <- predict（rf）$predictions hist（p.hat）

数据包含 2480 个观测值和 24 个协变量。相对于样本大小，在如此大量的协变量上拟合 CATE 估计量在异质性治疗效果（HTE）检测中可能效力不足，因此下面我们首先预测条件均值$E[Y_i|X_i]$，然后使用简单的森林变量重要性来选择在 CATE 估计步骤中保留哪些协变量。

Y.forest <- regression_forest(X, Y)
Y.hat <- predict(Y.forest)$predictions

varimp.Y <- variable_importance(Y.forest)

# 保留用于条件平均处理效应（CATE）估计的前 10 个变量。
keep <- colnames(X)[order(varimp.Y, decreasing = TRUE)[1:10]]
keep
#>  [1] "education"                         "black"                            
#>  [3] "white"                             "household.income"                 
#>  [5] "age"                               "disabled"                         
#>  [7] "current.income"                    "pay.day.amount.fraction.of.income"
#>  [9] "household.size"                    "widowed"

分析异质性TOC

X.cf <- X[, keep]
W.hat <- 0.5
# 将数据的前一半留作训练，后一半留作评估。（注意，结果可能会因我们为训练/评估保留的样本不同而有所变化）

train <- 1:(nrow(X.cf) / 2)

train.forest <- causal_forest(X.cf[train, ], Y[train], W[train], Y.hat = Y.hat[train], W.hat = W.hat)
tau.hat.eval <- predict(train.forest, X.cf[-train, ])$predictions

eval.forest <- causal_forest(X.cf[-train, ], Y[-train], W[-train], Y.hat = Y.hat[-train], W.hat = W.hat)

与上述研究一致，平均来看似乎没有影响。

average_treatment_effect(eval.forest)
#> estimate  std.err 
#>     0.15     0.60

varimp <- variable_importance(eval.forest)
ranked.vars <- order(varimp, decreasing = TRUE)
colnames(X.cf)[ranked.vars[1:5]]
#> [1] "age"              "current.income"   "education"        "household.income"
#> [5] "household.size"

结果是衡量认知能力测试中的正确答案数量，所以负的 CATE 意味着由于贫困导致的认知障碍，因此在计算 RATE（AUTOC）时，我们按照最负的 CATE 进行排序。我们也考虑年龄（从年长到年轻），因为它在分割频率中出现的频率很高。

rate.cate <- rank_average_treatment_effect(eval.forest, list(cate = -1 *tau.hat.eval))
rate.age <- rank_average_treatment_effect(eval.forest, list(age = X[-train, "age"]))

par(mfrow = c(1, 2))
plot(rate.cate, ylab = "Number of correct answers", main = "TOC: By most negative CATEs")
plot(rate.age, ylab = "Number of correct answers", main = "TOC: By decreasing age")

rate.cate
#>  estimate std.err       target
#>      -1.5    0.61 cate | AUTOC
rate.age
#>  estimate std.err      target
#>      -1.1    0.68 age | AUTOC

TOC在这里很有信息量，因为它似乎在指示一个较低的分位数$q$，在这个分位数处认知可能会下降。法布马赫等人（2021 年）认为，似乎有一小部分人口受到贫困的不利影响，在这种情况下，自动相关性系数（AUTOC）在检测异质性方面可能比所谓的基尼系数更强大。使用基尼加权进行相同的评估会得出较低的估计值。

qini.cate <- rank_average_treatment_effect(eval.forest, list(cate = -1 *tau.hat.eval), target = "QINI")
qini.age <- rank_average_treatment_effect(eval.forest, list(age = X[-train, "age"]), target = "QINI")

qini.cate
#>  estimate std.err      target
#>     -0.28    0.18 cate | QINI
qini.age
#>  estimate std.err     target
#>     -0.26    0.17 age | QINI

References

[1] Athey, Susan, Julie Tibshirani, and Stefan Wager. “Generalized random forests.” The Annals of Statistics 47, no. 2 (2019): 1148-1178.

[2] Breiman, Leo. “Random forests.” Machine learning 45, no. 1 (2001): 5-32.

[3] Bruhn, Miriam, Luciana de Souza Leão, Arianna Legovini, Rogelio Marchetti, and Bilal Zia. “The impact of high school financial education: Evidence from a large-scale evaluation in Brazil.” American Economic Journal: Applied Economics 8, no. 4 (2016).

[4] Carvalho, Leandro S., Stephan Meier, and Stephanie W. Wang. “Poverty and economic decision-making: Evidence from changes in financial resources at payday.” American Economic Review 106, no. 2 (2016): 260-84.

[5] Chernozhukov, Victor, Denis Chetverikov, Mert Demirer, Esther Duflo, Christian Hansen, Whitney Newey, and James Robins. “Double/debiased machine learning for treatment and structural parameters.” The Econometrics Journal, 2018.

[6] Efron, Bradley. “Prediction, estimation, and attribution.” International Statistical Review 88 (2020): S28-S59.

[7] Farbmacher, Helmut, Heinrich Kögel, and Martin Spindler. “Heterogeneous effects of poverty on attention.” Labour Economics 71 (2021): 102028.

[8] Imbens, Guido W., and Donald B. Rubin. Causal inference in statistics, social, and biomedical sciences. Cambridge University Press, 2015.

[9] Robins, James M., Andrea Rotnitzky, and Lue Ping Zhao. “Estimation of regression coefficients when some regressors are not always observed.” Journal of the American Statistical Association 89, no. 427 (1994): 846-866.

[10] Stone, Charles J. “Optimal rates of convergence for nonparametric estimators.” The Annals of Statistics (1980): 1348-1360.

[11] Nie, Xinkun, and Stefan Wager. “Quasi-oracle estimation of heterogeneous treatment effects.” Biometrika 108, no. 2 (2021): 299-319.

[12] Robinson, Peter M. “Root-N-consistent semiparametric regression.” Econometrica: Journal of the Econometric Society (1988): 931-954.

[13] Zheng, Wenjing, and Mark J. van der Laan. “Cross-validated targeted minimum-loss-based estimation.” In Targeted Learning, pp. 459-474. Springer, New York, NY, 2011.

[14] Wager, Stefan, and Susan Athey. “Estimation and inference of heterogeneous treatment effects using random forests.” Journal of the American Statistical Association 113.523 (2018): 1228-1242.

[15] Yadlowsky, Steve, Scott Fleming, Nigam Shah, Emma Brunskill, and Stefan Wager. “Evaluating Treatment Prioritization Rules via Rank-Weighted Average Treatment Effects.” arXiv preprint arXiv:2111.07966 (2021).

[16] Zeileis, Achim, Torsten Hothorn, and Kurt Hornik. “Model-based recursive partitioning.” Journal of Computational and Graphical Statistics 17, no. 2 (2008): 492-514.