文章目录
- Ch7.微分方程
- 题型:微分方程求解、综合题、应用题
- 一、常微分方程的基本概念
- 二、一阶微分方程(一阶变系数)
- 1.可分离变量
- 2.齐次微分方程
- 3.一阶线性微分方程: y ′ + P ( x ) y = Q ( x ) y'+P(x)y=Q(x) y′+P(x)y=Q(x)
- 4.伯努利方程: y ′ + P ( x ) y = Q ( x ) y n ( n ≠ 0 , 1 ) y'+P(x)y=Q(x)y^n \quad (n≠0,1) y′+P(x)y=Q(x)yn(n=0,1)
- 5.全微分方程: P ( x , y ) d x + Q ( x , y ) d y = 0 P(x,y)dx+Q(x,y)dy=0 P(x,y)dx+Q(x,y)dy=0,且 Q x = P y Q_x=P_y Qx=Py
- 三、可降阶的高阶方程:可降阶的微分方程(二阶变系数)
- 四、高阶线性微分方程
- 五、微分方程综合题
Ch7.微分方程

题型:微分方程求解、综合题、应用题

一、常微分方程的基本概念
1.常微分方程的基本概念
微分方程的阶:未知函数的最高阶导数的阶数

2.求解微分方程的方法:微分算子法
1.待定系数法:计算量大
2.拉普拉斯变换:较难
3.微分算子法:计算量小

二、一阶微分方程(一阶变系数)
一阶微分方程的一般形式: d y d x = f ( x , y ) \dfrac{dy}{dx}=f(x,y) dxdy=f(x,y)
1.可分离变量
y ′ = f ( x ) g ( y ) ⇨ d y d x = f ( x ) g ( y ) ⇨ d y g ( y ) = f ( x ) d x y'=f(x)g(y) \quad ⇨ \quad \dfrac{dy}{dx}=f(x)g(y) \quad ⇨ \quad \dfrac{dy}{g(y)}=f(x)dx y′=f(x)g(y)⇨dxdy=f(x)g(y)⇨g(y)dy=f(x)dx
或能表示为 g ( y ) d y = f ( x ) d x g(y)dy=f(x)dx g(y)dy=f(x)dx的方程,称为可分离变量的方程
例题1:06年2.
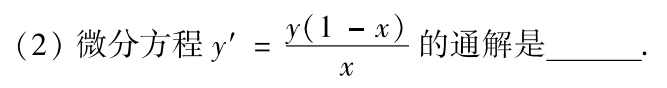
分析:变量可分离
答案: y = C x e − x ( C 为任意常数 ) y=Cxe^{-x}(C为任意常数) y=Cxe−x(C为任意常数) 写微分方程的通解,要注意对C声明:C为任意常数。在填空和大题步骤里要注意!
例题2:19年10. 变量可分离:一阶非线性
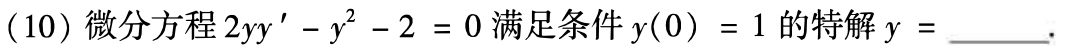
分析:非线性微分方程,注意区分是一阶还是二阶。
一阶非线性:变量可分离
二阶非线性:可降阶
答案: y = 3 e x − 2 y=\sqrt{3e^x-2} y=3ex−2
2.齐次微分方程
齐次方程: d y d x = f ( y x ) \dfrac{dy}{dx}=f(\dfrac{y}{x}) dxdy=f(xy)
求解方法:化为可分离变量,令 u = y x u=\dfrac{y}{x} u=xy,则 y = x u y=xu y=xu, d y d x = u + x d u d x \dfrac{dy}{dx}=u+x\dfrac{du}{dx} dxdy=u+xdxdu
例题1:14年11.
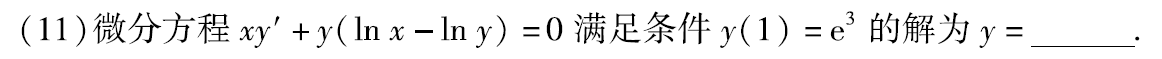
分析:
易错点:ln(lnu-1)=lnx+C。两边取对数应该得到 lnu-1=Cx,而不是x+c,不要错把答案写成 y=x·ex+2

答案:
x
⋅
e
2
x
+
1
x·e^{2x+1}
x⋅e2x+1
3.一阶线性微分方程: y ′ + P ( x ) y = Q ( x ) y'+P(x)y=Q(x) y′+P(x)y=Q(x)
y和y’都是一次,则为线性
①一阶齐次 (Q(x)=0)
y = C ⋅ e − ∫ P ( x ) d x y=C·e^{-\int P(x)dx} y=C⋅e−∫P(x)dx
②一阶非齐次 (Q(x)≠0)
y = e − ∫ P ( x ) d x ( ∫ Q ( x ) e ∫ P ( x ) d x d x + C ) y=e^{-\int P(x)dx}(\int Q(x)e^{\int P(x)dx}dx+C) y=e−∫P(x)dx(∫Q(x)e∫P(x)dxdx+C)
例题1:11年10.

答案:
e
−
x
⋅
s
i
n
x
e^{-x}·sinx
e−x⋅sinx
例题2:
d
x
d
y
\dfrac{dx}{dy}
dydx

分析:
法1:化出
d
y
d
x
\dfrac{dy}{dx}
dxdy,发现什么类型都不是。考虑x,y对调。化出
d
x
d
y
\dfrac{dx}{dy}
dydx
法2:凑成 全微分方程

4.伯努利方程: y ′ + P ( x ) y = Q ( x ) y n ( n ≠ 0 , 1 ) y'+P(x)y=Q(x)y^n \quad (n≠0,1) y′+P(x)y=Q(x)yn(n=0,1)
求解步骤: u = y 1 − n u=y^{1-n} u=y1−n
注:
(1)n≠0,1:若n为0,则变为一阶线性。若n为1,则变为可分离变量
(2)求解步骤:
两边同时除以
y
n
y^n
yn得:
y
−
n
d
y
d
x
+
P
(
x
)
y
1
−
n
=
Q
(
x
)
y^{-n}\dfrac{dy}{dx}+P(x)y^{1-n}=Q(x)
y−ndxdy+P(x)y1−n=Q(x)
可以看出, d ( y 1 − n ) d x = ( 1 − n ) y − n d y d x \dfrac{d(y^{1-n})}{dx}=(1-n)y^{-n}\dfrac{dy}{dx} dxd(y1−n)=(1−n)y−ndxdy,左边项只差 ( 1 − n ) (1-n) (1−n)。
两边同乘 ( 1 − n ) (1-n) (1−n),得: ( 1 − n ) y − n d y d x + ( 1 − n ) P ( x ) y 1 − n = ( 1 − n ) Q ( x ) (1-n)y^{-n}\dfrac{dy}{dx}+(1-n)P(x)y^{1-n}=(1-n)Q(x) (1−n)y−ndxdy+(1−n)P(x)y1−n=(1−n)Q(x)
令 u = y 1 − n u=y^{1-n} u=y1−n,得: d u d x + ( 1 − n ) P ( x ) u = ( 1 − n ) Q ( x ) \dfrac{du}{dx}+(1-n)P(x)u=(1-n)Q(x) dxdu+(1−n)P(x)u=(1−n)Q(x)
再用一阶非齐次微分方程 公式即可求解伯努利方程
u
=
e
−
∫
(
1
−
n
)
P
(
x
)
d
x
(
∫
(
1
−
n
)
Q
(
x
)
e
∫
(
1
−
n
)
P
(
x
)
d
x
d
x
+
C
)
=
y
1
−
n
u=e^{-\int (1-n)P(x)dx}(\int (1-n)Q(x)e^{\int (1-n)P(x)dx}dx+C)=y^{1-n}
u=e−∫(1−n)P(x)dx(∫(1−n)Q(x)e∫(1−n)P(x)dxdx+C)=y1−n,解得
y
y
y
5.全微分方程: P ( x , y ) d x + Q ( x , y ) d y = 0 P(x,y)dx+Q(x,y)dy=0 P(x,y)dx+Q(x,y)dy=0,且 Q x = P y Q_x=P_y Qx=Py
1.定义:如果 d u ( x , y ) = P ( x , y ) d x + Q ( x , y ) d y du(x,y)=P(x,y)dx+Q(x,y)dy du(x,y)=P(x,y)dx+Q(x,y)dy,即右端是某个函数 u ( x , y ) u(x,y) u(x,y)的全微分,则称 P ( x , y ) d x + Q ( x , y ) d y = 0 P(x,y)dx+Q(x,y)dy=0 P(x,y)dx+Q(x,y)dy=0 为全微分方程。
2.判断标准
∂
P
(
x
,
y
)
∂
y
=
∂
Q
(
x
,
y
)
∂
x
\dfrac{∂P(x,y)}{∂y}=\dfrac{∂Q(x,y)}{∂x}
∂y∂P(x,y)=∂x∂Q(x,y)
3.求解方法:
(1)偏积分
(2)凑微分
(3)线积分
线积分公式:(积分与路径无关)
4.通解形式:
u
(
x
,
y
)
=
C
u(x,y)=C
u(x,y)=C
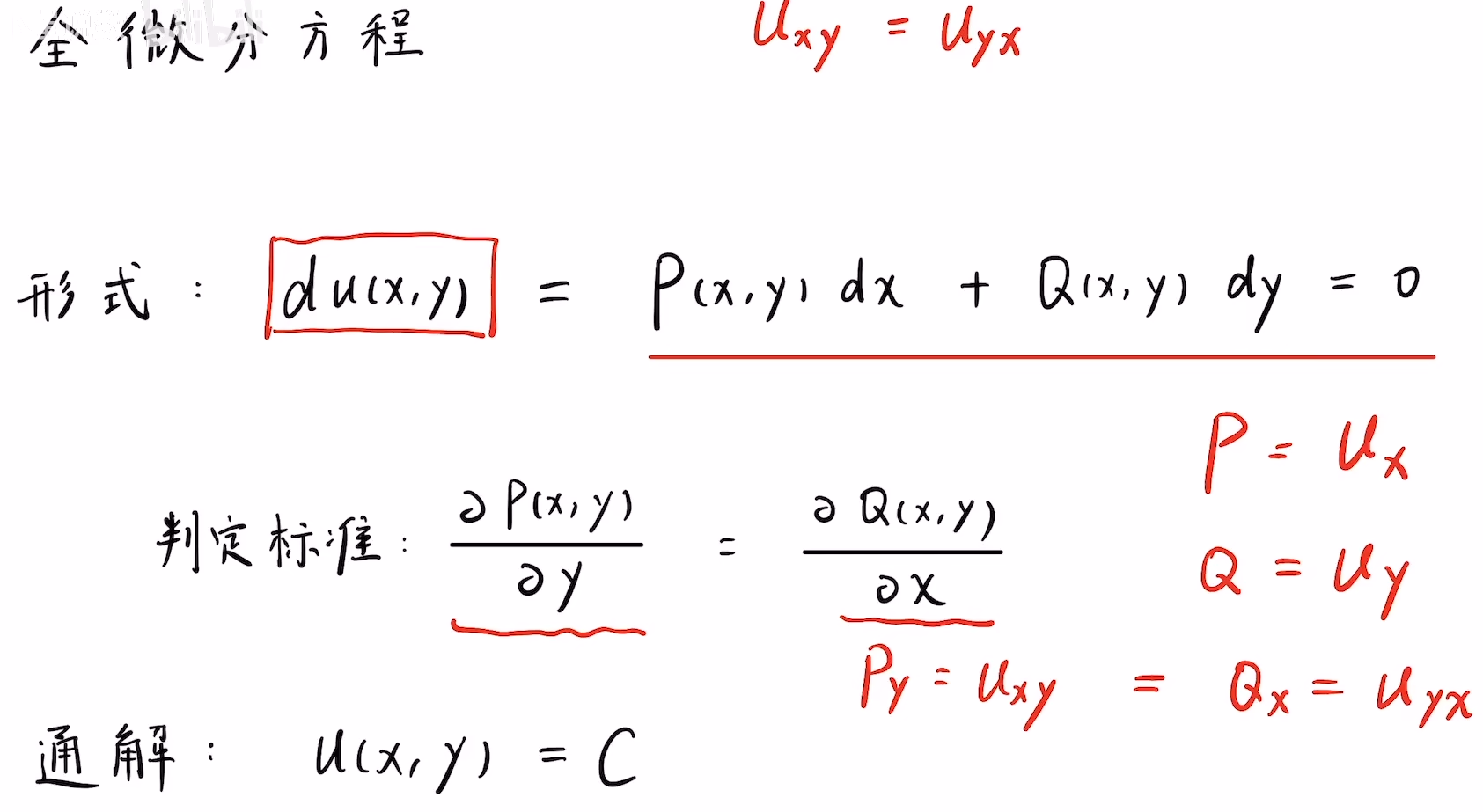
例题1:
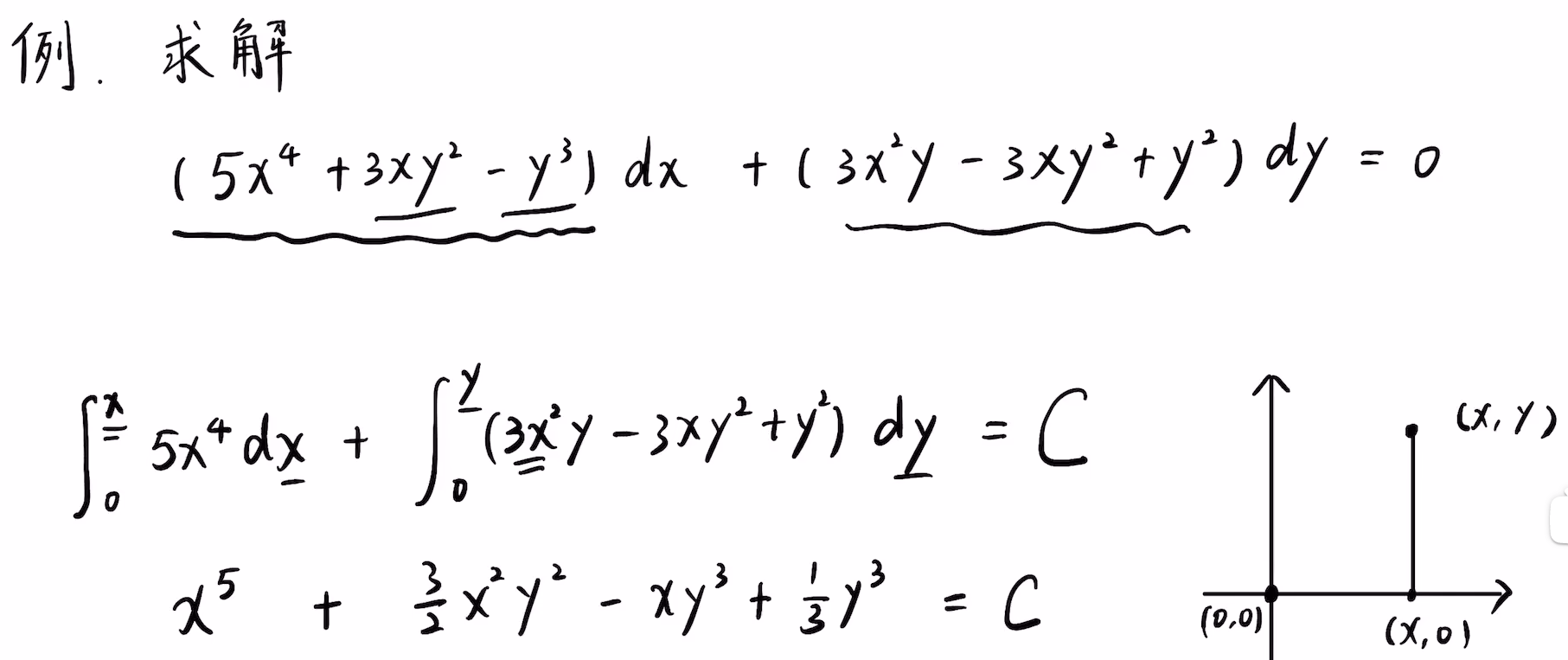
例题2:24李林880 第七章 基础题 填空(5)
注
若给定的一阶微分方程不属于上述五种标准形式,则:
①将x,y对调,变为x(y)
②利用简单的变量代换
三、可降阶的高阶方程:可降阶的微分方程(二阶变系数)
二阶微分方程的一般形式: y ′ ′ = f ( x , y , y ′ ) y''=f(x,y,y') y′′=f(x,y,y′)
1. y ( n ) = f ( x ) y^{(n)}=f(x) y(n)=f(x): y ′ ′ = f ( x ) y''=f(x) y′′=f(x) 只含x
累次积分
2. y ′ ′ = f ( x , y ′ ) y''=f(x,y') y′′=f(x,y′) 不显含y
令 y ′ = p , y ′ ′ = d p d x y'=p\ ,\ y''=\dfrac{dp}{dx} y′=p , y′′=dxdp,原式化为一阶微分方程 d p d x = f ( x , p ) \dfrac{dp}{dx}=f(x,p) dxdp=f(x,p)
y ′ = d y d x = p ( x ) , y ′ ′ = p ′ = d p d x y'=\dfrac{dy}{dx}=p(x)\ , \ y''=p'=\dfrac{dp}{dx} y′=dxdy=p(x) , y′′=p′=dxdp
3. y ′ ′ = f ( y , y ′ ) y''=f(y,y') y′′=f(y,y′) 不显含x
令 y ′ = p , y ′ ′ = p d p d y y'=p\ ,\ y''=p\dfrac{dp}{dy} y′=p , y′′=pdydp
y ′ = d y d x = p , y ′ ′ = d p d x = d p d y ⋅ d y d x = p ⋅ d p d y y'=\dfrac{dy}{dx}=p \ , \ y''=\dfrac{dp}{dx}=\dfrac{dp}{dy}·\dfrac{dy}{dx}=p·\dfrac{dp}{dy} y′=dxdy=p , y′′=dxdp=dydp⋅dxdy=p⋅dydp
例题1:02年3.
y
′
′
=
f
(
y
,
y
′
)
y''=f(y,y')
y′′=f(y,y′) 不显含x

分析:高阶定系数,出来一个定一个。不要最后统一定

答案: y = x + 1 y=\sqrt{x+1} y=x+1
例题2:23李林六套卷(四)13.
y
′
′
=
f
(
y
,
y
′
)
y''=f(y,y')
y′′=f(y,y′) 不显含x

分析:
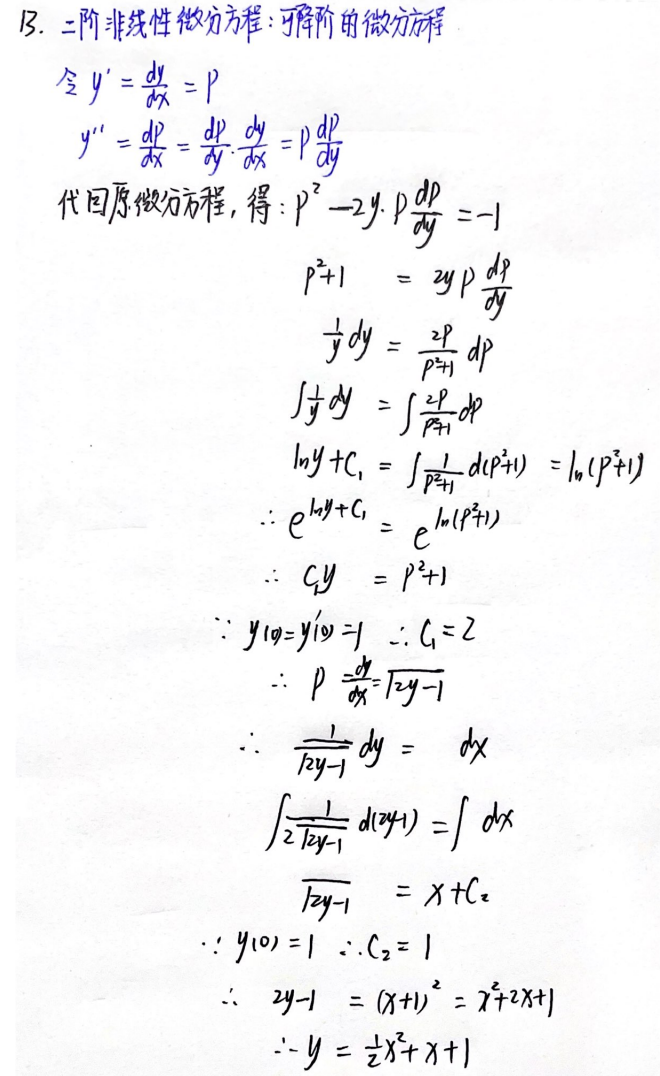
答案:
y
=
1
2
x
2
+
x
+
1
y=\dfrac{1}{2}x^2+x+1
y=21x2+x+1
四、高阶线性微分方程
1.线性微分方程 解的结构:4个定理
二阶线性微分方程的一般形式:
y
′
′
+
p
(
x
)
y
′
+
q
(
x
)
y
=
f
(
x
)
y''+p(x)y'+q(x)y=f(x)
y′′+p(x)y′+q(x)y=f(x)
若
f
(
x
)
≡
0
f(x)≡0
f(x)≡0,称为二阶线性齐次方程。否则称为二阶线性非齐次方程。
二阶线性齐次方程 : y ′ ′ + p ( x ) y ′ + q ( x ) y = 0 y''+p(x)y'+q(x)y=0 y′′+p(x)y′+q(x)y=0
二阶线性非齐次方程: y ′ ′ + p ( x ) y ′ + q ( x ) y = f ( x ) y''+p(x)y'+q(x)y=f(x) y′′+p(x)y′+q(x)y=f(x)
定理1:若
y
1
(
x
)
,
y
2
(
x
)
y_1(x),y_2(x)
y1(x),y2(x) 是 二阶齐次方程 的 两个线性无关的特解,则二阶齐次的通解为
y
=
C
1
y
1
(
x
)
+
C
2
y
2
(
x
)
y=C_1y_1(x)+C_2y_2(x)
y=C1y1(x)+C2y2(x)
【若为三阶方程,则通解要找3个线性无关的特解。若为n阶方程,则通解要找n个线性无关的特解】
定理2:非齐次通解 = 齐次通解 + 非齐次特解,即 y = Y + y ∗ y=Y+y^* y=Y+y∗
一阶非齐次通解:1个齐次解+特解
二阶非齐次通解:2个齐次解+特解,
y
=
C
1
y
1
(
x
)
+
C
2
y
2
(
x
)
+
y
∗
y=C_1y_1(x)+C_2y_2(x)+y^*
y=C1y1(x)+C2y2(x)+y∗
三阶非齐次通解:3个齐次解+特解
n 阶非齐次通解:n 个齐次解+特解

定理3:非齐次的两个特解之差,是齐次的解:
若
y
1
∗
(
x
)
,
y
2
∗
(
x
)
y_1^*(x),y_2^*(x)
y1∗(x),y2∗(x)均为非齐次线性微分方程的解,则
y
1
−
y
2
y_1-y_2
y1−y2为齐次解

定理4:非齐次解的叠加性
y
1
+
y
2
2
\dfrac{y_1+y_2}{2}
2y1+y2为非齐次的解
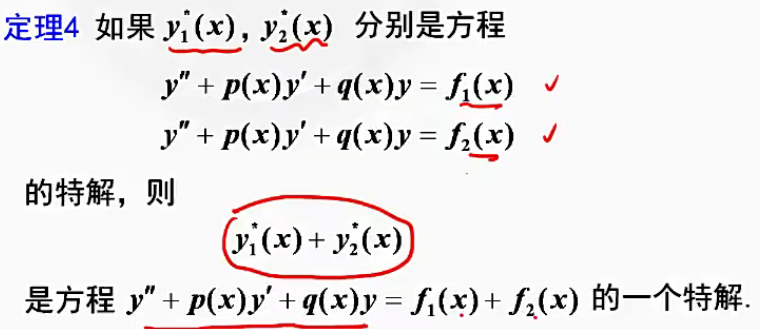
例题1:线性常系数,知道解 找方程
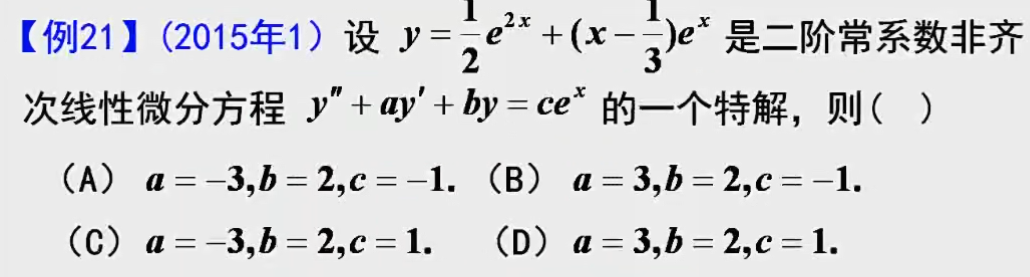
分析:非齐次的解 → 齐次的两个线性无关解、非齐次简单的特解 → 齐次的特征方程 → 齐次方程 → 非齐次的通解

例题2:16年3.
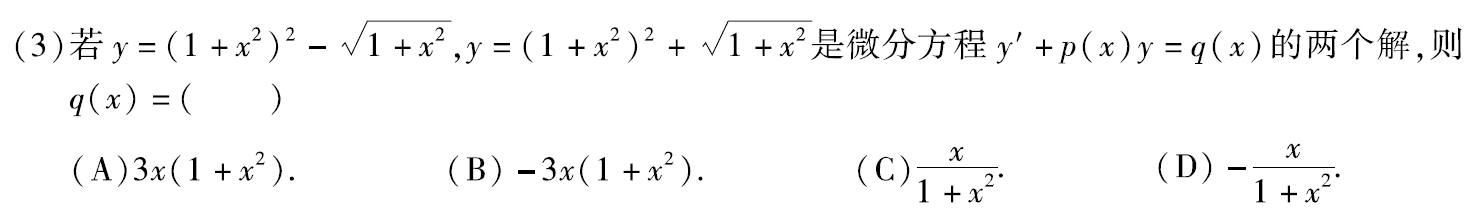
分析:

答案:A
例题3:13年10. 二阶非齐次通解:两个齐次通解 + 1个非齐次特解
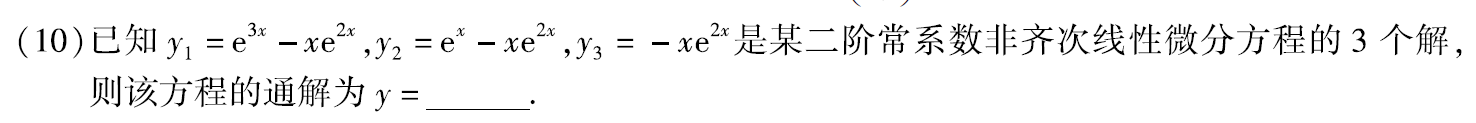
分析:

二阶通解:2个齐次解+特解
齐次解1:
y
=
y
2
−
y
3
=
e
x
y=y_2-y_3=e^x
y=y2−y3=ex
齐次解2:
y
=
y
1
−
y
3
=
e
3
x
y=y_1-y_3=e^{3x}
y=y1−y3=e3x
特解:
y
3
=
−
x
e
2
x
y_3=-xe^{2x}
y3=−xe2x
二阶通解:
C
1
e
x
+
C
2
e
3
x
−
x
e
2
x
C_1e^x+C_2e^{3x}-xe^{2x}
C1ex+C2e3x−xe2x (C₁,C₂为任意常数)
答案: C 1 e x + C 2 e 3 x − x e 2 x C_1e^x+C_2e^{3x}-xe^{2x} C1ex+C2e3x−xe2x (C₁,C₂为任意常数)
2.二阶线性常系数齐次微分方程: y ′ ′ + p y ′ + q y = 0 y''+py'+qy=0 y′′+py′+qy=0
1.特征方程: r 2 + p r + q = 0 r^2+pr+q=0 r2+pr+q=0
二阶常系数线性微分方程找通解的问题,可以归结为,特征方程找特征根的问题
①二阶齐次通解: y = C 1 y 1 ( x ) + C 2 y 2 ( x ) y=C_1y_1(x)+C_2y_2(x) y=C1y1(x)+C2y2(x), (C₁,C₂为任意常数)
②四阶齐次通解: y = C 1 y 1 ( x ) + C 2 y 2 ( x ) + C 3 y 3 ( x ) + C 4 y 4 ( x ) y=C_1y_1(x)+C_2y_2(x)+C_3y_3(x)+C_4y_4(x) y=C1y1(x)+C2y2(x)+C3y3(x)+C4y4(x), (C₁,C₂,C₃,C₄为任意常数)
2.求通解步骤:
①写出特征方程
r
2
+
p
r
+
q
=
0
r^2+pr+q=0
r2+pr+q=0 ,求出 两个特征根
r
1
r₁
r1和
r
2
r₂
r2
②根据特征根是不等实根、相等实根、共轭复根,写出微分方程的通解
| 两个特征根 r 1 , r 2 r_1,r_2 r1,r2 | 微分方程 y ′ ′ + p y + q = 0 y''+py+q=0 y′′+py+q=0的通解 | 特征根对应的通解项 y 1 ( x ) y_1(x) y1(x)、 y 2 ( x ) y_2(x) y2(x) |
|---|---|---|
| (1)不等实根: r 1 ≠ r 2 r_1≠r_2 r1=r2 | y = C 1 e r 1 x + C 2 e r 2 x y=C_1e^{r₁x}+C_2e^{r₂x} y=C1er1x+C2er2x | e r 1 x 、 e r 2 x e^{r_1x}、e^{r_2x} er1x、er2x |
| (2)相等实根: r 1 = r 2 = r r_1=r_2=r r1=r2=r | y = ( C 1 + C 2 x ) e r x y=(C_1+C_2x)e^{rx} y=(C1+C2x)erx | e r x 、 x e r x e^{rx}、xe^{rx} erx、xerx |
| (3)共轭复根: r 1 , 2 = α ± β i r_{1,2}=α±βi r1,2=α±βi | y = e α x ( C 1 cos β x + C 2 sin β x ) y=e^{αx}(C_1\cosβx+C_2\sinβx) y=eαx(C1cosβx+C2sinβx) | e α x cos β x 、 e α x sin β x e^{αx}\cosβx、e^{αx}\sinβx eαxcosβx、eαxsinβx |
例题1:17年10.
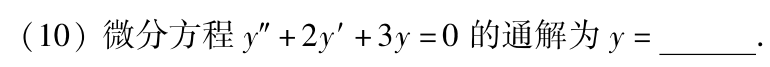
答案: e − x ( C 1 cos 2 x + C 2 sin 2 x ) ( C 1 , C 2 为任意常数) e^{-x}(C_1\cos\sqrt{2}x+C_2\sin\sqrt{2}x)(C_1,C_2为任意常数) e−x(C1cos2x+C2sin2x)(C1,C2为任意常数)
例题2:12年9.
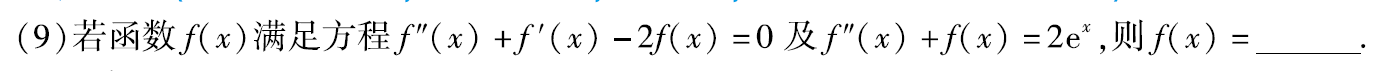
分析:给一个二阶,能求出通解。将通解代入第二个二阶,就能确定两个C的取值,从而求出特解。
解第一个二阶线性微分方程,得通解
y
=
C
1
e
−
2
x
+
C
2
e
x
y=C_1e^{-2x}+C_2e^x
y=C1e−2x+C2ex
求得
y
′
,
y
′
′
y',y''
y′,y′′,代入第二个二阶,解得系数
C
1
=
0
,
C
2
=
1
C_1=0,C_2=1
C1=0,C2=1
将系数代入通解,则特解为
y
=
e
x
y=e^x
y=ex
答案: e x e^x ex
例题3:2010年数二 :三阶常系数齐次 :通解项的结论,推广至更高阶同样适用

例题4:01年1. 由微分方程的解,还原微分方程

分析:

答案:
y
′
′
−
2
y
′
+
2
y
=
0
y''-2y'+2y=0
y′′−2y′+2y=0
3.二阶线性常系数非齐次微分方程: y ′ ′ + p y ′ + q y = f ( x ) y''+py'+qy=f(x) y′′+py′+qy=f(x)
二阶非齐次通解: y = C 1 y 1 ( x ) + C 2 y 2 ( x ) + y ∗ ( x ) y=C_1y_1(x)+C_2y_2(x)+y^*(x) y=C1y1(x)+C2y2(x)+y∗(x)

① f ( x ) = P m ( x ) e λ x f(x)=P_m(x)e^{λx} f(x)=Pm(x)eλx
1.求解二阶非齐次步骤:
(1)求齐次通解:写出齐次的特征方程,求出齐次的通解
(2)求非齐次特解:
设特解为
y
∗
=
x
k
Q
m
(
x
)
e
λ
x
y^*=x^kQ_m(x)e^{λx}
y∗=xkQm(x)eλx。确定k,照抄λ,待定
Q
m
(
x
)
Q_m(x)
Qm(x)。确定特解y*
令
y
∗
=
x
k
Q
m
(
x
)
e
λ
x
y*=x^kQ_m(x)e^{λx}
y∗=xkQm(x)eλx,
k
=
{
0
,
λ
不是特征方程的根
1
,
λ
是特征方程的单根
2
,
λ
是特征方程的重根
k=\left\{\begin{aligned} 0 & \quad ,λ不是特征方程的根 \\ 1 & \quad ,λ是特征方程的单根 \\ 2 & \quad ,λ是特征方程的重根 \end{aligned}\right.
k=⎩
⎨
⎧012,λ不是特征方程的根,λ是特征方程的单根,λ是特征方程的重根
(3)根据解的结构: y = Y + y ∗ y=Y+y^* y=Y+y∗
例题1:

例题2:

例题3:10年15. 二阶非齐次微分方程的通解的解结构:y=Y+y*
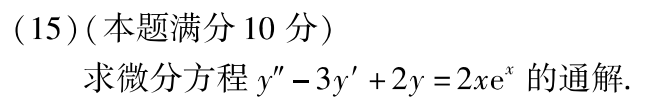
答案:
例题4:09年10.
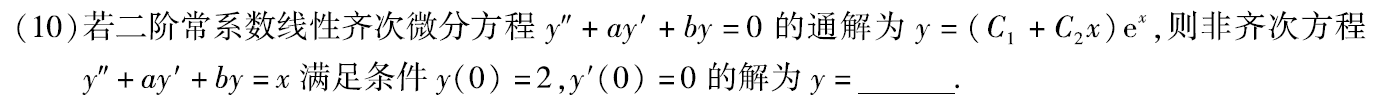
分析:
由齐次的通解
y
=
(
C
1
+
C
2
x
)
e
x
y=(C_1+C_2x)e^x
y=(C1+C2x)ex知,
λ
1
=
λ
2
=
1
λ_1=λ_2=1
λ1=λ2=1
则特征方程为
(
λ
−
1
)
2
=
λ
2
−
2
λ
+
1
=
0
∴
a
=
−
2
,
b
=
1
(λ-1)^2=λ^2-2λ+1=0 \quad ∴a=-2,b=1
(λ−1)2=λ2−2λ+1=0∴a=−2,b=1
∴二阶非齐次方程为
y
′
′
−
2
y
′
+
y
=
x
y''-2y'+y=x
y′′−2y′+y=x
属于(Ⅰ)型,设特解
y
∗
=
c
x
+
d
y*=cx+d
y∗=cx+d,则
y
∗
′
=
c
,
y
∗
′
′
=
0
y*'=c,y*''=0
y∗′=c,y∗′′=0
代入原二阶非齐次微分方程,得
−
2
c
+
c
x
+
d
=
x
-2c+cx+d=x
−2c+cx+d=x,
{
−
2
c
+
d
=
0
c
=
1
\left\{\begin{aligned} -2c+d=0 \\ c=1 \end{aligned}\right.
{−2c+d=0c=1 解得
{
c
=
1
d
=
2
∴
y
∗
=
x
+
2
\left\{\begin{aligned} c=1\\ d=2 \end{aligned}\right. \quad∴y*=x+2
{c=1d=2∴y∗=x+2
∴非齐次的通解=齐次通解+非齐次特解=
y
=
(
C
1
+
C
2
x
)
e
x
+
x
+
2
y=(C_1+C_2x)e^x+x+2
y=(C1+C2x)ex+x+2
代入初始条件
y
(
0
)
=
2
,
y
′
(
0
)
=
0
y(0)=2,y'(0)=0
y(0)=2,y′(0)=0 得
{
C
1
=
0
C
2
=
−
1
\left\{\begin{aligned} C_1= \quad0 \\ C_2=-1 \end{aligned}\right.
{C1=0C2=−1
∴符合初始条件的解为
y
=
−
x
e
x
+
x
+
2
y=-xe^x+x+2
y=−xex+x+2
答案: y = − x e x + x + 2 y=-xe^x+x+2 y=−xex+x+2
② f ( x ) = e α x [ P l ( x ) cos β x + P n ( x ) sin β x ] f(x)=e^{αx}[P_l(x)\cosβx+P_n(x)\sinβx] f(x)=eαx[Pl(x)cosβx+Pn(x)sinβx]
(1)求特解
令
y
∗
=
x
k
e
α
x
[
R
m
(
x
)
cos
β
x
+
R
m
(
x
)
sin
β
x
]
y^*=x^ke^{αx}[R_m(x)\cosβx+R_m(x)\sinβx]
y∗=xkeαx[Rm(x)cosβx+Rm(x)sinβx]
m = max { l , n } m=\max\{l,n\} m=max{l,n}
k = { 0 , α ± i β 不是特征方程的根 1 , α ± i β 是特征方程的单根 k=\left\{\begin{aligned} 0 & \quad ,α±iβ不是特征方程的根 \\ 1 & \quad ,α±iβ是特征方程的单根 \end{aligned}\right. k={01,α±iβ不是特征方程的根,α±iβ是特征方程的单根
例题1:高数辅导讲义P136例3(3)

分析:
解的叠加性,
f
1
(
x
)
=
x
2
+
1
f_1(x)=x^2+1
f1(x)=x2+1。
f
2
(
x
)
=
sin
x
f_2(x)=\sin x
f2(x)=sinx,α=0,β=1
齐次特征方程:
r
2
+
1
=
0
r^2+1=0
r2+1=0,
r
1
,
2
=
0
±
i
r_{1,2}=0±i
r1,2=0±i,α=0,β=1
可设特解
y
1
∗
=
a
x
2
+
b
x
+
c
y_1^*=ax^2+bx+c
y1∗=ax2+bx+c,可设特解
y
2
∗
=
x
(
A
cos
x
+
B
sin
x
)
y_2^*=x(A\cos x+B\sin x)
y2∗=x(Acosx+Bsinx)
答案:D
例题2:2017年数二:解的叠加性

答案:C
4.欧拉方程
1.二阶欧拉方程: x 2 y ′ ′ + p x y ′ + q y = 0 x²y''+pxy'+qy=0 x2y′′+pxy′+qy=0 (线性变系数)(填空题)
2.求解方法:

例题1:04年4.
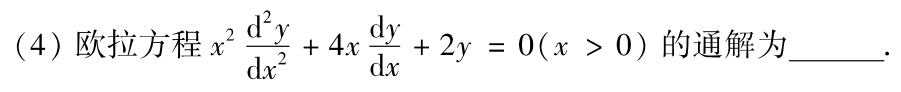
分析:
欧拉方程结论:
x
2
y
′
′
(
x
)
=
y
′
′
(
t
)
−
y
′
(
t
)
,
x
y
′
(
x
)
=
y
′
(
t
)
,
y
(
x
)
=
y
(
t
)
,
t
=
ln
x
x^2y''(x)=y''(t)-y'(t),xy'(x)=y'(t),y(x)=y(t),t=\ln x
x2y′′(x)=y′′(t)−y′(t),xy′(x)=y′(t),y(x)=y(t),t=lnx
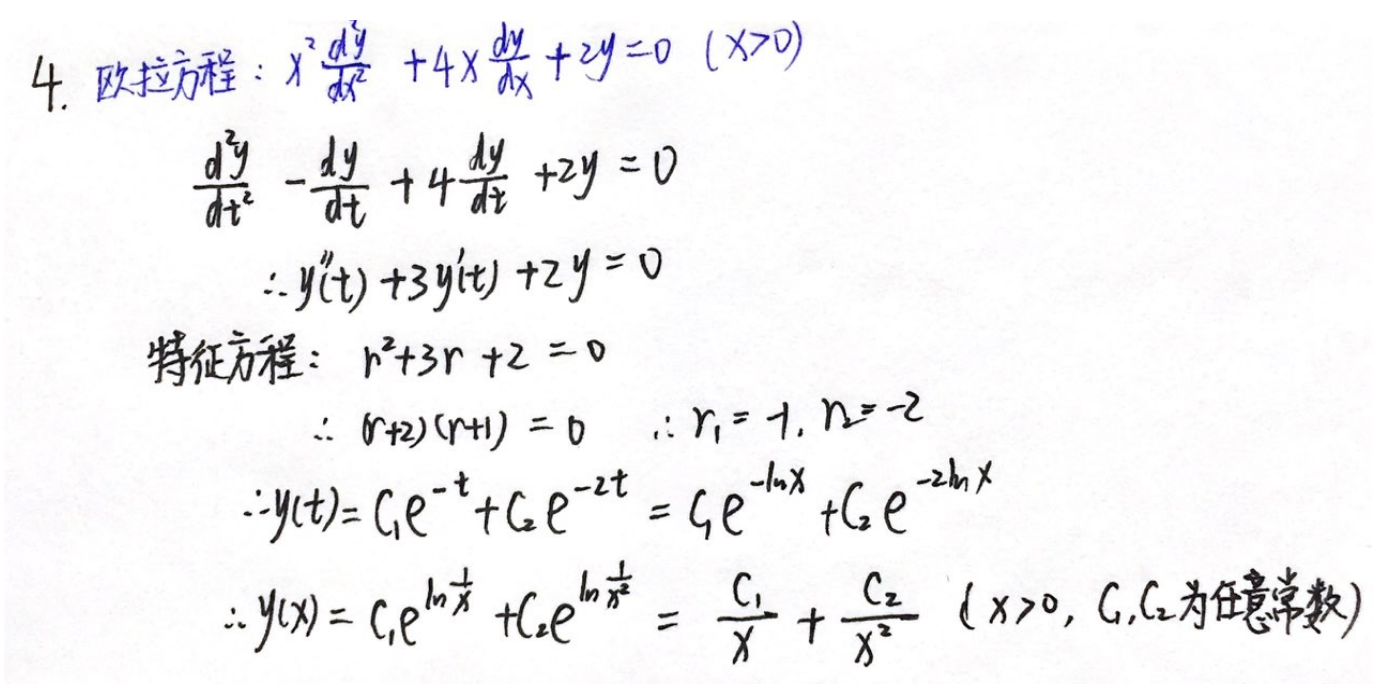
答案:
y
=
C
1
x
+
C
2
x
2
(
x
>
0
,
C
1
,
C
2
为任意常数
)
y=\dfrac{C_1}{x}+\dfrac{C_2}{x^2}(x>0,C_1,C_2为任意常数)
y=xC1+x2C2(x>0,C1,C2为任意常数)
例题2:21年13.
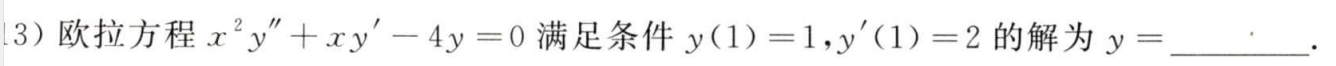
分析:

答案:
y
=
x
2
y=x²
y=x2
例题3:23李林六套卷(三)14.
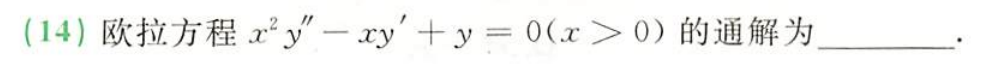
分析:

答案:
(
C
1
+
C
2
ln
x
)
x
(
x
>
0
,
C
1
C
2
为任意常数
)
(C₁+C₂\ln x)x \quad (x>0,C₁ C₂为任意常数)
(C1+C2lnx)x(x>0,C1C2为任意常数)
例题4:24李林六(四)12.

分析:
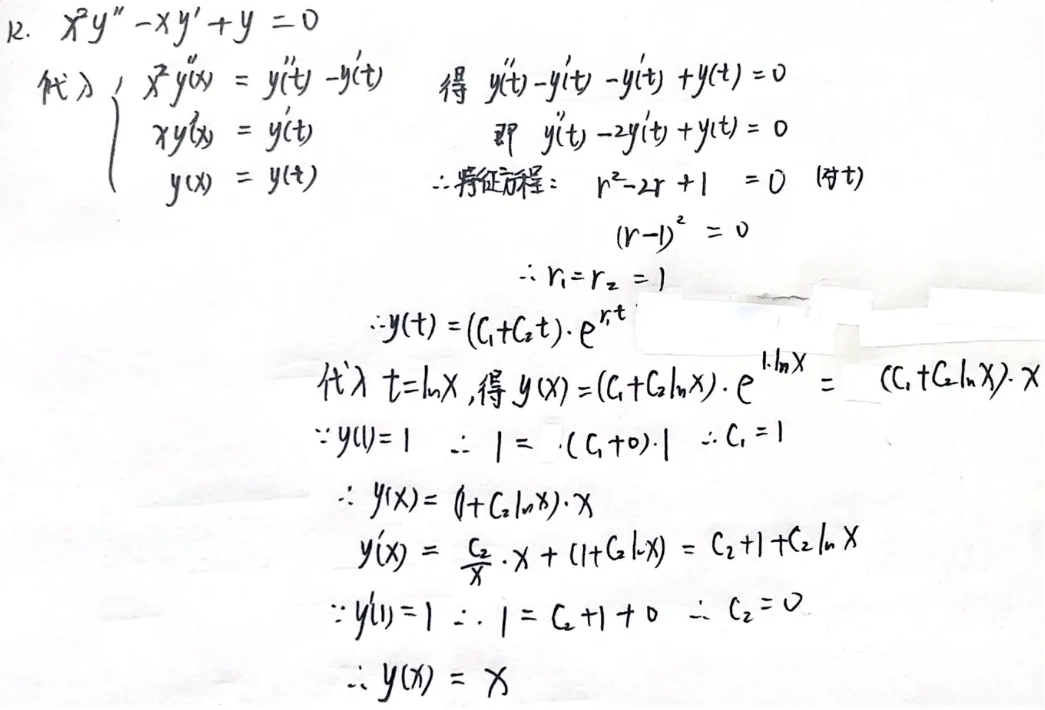
答案: x x x
五、微分方程综合题
1.微分方程的几何应用:切线斜率
例题1:23年17.(1)

2.无穷级数:构造微分方程求和函数
例题1:20年17.
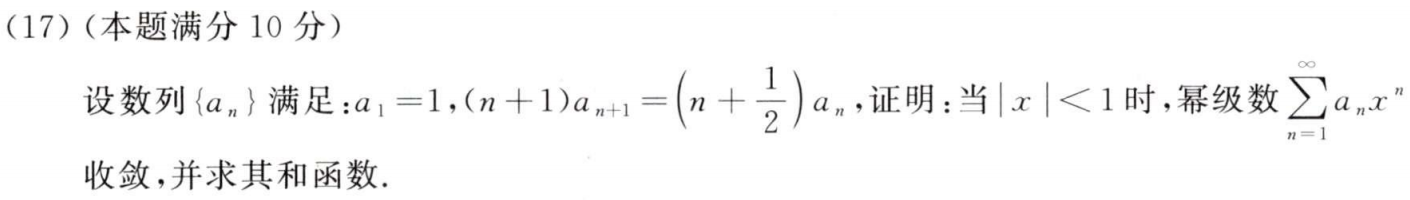
3.微分方程:取极限、广义积分
1.只要 y ( + ∞ ) y(+∞) y(+∞) 存在,则 y ′ ( + ∞ ) = 0 y'(+∞)=0 y′(+∞)=0。【水平渐近线】
例题1:20年11. 特征方程
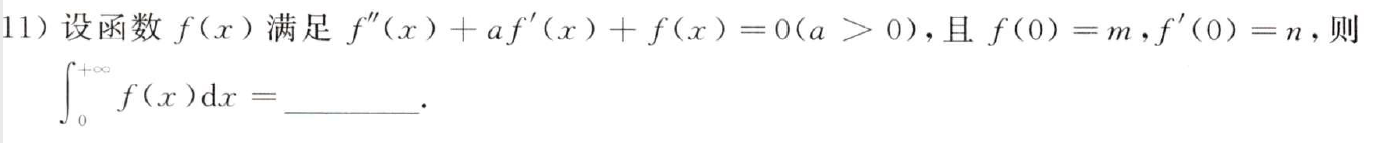
分析:Δ=a²-4,根据a的取值范围讨论解的形式,结果都能得到 f(+∞)=f’(+∞)=0

答案: n + a m n+am n+am
例题2:16年16. 二阶常系数线性微分方程 + 反常积分、用特征方程求二阶齐次微分方程的解

答案:

例题3:24李林四(三)11.
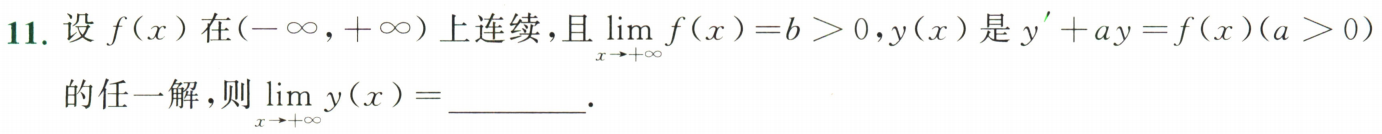
分析:只要
y
(
+
∞
)
y(+∞)
y(+∞) 存在,则
y
′
(
+
∞
)
=
0
y'(+∞)=0
y′(+∞)=0
lim
x
→
+
∞
f
(
x
)
=
b
\lim\limits_{x→+∞}f(x)=b
x→+∞limf(x)=b,
∴
y
=
b
∴y=b
∴y=b是f(x)的水平渐近线,则
y
′
(
+
∞
)
=
0
y'(+∞)=0
y′(+∞)=0
对微分方程
y
′
+
a
y
=
f
(
x
)
y'+ay=f(x)
y′+ay=f(x) 两边取极限,得
0
+
a
y
(
+
∞
)
=
b
0+ay(+∞)=b
0+ay(+∞)=b
∴
y
(
+
∞
)
=
b
a
∴y(+∞)=\dfrac{b}{a}
∴y(+∞)=ab
答案: b a \dfrac{b}{a} ab
























 1002
1002











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










