极限
数列极限
数列极限定义
设 { x n } \{x_n\} {xn} 为一个数列,若存在常数 a a a,对于给定的 ε > 0 \varepsilon > 0 ε>0,都存在 N ∈ Z + N \in \mathbb Z_+ N∈Z+,使 n > N n > N n>N 时,
∣ x n − a ∣ < ε |x_n-a|<\varepsilon ∣xn−a∣<ε
总成立,那么就称 a a a 为 { x n } \{x_n\} {xn} 的极限,或 { x n } \{x_n\} {xn} 收敛于 a a a,记为
lim n → ∞ x n = a \lim_{n\to\infty}x_n=a n→∞limxn=a
若不存在 a a a,则代表 { x n } \{x_n\} {xn} 没有极限,或 { x n } \{x_n\} {xn} 发散,也称 lim n → ∞ x n \lim\limits_{n\to\infty}x_n n→∞limxn 不存在。
数列极限运算
我们设 { a n } , { b n } \{a_n\},\{b_n\} {an},{bn} 满足 lim n → ∞ a n = A , lim n → ∞ b n = B \lim\limits_{n\to\infty}a_n=A,\lim\limits_{n\to\infty}b_n=B n→∞liman=A,n→∞limbn=B,则有。
lim
n
→
∞
(
a
n
±
b
n
)
=
A
±
B
\lim\limits_{n\to\infty}(a_n\pm b_n)=A\pm B
n→∞lim(an±bn)=A±B
lim
n
→
∞
(
a
n
b
n
)
=
A
B
\lim\limits_{n\to\infty}(a_nb_n)=AB
n→∞lim(anbn)=AB
lim
n
→
∞
(
a
n
b
n
)
=
A
B
(
B
≠
0
,
∀
b
i
,
b
i
≠
0
)
\lim\limits_{n\to\infty}(\frac{a_n}{b_n})=\frac{A}{B}(B\not=0,\forall b_i,bi\not=0)
n→∞lim(bnan)=BA(B=0,∀bi,bi=0)
常见数列极限
lim
n
→
∞
c
=
c
\lim\limits_{n\to\infty}c=c
n→∞limc=c(
c
c
c 为常数)
lim
n
→
∞
n
=
+
∞
\lim\limits_{n\to\infty}n=+\infty
n→∞limn=+∞(
c
c
c 为常数)
lim
n
→
∞
1
n
a
=
0
\lim\limits_{n\to\infty}\frac{1}{n^a}=0
n→∞limna1=0(
a
a
a 为常数,
a
>
0
a > 0
a>0)
lim
n
→
∞
a
n
=
0
\lim\limits_{n\to\infty}a^n=0
n→∞liman=0(
a
a
a 为常数,
0
<
a
<
1
0<a<1
0<a<1)
lim
n
→
∞
a
n
=
+
∞
\lim\limits_{n\to\infty}a^n=+\infty
n→∞liman=+∞(
a
a
a 为常数,
1
<
a
1<a
1<a)
夹极限法则:若数列
{
a
n
}
{
b
n
}
{
c
n
}
\{a_n\}\{b_n\}\{c_n\}
{an}{bn}{cn},满足
∀
0
≤
n
,
a
n
<
b
n
<
c
n
\forall 0\leq n,a_n<b_n<c_n
∀0≤n,an<bn<cn,且
lim
n
→
∞
a
n
=
lim
n
→
∞
c
n
=
t
\lim\limits_{n\to\infty}a_n=\lim\limits_{n\to\infty}c_n=t
n→∞liman=n→∞limcn=t, 则
lim
n
→
∞
b
n
=
t
\lim\limits_{n\to\infty} b_n=t
n→∞limbn=t。
结论
若 { x n } \{x_n\} {xn} 为单调数列,且 { x n } \{x_n\} {xn} 有界,则 lim n → ∞ x n \lim\limits_{n\to\infty}x_n n→∞limxn 存在。
若 { x n } \{x_n\} {xn} 无界,则 lim n → ∞ x n \lim\limits_{n\to\infty}x_n n→∞limxn 必不存在。
若 { x n } \{x_n\} {xn} 中,存在 { a n } \{a_n\} {an} 和 { b n } \{b_n\} {bn} 都为 { x n } \{x_n\} {xn} 子序列,且 lim n → ∞ a n ≠ lim n → ∞ b n \lim\limits_{n\to\infty}a_n\not=\lim\limits_{n\to\infty}b_n n→∞liman=n→∞limbn,则 lim n → ∞ x n \lim\limits_{n\to\infty}x_n n→∞limxn 必不存在。
若数列 { x n } \{x_n\} {xn} 收敛,则 { x n } \{x_n\} {xn} 极限唯一。
若数列 { x n } \{x_n\} {xn} 收敛,那么 { x n } \{x_n\} {xn} 有界。
若 lim n → ∞ x n = a \lim\limits_{n\to\infty}x_n=a n→∞limxn=a 且 a > 0 a>0 a>0,则存在 N ∈ Z + N \in \mathbb Z_+ N∈Z+,当 n > N n>N n>N 时,有 x n > 0 x_n>0 xn>0。
若 lim n → ∞ x n = a \lim\limits_{n\to\infty}x_n=a n→∞limxn=a 且 a < 0 a<0 a<0,则存在 N ∈ Z + N \in \mathbb Z_+ N∈Z+,当 n > N n>N n>N 时,有 x n < 0 x_n<0 xn<0。
若一数列收敛于 a a a,则其任意子序列收敛于 a a a。
函数极限
函数极限定义
若存在 r > 0 r>0 r>0 使得 D = { x ∣ 0 < ∣ x − x 0 ∣ < r , x ≠ x 0 } D=\{x|0<|x-x_0|<r,x\not=x_0\} D={x∣0<∣x−x0∣<r,x=x0} 包含于 f ( x ) f(x) f(x) 定义域,则说 y = f ( x ) y=f(x) y=f(x) 在 x 0 x_0 x0 附近有定义,称去心邻域内有定义。
若函数 f ( x ) f(x) f(x) 在 x 0 x_0 x0 处某去心邻域内有定义。若存在常数 A A A,对于任意 ε > 0 \varepsilon > 0 ε>0,总存在 δ > 0 \delta >0 δ>0,使得
∀ 0 < ∣ x − x 0 ∣ < δ , ∣ f ( x ) − A ∣ < δ \large{\forall} \normalsize 0<|x-x_0|<\delta,|f(x)-A|<\delta ∀0<∣x−x0∣<δ,∣f(x)−A∣<δ
那么常数 A A A 就叫函数 f ( x ) f(x) f(x) 当 x → x 0 x \to x_0 x→x0 时的极限,记作 lim x → x 0 f ( x ) = A \lim\limits_{x\to x_0}f(x)=A x→x0limf(x)=A。
函数 f ( x ) f(x) f(x) 在 x 0 x_0 x0 处极限与 f ( x 0 ) f(x_0) f(x0) 无关,例如: f ( x ) = { x 2 ( x ≠ 1 ) − 1024 ( x = 1 ) f(x)=\begin{cases}x^2(x\not=1)\\-1024(x=1)\end{cases} f(x)={x2(x=1)−1024(x=1) 此时, lim x → x 0 f ( x ) = x 2 = 1 \lim\limits_{x\to x_0}f(x)=x^2=1 x→x0limf(x)=x2=1,而不是 lim x → x 0 = f ( x 0 ) = − 1024 \lim\limits_{x\to x_0}=f(x_0)=-1024 x→x0lim=f(x0)=−1024.
当 lim x → x 0 f ( x ) \lim\limits_{x\to x_0}f(x) x→x0limf(x) 存在,当且仅当 lim x → x 0 + f ( x ) = lim x → x 0 − f ( x ) \lim\limits_{x\to {x_0}^+}f(x)=\lim\limits_{x\to {x_0}^-}f(x) x→x0+limf(x)=x→x0−limf(x)( lim x → x 0 − , lim x → x 0 + \lim\limits_{x\to {x_0}^-},\lim\limits_{x\to {x_0}^+} x→x0−lim,x→x0+lim分别为左极限右极限,代表从左或右逼近 x 0 x_0 x0 所得的极限)
若 f ( x ) f(x) f(x) 在 ∣ x ∣ |x| ∣x∣ 大于一正数时有意义,若存在常数 A A A,对于给定 ε > 0 \varepsilon >0 ε>0,总存在 X > 0 X>0 X>0,使得
∀ ∣ x ∣ > X , ∣ f ( x ) − A ∣ < ε \large{\forall} \normalsize |x|>X,|f(x)-A|<\varepsilon ∀∣x∣>X,∣f(x)−A∣<ε
则称 A A A 为 f ( x ) f(x) f(x) 当 x → ∞ x \to \infty x→∞ 的极限,记为 lim x → ∞ f ( x ) = A \lim\limits_{x\to\infty}f(x)=A x→∞limf(x)=A。
函数极限运算
无穷小的和是无穷小。(无穷小指大于 0 0 0 的最小实数)
有界函数与无穷小的乘积为无穷小。
设 lim f ( x ) = A , lim g ( x ) = B \lim f(x) = A,\lim g(x) = B limf(x)=A,limg(x)=B,则
lim
[
f
(
x
)
±
g
(
x
)
]
=
lim
f
(
x
)
±
lim
g
(
x
)
=
A
±
B
\lim[f(x)\pm g(x)]=\lim f(x)\pm\lim g(x)=A\pm B
lim[f(x)±g(x)]=limf(x)±limg(x)=A±B
lim
[
f
(
x
)
g
(
x
)
]
=
lim
f
(
x
)
lim
g
(
x
)
=
A
⋅
B
\lim[f(x)g(x)]=\lim f(x)\lim g(x)=A\cdot B
lim[f(x)g(x)]=limf(x)limg(x)=A⋅B
lim
[
f
(
x
)
g
(
x
)
]
=
lim
f
(
x
)
lim
g
(
x
)
=
A
B
(
g
(
x
)
≠
0
,
B
≠
0
)
\lim[\dfrac{f(x)}{g(x)}]=\dfrac{\lim f(x)}{\lim g(x)}=\dfrac{A}{B}(g(x)\not=0,B\not=0)
lim[g(x)f(x)]=limg(x)limf(x)=BA(g(x)=0,B=0)
若 φ ( x ) ≤ ψ ( x ) \varphi(x)\leq\psi(x) φ(x)≤ψ(x),且 lim φ ( x ) = A , lim ψ ( x ) = B \lim \varphi(x)=A,\lim\psi(x)=B limφ(x)=A,limψ(x)=B,则 A ≤ B A \leq B A≤B
常见函数极限
lim
x
→
x
0
c
=
c
\lim\limits_{x\to x_0}c=c
x→x0limc=c(
c
c
c 为常数)
lim
x
→
x
0
x
a
=
x
0
a
\lim\limits_{x\to x_0}x^a=x_0^a
x→x0limxa=x0a(
a
a
a 为常数,
x
0
x_0
x0 属于幂函数
y
=
x
a
y=x^a
y=xa 的定义域)
lim
x
→
0
sin
x
x
=
1
\lim\limits_{x\to 0}\dfrac{\sin x}{x}=1
x→0limxsinx=1
lim x → x 0 e x − 1 x = 1 \lim\limits_{x\to x_0}\dfrac{e^x-1}{x}=1 x→x0limxex−1=1
函数极限定理
若
lim
x
→
x
0
f
(
x
)
\lim\limits_{x\to x_0}f(x)
x→x0limf(x) 存在,那么这个极限唯一。
若
lim
x
→
x
0
f
(
x
)
=
A
\lim\limits_{x\to x_0}f(x)=A
x→x0limf(x)=A,那么存在常数
M
>
0
M>0
M>0 和
δ
>
0
\delta>0
δ>0,使得当
0
<
∣
x
−
x
0
∣
<
δ
0<|x-x_0|<\delta
0<∣x−x0∣<δ 时,有
∣
f
(
x
)
∣
≤
M
|f(x)|\leq M
∣f(x)∣≤M
若
lim
x
→
x
0
f
(
x
)
\lim\limits_{x\to x_0}f(x)
x→x0limf(x) 存在,
{
x
n
}
\{x_n\}
{xn} 为函数
f
(
x
)
f(x)
f(x) 的定义域内一收敛于
x
0
x_0
x0 的序列,满足
x
n
≠
x
0
(
n
∈
N
+
)
x_n\not=x_0(n\in\mathbb{N}_+)
xn=x0(n∈N+),则相应函数值序列
{
f
(
x
n
)
}
\{f(x_n)\}
{f(xn)} 必收敛,且
lim
n
→
∞
f
(
x
n
)
=
lim
x
→
x
0
f
(
x
)
\lim\limits_{n\to \infty}f(x_n)=\lim\limits_{x\to x_0}f(x)
n→∞limf(xn)=x→x0limf(x)。
导数
导数定义
平均变化率:
x
0
,
x
1
x_0,x_1
x0,x1 为函数
y
=
f
(
x
)
y=f(x)
y=f(x) 定义域内两点,
Δ
x
=
x
0
−
x
1
,
Δ
y
=
f
(
x
0
)
−
f
(
x
1
)
\Delta x = x_0-x_1,\Delta y =f(x_0)-f(x_1)
Δx=x0−x1,Δy=f(x0)−f(x1)。则函数
y
=
f
(
x
)
y=f(x)
y=f(x) 在区间
[
x
0
,
x
1
]
[x_0,x_1]
[x0,x1] 上的平均变化率为:
Δ
y
Δ
x
=
f
(
x
1
+
Δ
x
)
−
f
(
x
1
)
Δ
x
\frac{\Delta y}{\Delta x}=\frac{f(x_1+\Delta x)-f(x_1)}{\Delta x}
ΔxΔy=Δxf(x1+Δx)−f(x1)
瞬时变化率:函数 y = f ( x ) y=f(x) y=f(x) 在 x 0 x_0 x0 附近有定义,当自变量 x = x 0 x = x_0 x=x0 附近改变量为 Δ x \Delta x Δx 时, f ( x 0 ) f(x_0) f(x0) 改变量为 f ( x 0 + Δ x ) − f ( x 0 ) f(x_0+\Delta x)-f(x_0) f(x0+Δx)−f(x0)。如果 δ x \delta x δx 趋近于 0 0 0 时,平均变化率趋近趋近于一个数 l l l,那么 x = x 0 x=x_0 x=x0 处瞬时变化率为 l l l,写作 lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x = l \lim_{\Delta x\to0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} =l limΔx→0Δxf(x0+Δx)−f(x0)=l。
函数在 x 0 x_0 x0 处瞬时变化率通常称为 f ( x ) f(x) f(x) 在 x = x 0 x = x_0 x=x0 处导数,记做 f ′ ( x 0 ) f'(x_0) f′(x0),有:
f ′ ( x 0 ) = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x f'(x_0)=\lim_{\Delta x\to0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} f′(x0)=Δx→0limΔxf(x0+Δx)−f(x0)
导函数:若函数 y = f ( x ) y=f(x) y=f(x) 的导函数为 g ( x ) g(x) g(x),则 ∀ x , g ( x ) = lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x \forall x,g(x)=\lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta x} ∀x,g(x)=limΔx→0Δxf(x+Δx)−f(x)。一般来说, f ( x ) f(x) f(x) 导函数为 f ′ ( x ) f'(x) f′(x)。
连续:对于函数 f ( x ) f(x) f(x),若在 x x x 处 lim x → x 0 + f ( x ) = lim x → x 0 − f ( x ) \lim\limits_{x\to {x_0}^+}f(x)=\lim\limits_{x\to {x_0}^-}f(x) x→x0+limf(x)=x→x0−limf(x),则 f ( x ) f(x) f(x) 在 x x x 处是连续的。
可导:对于函数 f ( x ) f(x) f(x),若在 x x x 处 f + ′ ( x ) = f − ′ ( x ) f'_+(x)=f'_-(x) f+′(x)=f−′(x),则 f ( x ) f(x) f(x) 在 x x x 处是可导的。
常见函数的导数
f
(
x
)
=
c
,
f
′
(
x
)
=
0
f(x)=c,f'(x)=0
f(x)=c,f′(x)=0
f
(
x
)
=
x
a
,
f
′
(
x
)
=
a
x
a
−
1
f(x)=x^a,f'(x)=ax^{a-1}
f(x)=xa,f′(x)=axa−1
f
(
x
)
=
a
x
,
f
′
(
x
)
=
a
x
ln
a
f(x)=a^x,f'(x)=a^x\ln a
f(x)=ax,f′(x)=axlna(
f
(
x
)
=
e
x
,
f
′
(
x
)
=
e
x
f(x)=e^x,f'(x)=e^x
f(x)=ex,f′(x)=ex)
f
(
x
)
=
log
a
x
,
f
′
(
x
)
=
1
x
ln
a
f(x)=\log_ax,f'(x)=\dfrac{1}{x\ln a}
f(x)=logax,f′(x)=xlna1(
f
(
x
)
=
ln
x
,
f
′
(
x
)
=
1
x
f(x)=\ln x,f'(x)=\dfrac{1}{x}
f(x)=lnx,f′(x)=x1)
f
(
x
)
=
sin
x
,
f
′
(
x
)
=
cos
x
f(x)=\sin x,f'(x)=\cos x
f(x)=sinx,f′(x)=cosx
f
(
x
)
=
cos
x
,
f
′
(
x
)
=
−
sin
x
f(x)=\cos x,f'(x)=-\sin x
f(x)=cosx,f′(x)=−sinx
导数的运算
(
f
(
x
)
±
g
(
x
)
)
′
=
f
′
(
x
)
±
g
′
(
x
)
(f(x)\pm g(x))'=f'(x)\pm g'(x)
(f(x)±g(x))′=f′(x)±g′(x)
(
f
(
x
)
g
(
x
)
)
′
=
f
′
(
x
)
g
(
x
)
+
f
(
x
)
g
′
(
x
)
(f(x)g(x))'=f'(x)g(x)+f(x)g'(x)
(f(x)g(x))′=f′(x)g(x)+f(x)g′(x)
(
C
f
(
x
)
)
′
=
C
f
′
(
x
)
(Cf(x))'=Cf'(x)
(Cf(x))′=Cf′(x)
(
f
(
x
)
g
(
x
)
)
′
=
f
′
(
x
)
g
(
x
)
−
f
(
x
)
g
′
(
x
)
g
2
(
x
)
(
g
(
x
)
≠
0
)
(\dfrac{f(x)}{g(x)})'=\dfrac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}(g(x)\not=0)
(g(x)f(x))′=g2(x)f′(x)g(x)−f(x)g′(x)(g(x)=0)
复合函数求导
若对于所有 x x x, f ( g ( x ) ) f(g(x)) f(g(x)) 和 g ( x ) g(x) g(x) 皆可导,则 [ f ( g ( x ) ) ] ′ = f ′ ( g ( x ) ) ⋅ g ′ ( x ) [f(g(x))]'=f'(g(x))\cdot g'(x) [f(g(x))]′=f′(g(x))⋅g′(x)。
导数的几何意义
f ( x ) f(x) f(x) 在 x 0 x_0 x0 处导数的几何意义为其在 ( x 0 , f ( x 0 ) ) (x_0,f(x_0)) (x0,f(x0)) 处切线的斜率。
所以,曲线 f ( x ) f(x) f(x) 在 ( x 0 , f ( x 0 ) ) (x_0,f(x_0)) (x0,f(x0)) 处切线方程可以如下计算:
- 求导,求出 y = f ( x ) y=f(x) y=f(x) 在 x = x 0 x=x_0 x=x0 处导数 f ( x 0 ) f(x_0) f(x0)。
- 已知切点坐标和斜率,求出切线方程。
若 ( x 0 , f ( x 0 ) ) (x_0,f(x_0)) (x0,f(x0)) 处切线平行于 y y y 轴,则方程为 x = x 0 x = x_0 x=x0。
曲线的切线不一定与曲线只有一个交点
在点
P
P
P 的切线和过点
P
P
P 的切线是不同的概念。
二阶导数
定义
一阶导数的导数被称为二阶导数,二阶导数的导数称为三阶导数,以此类推,对一个函数求导 n n n 次的函数称为N阶导数。
一阶导数写作 f ′ ( x ) f'(x) f′(x),二阶写作 f ′ ′ ( x ) f''(x) f′′(x),导数的阶数可以通过 ′ ' ′ 的个数表示, n n n 阶导数也可以写作 f ( n ) ( x ) f^{(n)}(x) f(n)(x)。
在高中仅考察二阶导数,二阶导数的几何意义为切线斜率的变化率。
凹函数与凸函数
凹函数:若
f
(
x
)
f(x)
f(x) 在区间
I
I
I 上连续,且对于
x
1
<
x
2
∈
I
x_1<x_2 \in I
x1<x2∈I,有
f
(
x
1
+
x
2
2
)
<
f
(
x
1
)
+
f
(
x
2
)
2
f(\dfrac{x_1+x_2}{2})<\dfrac{f(x_1)+f(x_2)}{2}
f(2x1+x2)<2f(x1)+f(x2)。若图像为凹函数,则区间
I
I
I 上二阶导数大于
0
0
0。
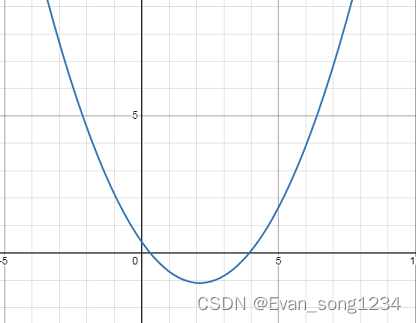
凸函数:若
f
(
x
)
f(x)
f(x) 在区间
I
I
I 上连续,且对于
x
1
<
x
2
∈
I
x_1<x_2 \in I
x1<x2∈I,有
f
(
x
1
+
x
2
2
)
>
f
(
x
1
)
+
f
(
x
2
)
2
f(\dfrac{x_1+x_2}{2})>\dfrac{f(x_1)+f(x_2)}{2}
f(2x1+x2)>2f(x1)+f(x2)。若图像为凸函数,则区间
I
I
I 上二阶导数小于
0
0
0。
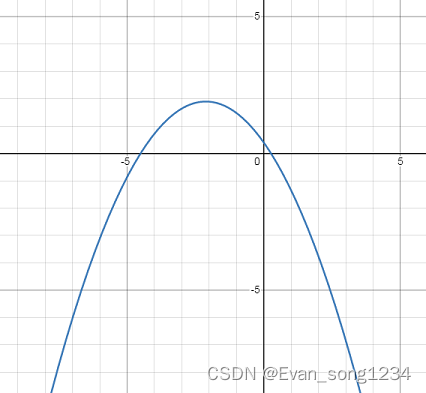
隐函数求导
隐函数定义
方程
F
(
x
,
y
)
=
0
F(x,y) = 0
F(x,y)=0 确定的
x
,
y
x,y
x,y 中,若
y
y
y 是
x
x
x 的函数,则称
y
y
y 为
x
x
x 的隐函数。
有时可以从
F
(
x
,
y
)
=
0
F(x,y)=0
F(x,y)=0 解出
y
=
f
(
x
)
y=f(x)
y=f(x),但有时不可以,如:
y
−
sin
y
+
x
=
0
y-\sin y+x=0
y−siny+x=0。
隐函数求导
若要对 F ( x , y ) F(x,y) F(x,y) 求导,则将 y y y 当做一个函数来求导,例如
2 x sin y + x 3 = 0 2x\sin y+x^3=0 2xsiny+x3=0
求导后则为:
2 sin y + 2 x sin y ⋅ y ′ + 3 x 2 = 0 2\sin y+2x\sin y\cdot y'+3x^2=0 2siny+2xsiny⋅y′+3x2=0
这时,若要计算点 ( x , y ) (x,y) (x,y) 处导数,就直接将 x , y x, y x,y 带入即可求出 y ′ y' y′。
洛必达法则
若 lim x → x 0 f ( x ) g ( x ) \lim\limits_{x\to x_0} \dfrac{f(x)}{g(x)} x→x0limg(x)f(x) 为 0 0 \dfrac{0}{0} 00 或 ∞ ∞ \dfrac{\infty}{\infty} ∞∞ 类型的,则可以用洛必达法则。
洛必达法则:
lim x → x 0 f ( x ) g ( x ) = lim x → x 0 f ′ ( x ) g ′ ( x ) \lim\limits_{x\to x_0} \dfrac{f(x)}{g(x)}=\lim\limits_{x\to x_0}\dfrac{f'(x)}{g'(x)} x→x0limg(x)f(x)=x→x0limg′(x)f′(x)
0 ⋅ ∞ , 1 ∞ , 0 ∞ , ∞ − ∞ 0\cdot\infty,1^\infty,0^\infty,\infty-\infty 0⋅∞,1∞,0∞,∞−∞,等都可以转化成 0 0 \dfrac{0}{0} 00 或 ∞ ∞ \dfrac{\infty}{\infty} ∞∞。
导数应用
函数单调性
若
f
(
x
)
f(x)
f(x) 在一段区间
I
I
I 内,有
f
′
(
x
)
>
0
f'(x)>0
f′(x)>0,则
f
(
x
)
f(x)
f(x) 在
I
I
I 上递增。
若
f
(
x
)
f(x)
f(x) 在一段区间
I
I
I 内,有
f
′
(
x
)
<
0
f'(x)<0
f′(x)<0,则
f
(
x
)
f(x)
f(x) 在
I
I
I 上递减。
函数极值
定义
若在
x
0
x_0
x0 附近都有
f
(
x
)
<
f
(
x
0
)
f(x)<f(x_0)
f(x)<f(x0),则
x
0
x_0
x0 为
f
(
x
)
f(x)
f(x) 的一个极大值点,
f
(
x
0
)
f(x_0)
f(x0) 为
f
(
x
)
f(x)
f(x) 的一个极大值。
若在
x
0
x_0
x0 附近都有
f
(
x
)
>
f
(
x
0
)
f(x)>f(x_0)
f(x)>f(x0),则
x
0
x_0
x0 为
f
(
x
)
f(x)
f(x) 的一个极小值点,
f
(
x
0
)
f(x_0)
f(x0) 为
f
(
x
)
f(x)
f(x) 的一个极小值。
求极值
若
f
(
x
)
f(x)
f(x) 的导数
f
′
(
x
)
f'(x)
f′(x) 在
x
0
x_0
x0 处从正数变成负数,则
f
(
x
)
f(x)
f(x) 在
x
0
x_0
x0 处有极大值。
若
f
(
x
)
f(x)
f(x) 的导数
f
′
(
x
)
f'(x)
f′(x) 在
x
0
x_0
x0 处从负数变成正数,则
f
(
x
)
f(x)
f(x) 在
x
0
x_0
x0 处有极小值。
最值
若要求 f ( x ) f(x) f(x) 在 [ a , b ] [a,b] [a,b] 区间内最值,则先求出 f ( x ) f(x) f(x) 所有极值,然后用 f ( x ) f(x) f(x) 的极值与 f ( a ) , f ( b ) f(a),f(b) f(a),f(b),指比较。取最值即可。






















 521
521











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








