数学之美—细数傅里叶变换原理

最新推荐文章于 2024-01-21 18:32:24 发布

地球被支点撬走啦

最新推荐文章于 2024-01-21 18:32:24 发布

阅读量4.3k

点赞数 3

分类专栏：数学/通信文章标签：数字信号处理

本文链接：https://blog.csdn.net/Flag_ing/article/details/119180196

版权

数学/通信专栏收录该内容

7 篇文章 3 订阅

订阅专栏

一、傅里叶级数（Fourier Series、FS）的实数域表示

二、傅里叶级数（Fourier Series、FS）的复数域表示

三、傅里叶变换（FT）的引出

四、DTFT、DFT、FFT的引出

第一次认识傅里叶（Fourier）是在大二那年的《信号与系统》课上，当时学这门课也不知道有啥用，听的也是一愣一愣的。。最后也仅仅是达到了期末前三天记了点公式，能考个试的水平，当初想着以后怎么也不会再接触通信这鬼东西了，，谁曾想，四年后，在读研之后兜兜转转阴差阳错地又搞起了通信，再回过头来仔细品味四年前学的傅里叶变换豁然开朗，突然觉得数学真是理工科最浪漫的一门学科（之一吧）！

世界上可能有很多巧合，但唯一可以将这些巧合完美地结合在一起并组成一个完美的理论的工具可能只有数学了，这可能就是数学的浪漫与深邃吧~

对周期连续函数进行三角分解，这个过程称作 FS（傅里叶级数）
当周期趋于无穷大，即函数变为非周期连续时，FS 就变成 FT（傅里叶变换）
工程应用中，对非周期连续函数进行时域离散（抽样），变为非周期离散函数，FT 就变为 DTFT（离散时间傅里叶变换）
对非周期离散函数进行时延拓展变为周期离散函数， DTFT 就变为 DFT（离散傅里叶变换）
DFT 的计算复杂度较高，对 DFT 的计算方式进行优化， DFT 就变为 FFT（快速傅里叶变换）

可见傅里叶级数（FS）是FT、DTFT、DFT、FFT的基础，后面变换都是在 FS 的基本原理的基础上衍生出来的，因此，清楚地理解 FS 的基本原理至关重要，因此本文重点讲解 FS 的原理。

一、傅里叶级数（Fourier Series、FS）的实数域表示

学过《高等数学》的小伙伴们一定都知道一个叫做 泰勒级数 的东西：

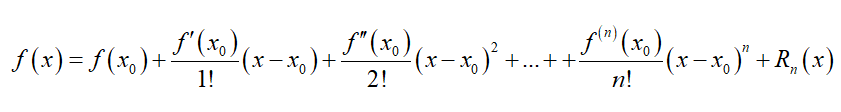
这个东西的原理是使用幂级数的加权组合来表示一个函数在某点 x0 的邻域内的分解。相比傅里叶级数不同的是他只能用来表示函数某个点的邻域内的展开，而且以幂函数为基，但两者都涉及了将信号分解成简单信号的线性组合来表示的思想。

与泰勒级数类似，傅里叶级数是一种对周期信号(即周期函数)的分解表示，它通过对一组成谐波关系的三角函数的加权相加来表示一个周期信号。具体地，如果一个函数是周期函数，那么他就可以被分解成以正弦函数以及余弦函数为基的线性组合。若函数 f(t) 是周期为 T 的周期函数，则其傅里叶级数展开式如下：

公式中， $\omega _{0}$ 称作基波频率， $n\omega _{0}$ 为谐波频率。特别地，a0为直流分量，可以看作 a0=a0cos(0)。

现在傅里叶级数的公式有了，但问题也来了（快记笔记！）：

1、为什么展开式中的函数，不管cos还是sin，都是以 $\omega _{0}$ 为基波的呐？可以是别的值做基波吗？

答：这个好说：必须以 $\omega _{0}$ 作为傅里叶级数的基波。你想呀，只有当傅里叶展开式中的函数都是以基波 $\omega _{0}$ 或者谐波 $n\omega _{0}$ 为角频率时，其每个函数的公共周期才是 T（对于谐波分量，T/n 是其最小周期，但T也是一个周期），这样进行线性组合后的结果的周期才会仍为 T。如果反过来，在众多展开式中加入一个周期为 T1 ≠ T 的分量，显然这样线性组合结果的周期绝对不会是 T 了，也就无法表示 f(t) 了。

2、给定一个周期信号，我怎么选择使用cos还是使用sin还是两者都使用来进行信号的傅里叶级数展开呐？

答：这个也好解释。cos 是偶函数，sin 是奇函数。很明显，当 f(t) 是偶函数的时候，只需要使用 cos 函数进行 FS 展开；当 f(t) 是奇函数的时候，只需要使用 sin 函数进行 FS 展开；当 f(t) 非奇非偶时，因为它必然可以被分解成一个奇函数与一个偶函数的和：

因此，此时需要 cos 和 sin 一起进行 FS 展开。

3、如何计算 FS 的系数 an 及 bn ？

答：这个也不难。通俗点说，an 以及 bn 的值的物理意义就是表征函数 f(x) 与 $\cos \left ( n\omega _{0}t \right )$ 以及 $\sin \left ( n\omega _{0}t \right )$ 的相似程度（或者说相关程度）。换句话说，an 以及 bn 的值表征了 $\cos \left ( n\omega _{0}t \right )$ 以及 $\sin \left ( n\omega _{0}t \right )$ 在线性组合过程中对结果 f(t) 的贡献度。

可以定性地品味一下这句话：如果 f(x) 的图像与 $\cos \left ( n\omega _{0}t \right )$ 或者 $\sin \left ( n\omega _{0}t \right )$ 中的某个函数长得很像，也就意味着其图像的重合部分比较多，那么该 $\cos \left ( n\omega _{0}t \right )$ 或者 $\sin \left ( n\omega _{0}t \right )$ 分量的权值就自然会比较大，这点应该很容易理解，反映到 FS 中就是 an 或者 bn 的值比较大。可以想象一个极端的例子，如果 $f(t)=cos(\omega_{0}t )$ ，那么其傅里叶变换 FS = $cos(\omega_{0}t)$ ，即除了 a1 = 1 之外，其他值都为0，这也是由三角函数的正交性决定的。

那么如何定量计算具体的值呐？这就需要用到相关的概念啦。

对于信号 f1 与信号 f2 的相关的数学定义如下（注意与卷积的区别）：

为了更直观地理解，可以用下图来做说明。图中是两个函数的图像。

对这两个函数做相关运算，结果如下：

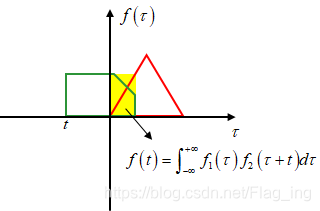
图中两函数绿色区域的值相乘(注意不是相交面积！)即为相关运算的结果，其中，变量 t 可以视为在两函数(原有相位差基础上新增)的相位差，当相位差为0时，相关运算的结果如下：

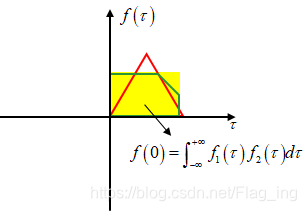
不难理解，对于傅里叶级数来说，原信号 f(t) 与 $\cos \left ( n\omega _{0}t \right )$ 及 $\sin \left ( n\omega _{0}t \right )$ 的相关运算的方式就是图3中的范式。如果只想了解 FS 的原理，看到这里就行了，如果还想得出最后的具体结果那就接着往下看吧。

我们对原信号 f(t) 在一个周期内对 $\cos \left ( n\omega _{0}t \right )$ 求积分，并由三角函数的正交性（傅里叶级数的三角函数项其实就是一个正交函数系）可知：

由此就可以得出:

同理：

特别地，当 n=0 时，sin0=0，cos0=1，此时

这下 an 以及 bn 的值也都解出来了。

上述傅里叶级数的形式含有同频的零相位差的 sin 与 cos 分量，而同频的正弦与余弦分量叠加后频率不变，因此还不能直观地体现出频谱及相位的分布情况。正弦与余弦分量本质是一样的，只是相位差了90°而已。这时，为了将频谱更直观地呈现出来，需要将同频的 cos 与 sin 进行合并：

而可以看出， $n\omega _{0}$ 频率处的幅值及相位由该频率处的正弦份量与余弦分量共同决定，此时 FS 可以改写如下：

这个式子直观的体现了 f(t) 的频谱分量及其所占的比例大小。

至此，傅里叶级数的实数域计算就完成了。

二、傅里叶级数（Fourier Series、FS）的复数域表示

在实际的信号分析问题中，我们遇到的信号表示经常是复数形式的信号（自然界中是不存在复数信号的，但是在运算分析过程中可以使用复信号进行表示以简化计算），但是以上分析只适用于实数域的信号形式。是否有一种 FS 形式可以同时用于实数域与复数域的运算那？答案是肯定的，这下就要先引出一个宇宙最骚公式——欧拉公式：

很多人可能会问：这公式这么写有什么含义呐？其实这个公式在数学应用的角度上只是一个工具，是人为定义的一种形式，公式中 j 的具体意义要在具体的使用环境中做分析，你可以从各种角度来做解析，比如在数学运算中，j 表示的是 -1 的平方根；在信号处理领域中，j就代表复平面中的一个旋转算子。至于这个公式怎么得出来的，答案就是文章开头所说的那样——巧合，恰巧就是这个形式，恰巧用这个规则计算就是对的，恰巧这样计算就是最完美的。。。这就是数学之美吧，不得不佩服欧拉他老人家的想象力。

有了这个公式，就可以使用复数来表示 cos 与 sin 函数了：

将这个结论带入到上面所讲到的 FS 公式中化简，就可以推导出更普适性的傅里叶级数的展开式：

这里的 $c_{n}$ 就是信号 f(t) 对应的频谱。假设f(t)为实函数，下面进行复数域 FS 的反向推导，这种美丽的巧合带来的惊喜即将呈现（^-^）！

首先将 $c_{n}$ 代入，得：

然后为了计算方便，使用以下变量代换：

代换后得：

将变量代换回去得：

现在在回过头去与第一部分讲的 FS 在实数域得展开比较，就问你神奇不哈哈哈

三、傅里叶变换（FT）的引出

傅里叶级数是对周期连续函数进行的分解，但是自然界中的信号几乎都是非周期连续信号，因此我们需要对傅里叶级数进行拓展，先看上面傅里叶级数的复数域的频谱计算公式：

我们可以把非周期函数看作周期无穷大的函数，由于 $\omega _{0}=2\pi /T$ ，随着 T 的增大，频谱间隔 $\omega _{0}$ 无限减小，最终变成连续的频谱，这时的离散频谱就变成了连续频谱，频谱的包络表达式就变成了：

这个表达式就是傅里叶变换(FT)的表达式。

而原来的 FS 的离散频谱系数可以由该连续频谱来获得：

同理，其逆变换此时就成了：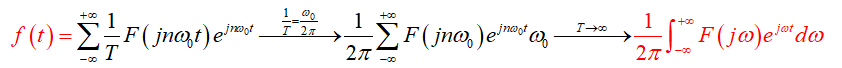

四、DTFT、DFT、FFT的引出

DTFT、DFT、FFT这三种算法是傅里叶变换在工程应用中的延申。在工程应用中，强行手算信号的频谱肯定是不现实的，一般都需要借助计算机来进行辅助计算。FS 及 FT 都是在模拟域计算信号的频谱，但是计算机只能处理数字域的离散信号，因此必须把连续的模拟域信号通过采样转换到离散的数字域才能为计算机所处理，这就需要使用DFT，但是在 DFT 之前还有一个中间过程，就是 DTFT。

DTFT 只对时域进行离散化，其傅里叶变换对公式如下：

可以看出，此时虽然 DTFT 时域是离散的，但其频域（频谱）仍是连续的，而要想计算机顺利计算，频谱必须也是离散的，因此还需要将频域进行离散化，这就是 DFT，DFT 的变换公式如下：

我们将时域离散化为N个点，并进行时延拓展成周期函数，这时进行 N 点的 DFT 计算就会得到 N 点的频谱输出。（这里面涉及一个知识点：时域周期离散对应着频域离散周期，由于这篇文章主要涉及到的工程原理的解释，这个就不展开讨论了）

进一步地，由于直接使用计算机计算 DFT 的时间复杂度太高 [ O(n²) ]，因此需要对 DFT 的计算进行加速，优化后的 DFT 计算方式 [ O(nlogn) ] 就是快速傅里叶算法，即 FFT。

==============================================================

相关连接（以下链接看起来都比较通俗易懂）：

https://www.cnblogs.com/abella/articles/9770989.html

https://www.zhihu.com/question/23234701/answer/26017000

https://www.bilibili.com/video/BV1Tb41187i1

地球被支点撬走啦

关注

3
点赞
踩
29

收藏

觉得还不错? 一键收藏
打赏
0
评论
数学之美—细数傅里叶变换原理

目录一、傅里叶级数（Fourier Series、FS）的实数域表示二、傅里叶级数（Fourier Series、FS）的复数域表示三、傅里叶变换（FT）的引出四、DTFT、DFT、FFT的引出第一次认识傅里叶（Fourier）是在大二那年的《信号与系统》课上，当时学这门课也不知道有啥用，听的也是一愣一愣的。。最后也仅仅是达到了期末前三天记了点公式，能考个试的水平，当初想着以后怎么也不会再接触通信这鬼东西了，，谁曾想，在读研之后兜兜转转阴差阳错地又搞起了通信，再回过头来仔细品味四年前学的
复制链接

扫一扫