OpenCV之imgproc 模块. 图像处理（4）直方图均衡化 直方图计算 直方图对比 反向投影 模板匹配

直方图均衡化

目标

在这个教程中你将学到:

• 什么是图像的直方图和为什么图像的直方图很有用
• 用OpenCV函数 equalizeHist 对图像进行直方图均衡化

原理

图像的直方图是什么?

• 直方图是图像中像素强度分布的图形表达方式.
• 它统计了每一个强度值所具有的像素个数.

直方图均衡化是什么?

• 直方图均衡化是通过拉伸像素强度分布范围来增强图像对比度的一种方法.
• 说得更清楚一些, 以上面的直方图为例, 你可以看到像素主要集中在中间的一些强度值上. 直方图均衡化要做的就是 拉伸 这个范围. 见下面左图: 绿圈圈出了 少有像素分布其上的 强度值. 对其应用均衡化后, 得到了中间图所示的直方图. 均衡化的图像见下面右图.

直方图均衡化是怎样做到的?

• 均衡化指的是把一个分布 (给定的直方图) 映射 到另一个分布 (一个更宽更统一的强度值分布), 所以强度值分布会在整个范围内展开.

• 要想实现均衡化的效果, 映射函数应该是一个 累积分布函数 (cdf) (更多细节, 参考*学习OpenCV*). 对于直方图 , 它的累积分布  是:

  

  要使用其作为映射函数, 我们必须对最大值为255 (或者用图像的最大强度值) 的累积分布  进行归一化. 同上例, 累积分布函数为:

  

• 最后, 我们使用一个简单的映射过程来获得均衡化后像素的强度值:

  

例程

• 咋个例程是用来干嘛的?

  • 加载源图像
  • 把源图像转为灰度图
  • 使用OpenCV函数 EqualizeHist 对直方图均衡化
  • 在窗体中显示源图像和均衡化后图像.

• 下载例程: 点击 这里

• 例程一瞥:

#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include <iostream>
#include <stdio.h>

using namespace cv;
using namespace std;

/**  @function main */
int main( int argc, char** argv )
{
  Mat src, dst;

  char* source_window = "Source image";
  char* equalized_window = "Equalized Image";

  /// 加载源图像
  src = imread( argv[1], 1 );

  if( !src.data )
    { cout<<"Usage: ./Histogram_Demo <path_to_image>"<<endl;
      return -1;}

  /// 转为灰度图
  cvtColor( src, src, CV_BGR2GRAY );

  /// 应用直方图均衡化
  equalizeHist( src, dst );

  /// 显示结果
  namedWindow( source_window, CV_WINDOW_AUTOSIZE );
  namedWindow( equalized_window, CV_WINDOW_AUTOSIZE );

  imshow( source_window, src );
  imshow( equalized_window, dst );

  /// 等待用户按键退出程序
  waitKey(0);

  return 0;
}

说明

1. 声明原图和目标图以及窗体名称:

   Mat src, dst;
   
   char* source_window = "Source image";
   char* equalized_window = "Equalized Image";
   

2. 加载源图像:

   src = imread( argv[1], 1 );
   
   if( !src.data )
     { cout<<"Usage: ./Histogram_Demo <path_to_image>"<<endl;
       return -1;}
   

3. 转为灰度图:

   cvtColor( src, src, CV_BGR2GRAY );
   

4. 利用函数 equalizeHist 对上面灰度图做直方图均衡化:

   equalizeHist( src, dst );
   

   可以看到, 这个操作的参数只有源图像和目标 (均衡化后) 图像.

5. 显示这两个图像 (源图像和均衡化后图像) :

   namedWindow( source_window, CV_WINDOW_AUTOSIZE );
   namedWindow( equalized_window, CV_WINDOW_AUTOSIZE );
   
   imshow( source_window, src );
   imshow( equalized_window, dst );
   

6. 等待用户案件退出程序

   waitKey(0);
   return 0;
   

结果

1. 为了更好地观察直方图均衡化的效果, 我们使用一张对比度不强的图片作为源图像输入, 如下图:

   

   它的直方图为:

   

   注意到像素大多集中在直方图中间的强度上.

2. 使用例程进行均衡化后, 我们得到下面的结果:

   

   这幅图片显然对比度更强. 再验证一下均衡化后图片的直方图:

   

   注意到现在像素在整个强度范围内均衡分布.

Note

 

你们想知道上面的直方图是怎样绘制出来的吗? 请关注接下来的教程!

直方图计算

目标

本文档尝试解答如下问题:

• 如何使用OpenCV函数 split 将图像分割成单通道数组。
• 如何使用OpenCV函数 calcHist 计算图像阵列的直方图。
• 如何使用OpenCV函数 normalize 归一化数组。

Note

 

在上一篇中 (直方图均衡化) 我们介绍了一种特殊直方图叫做 图像直方图 。现在我们从更加广义的角度来考虑直方图的概念，继续往下读!

什么是直方图?

• 直方图是对数据的集合 统计 ，并将统计结果分布于一系列预定义的 bins 中。

• 这里的 数据 不仅仅指的是灰度值 (如上一篇您所看到的)， 统计数据可能是任何能有效描述图像的特征。

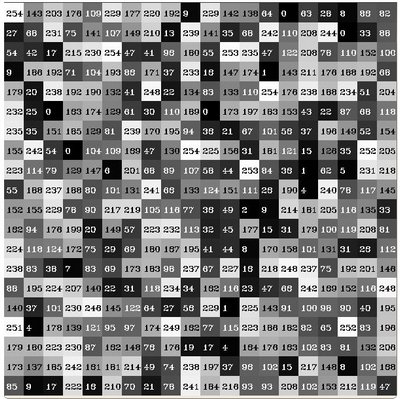
• 先看一个例子吧。 假设有一个矩阵包含一张图像的信息 (灰度值 ):

  

• 如果我们按照某种方式去 统计 这些数字，会发生什么情况呢? 既然已知数字的 范围 包含 256 个值, 我们可以将这个范围分割成子区域(称作 bins)， 如:

  

  然后再统计掉入每一个  的像素数目。采用这一方法来统计上面的数字矩阵，我们可以得到下图( x轴表示 bin， y轴表示各个bin中的像素个数)。

  

• 以上只是一个说明直方图如何工作以及它的用处的简单示例。直方图可以统计的不仅仅是颜色灰度， 它可以统计任何图像特征 (如 梯度, 方向等等)。

• 让我们再来搞清楚直方图的一些具体细节:

  1. dims: 需要统计的特征的数目， 在上例中， dims = 1 因为我们仅仅统计了灰度值(灰度图像)。
  2. bins: 每个特征空间 子区段 的数目，在上例中, bins = 16
  3. range: 每个特征空间的取值范围，在上例中， range = [0,255]

• 怎样去统计两个特征呢? 在这种情况下， 直方图就是3维的了，x轴和y轴分别代表一个特征， z轴是掉入  组合中的样本数目。 同样的方法适用于更高维的情形 (当然会变得很复杂)。

OpenCV的直方图计算

OpenCV提供了一个简单的计算数组集(通常是图像或分割后的通道)的直方图函数 calcHist 。 支持高达 32 维的直方图。下面的代码演示了如何使用该函数计算直方图!

源码

• 本程序做什么?

  • 装载一张图像
  • 使用函数 split 将载入的图像分割成 R, G, B 单通道图像
  • 调用函数 calcHist 计算各单通道图像的直方图
  • 在一个窗口叠加显示3张直方图

• 下载代码: 点击 这里

• 代码一瞥:

#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include <iostream>
#include <stdio.h>

using namespace std;
using namespace cv;

/** @函数 main */
int main( int argc, char** argv )
{
  Mat src, dst;

 /// 装载图像
 src = imread( argv[1], 1 );

 if( !src.data )
   { return -1; }

 /// 分割成3个单通道图像 ( R, G 和 B )
 vector<Mat> rgb_planes;
 split( src, rgb_planes );

 /// 设定bin数目
 int histSize = 255;

 /// 设定取值范围 ( R,G,B) )
 float range[] = { 0, 255 } ;
 const float* histRange = { range };

 bool uniform = true; bool accumulate = false;

 Mat r_hist, g_hist, b_hist;

 /// 计算直方图:
 calcHist( &rgb_planes[0], 1, 0, Mat(), r_hist, 1, &histSize, &histRange, uniform, accumulate );
 calcHist( &rgb_planes[1], 1, 0, Mat(), g_hist, 1, &histSize, &histRange, uniform, accumulate );
 calcHist( &rgb_planes[2], 1, 0, Mat(), b_hist, 1, &histSize, &histRange, uniform, accumulate );

 // 创建直方图画布
 int hist_w = 400; int hist_h = 400;
 int bin_w = cvRound( (double) hist_w/histSize );

 Mat histImage( hist_w, hist_h, CV_8UC3, Scalar( 0,0,0) );

 /// 将直方图归一化到范围 [ 0, histImage.rows ]
 normalize(r_hist, r_hist, 0, histImage.rows, NORM_MINMAX, -1, Mat() );
 normalize(g_hist, g_hist, 0, histImage.rows, NORM_MINMAX, -1, Mat() );
 normalize(b_hist, b_hist, 0, histImage.rows, NORM_MINMAX, -1, Mat() );

 /// 在直方图画布上画出直方图
 for( int i = 1; i < histSize; i++ )
   {
     line( histImage, Point( bin_w*(i-1), hist_h - cvRound(r_hist.at<float>(i-1)) ) ,
                      Point( bin_w*(i), hist_h - cvRound(r_hist.at<float>(i)) ),
                      Scalar( 0, 0, 255), 2, 8, 0  );
     line( histImage, Point( bin_w*(i-1), hist_h - cvRound(g_hist.at<float>(i-1)) ) ,
                      Point( bin_w*(i), hist_h - cvRound(g_hist.at<float>(i)) ),
                      Scalar( 0, 255, 0), 2, 8, 0  );
     line( histImage, Point( bin_w*(i-1), hist_h - cvRound(b_hist.at<float>(i-1)) ) ,
                      Point( bin_w*(i), hist_h - cvRound(b_hist.at<float>(i)) ),
                      Scalar( 255, 0, 0), 2, 8, 0  );
    }

 /// 显示直方图
 namedWindow("calcHist Demo", CV_WINDOW_AUTOSIZE );
 imshow("calcHist Demo", histImage );

 waitKey(0);

 return 0;

}

解释

1. 创建一些矩阵:

   Mat src, dst;
   

2. 装载原图像

   src = imread( argv[1], 1 );
   
   if( !src.data )
     { return -1; }
   

3. 使用OpenCV函数 split 将图像分割成3个单通道图像:

   vector<Mat> rgb_planes;
   split( src, rgb_planes );
   

   输入的是要被分割的图像 (这里包含3个通道)， 输出的则是Mat类型的的向量。

4. 现在对每个通道配置 直方图 设置， 既然我们用到了 R, G 和 B 通道， 我们知道像素值的范围是 

   1. 设定bins数目 (5, 10...):

      int histSize = 255;
      

   2. 设定像素值范围 (前面已经提到,在 0 到 255之间 )

      /// 设定取值范围 ( R,G,B) )
      float range[] = { 0, 255 } ;
      const float* histRange = { range };
      

   3. 我们要把bin范围设定成同样大小(均一)以及开始统计前先清除直方图中的痕迹:

      bool uniform = true; bool accumulate = false;
      

   4. 最后创建储存直方图的矩阵:

      Mat r_hist, g_hist, b_hist;
      

   5. 下面使用OpenCV函数 calcHist 计算直方图:

      /// 计算直方图:
      calcHist( &rgb_planes[0], 1, 0, Mat(), r_hist, 1, &histSize, &histRange, uniform, accumulate );
      calcHist( &rgb_planes[1], 1, 0, Mat(), g_hist, 1, &histSize, &histRange, uniform, accumulate );
      calcHist( &rgb_planes[2], 1, 0, Mat(), b_hist, 1, &histSize, &histRange, uniform, accumulate );
      

      参数说明如下:

      • &rgb_planes[0]: 输入数组(或数组集)
      • 1: 输入数组的个数 (这里我们使用了一个单通道图像，我们也可以输入数组集 )
      • 0: 需要统计的通道 (dim)索引 ，这里我们只是统计了灰度 (且每个数组都是单通道)所以只要写 0 就行了。
      • Mat(): 掩码( 0 表示忽略该像素)， 如果未定义，则不使用掩码
      • r_hist: 储存直方图的矩阵
      • 1: 直方图维数
      • histSize: 每个维度的bin数目
      • histRange: 每个维度的取值范围
      • uniform 和 accumulate: bin大小相同，清楚直方图痕迹

5. 创建显示直方图的画布:

   // 创建直方图画布
   int hist_w = 400; int hist_h = 400;
   int bin_w = cvRound( (double) hist_w/histSize );
   
   Mat histImage( hist_w, hist_h, CV_8UC3, Scalar( 0,0,0) );
   

6. 在画直方图之前，先使用 normalize 归一化直方图，这样直方图bin中的值就被缩放到指定范围:

   /// 将直方图归一化到范围 [ 0, histImage.rows ]
   normalize(r_hist, r_hist, 0, histImage.rows, NORM_MINMAX, -1, Mat() );
   normalize(g_hist, g_hist, 0, histImage.rows, NORM_MINMAX, -1, Mat() );
   normalize(b_hist, b_hist, 0, histImage.rows, NORM_MINMAX, -1, Mat() );
   

   该函数接受下列参数:

   • r_hist: 输入数组
   • r_hist: 归一化后的输出数组(支持原地计算)
   • 0 及 histImage.rows: 这里，它们是归一化 r_hist 之后的取值极限
   • NORM_MINMAX: 归一化方法 (例中指定的方法将数值缩放到以上指定范围)
   • -1: 指示归一化后的输出数组与输入数组同类型
   • Mat(): 可选的掩码

7. 请注意这里如何读取直方图bin中的数据 (此处是一个1维直方图):

     /// 在直方图画布上画出直方图
     for( int i = 1; i < histSize; i++ )
       {
         line( histImage, Point( bin_w*(i-1), hist_h - cvRound(r_hist.at<float>(i-1)) ) ,
                             Point( bin_w*(i), hist_h - cvRound(r_hist.at<float>(i)) ),
                             Scalar( 0, 0, 255), 2, 8, 0  );
   
         line( histImage, Point( bin_w*(i-1), hist_h - cvRound(g_hist.at<float>(i-1)) ) ,
                             Point( bin_w*(i), hist_h - cvRound(g_hist.at<float>(i)) ),
                             Scalar( 0, 255, 0), 2, 8, 0  );
   
         line( histImage, Point( bin_w*(i-1), hist_h - cvRound(b_hist.at<float>(i-1)) ) ,
                             Point( bin_w*(i), hist_h - cvRound(b_hist.at<float>(i)) ),
                             Scalar( 255, 0, 0), 2, 8, 0  );
       }
   
   
   使用了以下表达式:
   
   .. code-block:: cpp
   
      r_hist.at<float>(i)
   
   
     :math:`i` 指示维度，假如我们要访问2维直方图，我们就要用到这样的表达式:
   
   .. code-block:: cpp
   
      r_hist.at<float>( i, j )

8. 最后显示直方图并等待用户退出程序:

   namedWindow("calcHist Demo", CV_WINDOW_AUTOSIZE );
   imshow("calcHist Demo", histImage );
   
   waitKey(0);
   
   return 0;
   

结果

1. 使用下图作为输入图像:

   

2. 产生以下直方图:

   

直方图对比

目标

本文档尝试解答如下问题:

• 如何使用OpenCV函数 compareHist 产生一个表达两个直方图的相似度的数值。
• 如何使用不同的对比标准来对直方图进行比较。

原理

• 要比较两个直方图(  and  ), 首先必须要选择一个衡量直方图相似度的 对比标准 () 。

• OpenCV 函数 compareHist 执行了具体的直方图对比的任务。该函数提供了4种对比标准来计算相似度：

  1. Correlation ( CV_COMP_CORREL )

     

     其中

     

      是直方图中bin的数目。

  2. Chi-Square ( CV_COMP_CHISQR )

     

  3. Intersection ( CV_COMP_INTERSECT )

     

  4. Bhattacharyya 距离( CV_COMP_BHATTACHARYYA )

     

源码

• 本程序做什么?

  • 装载一张 基准图像 和 两张 测试图像 进行对比。
  • 产生一张取自 基准图像 下半部的图像。
  • 将图像转换到HSV格式。
  • 计算所有图像的H-S直方图，并归一化以便对比。
  • 将 基准图像 直方图与 两张测试图像直方图，基准图像半身像直方图，以及基准图像本身的直方图分别作对比。
  • 显示计算所得的直方图相似度数值。

• 下载代码: 点击 这里

• 代码一瞥:

#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include <iostream>
#include <stdio.h>

using namespace std;
using namespace cv;

/** @函数 main */
int main( int argc, char** argv )
{
  Mat src_base, hsv_base;
  Mat src_test1, hsv_test1;
  Mat src_test2, hsv_test2;
  Mat hsv_half_down;

  /// 装载三张背景环境不同的图像
  if( argc < 4 )
    { printf("** Error. Usage: ./compareHist_Demo <image_settings0> <image_setting1> <image_settings2>\n");
      return -1;
    }

  src_base = imread( argv[1], 1 );
  src_test1 = imread( argv[2], 1 );
  src_test2 = imread( argv[3], 1 );

  /// 转换到 HSV
  cvtColor( src_base, hsv_base, CV_BGR2HSV );
  cvtColor( src_test1, hsv_test1, CV_BGR2HSV );
  cvtColor( src_test2, hsv_test2, CV_BGR2HSV );

  hsv_half_down = hsv_base( Range( hsv_base.rows/2, hsv_base.rows - 1 ), Range( 0, hsv_base.cols - 1 ) );

  /// 对hue通道使用30个bin,对saturatoin通道使用32个bin
  int h_bins = 50; int s_bins = 60;
  int histSize[] = { h_bins, s_bins };

  // hue的取值范围从0到256, saturation取值范围从0到180
  float h_ranges[] = { 0, 256 };
  float s_ranges[] = { 0, 180 };

  const float* ranges[] = { h_ranges, s_ranges };

  // 使用第0和第1通道
  int channels[] = { 0, 1 };

  /// 直方图
  MatND hist_base;
  MatND hist_half_down;
  MatND hist_test1;
  MatND hist_test2;

  /// 计算HSV图像的直方图
  calcHist( &hsv_base, 1, channels, Mat(), hist_base, 2, histSize, ranges, true, false );
  normalize( hist_base, hist_base, 0, 1, NORM_MINMAX, -1, Mat() );

  calcHist( &hsv_half_down, 1, channels, Mat(), hist_half_down, 2, histSize, ranges, true, false );
  normalize( hist_half_down, hist_half_down, 0, 1, NORM_MINMAX, -1, Mat() );

  calcHist( &hsv_test1, 1, channels, Mat(), hist_test1, 2, histSize, ranges, true, false );
  normalize( hist_test1, hist_test1, 0, 1, NORM_MINMAX, -1, Mat() );

  calcHist( &hsv_test2, 1, channels, Mat(), hist_test2, 2, histSize, ranges, true, false );
  normalize( hist_test2, hist_test2, 0, 1, NORM_MINMAX, -1, Mat() );

  ///应用不同的直方图对比方法
  for( int i = 0; i < 4; i++ )
     { int compare_method = i;
       double base_base = compareHist( hist_base, hist_base, compare_method );
       double base_half = compareHist( hist_base, hist_half_down, compare_method );
       double base_test1 = compareHist( hist_base, hist_test1, compare_method );
       double base_test2 = compareHist( hist_base, hist_test2, compare_method );

       printf( " Method [%d] Perfect, Base-Half, Base-Test(1), Base-Test(2) : %f, %f, %f, %f \n", i, base_base, base_half , base_test1, base_test2 );
     }

  printf( "Done \n" );

  return 0;
 }

解释

1. 声明储存基准图像和另外两张对比图像的矩阵( RGB 和 HSV )

   Mat src_base, hsv_base;
   Mat src_test1, hsv_test1;
   Mat src_test2, hsv_test2;
   Mat hsv_half_down;
   

2. 装载基准图像(src_base) 和两张测试图像:

   if( argc < 4 )
     { printf("** Error. Usage: ./compareHist_Demo <image_settings0> <image_setting1> <image_settings2>\n");
       return -1;
     }
   
   src_base = imread( argv[1], 1 );
   src_test1 = imread( argv[2], 1 );
   src_test2 = imread( argv[3], 1 );
   

3. 将图像转化到HSV格式:

   cvtColor( src_base, hsv_base, CV_BGR2HSV );
   cvtColor( src_test1, hsv_test1, CV_BGR2HSV );
   cvtColor( src_test2, hsv_test2, CV_BGR2HSV );
   

4. 同时创建包含基准图像下半部的半身图像(HSV格式):

   hsv_half_down = hsv_base( Range( hsv_base.rows/2, hsv_base.rows - 1 ), Range( 0, hsv_base.cols - 1 ) );
   

5. 初始化计算直方图需要的实参(bins, 范围，通道 H 和 S ).

   int h_bins = 50; int s_bins = 32;
   int histSize[] = { h_bins, s_bins };
   
   float h_ranges[] = { 0, 256 };
   float s_ranges[] = { 0, 180 };
   
   const float* ranges[] = { h_ranges, s_ranges };
   
   int channels[] = { 0, 1 };
   

6. 创建储存直方图的 MatND 实例:

   MatND hist_base;
   MatND hist_half_down;
   MatND hist_test1;
   MatND hist_test2;
   

7. 计算基准图像，两张测试图像，半身基准图像的直方图:

   calcHist( &hsv_base, 1, channels, Mat(), hist_base, 2, histSize, ranges, true, false );
   normalize( hist_base, hist_base, 0, 1, NORM_MINMAX, -1, Mat() );
   
   calcHist( &hsv_half_down, 1, channels, Mat(), hist_half_down, 2, histSize, ranges, true, false );
   normalize( hist_half_down, hist_half_down, 0, 1, NORM_MINMAX, -1, Mat() );
   
   calcHist( &hsv_test1, 1, channels, Mat(), hist_test1, 2, histSize, ranges, true, false );
   normalize( hist_test1, hist_test1, 0, 1, NORM_MINMAX, -1, Mat() );
   
   calcHist( &hsv_test2, 1, channels, Mat(), hist_test2, 2, histSize, ranges, true, false );
   normalize( hist_test2, hist_test2, 0, 1, NORM_MINMAX, -1, Mat() );
   

8. 按顺序使用4种对比标准将基准图像(hist_base)的直方图与其余各直方图进行对比:

   for( int i = 0; i < 4; i++ )
      { int compare_method = i;
        double base_base = compareHist( hist_base, hist_base, compare_method );
        double base_half = compareHist( hist_base, hist_half_down, compare_method );
        double base_test1 = compareHist( hist_base, hist_test1, compare_method );
        double base_test2 = compareHist( hist_base, hist_test2, compare_method );
   
       printf( " Method [%d] Perfect, Base-Half, Base-Test(1), Base-Test(2) : %f, %f, %f, %f \n", i, base_base, base_half , base_test1, base_test2 );
     }
   

结果

1. 使用下列输入图像:

   第一张为基准图像，其余两张为测试图像。同时我们会将基准图像与它自身及其半身图像进行对比。

2. 我们应该会预料到当将基准图像直方图及其自身进行对比时会产生完美的匹配， 当与来源于同一样的背景环境的半身图对比时应该会有比较高的相似度， 当与来自不同亮度光照条件的其余两张测试图像对比时匹配度应该不是很好:

3. 下面显示的是结果数值:

对比标准	基准 - 基准	基准 - 半身	基准 - 测试1	基准 - 测试2
Correlation	1.000000	0.930766	0.182073	0.120447
Chi-square	0.000000	4.940466	21.184536	49.273437
Intersection	24.391548	14.959809	3.889029	5.775088
Bhattacharyya	0.000000	0.222609	0.646576	0.801869

对于 Correlation 和 Intersection 标准, 值越大相似度越大。因此可以看到对于采用这两个方法的对比，*基准 - 基准* 的对比结果值是最大的， 而 基准 - 半身 的匹配则是第二好(跟我们预测的一致)。而另外两种对比标准，则是结果越小相似度越大。 我们可以观察到基准图像直方图与两张测试图像直方图的匹配是最差的，这再一次印证了我们的预测。

反向投影

目标

本文档尝试解答如下问题:

• 什么是反向投影，它可以实现什么功能？
• 如何使用OpenCV函数 calcBackProject 计算反向投影？
• 如何使用OpenCV函数 mixChannels 组合图像的不同通道？

原理

什么是反向投影？

• 反向投影是一种记录给定图像中的像素点如何适应直方图模型像素分布的方式。
• 简单的讲， 所谓反向投影就是首先计算某一特征的直方图模型，然后使用模型去寻找图像中存在的该特征。
• 例如， 你有一个肤色直方图 ( Hue-Saturation 直方图 ),你可以用它来寻找图像中的肤色区域:

反向投影的工作原理?

• 我们使用肤色直方图为例来解释反向投影的工作原理:

• 假设你已经通过下图得到一个肤色直方图(Hue-Saturation)， 旁边的直方图就是 模型直方图 ( 代表手掌的皮肤色调).你可以通过掩码操作来抓取手掌所在区域的直方图:

• 下图是另一张手掌图(测试图像) 以及对应的整张图像的直方图:

• 我们要做的就是使用 模型直方图 (代表手掌的皮肤色调) 来检测测试图像中的皮肤区域。以下是检测的步骤

  1. 对测试图像中的每个像素 (  ),获取色调数据并找到该色调(  )在直方图中的bin的位置。

  2. 查询 模型直方图 中对应的bin -  - 并读取该bin的数值。

  3. 将此数值储存在新的图像中(BackProjection)。 你也可以先归一化 模型直方图 ,这样测试图像的输出就可以在屏幕显示了。

  4. 通过对测试图像中的每个像素采用以上步骤， 我们得到了下面的 BackProjection 结果图:

     

  5. 使用统计学的语言, BackProjection 中储存的数值代表了测试图像中该像素属于皮肤区域的 概率 。比如以上图为例， 亮起的区域是皮肤区域的概率更大(事实确实如此),而更暗的区域则表示更低的概率(注意手掌内部和边缘的阴影影响了检测的精度)。

源码

• 本程序做什么?

  • 装载图像

  • 转换原图像到 HSV 格式，再分离出 Hue 通道来建立直方图 (使用 OpenCV 函数 mixChannels)

  • 让用户输入建立直方图所需的bin的数目。

    • 计算同一图像的直方图 (如果bin的数目改变则更新直方图) 和反向投影图。

  • 显示反向投影图和直方图。

• 下载源码:

  1. 点击 这里 获取简单版的源码 (本教程使用简单版)。
  2. 要尝试更炫的代码 (使用 H-S 直方图和 floodFill 来定义皮肤区域的掩码)你可以点击 增强版演示
  3. 当然你也可以从实例库里下载经典的 camshiftdemo 示例。

• 代码一瞥:

#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"

#include <iostream>

using namespace cv;
using namespace std;

/// 全局变量
Mat src; Mat hsv; Mat hue;
int bins = 25;

/// 函数申明
void Hist_and_Backproj(int, void* );

/** @函数 main */
int main( int argc, char** argv )
{
  /// 读取图像
  src = imread( argv[1], 1 );
  /// 转换到 HSV 空间
  cvtColor( src, hsv, CV_BGR2HSV );

  /// 分离 Hue 通道
  hue.create( hsv.size(), hsv.depth() );
  int ch[] = { 0, 0 };
  mixChannels( &hsv, 1, &hue, 1, ch, 1 );

  /// 创建 Trackbar 来输入bin的数目
  char* window_image = "Source image";
  namedWindow( window_image, CV_WINDOW_AUTOSIZE );
  createTrackbar("* Hue  bins: ", window_image, &bins, 180, Hist_and_Backproj );
  Hist_and_Backproj(0, 0);

  /// 现实图像
  imshow( window_image, src );

  /// 等待用户反应
  waitKey(0);
  return 0;
}


/**
 * @函数 Hist_and_Backproj
 * @简介：Trackbar事件的回调函数
 */
void Hist_and_Backproj(int, void* )
{
  MatND hist;
  int histSize = MAX( bins, 2 );
  float hue_range[] = { 0, 180 };
  const float* ranges = { hue_range };

  /// 计算直方图并归一化
  calcHist( &hue, 1, 0, Mat(), hist, 1, &histSize, &ranges, true, false );
  normalize( hist, hist, 0, 255, NORM_MINMAX, -1, Mat() );

  /// 计算反向投影
  MatND backproj;
  calcBackProject( &hue, 1, 0, hist, backproj, &ranges, 1, true );

  /// 显示反向投影
  imshow( "BackProj", backproj );

  /// 显示直方图
  int w = 400; int h = 400;
  int bin_w = cvRound( (double) w / histSize );
  Mat histImg = Mat::zeros( w, h, CV_8UC3 );

  for( int i = 0; i < bins; i ++ )
     { rectangle( histImg, Point( i*bin_w, h ), Point( (i+1)*bin_w, h - cvRound( hist.at<float>(i)*h/255.0 ) ), Scalar( 0, 0, 255 ), -1 ); }

  imshow( "Histogram", histImg );
}

解释

1. 申明图像矩阵，初始化bin数目:

   Mat src; Mat hsv; Mat hue;
   int bins = 25;
   

2. 读取输入图像并转换到HSV 格式:

   src = imread( argv[1], 1 );
   cvtColor( src, hsv, CV_BGR2HSV );
   

3. 本教程仅仅使用Hue通道来创建1维直方图 (你可以从上面的链接下载增强版本,增强版本使用了更常见的H-S直方图，以获取更好的结果):

   hue.create( hsv.size(), hsv.depth() );
   int ch[] = { 0, 0 };
   mixChannels( &hsv, 1, &hue, 1, ch, 1 );
   

   你可以看到这里我们使用 mixChannels 来抽取 HSV图像的0通道(Hue)。 该函数接受了以下的实参:

   • &hsv: 一系列输入图像的数组， 被拷贝的通道的来源
   • 1: 输入数组中图像的数目
   • &hue: 一系列目的图像的数组， 储存拷贝的通道
   • 1: 目的数组中图像的数目
   • ch[] = {0,0}: 通道索引对的数组，指示如何将输入图像的某一通道拷贝到目的图像的某一通道。在这里，&hsv图像的Hue(0) 通道被拷贝到&hue图像(单通道)的0 通道。
   • 1: 通道索引对德数目

4. 创建Trackbar方便用户输入bin数目。 Trackbar的任何变动将会调用函数 Hist_and_Backproj 。

   char* window_image = "Source image";
   namedWindow( window_image, CV_WINDOW_AUTOSIZE );
   createTrackbar("* Hue  bins: ", window_image, &bins, 180, Hist_and_Backproj );
   Hist_and_Backproj(0, 0);
   

5. 显示并等待用户突出程序:

   imshow( window_image, src );
   
   waitKey(0);
   return 0;
   

6. Hist_and_Backproj 函数: 初始化函数 calcHist 需要的实参， bin数目来自于 Trackbar:

   void Hist_and_Backproj(int, void* )
   {
     MatND hist;
     int histSize = MAX( bins, 2 );
     float hue_range[] = { 0, 180 };
     const float* ranges = { hue_range };
   

7. 计算直方图并归一化到范围 

   calcHist( &hue, 1, 0, Mat(), hist, 1, &histSize, &ranges, true, false );
   normalize( hist, hist, 0, 255, NORM_MINMAX, -1, Mat() );
   

8. 调用函数 calcBackProject 计算同一张图像的反向投影

   MatND backproj;
   calcBackProject( &hue, 1, 0, hist, backproj, &ranges, 1, true );
   

   所有的实参都已经知道了(与计算直方图的实参一样), 仅仅增加了 backproj 矩阵,用来储存原图像(&hue)的反向投影。

9. 显示 backproj:

   imshow( "BackProj", backproj );
   

10. 显示1维 Hue 直方图:

    int w = 400; int h = 400;
    int bin_w = cvRound( (double) w / histSize );
    Mat histImg = Mat::zeros( w, h, CV_8UC3 );
    
    for( int i = 0; i < bins; i ++ )
       { rectangle( histImg, Point( i*bin_w, h ), Point( (i+1)*bin_w, h - cvRound( hist.at<float>(i)*h/255.0 ) ), Scalar( 0, 0, 255 ), -1 ); }
    
    imshow( "Histogram", histImg );
    

结果

1. 下面是对一张样本图像(猜猜是什么?又是一掌)进行的测试结果。 你可以改变bin的数目来观察它是如何影响结果图像的:

模板匹配

目标

在这节教程中您将学到:

• 使用OpenCV函数 matchTemplate 在模板块和输入图像之间寻找匹配,获得匹配结果图像
• 使用OpenCV函数 minMaxLoc 在给定的矩阵中寻找最大和最小值(包括它们的位置).

原理

什么是模板匹配?

模板匹配是一项在一幅图像中寻找与另一幅模板图像最匹配(相似)部分的技术.

它是怎么实现的?

• 我们需要2幅图像:

  1. 原图像 (I): 在这幅图像里,我们希望找到一块和模板匹配的区域
  2. 模板 (T): 将和原图像比照的图像块

  我们的目标是检测最匹配的区域:

  

• 为了确定匹配区域, 我们不得不滑动模板图像和原图像进行 比较 :

  

• 通过 滑动, 我们的意思是图像块一次移动一个像素 (从左往右,从上往下). 在每一个位置, 都进行一次度量计算来表明它是 “好” 或 “坏” 地与那个位置匹配 (或者说块图像和原图像的特定区域有多么相似).

• 对于 T 覆盖在 I 上的每个位置,你把度量值 保存 到 结果图像矩阵 (R) 中. 在 R 中的每个位置  都包含匹配度量值:

  

  上图就是 TM_CCORR_NORMED 方法处理后的结果图像 R . 最白的位置代表最高的匹配. 正如您所见, 红色椭圆框住的位置很可能是结果图像矩阵中的最大数值, 所以这个区域 (以这个点为顶点,长宽和模板图像一样大小的矩阵) 被认为是匹配的.

• 实际上, 我们使用函数 minMaxLoc 来定位在矩阵 R 中的最大值点 (或者最小值, 根据函数输入的匹配参数) .

OpenCV中支持哪些匹配算法?

问得好. OpenCV通过函数 matchTemplate 实现了模板匹配算法. 可用的方法有6个:

1. 平方差匹配 method=CV_TM_SQDIFF

这类方法利用平方差来进行匹配,最好匹配为0.匹配越差,匹配值越大.

2. 标准平方差匹配 method=CV_TM_SQDIFF_NORMED

   

3. 相关匹配 method=CV_TM_CCORR

这类方法采用模板和图像间的乘法操作,所以较大的数表示匹配程度较高,0标识最坏的匹配效果.

4. 标准相关匹配 method=CV_TM_CCORR_NORMED

   

5. 相关匹配 method=CV_TM_CCOEFF

这类方法将模版对其均值的相对值与图像对其均值的相关值进行匹配,1表示完美匹配,-1表示糟糕的匹配,0表示没有任何相关性(随机序列).

在这里

6. 标准相关匹配 method=CV_TM_CCOEFF_NORMED

   

通常,随着从简单的测量(平方差)到更复杂的测量(相关系数),我们可获得越来越准确的匹配(同时也意味着越来越大的计算代价). 最好的办法是对所有这些设置多做一些测试实验,以便为自己的应用选择同时兼顾速度和精度的最佳方案.

代码

• 在这程序实现了什么?

  • 载入一幅输入图像和一幅模板图像块 (template)
  • 通过使用函数 matchTemplate 实现之前所述的6种匹配方法的任一个. 用户可以通过滑动条选取任何一种方法.
  • 归一化匹配后的输出结果
  • 定位最匹配的区域
  • 用矩形标注最匹配的区域

• 下载代码: 单击 这里

• 看一下代码:

#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include <iostream>
#include <stdio.h>

using namespace std;
using namespace cv;

/// 全局变量
Mat img; Mat templ; Mat result;
char* image_window = "Source Image";
char* result_window = "Result window";

int match_method;
int max_Trackbar = 5;

/// 函数声明
void MatchingMethod( int, void* );

/** @主函数 */
int main( int argc, char** argv )
{
  /// 载入原图像和模板块
  img = imread( argv[1], 1 );
  templ = imread( argv[2], 1 );

  /// 创建窗口
  namedWindow( image_window, CV_WINDOW_AUTOSIZE );
  namedWindow( result_window, CV_WINDOW_AUTOSIZE );

  /// 创建滑动条
  char* trackbar_label = "Method: \n 0: SQDIFF \n 1: SQDIFF NORMED \n 2: TM CCORR \n 3: TM CCORR NORMED \n 4: TM COEFF \n 5: TM COEFF NORMED";
  createTrackbar( trackbar_label, image_window, &match_method, max_Trackbar, MatchingMethod );

  MatchingMethod( 0, 0 );

  waitKey(0);
  return 0;
}

/**
 * @函数 MatchingMethod
 * @简单的滑动条回调函数
 */
void MatchingMethod( int, void* )
{
  /// 将被显示的原图像
  Mat img_display;
  img.copyTo( img_display );

  /// 创建输出结果的矩阵
  int result_cols =  img.cols - templ.cols + 1;
  int result_rows = img.rows - templ.rows + 1;

  result.create( result_cols, result_rows, CV_32FC1 );

  /// 进行匹配和标准化
  matchTemplate( img, templ, result, match_method );
  normalize( result, result, 0, 1, NORM_MINMAX, -1, Mat() );

  /// 通过函数 minMaxLoc 定位最匹配的位置
  double minVal; double maxVal; Point minLoc; Point maxLoc;
  Point matchLoc;

  minMaxLoc( result, &minVal, &maxVal, &minLoc, &maxLoc, Mat() );

  /// 对于方法 SQDIFF 和 SQDIFF_NORMED, 越小的数值代表更高的匹配结果. 而对于其他方法, 数值越大匹配越好
  if( match_method  == CV_TM_SQDIFF || match_method == CV_TM_SQDIFF_NORMED )
    { matchLoc = minLoc; }
  else
    { matchLoc = maxLoc; }

  /// 让我看看您的最终结果
  rectangle( img_display, matchLoc, Point( matchLoc.x + templ.cols , matchLoc.y + templ.rows ), Scalar::all(0), 2, 8, 0 );
  rectangle( result, matchLoc, Point( matchLoc.x + templ.cols , matchLoc.y + templ.rows ), Scalar::all(0), 2, 8, 0 );

  imshow( image_window, img_display );
  imshow( result_window, result );

  return;
}

代码说明

1. 定义一些全局变量, 例如原图像(img), 模板图像(templ) 和结果图像(result) , 还有匹配方法以及窗口名称:

   Mat img; Mat templ; Mat result;
   char* image_window = "Source Image";
   char* result_window = "Result window";
   
   int match_method;
   int max_Trackbar = 5;
   

2. 载入原图像和匹配块:

   img = imread( argv[1], 1 );
   templ = imread( argv[2], 1 );
   

3. 创建窗口,显示原图像和结果图像:

   namedWindow( image_window, CV_WINDOW_AUTOSIZE );
   namedWindow( result_window, CV_WINDOW_AUTOSIZE );
   

4. 创建滑动条并输入将被使用的匹配方法. 一旦滑动条发生改变,回调函数 MatchingMethod 就会被调用.

   char* trackbar_label = "Method: \n 0: SQDIFF \n 1: SQDIFF NORMED \n 2: TM CCORR \n 3: TM CCORR NORMED \n 4: TM COEFF \n 5: TM COEFF NORMED";
   createTrackbar( trackbar_label, image_window, &match_method, max_Trackbar, MatchingMethod );
   

5. 一直等待,直到用户退出这个程序.

   waitKey(0);
   return 0;
   

6. 让我们先看看回调函数. 首先, 它对原图像进行了一份复制:

   Mat img_display;
   img.copyTo( img_display );
   

7. 然后, 它创建了一幅用来存放匹配结果的输出图像矩阵. 仔细看看输出矩阵的大小(它包含了所有可能的匹配位置)

   int result_cols =  img.cols - templ.cols + 1;
   int result_rows = img.rows - templ.rows + 1;
   
   result.create( result_cols, result_rows, CV_32FC1 );
   

8. 执行模板匹配操作:

   matchTemplate( img, templ, result, match_method );
   

   很自然地,参数是输入图像 I, 模板图像 T, 结果图像 R 还有匹配方法 (通过滑动条给出)

9. 我们对结果进行归一化:

   normalize( result, result, 0, 1, NORM_MINMAX, -1, Mat() );
   

10. 通过使用函数 minMaxLoc ,我们确定结果矩阵 R 的最大值和最小值的位置.

    double minVal; double maxVal; Point minLoc; Point maxLoc;
    Point matchLoc;
    
    minMaxLoc( result, &minVal, &maxVal, &minLoc, &maxLoc, Mat() );
    

    函数中的参数有:

    • result: 匹配结果矩阵
    • &minVal 和 &maxVal: 在矩阵 result 中存储的最小值和最大值
    • &minLoc 和 &maxLoc: 在结果矩阵中最小值和最大值的坐标.
    • Mat(): 可选的掩模

11. 对于前二种方法 ( CV_SQDIFF 和 CV_SQDIFF_NORMED ) 最低的数值标识最好的匹配. 对于其他的, 越大的数值代表越好的匹配. 所以, 我们在 matchLoc 中存放相符的变量值:

    if( match_method  == CV_TM_SQDIFF || match_method == CV_TM_SQDIFF_NORMED )
      { matchLoc = minLoc; }
    else
      { matchLoc = maxLoc; }
    

12. 显示原图像和结果图像. 再用矩形框标注最符合的区域:

    rectangle( img_display, matchLoc, Point( matchLoc.x + templ.cols , matchLoc.y + templ.rows ), Scalar::all(0), 2, 8, 0 );
    rectangle( result, matchLoc, Point( matchLoc.x + templ.cols , matchLoc.y + templ.rows ), Scalar::all(0), 2, 8, 0 );
    
    imshow( image_window, img_display );
    imshow( result_window, result );
    

结果

1. 开始测试我们的程序,一幅输入图像:

   

   还有一幅模版图像:

   

2. 产生了一下结果图像矩阵 (第一行是标准的方法 SQDIFF, CCORR 和 CCOEFF, 第二行是相同的方法在进行标准化后的图像). 在第1列, 最黑的部分代表最好的匹配, 对于其它2列, 越白的区域代表越好的匹配.

3. 正确的匹配在下面显示 (右侧被矩形标注的人脸). 需要注意的是方法 CCORR 和 CCOEFF 给出了错误的匹配结果, 但是它们的归一化版本给出了正确的结果, 这或许是由于我们实际上仅仅考虑 “最匹配” 而没考虑其他可能的高匹配位置.

   

from: http://www.opencv.org.cn/opencvdoc/2.3.2/html/doc/tutorials/imgproc/table_of_content_imgproc/table_of_content_imgproc.html#table-of-content-imgproc