深度学习笔记

写在前面：将2021暑假所学的内容用博客记录下，当中的内容很多以前学过，暑假再次巩固并重新推导了相关公式，由于自己手写的太丑太乱，大部分沿用了参考文章的公式以及符号标记方式。

#第一部分 机器学习

一、监督学习和无监督学习

1.监督学习

通过网上的学习课程，以下是我对监督学习的理解：

从实现目标来看，监督学习算法最终实现的是一种模型的构建，该模型针对输入数据，最终得到一个目标输出。对于模型的构建，首先初始化模型，根据训练数据集不断修正模型，并在最终得到最优目标模型。注意，这里的训练数据集包括输入数据和对应的输出结果，也即数据集都是有标签的、有意义的。

从而得到监督学习的模型框架如下所示：

1.1 线性回归

1.1.1方法步骤

​ 线性回归问题是预测问题，它经过监督学习之后拟合得到一个函数$f$​,该函数针对输入$x$​得到输出$y$​,也即$y=f(x)$​​。

​ 针对线性回归，该模型有以下步骤完成：

• 确定目标函数

  该函数也即模型要拟合预测的函数，这里以$f(x)={\theta }_0+{\theta }_1\ast x$​​为例。

• 确定损失函数

  该函数用以衡量，在给定数据集下，当前模型输出结果与预期给定的输出结果的差距大小。可以用交叉熵、误差平方等来衡量。这里以误差平方和为例：

  $J({\theta }_0,{\theta }_1,...,{\theta }_n)=\frac{1}{2m}{\sum }_{i=1}^m{(f(x^{(i)})-y^{(i)})}^2$

  显然，我们希望$J(\theta )$的值越小越好，这样模型的预测值与原预期值的差距就越小，最终的预测结果越准确。

• 梯度下降，更新权重

  我认为梯度下降是机器学习的灵魂，它是机器学习模型训练数据后向预期方向更新数据的方法。

  根据梯度下降的原理，设置学习步长$\alpha$，根据下式更新各个权重：

  ${\theta }_j={\theta }_j-\alpha \frac{1}{m}{\sum }_{i=0}^m(f(x^{(i)})-y^{(i)})x_j^{(i)}$​

  注意，这里的$m$​​为训练样本数量

• 确定训练数据集、训练次数、训练轮次

  监督学习模型的数据集必须是有标签的数据，也即这些数据分为($input$)输入数据和($output$)输出数据。而输入数据根据实际应用也有相应的标签($features，属性$​)

1.1.2代码(使用numpy)

import numpy as np
import matplotlib.pyplot as plt

#设置目标函数，用来预测
def predict (x,a,b):
    return a*x+b
    pass

#设置代价函数（损失函数），这里使用误差平方和
def loss(x,y,a,b):
    return np.sum((predict(x,a,b)-y)**2)/2/len(x)
    pass

#计算梯度，更新目标参数a，b
def gradient(x,y,a,b):
    gra_b=np.sum(predict(x,a,b)-y)/len(x)
    gra_a=np.sum((predict(x,a,b)-y)*x)/len(x)
    return gra_a,gra_b
    pass

#进行训练，拟合模型
#tmes单轮训练次数
#alpha每次修正目标参数的步长，即学习步长
#rat，用于判断退出条件，如果相邻两次损失值相差很少，则认为已达到最优
def train(x,y,a,b,times=1000,alpha=0.001,rat=0.000001):
    loss_0=loss(x,y,a,b)
    gra_a,gra_b=gradient(x,y,a,b)
    a_1=a-alpha*gra_a
    b_1=b-alpha*gra_b
    loss_1=loss(x,y,a_1,b_1)
    i=1
    while np.abs(loss_1-loss_0)>rat:
        loss_0=loss_1
        a=a_1
        b=b_1
        gra_a, gra_b= gradient(x, y, a, b)
        a_1 = a - alpha * gra_a
        b_1 = b - alpha * gra_b
        loss_1 = loss(x, y, a_1, b_1)
        i+=1
        if i>times:
            break
        pass
    return a,b
    pass

#准备训练数据
x = np.array([4 ,6, 8, 10, 12])
y = np.array([9 ,11.9, 17, 19, 25])

#开始训练模型
a,b=train(x,y,1,2)
print("模型所预测的参数值为：")
print(a,b)

xx=input("请输入要预测的值大小：")
xx=int(xx)
predict_xx=predict(xx,a,b)
print(predict_xx)


#画原数据集的散点图
plt.scatter(x,y,c='r')
#根据原输入数据画出拟合的直线
plt.plot(x,predict(x,a,b),c='b')

plt.scatter(xx,predict_xx,c='g')
plt.show()
print(predict_xx)

• 运行结果：

  [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wQiV7d6p-1628171812188)(http://m.qpic.cn/psc?/V51vZA5k03lnSi1ptbmb0DEsBj1MBzUA/ruAMsa53pVQWN7FLK88i5t6AXkhdVit0B38tOeyHJlrD7oYJ.dgaNf6JMo.ywYqWf543.MeovA57Ca4xIeTJHn0rKSy*CwRPFQQ6Twce60g!/mnull&bo=gALgAYAC4AEDCSw!&rf=photolist&t=5)]

  [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-x3lbZHfe-1628171812191)(http://m.qpic.cn/psc?/V51vZA5k03lnSi1ptbmb0DEsBj1MBzUA/ruAMsa53pVQWN7FLK88i5t6AXkhdVit0B38tOeyHJlqP68COmLCzreW4jovfR4wXXTAx1lIqLYayZWXL3FytkYFJv2uHxgOiqJOwzosIHgg!/mnull&bo=iQFyAIkBcgADCSw!&rf=photolist&t=5)]

1.1.3正规方程

​ 这是线性模型求解权重矩阵的简便方法。

​ 正规方程表达式如下所示：

​ $\theta ={(X^{T}X)}^{-1}{X}^{T}y$​

• 正规方程的缺陷：特征数量过大($n>1000$​时)计算成本过高

1.2 逻辑回归

• 逻辑回归解决的是二分类问题，它将线性回归拟合的目标函数预测值放到sigmod函数中，即：

  设$z=f(x)$，那么$h=g(z)$为逻辑回归的目标函数。其中：

  ​ $g(z)=\frac{1}{1+e^{-z}}$

  其图像如下所示：

  ​

1.2.1方法步骤

• 确定目标函数

  以$f(x)={\theta }_0+{\theta }_1\ast x$​​​为例，令$z=f(x)$那么目标函数为:

  ​ $h=g(z)$​

  其中：

  ​ $g(z)=\frac{1}{1+e^{-z}}$

• 确定损失函数

  逻辑回归的损失函数使用的交叉熵：

  $J(\theta )=-\frac{1}{m}{\sum }_{i=1}^m[y^{(i)}log(h_{\theta }(x^{(i)}))-(1-y^{(i)})log(h_{\theta }(x^{(i)}))]$

• 梯度下降，更新权重

  根据梯度下降的原理，设置学习步长$\alpha$，根据下式更新各个权重：

  ${\theta }_j={\theta }_j-\alpha \frac{1}{m}{\sum }_{i=0}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$​​

  **注意:**在进行求导时，sigmod函数有一个性质：

  ​ $g^{\prime }(z)=g(z)[1-g(z)]$

• 确定训练数据集、训练次数、训练轮次

  监督学习模型的数据集必须是有标签的数据，也即这些数据分为($input$)输入数据和($output$)输出数据。而输入数据根据实际应用也有相应的标签($features，属性$​)

1.2.2代码(使用numpy)

import numpy as np

#先定义一个sigmod函数
def sigmod(x):
    return 1/(1+np.exp(-x))
    pass

#定义一个目标函数，逻辑回归比线性回归多的就是在线性回归目标函数外面套一层sigmod
def predict(X,w):
    return sigmod(X.dot(w))
    pass

#定义损失函数
def loss(X,w,y):
    py=predict(X,w)
    #由于用到交叉熵，有log项，检查log对数是否为0
    logpy=np.array([0 if p==0 else np.log(p) for p in py])
    logpy1=np.array([0 if 1-p==0 else np.log(1-p) for p in py])
    return np.sum(-y*logpy-(1-y)*logpy1)/len(X)
    pass

def gradient(X,w,y):
    return X.T.dot(predict(X,w)-y)/len(X)
    pass

def train(X,w,y,times=10000,alpha=0.001,rat=0.000001):
    loss_0=loss(X,w,y)
    gra_w=gradient(X,w,y)
    w1=w-alpha*gra_w
    loss_1=loss(X,w1,y)
    t=1
    while np.abs(loss_0-loss_1)>rat:
        loss_0=loss_1
        w=w1
        gra_w = gradient(X, w, y)
        w1 = w - alpha * gra_w
        loss_1 = loss(X, w1, y)
        t+=1
        if t>times:
            break
        pass
    return w
    pass

#设置训练集
trainX = np.array([[ 30, 30, 30],
                   [ 40, 40, 40],
                   [ 60, 62, 62],
                   [ 50, 40, 40],
                   [ 60, 70, 70],
                   [ 90, 80, 80],
                   [ 66, 60, 60],
                   [ 50, 70, 70],
                   [ 60, 50, 50],
                   [ 20, 10, 10],
                   [ 90, 80, 80],
                   [ 33, 33, 33],
                   [ 42, 22, 22],
                   [ 51, 31, 31],
                   [ 80, 70, 70],])
trainY = np.array([0,0,1,0,1,1,1,0,0,0, 1, 0, 0, 0, 1])
#逻辑回归问题必须要对数据集进行归一化，压缩数量级（输出结果仅仅为0，1），否则结果不正确，
trainX = trainX/100
trainX = np.hstack((np.ones(shape=(len(trainX), 1)), trainX))
w=np.array([1,2,3,4])
pw=train(trainX,w,trainY)
print(pw)
testX = np.array([[30, 30, 30],
                  [50, 30, 30],
                  [60, 70, 70],
                  [80, 70, 70],])
testX = testX/100
testX = np.hstack((np.ones(shape=(len(testX), 1)), testX))
py = predict(testX, pw)
print(py)
print(np.where(py > 0.5 , 1, 0))

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
#获取画布
fig = plt.figure()
#设置三维图坐标轴
ax = Axes3D(fig)
x11 = trainX[:, 1]
x22 = trainX[:, 2]
x33 = trainX[:, 3]
#画出拟合的平面，根据训练好的参数
xs, ys = np.meshgrid(np.arange(-3, 3, 0.1),np.arange(-3, 3, 0.1))
z = -(pw[0] + pw[1] * xs + pw[2] * ys )/pw[3]
ax.plot_surface(xs, ys, z, rstride=1, cstride=1)
ax.scatter3D(x11, x22, x33, c='r')
plt.show()

• 模型训练结果：

  [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sKoEjLFT-1628171812192)(http://m.qpic.cn/psc?/V51vZA5k03lnSi1ptbmb0DEsBj1MBzUA/ruAMsa53pVQWN7FLK88i5mHDMjS40VbsWsGxHRpbWXyeUL9uLGvASDdsMzOf13O1fBtvNcks7587mV5X8cwo9VCynwxwRzSgbuNTqOw!/mnull&bo=gALgAYAC4AEDCSw!&rf=photolist&t=5)]

  [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cGrNyKY8-1628171812197)(http://m.qpic.cn/psc?/V51vZA5k03lnSi1ptbmb0DEsBj1MBzUA/ruAMsa53pVQWN7FLK88i5mHDMjS40VbsWsGxHRpbXVelXjknsN78CZp38jd2tuMyYNcFXLDE.jXhRUydL0IkrECWemyons69BYTVdINII!/mnull&bo=*QGpAP0BqQADCSw!&rf=photolist&t=5)]

1.2.3关于多类别逻辑回归

对于多类别逻辑回归，其实质上由多个二分类逻辑回归分类器组成。举例来说：现在要完成一个四分类的逻辑回归分类器，那么首先要对数据集的输出进行one-hot编码。如：现针对学生4门课——数据结构、操作系统、计网、计组进行总成绩评定，一门课都没挂评级为1，仅挂1门评级为2，仅挂2门评级为3，仅挂3门评级为4。

数据结构	操作系统	计网	计组	类别
60	60	60	60	1
60	60	60	59	2
60	60	59	59	3
60	59	59	59	4

那么进行one-hot编码后得到4个数据集：

(1)

数据结构	操作系统	计网	计组	类别
60	60	60	60	1
60	60	60	59	0
60	60	59	59	0
60	59	59	59	0

(2)

数据结构	操作系统	计网	计组	类别
60	60	60	60	0
60	60	60	59	1
60	60	59	59	0
60	59	59	59	0

(3)

数据结构	操作系统	计网	计组	类别
60	60	60	60	0
60	60	60	59	0
60	60	59	59	1
60	59	59	59	0

(4)

数据结构	操作系统	计网	计组	类别
60	60	60	60	0
60	60	60	59	0
60	60	59	59	0
60	59	59	59	1

分别对这4个数据集进行逻辑回归训练，得到4个逻辑回归分类器，在进行预测时，同时输入到这4个分类其中，取预测值最大的那个作为预测结果。

1.2.4正则化与过拟合、欠拟合

(1)过拟合与欠拟合

如下图所示：

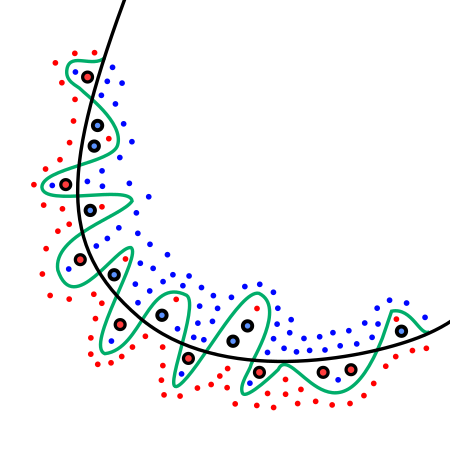
​ 图中的绿色实线即为过拟合现象，这样的模型对于损失函数来说，误差很小，但是模型的方差大，最终的模型预测结果将不会精准。

​ 与过拟合相对应的便是欠拟合，较于过拟合，由于数据不足，模型参数过少或者说模型过于简单，以至于无法捕捉到数据中的规律，此时，模型的偏差大但是方差小。

(2)正则化

正则化的目的便是消除模型的过拟合现象。

现在假设存在这样的数据集$X$​(从图像上看模型可用一个简单二次曲线表示)，对其进行回归，设其目标函数是：

$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1^2+{\theta }_2{x}_2^2+{\theta }_3{x}_3+{\theta }_4{x}_4^3$

代价函数是误差平方和：

$J(\theta )=\frac{1}{2m}{\sum }_{i=1}^m{(h_{\theta }(x^{(i)})-y^{(i)})}^2$​

显然，由于我们增加了4次幂项，使得模型出现了过拟合现象。那么我们可以通过对该模型的代价函数进行修改(添加正则项)来消除过拟合现象。即：

$J(\theta )=\frac{1}{2m}{\sum }_{i=1}^m{(h_{\theta }(x^{(i)})-y^{(i)})}^2+\lambda {\sum }_{j=1}^n{\theta }_j^2$​

• 对于正则化线性回归，我们依旧可以用正规方程来求解，即：

  $\theta =(X^{T}X+\lambda \left[\begin{array}{ccccc}0& 0& 0& 0& \\ 0& 1& 0& 0& \\ 0& 0& 1& ...& \\ 0& 0& ...& 1& \end{array}\right]{)}^{-1}{X}^{T}y$​

• 而对于正则化逻辑回归，其代价函数修改为：

  $J(\theta )=-\frac{1}{m}{\sum }_{i=1}^m[y^{(i)}log(h_{\theta }(x^{(i)}))+(1-y^{(i)})log(h_{\theta }(x^{(i)}))]+\frac{\lambda }{2m}{\sum }_{j=1}^n{\theta }_j^2$

1.3 支持向量机

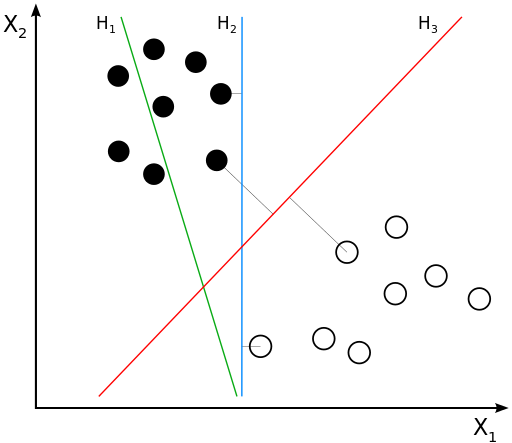
​ SVM(support vector machine)是一个二分类线性分类器，且其模型时定义在特征空间中间隔最大的线性分类器。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RlQqPEvX-1628171812200)(http://r.photo.store.qq.com/psc?/V51vZA5k03lnSi1ptbmb0DEsBj1MBzUA/45NBuzDIW489QBoVep5mcXtmaaYs**zPNbKE2GO1m.dDhyBHUKo5JnYPpnxXUC8Si3D*yvZiU6SkNnwGWYIUwy0NkLMypu.YKColO93nI!/r)]

(1)线性可分SVM

​ 感知机的目标: 找到一个超平面使其能正确地将每个样本正确分类。感知机使用误分类最小的方法求得超平面，不过此时解有无穷多个。

​ SVM向量机的目标：利用间隔最大化求最优分离超平面,这时解是唯一的。

(2)间隔最大化

​ 高数中求两条直线的距离公式推广到高维可以求得:

​ $margin=\rho={2 \over ||W||} $

​ 目标是令$\rho$最大，那么：

​ $\underset{W,x}{\max }\rho ⟺\underset{W,x}{\max }{\rho }^2⟺\underset{W,x}{\min }\frac{1}{2}||W|{|}^2$​

​ 加上约束条件：

​ $X_i^{T}W+b\ge +1,y_i=+1$

​ $X_i^{T}W+b\le -1,y_i=-1$

因此间隔最大化的数学问题就转换为：

​ $\underset{W,x}{\min }J(W)=\underset{W,x}{\min }\frac{1}{2}||W|{|}^2$

​ $s.t.y_i(X_i^{T}W+b)\ge 1,i=1,2,3,...,n$​

(3)支持向量

在线性可分的情况下，训练数据集的样本点中与分离超平面距离最近的数据点称为支持向量(support vector)，支持向量是下列式子：

​ $ y_i(X_i^TW+b) = 1$

的点，也即所有再直线$(X_i^{T}W+b)=1$或直线$(X_i^{T}W+b)=-1$d的点，如下图所示：

​

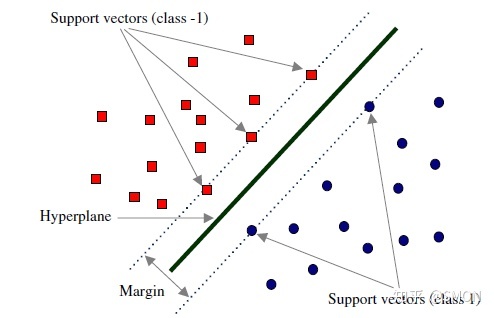
未完待续。。。。。。。。。

2.无监督学习

​ 与监督学习相对的，无监督学习基于无标签的数据集，其目的在于在这些无标签的数据集中挖掘数据之间的关系。

2.1聚类算法

(1)K均值聚类算法

​ K-均值是最普及的聚类算法，算法接受一个未标记的数据集，然后将数据聚类成不同的组。

K-均值是一个迭代算法，假设我们想要将数据聚类成n个组，其方法为:首先选择个随机的点，称为聚类中心（cluster centroids）；对于数据集中的每一个数据，按照距离个中心点的距离，将其与距离最近的中心点关联起来，与同一个中心点关联的所有点聚成一类。计算每一个组的平均值，将该组所关联的中心点移动到平均值的位置。直至中心点不再变化。

​ 该算法是一个迭代算法,其算法的主要步骤包括以下几个步骤：

• 确定优化目标

  在聚类算法中，代价函数也叫畸变函数。因此这一步也叫确定代价函数。

  常见的用于聚类算法的代价函数为:

  $J(c^{(1)},...,c^{(m)},{\mu }_1,...,{\mu }_K)=\frac{1}{m}{\sum }_{i=1}^m||X^{(i)}-{\mu }_{c^{(i)}}|{|}^2$​

  ${\mu }_i$表示聚类中心，$c^{(j)}$用来存储与第j个示例数据最近的聚类中心的索引。

• 随机初始化

  算法开始时，我们需随机初始化所有的聚类中心点。

  先随机选择$K$​个聚类中心点($K<m$).接着随机选择$K$个训练实例，令$K$个聚类中心分别与这$K$个训练实力相等。

  注意：

  (1)K-均值的最大问题在于，算法容易进入局部最优。解决方法就是多次运行算法，再比较多次运行的结果。

  (2)选择聚类数时遵照“肘部法则”，也即畸变函数值下降时的拐点处。

(2)关于聚类算法的相关总结

(1). 闵可夫斯基距离Minkowski/（其中欧式距离：$p=2$)

​ $dist(X,Y)=({\sum }_{i=1}^n|x_i-y_i{|}^p{)}^{\frac{1}{p}}$

(2). 杰卡德相似系数(Jaccard)：

​ $J(A,B)=\frac{|A\bigcap B|}{|A\bigcup B|}$​

(3). 余弦相似度(cosine similarity)：

维向量和的夹角记做，根据余弦定理，其余弦值为：

​ $cos(\theta )=\frac{x^{T}y}{|x||y|}=\frac{{\sum }_{i=1}^n{x}_i{y}_i}{\sqrt[2]{{\sum }_{i=1}^n(x_i^2)}\sqrt[2]{{\sum }_{i=1}^n(y_i^2)}}$

(4). Pearson皮尔逊相关系数：

Pearson相关系数即将、坐标向量各自平移到原点后的夹角余弦。

​ ${\rho }_{XY}=\frac{cov(X,Y)}{{\sigma }_X{\sigma }_Y}=\frac{E[(X-{\mu }_X)(Y-{\mu }_Y)]}{{\sigma }_X{\sigma }_Y}=\frac{{\sum }_{i=1}^n(x-{\mu }_X)(y-{\mu }_Y)}{\sqrt[]{{\sum }_{i=1}^n(x-{\mu }_X{)}^2}\sqrt[]{{\sum }_{i=1}^n(y-{\mu }_Y{)}^2}}$

---

#第二部分 深度学习

一、全连接神经网络

网页链接

1.整体概述

使用5个对象：

• Network神经网络对象=API+层对象+连接对象
• Node节点对象，包含记录连接+输出值+上下游连接+误差项
• Layer层对象，由节点组成
• ConstNode对象，该对象仅针对实现一个输出恒为1的节点
• Connection连接对象记录权重
• Connections提供连接对象的集合操作。由各个集合对象组成

注意 ：在后面有个梯度检查，即检查神经网络运行是否正确。

​ 方法如下：

​ 1.用一个样本d对神经网络进行训练，得到每个权重的梯度

​ 2.$w_{ij}$加上一个很小的值($10^{-4}$),重新计算神经网络在这个样本d下的 $E_{d+}$

​ 3.$w_{ij}$减去一个很小的值($10^{-4}$),重新计算神经网络在这个样本d下的 $E_{d-}$

​ 4.根据下面这个式子：

​ $$\frac{\delta E_d(w_{ij})}{\delta w_{ij}}\approx \frac{f(w_{ij}+\epsilon )-f(w_{ij}-\epsilon )}{2\epsilon }$$

​ 计算出期望的梯度值,和第一步获得的梯度值进行比较，保证他们几乎相同，也即至少4位有效数字相等。

2.反向传播推导

以下图神经网络为例进行推导：

注意：权重矩阵的维度=(后一层单元数，当前单元数)

如此，得到神经网络中各个节点(值)的关系图：

图中所表达的值关系式为：

(2-1)$a^{(1)}=x$​​ (2-2)$z^{(2)}=a^{(1)}{{\Theta }^{(1)}}^T$​​ (2-3)$a^{(2)}=[1,g(z^{(2)})]$​,插入bias项列​

​ (2-4)$z^{(3)}=a^{(2)}{{\Theta }^{(2)}}^T$​ (2-5)$a^{(3)}=[1,g(z^{(3)})]$​，插入bias项列

​ (2-6)$z^{(4)}=a^{(3)}{{\Theta }^{(3)}}^T$ (2-7)$a^{(4)}=[1,g(z^{(4)})]$

• 该网络有4层，input(4+1)–>hide1(3+1)–>hide2(2+1)–>output(1)
• 明确神经网络所使用的代价函数

​ 使用交叉熵作为代价函数，同时进行正则化处理，加上正则项：

​ $J(\theta )=-\frac{1}{m}{\sum }_{i=1}^m{\sum }_{k=1}^K[y_k^{(i)}log({h_{\theta }(x^{(i)})}_k)+(1-y_k^{(}$