解释一下全连接层&CNN中全连接层是什么样的

(名称：全连接。意思就是输出层的神经元和输入层的每个神经元都连接)

在卷积神经网络的最后，往往会出现一两层全连接层，全连接一般会把卷积输出的二维特征图转化成一维的一个向量，这是怎么来的呢？目的何在呢？

举个例子：

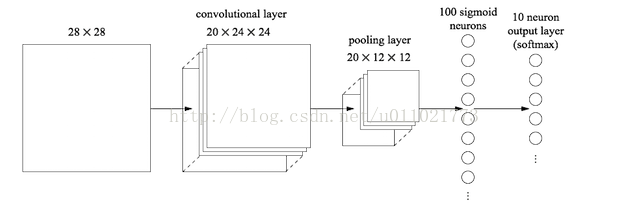
最后的两列小圆球就是两个全连接层，在最后一层卷积结束后，进行了最后一次池化，输出了20个12*12的图像，然后通过了一个全连接层变成了1*100的向量。

这是怎么做到的呢，其实就是有20*100个12*12的卷积核卷积出来的，对于输入的每一张图，用了一个和图像一样大小的核卷积，这样整幅图就变成了一个数了，如果厚度是20就是那20个核卷积完了之后相加求和。这样就能把一张图高度浓缩成一个数了。

全连接的目的是什么呢？因为传统的网络我们的输出都是分类，也就是几个类别的概率甚至就是一个数--类别号，那么全连接层就是高度提纯的特征了，方便交给最后的分类器或者回归。

但是全连接的参数实在是太多了，你想这张图里就有20*12*12*100个参数，前面随便一层卷积，假设卷积核是7*7的，厚度是64，那也才7*7*64，所以现在的趋势是尽量避免全连接，目前主流的一个方法是全局平均值。

也就是最后那一层的feature map（最后一层卷积的输出结果），直接求平均值。有多少种分类就训练多少层，这十个数字就是对应的概率或者叫置信度。

---------------------------------------------------------------------

CNN中全连接层是什么样的？

名称：全连接。意思就是输出层的神经元和输入层的每个神经元都连接。

例子： AlexNet  网络中第一个全连接层是这样的：

layer {
  name: "fc6"
  type: "InnerProduct"
  bottom: "pool5"
  top:"fc6"
  param {
    lr_mult: 1
    decay_mult: 1
  }
  param {
    lr_mult: 2
    decay_mult: 0
  }
  inner_product_param {
    num_output: 4096
    weight_filler {
      type: "gaussian"
      std: 0.005
    }
    bias_filler {
      type: "constant"
      value: 0.1
    }
  }
}

其中  bottom: "pool5"就是这个全连接层的输入，而top:"fc6"就是这个全连接层的输出。值得注意的地方是这个bottom: "pool5"是个“二维平面“式的数据，也就是N X M的数组样式，但是top:"fc6"确是一个K X 1或者 1 X K的向量，因此在实现中，程序会将bottom: "pool5"拉成N*M X 1或者1 X M*N的向量。

这个输入向量是什么呢？对，是特征图，符号化就是X(1)、X(2)、X(3)...X(N*M)，括号内是X的下标。

那么输出呢？如果这个全连接层不是最后一个全连接层那么它也是特征图，符号化就是Y(1)、Y(2)、Y(3)...Y(K)，括号内是Y的下标。

那么输入和输出是怎么联系到一块呢？答案就是W权重了，也叫滤波器，也叫卷积核。

那么在全连接层里怎么没看到这个滤波器的大小呢？答案是：不需要，因为它就是全连接啊。

一般情况下，输入神经元的个数不等于输出神经元的个数，那数目不等的输入输出神经元怎么连接起来呢？还有，这个滤波器（卷积核）是什么样呢？可以看看下面例子：

其中(X_1,X_2,X₃)就是输入神经元（特征图），而(Y₁Y₂)就是输出神经元（特征图），两层之间的连接就是卷积核：，想想矩阵相乘，就明白1X3的“矩阵”怎么变成1X2的矩阵了。

总的下来就是：，

这个卷积核的形状是在代码中自动计算出来的。