引子
后台收到了很多留言问我这个抄底指标到底怎么用?
然后还有人问我,列这么多数据出来有有什么意义?
还有一个老铁问为什么那个房地产最近涨的这么高,对小白有什么指导意义?
好的,我现在来回答这三个问题。
先来回答第三个问题,这个老铁是在8月2号去看的7月14日的表,算是他乌龙了。
我推测他想说的是,“地产都长老高了,为啥那个指标还排在第一位。”
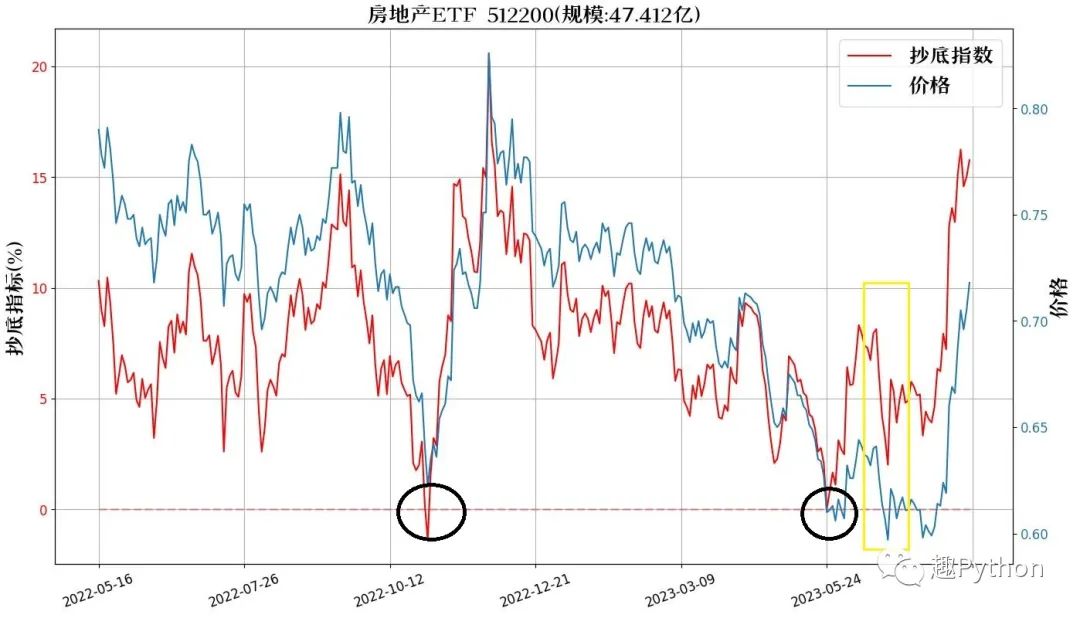
哈哈哈,7月14日的时候(下图黄色方框处),地产可是在低位哦。
不放心的同学可以去翻一下【512200房地产ETF】的K线。
列这么多数据出来有有什么意义?
数据是程序跑出来的,仅供参考,盈亏自负。
再来白话解释下这个指标,拖了很久,抱歉各位。
正文
嗯,我们来说说原理。
数学上很有名的数据分布,叫正态分布,又叫高斯分布,这个学数学的人应该都知道啊。
但是我今天不想把这个它的详细的理论和特性跟大家分享。
我只是讲一讲这个基本原理。
正态分布又叫常态分布,它简单来说的意思就是说,在常规的情况下,所有的事物都会服从这个规律。
“数学定义:
若随机变量服从一个数学期望为μ、方差为σ²的正态分布,记为N(μ,σ²)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ=0,σ=1时的正态分布是标准正态分布。
”
嗯,然后呢,从数学上来讲啊,有其他的一些各种各样的什么分布啊,像什么瑞丽分布,阿尔法分布,伽马分布,等等,都可以看到是这个正态分布的一个变式,今天就不给大家掉那个数学的书袋子了啊。

举两个例子,以身高为例,就是说正常情况下吧,个子非常高和个子非常矮的人都非常少,对吧。
然后大部分人都集中在一个中间那个区间,对吧;超过两米的人,肯定都很很少对吧;然后呢,低于比如说一米二的人,肯定也很少对吧。
再比如呢,像这种智商,也是一样的,特别聪明的人很少对吧,然后那个智商低的人也很少,大部分人,智商都是正常的对吧。
如果把这些数据统计出来,你就会发现它就是正态分布,它的形状像是一个倒扣的钟。
正态分布它有两个参数,一个叫做期望,叫做标准差。
期望简单理解,它是平均最中间的那个平均值。
然后标准差呢,就表示它的一个形状。
形状就是它的那个胖瘦,如果标准差比较大的话,它就很矮很胖;然后如果标准差比较小的话,它就很尖很瘦。
那么正态分布有一个什么特性呢?
一个数据,它落在均值的一个标准差之内的概率大概在68.3%,落在两倍的标准差的范围内的概率是95.5%。
好,到这里就够了!
就是说落在两倍标准差内的概率是95%,
也就是说它落在两倍标准差之外的概率也就是大约4%。
对吧。
薛斯通道,它有四根线,它的原理跟这个正态分布上面说的特性的这个原理,是类似的啊。
它不能说一模一样,它简直就是一模一样。
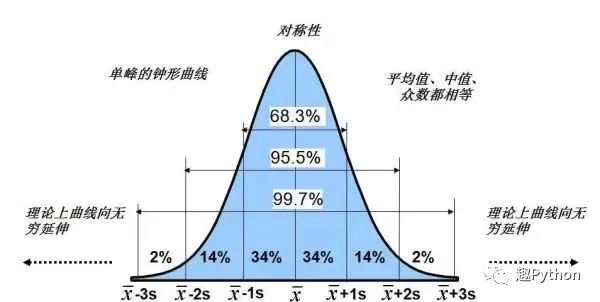
回到那个ETF的价格,因为ETF大概是一个行业相关的一个平均值,对吧,那么它的价格跌到两个标准差之下的概率和涨到两个标准差之上的概率,都不会超过2%,对吧。
那么它是什么意思呢?
就是说啊,你跌落到这个两倍标准差之下概率也很小,对吧,很小的意思就是什么意思呢?
就大概它这个底,对吧,或者它大概是个顶,对吧。
这个就是它的一个很基本的一个数学原理,
当然我没有去找这个严格的一个数学推算啊,但是它的基本原理是这个样子的。
好,那现在我给大家来说第二个问题,
就是为什么把这个数据都列出来。
我这里统计的是市面上所有的ETF,只是给大家做一个数据的一个展示,我把它的值做一个很简单的,极简的量化,大家能看的很清楚。
当然这个指标也只是它的一个方面,对吧。
从数学的角度来说它也不是100%的对,但是它大概率是对的,对吧,因为它是一个概率算出来的,所以,你去实际做操作的时候,按我的理解啊,还是要去考虑一下当前的市场情况,对吧。
如果情绪很高的,它可能会往上过头对吧,如果情绪很低落,它有可能下跌过头,对吧,所以要结合当前的市场的情况来做一些些判断。
然后呢,最后一个问题,就是说房地产这个指标的问题。
我刚好把房地产的这个数据拉出来了,见上面的那个图,这个图是最近一年的数据,大家可以很直观的看到它的一个走势啊。
红色的线是薛斯通道的最底下的那根线,也可以理解为小于均值的2倍标准差的数据,当它为0,或者小于0的时候,我们就可以搞点事情,对吧。
蓝色的那根线是价格。
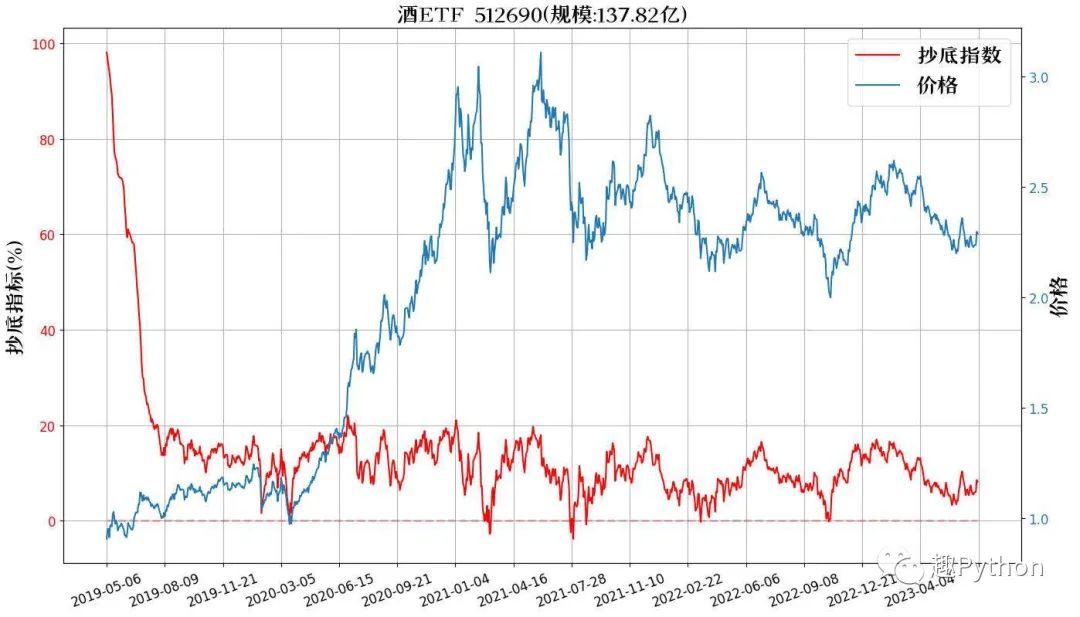
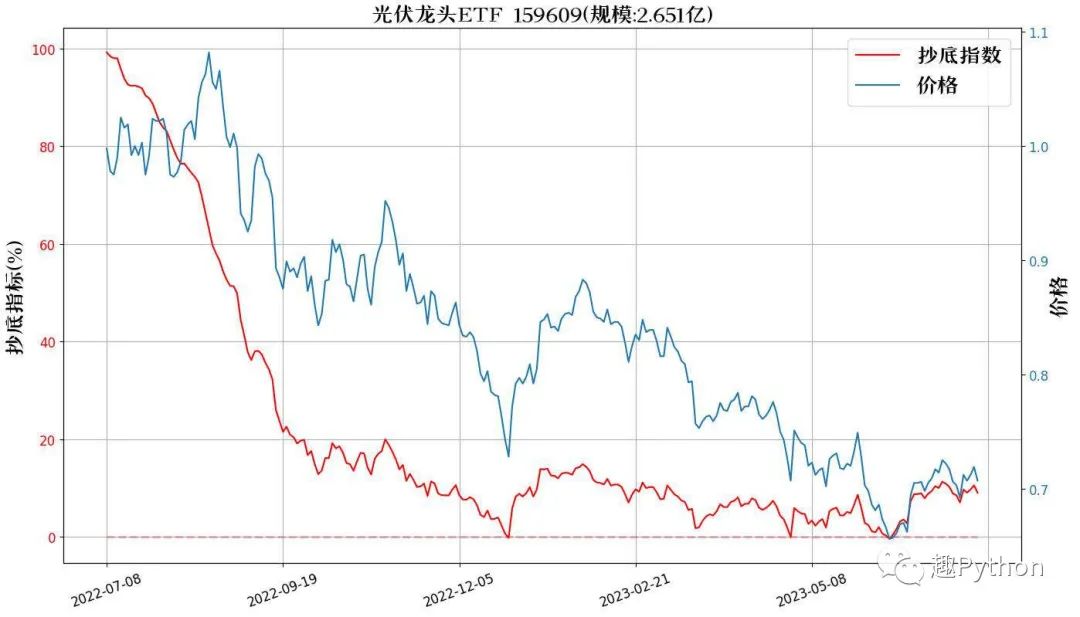
对ETF数据来说,成立时间越久,收敛性越好。
最后再贴2个数据,大家感受下。
最后
本文,
是抽空用手机语音录的,所以有很多对吧,对吧之类的口语,大家能理解就好。
有时候写起来也真是挺累的,想想要不要整点付费啥了。
后来想想还是算了。
老铁们没事看完文章顺手点一下文末的广告,让腾讯大哥给我多发点广告费,
谢谢各位。
本文所有数据图表均由作者Python程序而来,实属不易!~~
请帮忙点赞,分享和在看,点点文末广告,谢谢!~
如有低频量化的交流,请留言,谢谢!~
























 1588
1588

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








