1.2贝叶斯决策

贝叶斯决策

分类器

贝叶斯决策是属于基于统计决策的分类器

无论分类器原理如何复杂，都可以表示为一个多元单值函数
$$F(x):X^d\to Y[-1,1]$$

贝叶斯决策在什么场景下使用？

前提：目标(事物)的观察值是随机的，服从一定的概率分布。

贝叶斯决策能够用于分类的出发点是什么？

贝叶斯决策思想及计算公式

由事件(样本)→现象(特征)→推断事件及其概率，例子:男性女性样本→身高、体重→生成分类器分类(给新的样本比如身高177cm体重75kg判定属于男性)

后验概率的计算(Bayes公式)：$$P({\omega }_i|X)=\frac{P({\omega }_i)p(X|{\omega }_i)}{P(X)}=\frac{P({\omega }_i)p(X|{\omega }_i)}{\sum _{i=1}^{M}P({\omega }_i)p(X|{\omega }_i)}$$

一些基本概念

几种常用的决策规则

1.基于最大后验概率的贝叶斯决策(MAP)

决策规则(属于那类的后验概率最大，即判断为哪一类)
$$argmaxP({\omega }_i|X)$$
判别函数 ：$$g_i(x)=P({\omega }_i)p(X|{\omega }_i)$$

2.基于最小错误率的贝叶斯决策

$$minP(e)=\int P(e|x)p(e)dx$$
二分类时等价于最大后验贝叶斯决策

3.基于最小风险的贝叶斯决策

考虑不同错误所带来的损失(相当于对每一项决策赋予权重)--------决策使风险最小

1.把样本$x$看作$d$维随机变量$x={\left[\begin{array}{cccc}{x}_1,& x_2,& ...& x_d\end{array}\right]}^T$
2.状态空间$\Omega$由$c$个可能的状态组成： Ω = { ω 1 , ω 2 , . . . ω c } Ω=\{ ω_1,ω_2,...ω_c \} Ω={ω1​,ω2​,...ωc​}
3.对随机向量$x$可能采取的决策组成了决策空间，由$k$个决策组成： A = { a 1 , a 2 , . . . a k } A=\{a_1,a_2,...a_k\} A={a1​,a2​,...ak​}
4.对于实际状态${\omega }_j$的向量$x$，采取决策$a_i$所带来的损失为$\lambda (a_i,w_j)$，形成损失函数(权重)（人为确定）

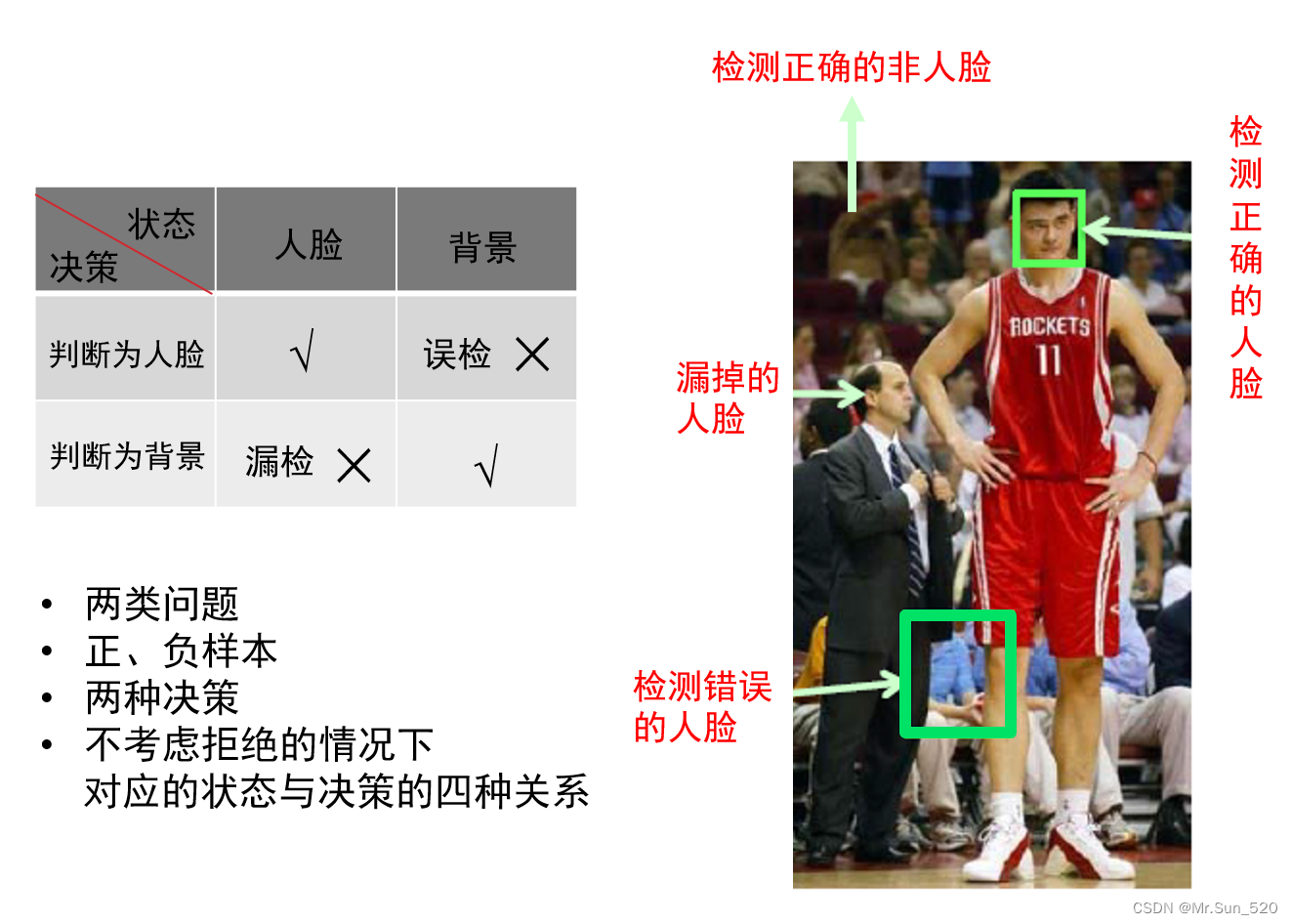
判别？

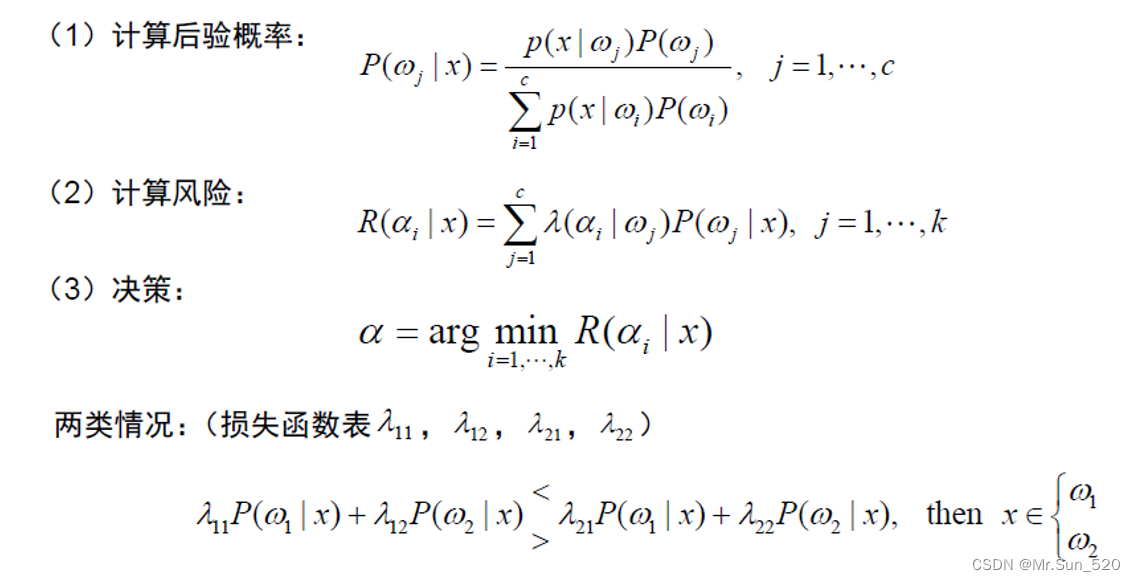
两类错误率

真阳性率(True Positive Rate, TPR):$$\frac{TP}{TP+FN}$$
假阳性率(False Positive Rate, FPR) :$$\frac{FP}{FP+TN}$$
查准率P：$$\frac{TP}{TP+FP}$$
查全率R：$$\frac{TP}{TP+FN}$$

针对同一个分类器，根据真阳性率和假阳性率画ROC曲线，用曲线下的(相对)面积即AUC(area underROC curve)来定量地衡量方法的性能

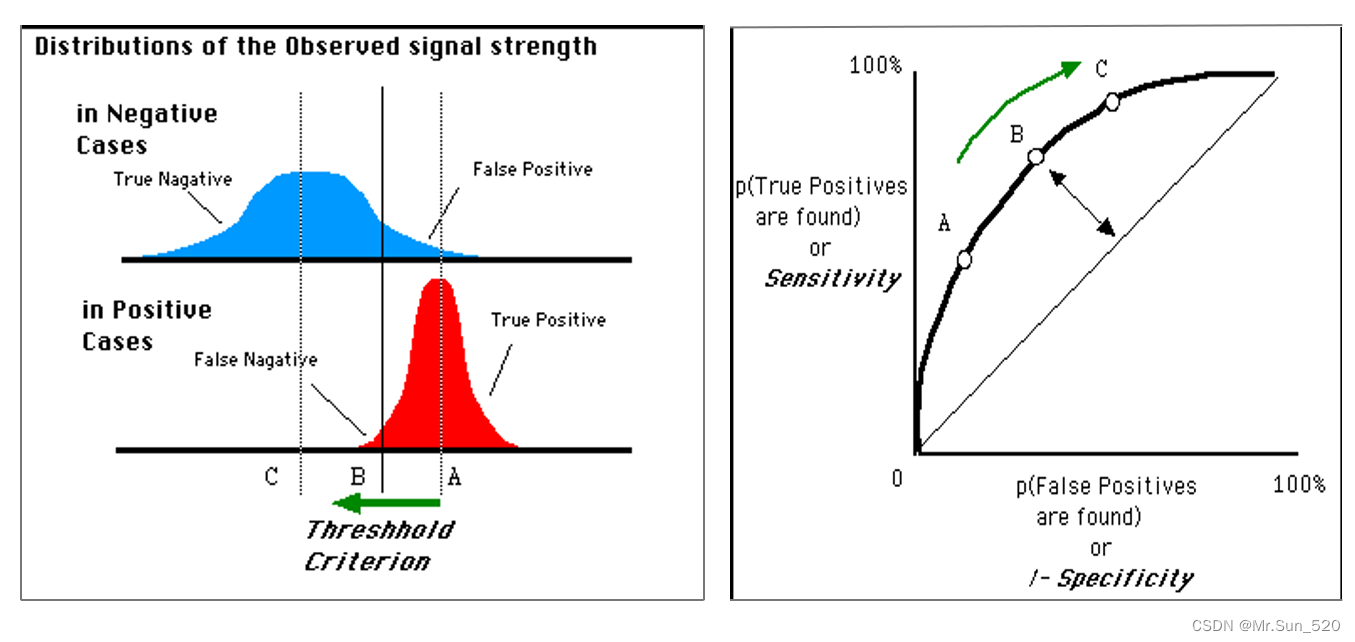
根据查准率和查全率画PR曲线，找到针对自己需求(如更需查全且查准率大于80%)下对应参数为分类器参数，或选择最优分类器