打开深度学习的锁
导言
本篇知识背景来源于吴恩达教授的DeepLearning课程作业–第二节,有兴趣的同学可以自行搜索。
博客所用到的数据集和测试代码已经公开:Github
最后一次修改:2023/12/04(在每一个章节后面添加“核心知识点”方便理解)
这篇博客本质内容吴恩达教授的DeepLearning的课程作业第二节,是题解。个人觉得作为神经网络入门练习是一个很棒的契机,故以此记录。
博客中包含一点Python向量化(Vectorization)和导数(Derivative)及链式法则(Chain rule)的内容,如果看不明白也没关系,别紧张也别怕。只需要明白以下的内容即可:
1.Python向量化(Vectorization): 一种技术,就是代替Python的for循环,跑的比for循环快。
2.导数(Derivative)及链式法则(Chain rule): 如果你知道 ?+A=B也就是知道"A增加导致B增加",它可以告诉我们它们之间是如何互相影响的。
这篇博客中用到的主要是NumPy库中的函数,但是我不会详细的去讲解每一个函数的功能,就是使用。
还有一点很重要,如果你是科班,之前只是说过“机器学习”、“深度学习”、“模型”这类词汇,感觉中间的处理很黑盒,但是不了解到底是什么。
那么这些很重要:
所谓模型:是由很多同类型的数据产生的一个(组)参数适合(W和b) 的函数,得到这个函数,方便处理其它同类型数据。
模型不是软件!不是软件!不是软件!
所谓学习:通过数据的输入–>得到模型的预测值,将预测值和实际的标签比较,标签和预测值的差异称为损失。通过之间的损失自动调整公式里面参数,最终找那个可以让损失最小的、合适的公式的参数!
不是单纯的输入数据和输入的标签学习映射关系!
好了,让我们开始吧。
前置1:神经网络的训练过程
放此图在这里为了快速认识,也为了需要的时候快速查找。初次看的时候看不懂没关系,可以先看下面的内容。
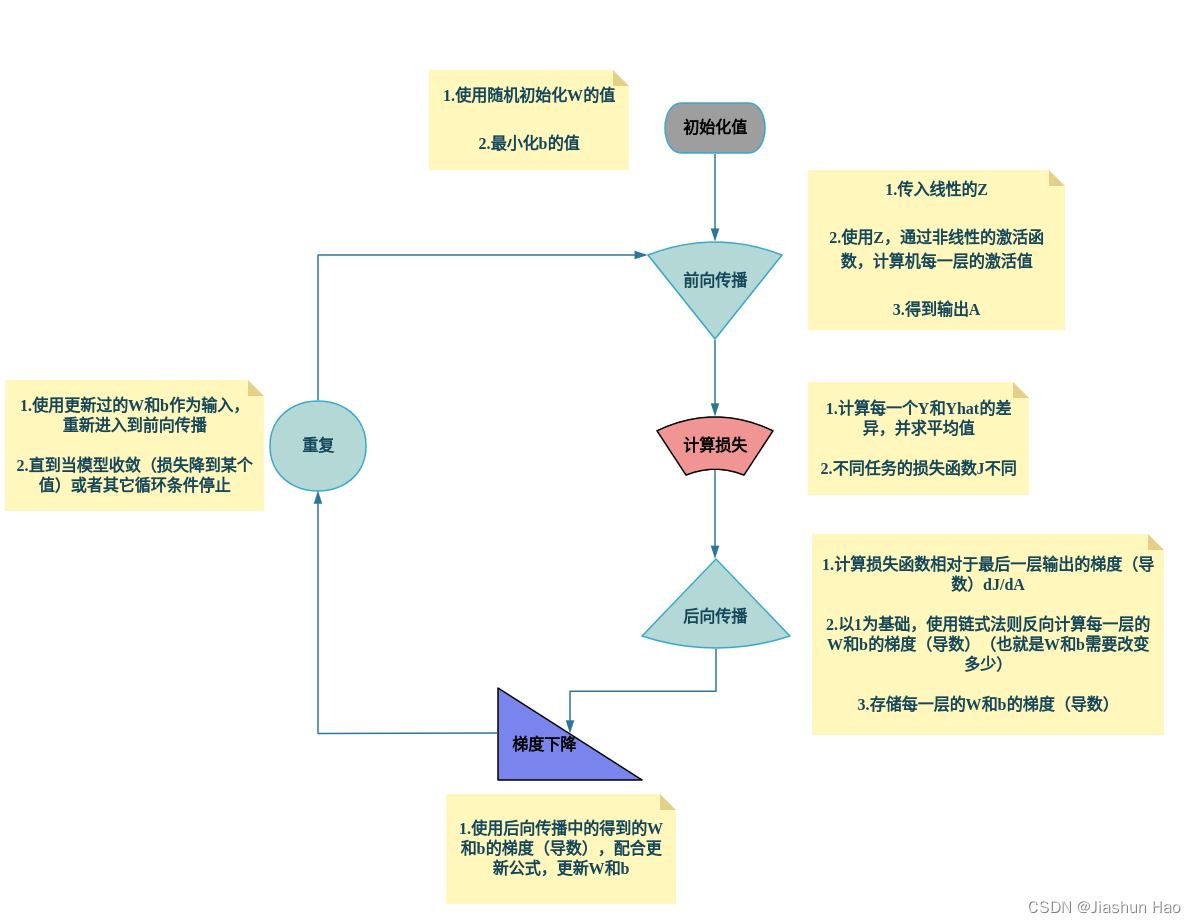
前置2:代码编写过程
1:导入包和工具类,提取工具类
2:数据初始化部分
3:构建sigmoid函数
4:构建初始化函数,初始化w和b
5:构建传播函数(前向和后向)
6:构建最小化(优化)函数 / 剃度下降
7:构建预测函数
8:整合和画图
一、导入的包和说明
关于头文件的说明:
#1.导入序列化必要函数
import numpy as np
#2.导入生成图片要的包
# 在 Python 中导入 matplotlib 库的 pyplot 模块并为其指定一个简称 plt 的语句。matplotlib 是一个非常流行的 Python 数据可视化库,它提供了一套全面的绘图工具来制作各种静态、动态或交互式的图形。
# pyplot 是 matplotlib 的一个子模块,通常被认为是该库的核心。它提供了一个类似于 MATLAB 的绘图界面,使得创建图形变得非常简单。
import matplotlib.pyplot as plt
#导入针对数据格式的包,本篇中用到的数据集格式是.h5.
# h5py 是一个 Python 库,它提供了一种高效的方式来读取和写入 HDF5(h5) 格式的文件。
# HDF5(Hierarchical Data Format version 5)是一个流行的数据存储格式,常用于大型数据集,如科学计算或深度学习中的训练数据。
# HDF5 文件可以包含大量的数据集并支持高效的并行IO操作,它提供了一种结构化的方式来存储数据,其中数据可以被组织为不同的组和数据集。
import h5py
#从lr_utils文件(或者称为模块,每一个py文件就是一个模块)导入函数
from lr_utils import load_dataset
二、数据的预处理
2.1 数据集说明
在给出的文件lr_utils 中的load_dataset函数是对训练集和测试集的预处理,并且已经封装好了
import numpy as np
import h5py
def load_dataset():
train_dataset = h5py.File('datasets/train_catvnoncat.h5', "r")
train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
#保存的是训练集里面的图像数据(本训练集有209张64x64的图像)。
train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels
#保存的是训练集的图像对应的分类值(【0 | 1】,0表示不是猫,1表示是猫)。
test_dataset = h5py.File('datasets/test_catvnoncat.h5', "r")
test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
#保存的是测试集里面的图像数据(本训练集有50张64x64的图像)。
test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels
#保存的是测试集的图像对应的分类值(【0 | 1】,0表示不是猫,1表示是猫)。
classes = np.array(test_dataset["list_classes"][:]) # the list of classes
#保存的是以bytes类型保存的两个字符串数据,数据为:[b’non-cat’ b’cat’]。
train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes
我们直接在主文件里面使用即可
import numpy as np
import matplotlib.pyplot as plt
import h5py
from lr_utils import load_dataset
#全局变量
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes=load_dataset()
现在,我们拥有了数据集和测试集合,可以使用X.shape的方法查看一下它们的维度
print(train_set_x_orig.shape) #(209, 64, 64, 3) 维度说明:训练数据集是由209个 64*64的3色域图片组成
print(train_set_y_orig.shape) #(1, 209) 标签,1维度的209个标签
我们注意到训练集是一个(209,64,64,3)维度的矩阵,那么这个是什么呢?
其实就是保存的209个,大小为64*64像素的RGB的图片
举个例子:

这里有一条可爱的猫猫的图片,假设它的大小是 5*5 个像素。(图片来源:图片)
我们知道,每一个图片在计算机中存储的形式都是由红色(R)、绿色(G)、蓝色(B)三个底色图片构成
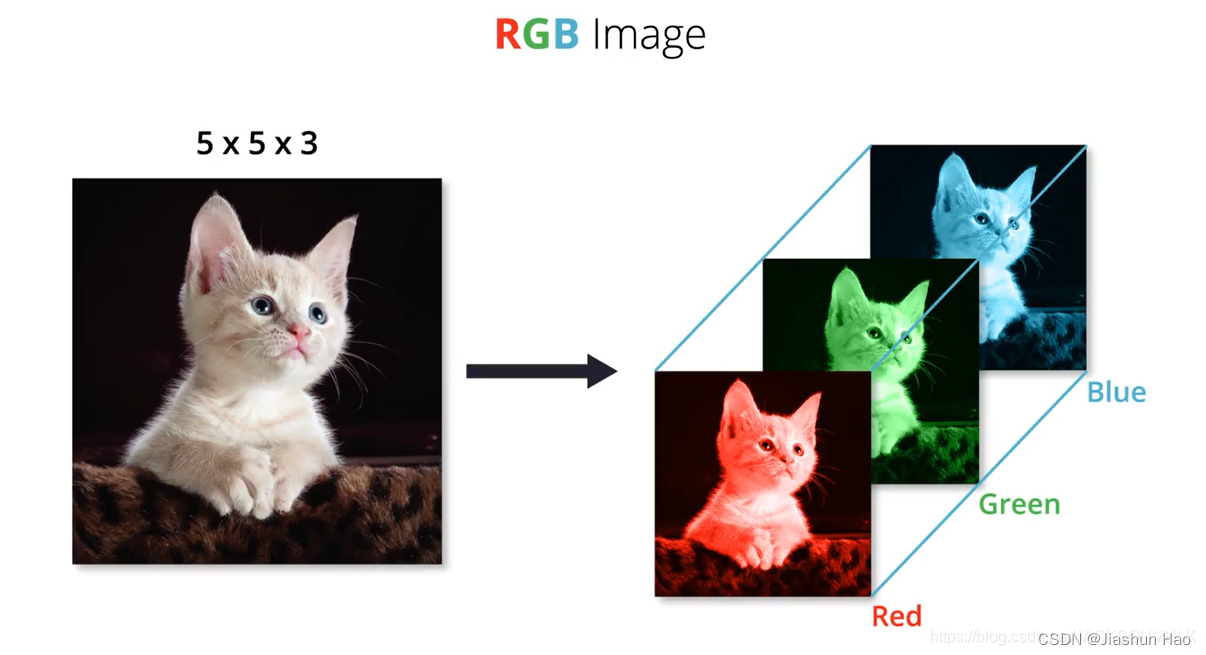
这三个底色图片的参数都不一样,因为不一样,所以才可以构成千颜万色。
对于当前的步骤,我们不需要关心每一个矩阵中的参数是怎么样的。
我们只需要知道,一个图片,在计算机中完整的像素的个数是:高像素 X 宽像素 X 3
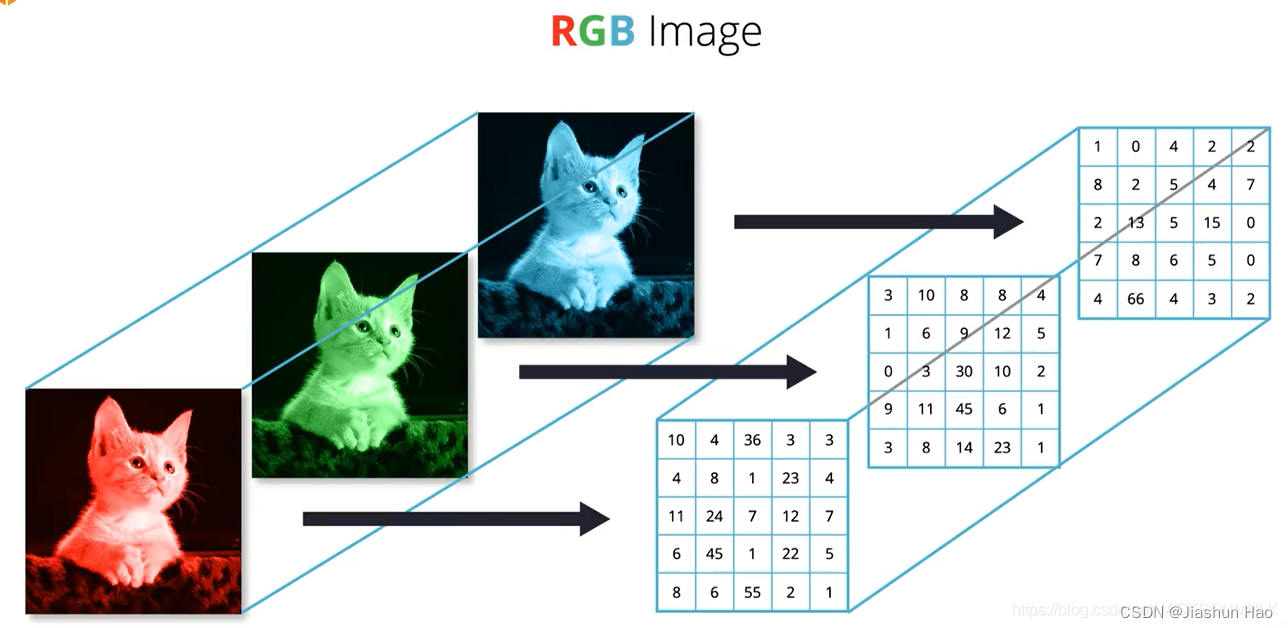
所以,一个图片的矩阵向量的表现形式就是 [ 高像素 , 宽像素 , 3 ] ,这条猫猫的矩阵向量的表现形式是[5,5,3]
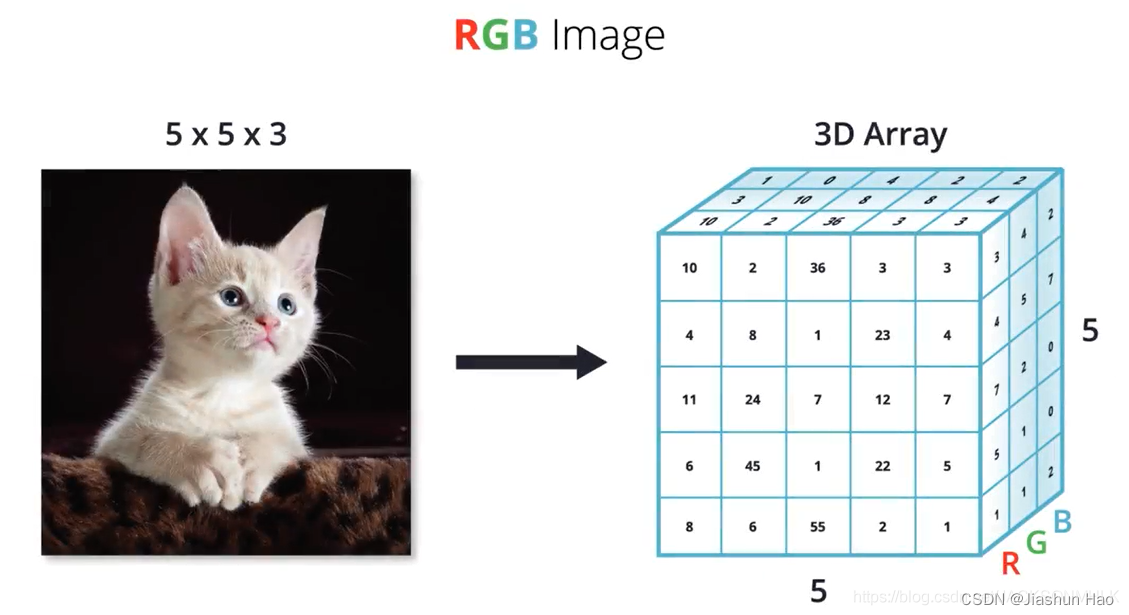
而在本题中,作为数据集,自然要有样本的个数,所以我们的train_set_x_orig矩阵多了一个209,代表样本的个数。
print(train_set_x_orig.shape) #(209, 64, 64, 3) 维度说明:训练数据集是由209个 64*64的3色域图片组成
为了证明我没有胡说,我们打印两个数据集中的图片看看
第一个:高贵的瓦坎达吉祥物
#打印测试单个
index=25
plt.imshow(train_set_x_orig[index])
plt.show()
# print("label:"+str(train_set_y_orig[:,index]))
第二个:非猫
#打印测试单个
index=26
plt.imshow(train_set_x_orig[index])
plt.show()
# # print("label:"+str(train_set_y_orig[:,index]))
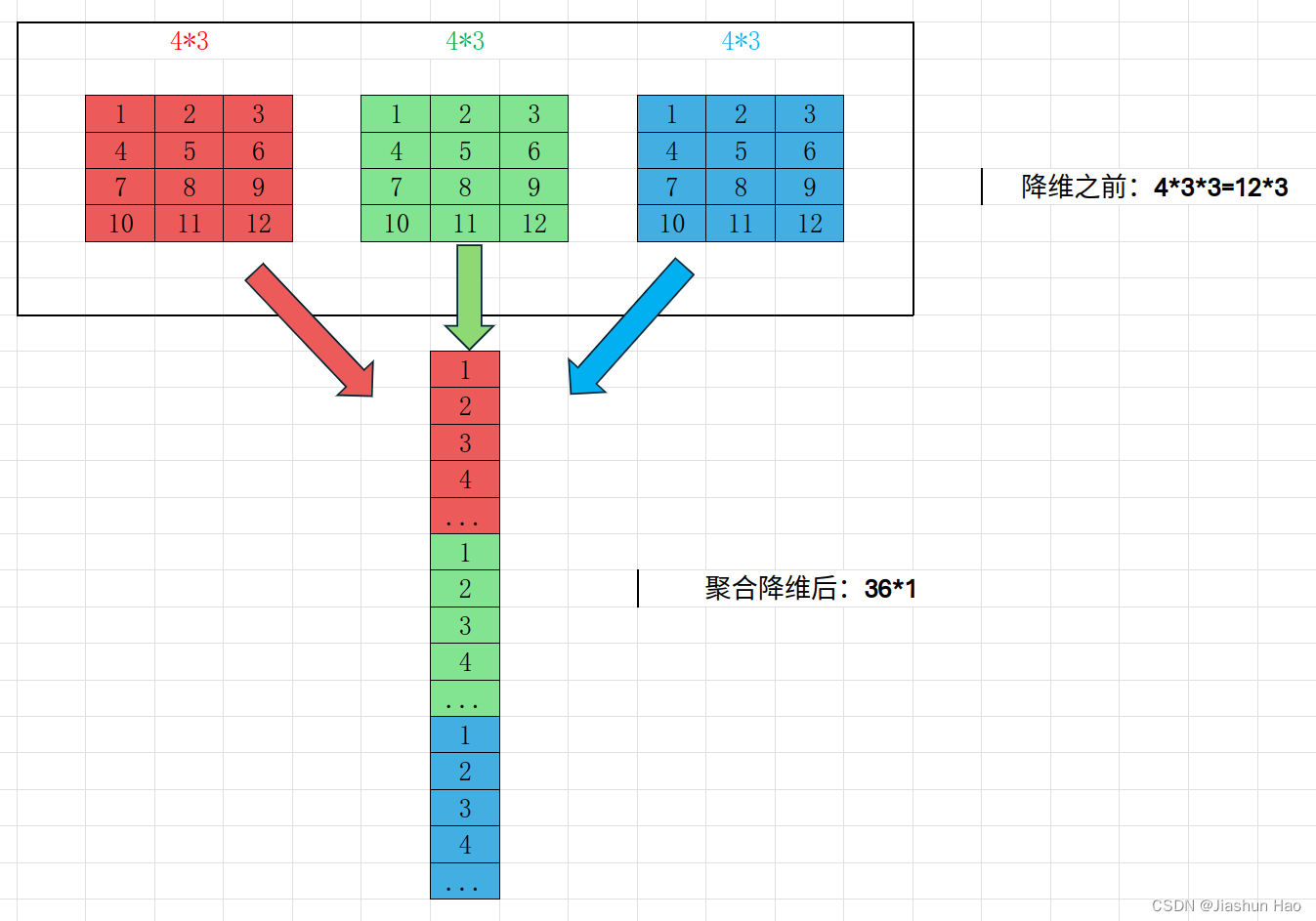
2.2 数据集降维度并且转置
好了,将接下来我们需对于数据集降维度并且转置。
或者换句话说,我们希望聚合每一个对象(此题为每一张图片)的多维度的特征(此题为图片的三原色特征)
这样的做法可以让数据的输入变得容易一点。
此外,我们刚刚提到的,测试了两个数据集合的维度,可以看到它们是不匹配的:
根据矩阵先行数后列数,我们可以看到样本是一个 209 X64X64X3的四维矩阵,而标签则是一个1行209列的二维矩阵。
print(train_set_x_orig.shape) #(209, 64, 64, 3)表示样本个数的209在第一维度,之后有三个维度的数据。
print(train_set_y_orig.shape) #(1, 209) 表示标签个数的209在第二个维度,之前有一个维度的数据。
所以,为了方便数据输入到模型,我们希望统一训练集和测试集的格式
即我们希望将第一个数据集的格式,转化成和第二个数据集合一样的个格式。
我们的目的是希望将 A(a,b,c,d) 的矩阵变成 A(b * c * d , a) 矩阵,公式为:
X_flatten =X.reshape(X.shape[0],-1).T
代码如下:
#Dimensionally reduce and Transpose the Training Data_set
# print(train_set_x_orig.shape) #(209, 64, 64, 3)
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0],-1).T
# print(train_set_x_flatten.shape) #(12288, 209)
#Dimensionally reduce and Transpose the Testing Data_Set
# print(test_set_x_orig.shape) #(50, 64, 64, 3)
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0],-1).T
# print(test_set_x_flatten.shape) #(12288, 50)
下一步,我们希望标准化数据,将每一行的 值 控制在0-1之间。标准化的方法有很多,但是因为所有的都是图片的RGB,所以可以直接除以255
train_set_x=train_set_x_flatten/255
test_set_x=test_set_x_flatten/255
这个时候有小朋友就会问了:“ 前面不是已经将除了”个数“以外的数据都相乘了吗?只除以一个255够了吗?”
当然,因为reshape 函数允许我们重新组织数组的维度,但它 不会 更改数组元素的顺序或值。
也就是说,只是维度被整合了,元素里面的值和内容还是没有改变。
并且,我们都知道在矩阵计算中乘除一个数就算对矩阵内的所有元素进行乘除,所以只写一个/225就够啦!
2.3 数据预处理完整代码
#获取数据集
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes=load_dataset()
# 打印测试单个
index=25
plt.imshow(train_set_x_orig[index])
plt.show()
# print("label:"+str(train_set_y_orig[:,index]))
#降维度
# print(train_set_x_orig.shape) #(209, 64, 64, 3)
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0],-1).T
# print(train_set_x_flatten.shape) #(12288, 209)
#Dimensionally reduce and Transpose the Testing Data_Set
# print(test_set_x_orig.shape) #(50, 64, 64, 3)
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0],-1).T
# print(test_set_x_flatten.shape) #(12288, 50)
#将每一行的值控制在0-1之间,因为所有的都是图片的RGB,所以可以除以255
train_set_x=train_set_x_flatten/255
test_set_x=test_set_x_flatten/255
三、逻辑回归概念以及函数
数据处理的部分完成了,接下来就是构建神经网络。我们要处理的是二分类问题,而 “逻辑回归” 是处理二分问题的一个算法。
逻辑回归的目标:逻辑回归是判断事情发生的可能性,进一步说明,就是分类任务。判断哪些事情可能发生、哪些事情会发生(二分类任务)。
具体到实际功能,逻辑回归的目标是是找到一个决策边界,然后根据样本点相对于这个边界的位置来分类,对于线性逻辑回归,这个决策边界是一条直线(在二维空间中)或一个超平面(在更高的维度中),这取决于特征的数量。
就是说,找一条线,将数据划分为两个部分。
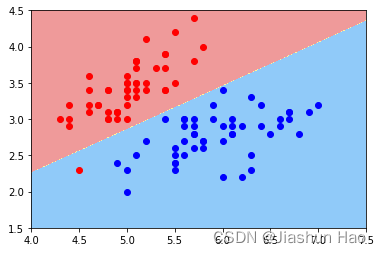
如果维度高的话,是找一个面来划分
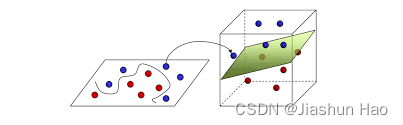
对于逻辑回归的函数,我们可以理解为:
逻辑回归函数=线性回归函数 + sigmoid函数
3.1 线性回归函数公式
Z = z ( i ) = w T ⋅ x ( i ) + b Z = z^{(i)} = w^T \cdot x^{(i)} + b Z=z(i)=wT⋅x(i)+b
- x i x^i xi: 第i个样本的特征向量
- w: 权重向量,表示当前 x i x^i xi的权重比(权重用于决定决策边界怎么画)
- w.T: 是w的转置,我们为了计算w与x的“点乘”,要求w的行向量 == x的列向量.如果你的 w 向量本来就是一个行向量,并且它的长度(列数)与 x 向量的长度(行数)相同,不需要再进行转置,但是,权重向量和特征向量通常都被定义为列向量,这是一种约束。
- b: 这是偏置项,它是一个常数。
- z i z^i zi: 第i个样本的线性输出。输入一个 x i x^i xi,会得到一个 z i z^i zi
3.2 sigmoid函数
为什么要加入sigmoid函数呢?因为线性函数的变化单一,无法完成多样的任务。为了达到这个目的,我们通常将线性函数与其它函数结合使用,达到“二次变化”。sigmoid就是“其它函数”中的一个,处理二分类很好。
公式如下:
σ
(
z
)
=
1
1
+
e
−
z
\sigma(z) = \frac{1}{1 + e^{-z}}
σ(z)=1+e−z1
补充:“z” 就是经过线性函数计算以后得到的结果,在代码编写中直接向sigmoid传入线性函数和参数
嵌套线性回归函数公式:
y
^
i
=
1
1
+
e
−
(
w
T
⋅
x
(
i
)
+
b
)
\hat{y}^i = \frac{1}{1 + e^{-( w^T \cdot x^{(i)} + b)}}
y^i=1+e−(wT⋅x(i)+b)1
关于sigmoid函数,我们需要知道:
- 它是一种激活函数,激活函数是神经网络中的一个重要组成部分,它决定一个神经元是否应该被“激活”或“触发”。具体地说,激活函数定义了每个神经元的输出与其输入之间的关系。它为神经网络引入了非线性因素,使得网络能够学习并执行更复杂的任务。
- 它的输出范围:[0,1]
- 它的图像是这样:
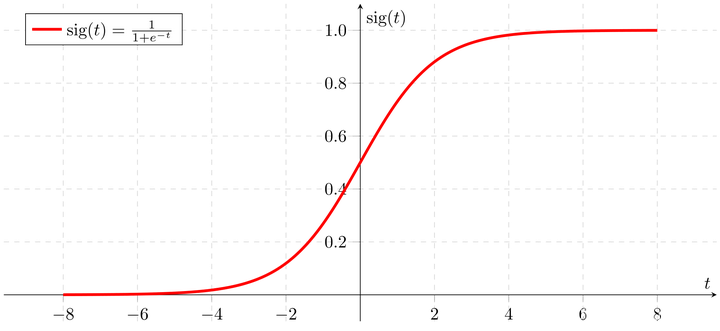
当我们将一个 x i x^i xi输入到sigmoid函数中,会得到一个 y ^ \hat{y} y^或者 y ^ i \hat{y}^i y^i ,它是由 x i x^i xi生成的和当前标签 y i y^i yi同类型的值(这也是为什么用hat/y表示而不是用别的字母)
它是0和1之间的概率值,表示正类(也就是1)的预测概率。
在这里, y ^ i 是模型对输入 x i 的预测输出,而 y i 是实际的标签或真实值。 \text{在这里,} \hat{y}^i \text{ 是模型对输入 } x^i \text{ 的预测输出,而 } y^i \text{ 是实际的标签或真实值。} 在这里,y^i 是模型对输入 xi 的预测输出,而 yi 是实际的标签或真实值。
我们希望 x i 生成的预测 y ^ i 尽可能接近 x i 的标签 y i 。 \text{我们希望 } {x}^i \text{ 生成的预测} \hat{y}^i \text{尽可能接近 }{x}^i \text{的标签 }y^i \text{。} 我们希望 xi 生成的预测y^i尽可能接近 xi的标签 yi。
为了得到一个明确的分类预测(0或1),可以设定一个阈值,通常为0.5。如果 y ^ \hat{y} y^大于0.5,则预测为1,否则为0。
所以,在这个公式中,为了让 y ^ \hat{y} y^ 趋近于1,我们便需要让 w T ⋅ x ( i ) + b w^T \cdot x^{(i)} + b wT⋅x(i)+b的值尽可能的大。
所以,逻辑回归的目标,就是找到合适的 w w w和 b b b
好了,概念理清了,我们开始写代码
对于代码,关于线性函数我们一会可以使用np里面的函数直接计算,所以只需要写sigmoid的函数即可:
def sigmoid(z): #z:传入的线性函数的结果值
s=1/(1+np.exp(-z))
return s #$\hat{y}$
下一步,既然要找 w w w和 b b b,我们就应该写一个初始化函数先给 w w w和 b b b 赋默认值。
四、初始化函数
核心知识点:
1: random 指定了生成随机数的部分,而 rand 则指定了生成数组的形状。
2:初始化w和b是初始化每一个特征的w和一个公用的b,所以我们需要特征的数量,也就是dim
3: 每一个特征的w–>使用数组一一对应
4: 一个公用的b–>直接赋值0
很简单,直接上代码:
def initialize_zeros(dim):
#dim是每一个图片的特征数量,也就是X.shape[0],也就是12288
#每一个特征都需要一个权重w,而所有特征通常共享一个偏置项b。
#为了创建可以和训练集X计算的权重矩阵w:
#dim:传入的数据集的第一个向量坐标,X.shape[0]
#一些博客里面会这样写
#w=np.zeros(shape=(dim,1))
#这样做的目的是将所有的值用0填充,但是这样也许会导致一个“对称性”问题
#当你这样初始化权重并使用它们在神经网络中时,每一层的所有神经元都会有相同的输出。
#因此,当你进行反向传播时,所有神经元都会收到相同的梯度。这将导致所有的权重都更新为相同的值。无论网络有多少神经元,它们都会表现得像一个神经元,这极大地限制了网络的容量和表达能力。
#所以我们使用随机
#每一个特征都需要一个w,
#1. 在 NumPy 中,np.random.rand() 函数用于生成一个给定形状的数组,这里特征数组的形状是(dim,1)
#2. 数组的值,其中的每个元素都是从 [0, 1) 区间的均匀分布中随机抽取的。
w=0.01*np.random.rand(dim,1)#乘以0.01是为了确保初始化的权重值很小。
b=0
#使用断言来检测是正确
assert(w.shape==(dim,1))
assert(isinstance(b,float) or isinstance(b,int))
return (w,b)
初始化参数的函数已经构建好了,现在就可以执行“前向”和“后向”传播步骤来学习参数。
补充:链式法则与导数
链式法则是微积分中一个非常重要的原则,用于计算复合函数的导数。
在深度学习和神经网络中,链式法则是反向传播算法的基础,它使得我们能够有效地计算损失函数相对于各个权重的梯度。
个人看法:为什么用导数?因为要用链式法则; 为什么用链式法则?因为要从后向前反向传播。
链式法则的定义
假设: 你有两个函数 f 和 g,并且这两个函数组合在一起形成了一个复合函数 h
即 h(x) = f(g(x))。
链式法则告诉我们,如果你想要计算复合函数 h 相对于 x 的导数,你可以将 f 相对于 g 的导数乘以 g 相对于 x 的导数。用数学术语来表示就是:
d
h
d
x
=
d
f
d
g
⋅
d
g
d
x
\frac{dh}{dx} = \frac{df}{dg} \cdot \frac{dg}{dx}
dxdh=dgdf⋅dxdg
在深度学习中的应用
在深度学习中,一个神经网络可以被看作是由多个函数组成的复合函数,其中每个函数代表网络中的一个层。
当我们训练神经网络时,我们的目标是最小化损失函数,这是网络输出和真实值之间差异的量化。
为了实现这一点,我们需要根据损失函数相对于网络中每个权重的梯度来调整这些权重。这就是链式法则发挥作用的地方:
1.在前向传播过程中: 数据通过网络的每一层进行传递,每一层都应用其特定的运算(如线性变换后接激活函数)。
2.在反向传播过程中: 我们从输出层开始计算损失函数相对于每一层输出的梯度(导数)。
然后,使用链式法则,我们可以一层层向后计算,直到达到输入层,从而得到损失函数相对于所有权重的梯度。
3.逐层更新权重: 使用这些梯度,我们可以调整网络中每一层的权重,以减少总损失。
假设: 考虑一个简单的神经网络层,其输出 y 由输入 x、权重 w 和偏置 b 通过函数 y = f(wx + b) 计算得出。在这里,f 可能是一个激活函数,如ReLU或Sigmoid。如果我们想要计算损失 L 相对于 w 的梯度,我们就会使用链式法则:
d
L
d
w
=
d
L
d
y
⋅
d
y
d
w
\frac{dL}{dw} = \frac{dL}{dy} \cdot \frac{dy}{dw}
dwdL=dydL⋅dwdy
其中, d L d y \frac{dL}{dy} dydL 是损失相对于层输出的梯度,而 d y d w \frac{dy}{dw} dwdy 是层输出相对于权重的梯度。通过链式法则,我们可以将这两个梯度相乘,从而得到我们需要的梯度 d L d w \frac{dL}{dw} dwdL。这种方法可以用来对网络中的所有权重进行类似的计算。
补充:向量化计算
简单来说,就是使用.np函数库里面的函数代替For循环计算
.np.dot() 是 NumPy 库中的一个函数,用于进行向量乘法或矩阵乘法。
所谓“向量化”,指的是编程中一种特定的处理方式,它可以同时对数组或矩阵中的多个元素执行相同的操作,而无需显式编写循环语句。这种处理方式可以显著提高计算效率,特别是在涉及大型数据集时。
1,当使用 np.dot() 对两个一维数组进行操作时: 它执行的是两个向量的点积。
例如,如果有两个向量 a = [a1, a2, …, an] 和 b = [b1, b2, …, bn],那么它们的点积计算为 a1b1 + a2b2 + … + an*bn。
2,当用于二维数组(或更高维度)时: np.dot() 执行的是矩阵乘法,这也是一种向量化的操作。
在矩阵乘法中,第一个矩阵的行与第二个矩阵的列对应相乘,然后将结果求和,形成新的矩阵。这种操作方式大大提高了计算效率,尤其是在处理大规模数据时。
五、构建传播函数
神经网络或者深度学习模型单次的训练过程有四个阶段:
- 前向传播:给当前数据 x i x^i xi,根据算法(当前我们用的是sigmoid函数)输出一个结果 y ^ i \hat y^i y^i
- 计算机损失:得到前向传播的预测 y ^ i \hat y^i y^i以后,我们会评估“预测与我们给定的标签 y i y^i yi之间的差异。这个差异(通常称为“损失”或“误差”)
- 后向传播:基于前面计算的损失,模型会计算每个参数的梯度,以知道如何更好地更新参数来提高预测。这个步骤就是告诉模型:“为了减少预测误差,你应该这样调整你的参数w和b。”
- 更新参数: 在知道了如何更新参数之后,实际更新参数。
到目前为之,我们已经完成了前两步的基本实现和理论概括。我将会在这个章节将它们进行组合,实现完整的前向传播和后向传播。
不过在此之前,我们还需要引入一个东西:损失函数
5.1 损失函数
补充:下面这些废话当个乐看看就行,核心知识点:
这个函数的作用为,将
y
^
i
\hat{y}^i
y^i和
y
i
{y}^i
yi输入到损失函数中:
1:如果两个数差异很小,即都是趋近于0或者趋近于1, 那么得到的值(损失)趋近于0;
2:如果两个数差异很大,即一个趋近于0而另外一个趋近于1,那么得到的值(损失)趋近于无穷;
详细解析:
很久很久以前,在一座威严耸立的山上。一群数学家在给一群哲学家分完筷子以后,闲的无聊。这个时候,突然有人想到了一个问题:
有没有什么办法可以让标签 ( y i {y^i} yi) 为 1 的 x i {x^i} xi 的预测值 ( y ^ i \hat{y}^i y^i) 趋近于 1?
有没有什么办法可以让标签 ( y i {y^i} yi) 为 0 的 x i {x^i} xi 的预测值 ( y ^ i \hat{y}^i y^i) 趋近于 0?
这个时候,有一个拿到 两!根!筷!子! 的哲学家说,简单啊,你让
可以让标签 (
y
i
{y^i}
yi) 为 1 的
x
i
{x^i}
xi 的预测值 (
y
^
i
\hat{y}^i
y^i) 不趋近于 0
可以让标签 (
y
i
{y^i}
yi) 为 0 的
x
i
{x^i}
xi 的预测值 (
y
^
i
\hat{y}^i
y^i) 不趋近于 1
在把这个哲学家祭天以后,一个数学家仔细琢磨这句话,说:“不如这样吧,我们可以想一个公式,在公式里面同时输入 y i {y^i} yi和 y ^ i \hat{y}^i y^i。如果这两个的值很相近呢,就让这个公式的输出的值小一点。如果不相近呢,就让它的输出大一点。”
“那我们用 对数(log) 吧!” 另一个数学家说道。
“既然不相近,我们假设这个公式的输出为 L o s s Loss Loss吧!代表 “损失”:
如果输入的
y
i
{y^i}
yi为 1 ,我就让
L
o
s
s
=
−
log
(
y
^
(
i
)
)
Loss= -\log(\hat{y}^{(i)})
Loss=−log(y^(i)), 这样如果
y
^
i
\hat{y}^i
y^i接近 0 时,S会特别大,反之会特别小。
如果输入的
y
i
{y^i}
yi为 0, 我就让
L
o
s
s
=
−
log
(
1
−
y
^
(
i
)
)
Loss = -\log(1 - \hat{y}^{(i)})
Loss=−log(1−y^(i)), 这样如果
y
^
i
\hat{y}^i
y^i接近 1 时,S会特别大,反之会特别小。”
“那我们把它们结合一下吧,成为一个公式。同时让这两个公式添加两个非0即1的相反的乘数。虽然是一个公式,但是同时只有一半可以用。“
“我看就用 y i {y^i} yi 和 1 − y i 1-{y^i} 1−yi 吧,这两个不是标签么?非0即1”
“太棒了!让我再来添加一个帅气的符号吧!把它变成:
L
o
s
s
=
L
(
y
,
y
^
)
=
−
[
y
log
(
y
^
)
+
(
1
−
y
)
log
(
1
−
y
^
)
]
Loss=L(y, \hat{y}) = -[y \log(\hat{y}) + (1 - y) \log(1 - \hat{y})]
Loss=L(y,y^)=−[ylog(y^)+(1−y)log(1−y^)]”
“太帅了!!!,我们给它取一个名字吧!同时找一个帅气的翻译者,把它翻译词让人 望!而!生!畏! 的中文吧!”
“那就叫:
二元交叉熵损失函数(Binary Cross-Entropy Loss,也称为log loss)
吧!”
“既然有处理单个数据的函数了,那么我们再改善一下吧,让它可以处理多个数据吧!”
“这好办呀!假设有 M M M个数据,我们把每一个单一的数据结果加起来,然后再除以 M M M不就好了吗?”
“既然结果依赖于 y ^ ( i ) \hat{y}^{(i)} y^(i)和 y ( i ) {y}^{(i)} y(i),同时 y ( i ) {y}^{(i)} y(i)和 x ( i ) {x}^{(i)} x(i)是给定的不能修改,那么可以说结果决度定于 y ^ ( i ) \hat{y}^{(i)} y^(i)”
“ y ^ ( i ) \hat{y}^{(i)} y^(i)不是来源于 y ^ ( i ) = 1 1 + e − ( w T ⋅ x ( i ) + b ) \hat{y}^(i) = \frac{1}{1 + e^{-( w^T \cdot x^{(i)} + b)}} y^(i)=1+e−(wT⋅x(i)+b)1吗?而且刚刚不是有个高大威猛帅气的男生说 逻辑回归的目标,就是找到合适的 w w w和 b b b 吗?那我们干脆直接用 w w w和 b b b作表示吧,那不就是…”
J ( w , b ) = 1 m ∑ i = 1 m L ( y ( i ) , y ^ ( i ) ) J(w, b) = \frac{1}{m} \sum_{i=1}^{m} \text{L}(y^{(i)}, \hat{y}^{(i)}) J(w,b)=m1i=1∑mL(y(i),y^(i))
这,就是损失函数(Cost Function / Loss Function)
在深度学习中,我们需要找合适的 w w w和 b b b,尽可能的缩小 J ( w , b ) J(w,b) J(w,b)
5.2 前向传播
通过我们现在的知识,可以构建前向传播了。
核心知识点:
1: m=X.shape[1],提取样本的总个数
2: A=sigmoid(np.dot(w.T,X)+b) 中的得到的A就是预测值
前向传播(Forward Propagation): 是神经网络中的一个过程,其中输入数据从输入层流经网络的每一层,直到最后生成输出。在这个过程中,每一层的神经元接收上一层的输出(对于第一层,接收输入数据),并通过加权和以及激活函数产生该层的输出。这些输出随后被传递到下一层,直至达到输出层。
前向传播的目的是基于当前的参数(权重和偏置)和输入数据来计算网络的输出。当得到网络的输出之后,我们可以将它与真实的目标或标签值进行比较,从而计算损失。
代码:
#前向传播:计算损失
def propagate(w,b,X,Y):
#传入的参数:
# w:权重向量,维度为[X.shape[0],1]
#每一个元素的值随机 参见初始化函数
#w的第一个维度应该等于X.shape[0],为什么?因为w.T也就是[1,X.shape[0]]要X进行点乘 参见线性回归函数
# b:偏差,一个常数
# X:输入的矩阵,当前为 (12288, 209)
# Y:标签矩阵 ,当前为(1,209)
#返回的参数
#cost:当前一轮训练完成后,计算得到的损失值的平均,单个的点相较于决策边界的成本的总和的平均
m=X.shape[1] #X的第二个参数,也就是样本的总个数
#Z=w.T*X+b #线性函数
A=sigmoid(np.dot(w.T,X)+b) #sigmoid函数(将线性函数集成了)
#此时这里A是一个矩阵,里面的内容是模型的预测值
#使用向量化以后的组合
cost=(-1/m)*np.sum(Y*np.log(A) + (1-Y)*(np.log(1-A)))
#注意,因为计算机的时候参与了Y矩阵,所以这个时候cost里面有一个下标为1,对于Y(1,209)来说这个1是确保Y是一个矩阵,但是对于cost,这个1是无用的,我们需要移除
cost=np.squeeze(cost)
return cost
5.3 后向传播
现在我们已经知道了“损失”,我们便可以通过“损失”的大小来反向的调整 w w w和 b b b,使得 z = w T ⋅ x + b z = w^T \cdot x + b z=wT⋅x+b 画出来的决策边界可以尽可能的拟合所有的点。
怎么做呢?
使用梯度下降
5.3.1 梯度下降算法
核心知识点:
0:如果要运行一次梯度下降,dz是关键核心
1:梯度下降的方向是斜率(导数)的负方向。
2:梯度下降法的目标通常是优化至斜率(在一维情况下)或梯度(在多维情况下)等于0的点。在这些点上,函数没有进一步增长或减少的方向,这通常意味着找到了局部极小值。在一维情况下,这对应于函数曲线上的切线斜率为零的点;在多维情况下,则是梯度的每个分量都为零的点
3:对于w的更新是对于每一个特征的w进行更新,所以得到的dw仍然是一个数组
4:读与b的更新,因为是公用的,直接求和平均计算得到常数
梯度下降算法它的公式为:
对于
w
w
w的更新:
1:求损失函数
J
J
J关于权重
w
w
w的偏导数
∂
J
∂
w
=
1
m
X
(
Y
^
−
Y
)
T
\frac{\partial J}{\partial w} = \frac{1}{m} X (\hat{Y} - Y)^T
∂w∂J=m1X(Y^−Y)T
2:新的
w
w
w等于当前
w
−
a
w-a
w−a倍的损失函数
J
J
J关于权重
w
w
w的偏导数
w
=
w
−
α
∂
J
∂
w
w = w - \alpha \frac{\partial J}{\partial w}
w=w−α∂w∂J
对于
b
b
b的更新:
1:求损失函数
J
J
J关于权重
b
b
b的偏导数
∂
J
∂
b
=
1
m
∑
i
=
1
m
(
y
^
(
i
)
−
y
(
i
)
)
\frac{\partial J}{\partial b} = \frac{1}{m} \sum_{i=1}^{m} (\hat{y}^{(i)} - y^{(i)})
∂b∂J=m1i=1∑m(y^(i)−y(i))
2:新的
b
b
b等于当前
b
−
a
b-a
b−a倍的损失函数
J
J
J关于权重
b
b
b的偏导数
b = b − α ∂ J ∂ b b = b - \alpha \frac{\partial J}{\partial b} b=b−α∂b∂J
这些公式,有兴趣的小伙伴可以自行推导一下,方法很简单,使用链式法则。
为什么要求导呢?为什么求导数可以反推呢?
别问,用就行。管它意大利的还是东北山里的,能响就好炮。
5.4 前向传播和后向传播完整代码
结合前向传播的片段,我们现在可以写出本章完整的代码
注意:由于我们还需要将学习率参与到运算中,所以这个函数返回的是dw和db的需要更新多少,并不是真的已经更新完的值。
def propagate(w,b,X,Y):
#传入的参数:
# w:权重向量,维度为[X.shape[0],1]
#每一个元素的值随机 参见初始化函数
#w的第一个维度应该等于X.shape[0],为什么?因为w.T也就是[1,X.shape[0]]要X进行点乘 参见线性回归函数
# b:偏差,一个常数
# X:输入的矩阵,当前为 (12288, 209)
# Y:标签矩阵 ,当前为(1,209)
#返回的参数
#cost:当前一轮训练完成后,计算得到的损失值的平均,单个的点相较于那条线的成本的总和的平均
#dw:后向传播以后,w需要改变多少
#db:后向传播以后,b需要改变多少
m=X.shape[1] #X的第二个参数,也就是样本的总个数
#前向传播:也就是执行一次逻辑回归和损失计算,也就是执行那三个函数
#Z=w.T*X+b #线性函数
A=sigmoid(np.dot(w.T,X)+b) #sigmoid函数(将线性函数集成了)
#此时这里A是一个矩阵,里面的内容是模型的预测值
#使用向量化以后的组合
cost=(-1/m)*np.sum(Y*np.log(A) + (1-Y)*(np.log(1-A)))
#注意,因为计算机的时候参与了Y矩阵,所以这个时候cost里面有一个下标为1,对于Y(1,209)来说这个1是确保Y是一个矩阵,但是对于cost,这个1是无用的,我们需要移除
cost=np.squeeze(cost)
#反向传播:(计算w和b需要改变多少)
#为了计算w和b,我们需要使用梯度下降算法,它的公式是:
# w= w - 学习率 * 损失函数对于w的导数
dz=A-Y
dw = (1/m) * np.dot(X,dz.T)
db = (1/m) * np.sum(dz)
#确保数据是否正确
assert(dw.shape == w.shape)
assert(db.dtype == float)#断言会失败,导致程序抛出一个 AssertionError 异常。
assert(cost.shape == ())
#创建一个字典,把dw和db保存起来。
grads={
"dw":dw,
"db":db
}
return (grads,cost)
5.4.1 :关于dz的说明
dz实际上代表的是损失函数对激活函数输出 A 的导数,在sigmoid函数中
d
z
=
(
Y
^
−
Y
)
=
(
y
^
(
i
)
−
y
(
i
)
)
dz = (\hat{Y} - Y)= (\hat{y}^{(i)} - y^{(i)})
dz=(Y^−Y)=(y^(i)−y(i))
对于单个的z和b
d
w
=
x
⋅
d
z
dw=x ⋅ dz
dw=x⋅dz
d z = d b dz=db dz=db
六、模型使用
现在,我们已经有了实现所有功能的代码,我们使用一些聚合函数将它们逐步聚合。
这样做的好处有很多,最主要的是如果代码出现问题,我们不用盯着一大块代码段查找bug…同时,作为学习者,分块写代码可以方便我们以后查阅和复习
6.1 运行梯度下降更新w和b
#通过最最小化成本函数J来学习w和b
def optimize (w,b,X,Y,num_itertions,learning_rate,print_cost = False):
# 此函数通过运行梯度下降算法来优化w和b
# 参数:
# w - 权重,大小不等的数组(num_px * num_px * 3,1)
# b - 偏差,一个标量
# X - 维度为(num_px * num_px * 3,训练数据的数量)的数组。
# Y - 真正的“标签”矢量(如果非猫则为0,如果是猫则为1),矩阵维度为(1,训练数据的数量)
# num_iterations - 优化循环的迭代次数
# learning_rate - 梯度下降更新规则的学习率,就是那个阿尔法
# print_cost - 每100步打印一次损失值
# 返回:
# params - 包含权重w和偏差b的字典
# grads - 包含权重和偏差相对于成本函数的梯度的字典
# 成本 - 优化期间计算的所有成本列表,将用于绘制学习曲线。
# 提示:
# 我们需要写下两个步骤并遍历它们:
# 1)计算当前参数的成本和梯度,使用propagate()。
# 2)使用w和b的梯度下降法则更新参数。
costs=[]
for i in range (num_itertions):
grads, cost =propagate(w,b,X,Y)
dw = grads["dw"]
db = grads["db"]
#公式
w = w-learning_rate *dw
b = b-learning_rate *db
#记录成本
if i %100 ==0:
costs.append(cost)
#打印成本数据
if (print_cost) and (i % 100 ==0):
print("迭代的次数: %i , 误差值: %f" % (i,cost))
#创建字典保存w和b
params={"w":w,"b":b}
grads={"dw":dw,"db":db}
return (params,grads,costs)
# print("====================测试optimize====================")
# #([[1],[2]])一维的数组,有两个元素[1]和[2]
# w,b,X,Y=np.array([[1],[2]]), 2 , np.array([[1,2],[3,4]]), np.array([[1,0]])
# params,grads,costs=optimize(w,b,X,Y,num_itertions=100,learning_rate = 0.009,print_cost = False)
# print ("w = " + str(params["w"]))
# print ("b = " + str(params["b"]))
# print ("dw = " + str(grads["dw"]))
# print ("db = " + str(grads["db"]))
6.2 模型使用:构建预测函数(计算数据转化的值)
现在我们得到了训练好的w和b,也就是训练好的模型。
我们可以使用w和b来预测数据集X的所生成的标签,预测标签是0还是1。
我们要实现预测函数。计算预测有两个步骤:
1.计算
Y
=
A
=
σ
(
w
T
X
+
b
)
Y ^ = A = σ ( w^TX + b )
Y=A=σ(wTX+b)
2.选定sigmoid函数的阈值,将
a
a
a变为0(如果激活值<=0.5)或者1(如果激活值>0.5),
a
a
a 表示神经元的激活值,
A
A
A 是sigmoid激活函数
σ
σ
σ 的输出矩阵。
def predict(w,b,X):
#使用学习逻辑回归参数logistic(w,b)预测标签是0还是1,
# 参数:
# w - 权重,大小不等的数组(num_px * num_px * 3,1)
# b - 偏差,一个标量
# X - 维度为(num_px * num_px * 3,训练数据的数量)的数组。
# 返回:
# Y_prediction - 包含X中所有图片的所有预测【0 | 1】的一个numpy数组(向量)
m=X.shape[1] #图片的数量
Y_prediction =np.zeros((1,m)) #创建都是0的矩阵(1行m列)
w=w.reshape(X.shape[0],1) #将w转为一个图片参数的累乘,维度为1
#预测猫在图片中出现的概率
A=sigmoid(np.dot(w.T,X)+b)
for i in range(A.shape[1]):
#将概率a[0,1]转化为实际预测的p[0.i]
Y_prediction[0,i] = 1 if A[0,i] >0.5 else 0
#使用断言
assert(Y_prediction.shape==(1,m))
return Y_prediction
# print("====================测试predict====================")
# w, b, X, Y = np.array([[1], [2]]), 2, np.array([[1,2], [3,4]]), np.array([[1, 0]])
# print("predictions = " + str(predict(w, b, X)))
6.3 聚合
就目前而言,我们基本上把所有的东西都做完了,现在我们要把这些函数统统整合到一个model()函数中,届时只需要调用一个model()就基本上完成所有的事了。
def model(X_train , Y_train , X_test , Y_test , num_iterations = 2000 , learning_rate = 0.5 , print_cost = False):
w , b = initialize_zeros(X_train.shape[0])
parameters , grads , costs = optimize(w , b , X_train , Y_train,num_iterations , learning_rate , print_cost)
#从字典“参数”中检索参数w和b
w , b = parameters["w"] , parameters["b"]
#预测测试/训练集的例子
Y_prediction_test = predict(w , b, X_test)
Y_prediction_train = predict(w , b, X_train)
#打印训练后的准确性
print("训练集准确性:" , format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100) ,"%")
print("测试集准确性:" , format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100) ,"%")
d = {
"costs" : costs,
"Y_prediction_test" : Y_prediction_test,
"Y_prediciton_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations" : num_iterations }
return d
# print("====================测试model====================")
# #这里加载的是真实的数据,请参见上面的代码部分。
# d = model(train_set_x, train_set_y_orig, test_set_x, test_set_y_orig, num_iterations = 2000, learning_rate = 0.005, print_cost = True)
# #绘制图
# costs = np.squeeze(d['costs'])
# plt.plot(costs)
# plt.ylabel('cost')
# plt.xlabel('iterations (per hundreds)')
# plt.title("Learning rate =" + str(d["learning_rate"]))
# plt.show()
七、完整代码
以下是完整代码:
#所谓模型:就是一个(组)参数适合的公式
#所谓学习:就是找那个合适的参数!
#导入序列化必要函数
import numpy as np
#导入生成图片要的包
import matplotlib.pyplot as plt
# 是在 Python 中导入 matplotlib 库的 pyplot 模块并为其指定一个简称 plt 的语句。matplotlib 是一个非常流行的 Python 数据可视化库,它提供了一套全面的绘图工具来制作各种静态、动态或交互式的图形。
# pyplot 是 matplotlib 的一个子模块,通常被认为是该库的核心。它提供了一个类似于 MATLAB 的绘图界面,使得创建图形变得非常简单。
#导入针对数据格式的包
import h5py
# import h5py 是 Python 中引入 h5py 库的命令。
# h5py 是一个 Python 库,它提供了一种高效的方式来读取和写入 HDF5 格式的文件。
# HDF5(Hierarchical Data Format version 5)是一个流行的数据存储格式,常用于大型数据集,如科学计算或深度学习中的训练数据。
# HDF5 文件可以包含大量的数据集并支持高效的并行IO操作,它提供了一种结构化的方式来存储数据,其中数据可以被组织为不同的组和数据集。
#从lr_utils文件(或者称为模块,每一个py文件就是一个模块)导入函数
from lr_utils import load_dataset
#load_dataset函数是对训练集合和测试集合的预处理,并且已经封装好了,提取就可以
train_set_x_orig,train_set_y_orig,test_set_x_roig,test_set_y_orig,classes=load_dataset()#classes是一个字段,就是将 0 表示非猫("non-cat")图片,1 表示猫("cat")文字说明
#查看一下两个数据集有多少数据,几个维度
"""
print(train_set_x_orig.shape) #(209, 64, 64, 3) 训练集:209行的后面那三个维度的矩阵
print(train_set_y_orig.shape) #(1, 209) 训练集标签:1行的209个数据 训练数据集是由209个 64*64的3色域图片组成
print(test_set_x_roig.shape) #(50, 64, 64, 3) 测试集50行的后面那三个维度的矩阵
print(test_set_y_orig.shape) #(1, 50) 测试集标签:1行的50个数据
"""
#降低维度,改变数组的位置(转置)
#匹配标签数据集和训练数据集的维度,将高维度的转化为低纬度
#转置是为了方便计算,把209放到后面,和标签一样
#公式:将A(a,b,c,d)转化为A(b*c*d,a)
#X=X.reshape(X.shape[0],-1).T
#X=X.reshape() 重塑数组的维度
#(A,B)二维数组
#X.shape[0] 第一个维度不变
#-1在reshape方法中有一个特殊的意义。它表示该维度的大小应当被自动推断,以保证总元素数不变。
#为了计算-1应该被替代的值,numpy会使用以下方法:
#总元素数 / 已知的其他维度的大小 = 未知维度的大小
#在A(m,n,o)中,原始数组的总元素数是m * n * o。已知的其他维度的大小是m。所以,-1会被计算为(m * n * o) / m = n * o。
#因此,形状为(m, n, o)的三维数组会被重新形状为(m, n*o)的二维数组。
#.T 二维数组前后交换
# #测试
# a=np.random.rand(5,2,3)#创建[5,2,3]维度的数组,用随机数填满
# print(a.shape) #(5, 2, 3)
# print((a.reshape(a.shape[0],-1).T).shape) #[6,5]
#print(train_set_x_orig.shape) #(209, 64, 64, 3)
train_set_x_flatten=train_set_x_orig.reshape(train_set_x_orig.shape[0],-1).T #(12288, 209)
# print(train_set_x_flatten.shape)
# print(test_set_x_roig.shape)#(50, 64, 64, 3)
test_set_x_flatten=test_set_x_roig.reshape(test_set_x_roig.shape[0],-1).T #(12288, 50)
# print(test_set_x_flatten.shape)
#将数据集中化和标准化,因为都是图片数据,所以可以除以255,将每个数据控制到[0,1]之间
train_set_x=train_set_x_flatten/255
# print(train_set_x.shape)#数据的维度还是没变(12288, 209)
test_set_x=test_set_x_flatten/255
#数据处理的部分完成了,接下来就是构建神经网络
#我们要处理的是二分类问题,而“逻辑回归”是处理二分问题的一个算法
#逻辑回归,实际上是找到一个决策边界,然后根据样本点相对于这个边界的位置来分类,对于线性逻辑回归,这个决策边界是一条直线(在二维空间中)或一个超平面(在更高的维度中),这取决于特征的数量。
#逻辑回归函数=线性回归函数+sigmoid函数,所以我们需要两个函数
#1.线性回归函数:Z = z^(i) = w.T ∙ x^(i)+b
# x^(i):第i个样本的特征向量
# w:权重向量,表示当前x^(i)的权重比(权重用于决定决策边界怎么画)
# w.T是w的转置,我们为了计算w与x的“点乘”,要求w的行向量 == x的列向量
# 如果你的 w 向量本来就是一个行向量,并且它的长度(列数)与 x 向量的长度(行数)相同,不需要再进行转置,但是,权重向量和特征向量通常都被定义为列向量,这是一种约束。
#b: 这是偏置项,它是一个常数
#z^(i):第i个样本的线性输出。输入一个x^(i),在当前函数中,得到一个z(i)
#2.sigmoid函数:a=1/1+e^(-Z) //其中的Z是线性回归函数
#是一种激活函数
#输出范围:[0,1]
#拟合,实际上是指尽量减少误分类的数量,总有一些点无法分类,而我们需要找到可以尽可能的满足多点的决策边界,所以我们需要是最小化逻辑回归的损失函数(通常是对数损失函数或交叉熵损失函数)
#所以我们还需要一个损失函数参数:
#L(a^(i),y^(i) = -y^(i)*log(a^(i)) - (1-y^(i))*log(1-a^(i))
#最后,我们需要一个对于所有数据的损失求和的函数:假设所有数据一共有m个
# J=1/m * m∑(i=1)* L(a^(i),y^(i))
#构建sigmoid函数
def sigmoid(z):
a=1/(1+np.exp(-z))
return a
#初始化函数
#主要用于构建w和b,之前看到的方法是创建一个(dim,1)维度的0向量
# w=np.zeros(shape=(dim,1))
#但是这样也许会导致一个“对称性”问题
#当你这样初始化权重并使用它们在神经网络中时,每一层的所有神经元都会有相同的输出。
#因此,当你进行反向传播时,所有神经元都会收到相同的梯度。这将导致所有的权重都更新为相同的值。无论网络有多少神经元,它们都会表现得像一个神经元,这极大地限制了网络的容量和表达能力。
def initialize_zeros(dim):
#dim:传入的数据集的第一个向量坐标,X.shape[0]
#w=np.zeros(shape=(dim,1))
w=0.01*np.random.rand(dim,1)#乘以0.01是为了确保初始化的权重值很小。
b=0
#使用断言来检测是正确
assert(w.shape==(dim,1))
assert(isinstance(b,float) or isinstance(b,int))
return (w,b)
#构建逻辑回归的前向传播和后向传播
#神经网络或者深度学习模型单次的训练过程有四个阶段:
#1.前向传播:给当前数据x^(i),根据算法(当前我们用的是sigmoid函数)输出一个结果[sigmoid的范围是[0,1]]
#2.计算机损失:得到前向传播的数据(预测)以后,我们会评估“预测与我们给定的标签y^(i)”之间的差异。这个差异(通常称为“损失”或“误差”)
#3.后向传播:基于前面计算的损失,模型会计算每个参数的梯度,以知道如何更好地更新参数来提高预测。这个步骤就是告诉模型:“为了减少预测误差,你应该这样调整你的参数w和b。”
#4.更新参数: 在知道了如何更新参数之后,实际更新参数。
#构建实现上述功能的函数(渐变函数)
def propagate(w,b,X,Y):
#传入的参数:
# w:权重向量,维度为[X.shape[0],1]
#每一个元素的值随机 参见初始化函数
#w的第一个维度应该等于X.shape[0],为什么?因为w.T也就是[1,X.shape[0]]要X进行点乘 参见线性回归函数
# b:偏差,一个常数
# X:输入的矩阵,当前为 (12288, 209)
# Y:标签矩阵 ,当前为(1,209)
#返回的参数
#cost:当前一轮训练完成后,计算得到的损失值的平均,单个的点相较于那条线的成本的总和的平均
#dw:后向传播以后,w需要改变多少
#db:后向传播以后,b需要改变多少
m=X.shape[1] #X的第二个参数,也就是样本的总个数
#前向传播:也就是执行一次逻辑回归和损失计算,也就是执行那三个函数
#Z=w.T*X+b #线性函数
A=sigmoid(np.dot(w.T,X)+b) #sigmoid函数(将线性函数集成了)
#此时这里A是一个矩阵,里面的内容是模型的预测值
#使用向量化以后的组合
cost=(-1/m)*np.sum(Y*np.log(A) + (1-Y)*(np.log(1-A)))
#注意,因为计算机的时候参与了Y矩阵,所以这个时候cost里面有一个下标为1,对于Y(1,209)来说这个1是确保Y是一个矩阵,但是对于cost,这个1是无用的,我们需要移除
cost=np.squeeze(cost)
#反向传播:(计算w和b需要改变多少)
#为了计算w和b,我们需要使用梯度下降算法,它的公式是:
# w= w - 学习率 * 损失函数对于w的导数
dz=A-Y
dw = (1/m) * np.dot(X,dz.T)
db = (1/m) * np.sum(dz)
#确保数据是否正确
assert(dw.shape == w.shape)
assert(db.dtype == float)#断言会失败,导致程序抛出一个 AssertionError 异常。
assert(cost.shape == ())
#创建一个字典,把dw和db保存起来。
grads={
"dw":dw,
"db":db
}
return (grads,cost)
#通过最最小化成本函数J来学习w和b
def optimize (w,b,X,Y,num_itertions,learning_rate,print_cost = False):
# 此函数通过运行梯度下降算法来优化w和b
# 参数:
# w - 权重,大小不等的数组(num_px * num_px * 3,1)
# b - 偏差,一个标量
# X - 维度为(num_px * num_px * 3,训练数据的数量)的数组。
# Y - 真正的“标签”矢量(如果非猫则为0,如果是猫则为1),矩阵维度为(1,训练数据的数量)
# num_iterations - 优化循环的迭代次数
# learning_rate - 梯度下降更新规则的学习率,就是那个阿尔法
# print_cost - 每100步打印一次损失值
# 返回:
# params - 包含权重w和偏差b的字典
# grads - 包含权重和偏差相对于成本函数的梯度的字典
# 成本 - 优化期间计算的所有成本列表,将用于绘制学习曲线。
# 提示:
# 我们需要写下两个步骤并遍历它们:
# 1)计算当前参数的成本和梯度,使用propagate()。
# 2)使用w和b的梯度下降法则更新参数。
costs=[]
for i in range (num_itertions):
grads, cost =propagate(w,b,X,Y)
dw = grads["dw"]
db = grads["db"]
#公式
w = w-learning_rate *dw
b = b-learning_rate *db
#记录成本
if i %100 ==0:
costs.append(cost)
#打印成本数据
if (print_cost) and (i % 100 ==0):
print("迭代的次数: %i , 误差值: %f" % (i,cost))
#创建字典保存w和b
params={"w":w,"b":b}
grads={"dw":dw,"db":db}
return (params,grads,costs)
# print("====================测试optimize====================")
# #([[1],[2]])一维的数组,有两个元素[1]和[2]
# w,b,X,Y=np.array([[1],[2]]), 2 , np.array([[1,2],[3,4]]), np.array([[1,0]])
# params,grads,costs=optimize(w,b,X,Y,num_itertions=100,learning_rate = 0.009,print_cost = False)
# print ("w = " + str(params["w"]))
# print ("b = " + str(params["b"]))
# print ("dw = " + str(grads["dw"]))
# print ("db = " + str(grads["db"]))
def predict(w,b,X):
#使用学习逻辑回归参数logistic(w,b)预测标签是0还是1,
# 参数:
# w - 权重,大小不等的数组(num_px * num_px * 3,1)
# b - 偏差,一个标量
# X - 维度为(num_px * num_px * 3,训练数据的数量)的数组。
# 返回:
# Y_prediction - 包含X中所有图片的所有预测【0 | 1】的一个numpy数组(向量)
m=X.shape[1] #图片的数量
Y_prediction =np.zeros((1,m)) #创建都是0的矩阵(1行m列)
w=w.reshape(X.shape[0],1) #将w转为一个图片参数的累乘,维度为1
#预测猫在图片中出现的概率
A=sigmoid(np.dot(w.T,X)+b)
for i in range(A.shape[1]):
#将概率a[0,1]转化为实际预测的p[0.i]
Y_prediction[0,i] = 1 if A[0,i] >0.5 else 0
#使用断言
assert(Y_prediction.shape==(1,m))
return Y_prediction
# def model(X_train,Y_train,X_test,Y_test, num_iterations=2000,learning_rate =0.005, print_cost=False):
# #参数:
# # X_train -numpy的数组,维度为(num_px*num_px*3,m_train)的训练集
# # Y_train -numpy的数组,维度为(1,m_train)(标签)(矢量)的训练集合
# # X_test -numpy的数组,维度为(num_px*num_px*3,m_test)的测试集
# # Y_test -numpy的数组,维度为(1,m_test)(标签)(矢量)的测试集合
# # num_iterations - 用于优化参数的迭代次数
# # learning_rate --学习率
# # print_cost - 设置为true以每100次迭代打印成本
# #返回
# #d -包含模型信息的字典
# w,b=initialize_zeros(X_train.shape[0]) #初始化w和b,根据训练集合的第一个参数(那一堆东西)
# parameters,grads,costs=optimize(w,b,X_train,Y_train,num_iterations,learning_rate,print_cost)
# #从字典“参数”中检索参数w和b
# w,b = parameters["w"],parameters["b"]
# #预测测试/训练集的例子
# Y_prediction_test =predict(w,b,X_test)
# Y_prediction_train=predict(w,b,X_train)
# #打印
# #用于计算数据的平均值:np.mean()
# print("训练集的准确度:",format(100-np.mean(np.abs(Y_prediction_train-Y_train))*100),"%")
# print("测试集的准确度:",format(100-np.mean(np.abs(Y_prediction_test-Y_test))*100),"%")
# d = {
# "costs" : costs,
# "Y_prediction_test" : Y_prediction_test,
# "Y_prediciton_train" : Y_prediction_train,
# "w" : w,
# "b" : b,
# "learning_rate" : learning_rate,
# "num_iterations" : num_iterations }
# return d
# print("====================测试model====================")
# d1=model(train_set_x,train_set_y_orig,test_set_x,test_set_y_orig,num_iterations =2000,learning_rate =0.01,print_cost=True)
# d2=model(train_set_x,train_set_y_orig,test_set_x,test_set_y_orig,num_iterations =2000,learning_rate =0.001,print_cost=True)
# d3=model(train_set_x,train_set_y_orig,test_set_x,test_set_y_orig,num_iterations =2000,learning_rate =0.0001,print_cost=True)
# #绘图
# costs1=np.squeeze(d1['costs'])
# plt.plot(costs1)
# costs2=np.squeeze(d2['costs'])
# plt.plot(costs2)
# costs3=np.squeeze(d3['costs'])
# plt.plot(costs3)
# plt.ylabel('cost')
# plt.xlabel(('iterations (per hundreds)'))
# plt.title("Learning rate =" + str(d1["learning_rate"])+str(d2["learning_rate"])+str(d3["learning_rate"]))
# plt.show()
def model(X_train , Y_train , X_test , Y_test , num_iterations = 2000 , learning_rate = 0.5 , print_cost = False):
w , b = initialize_zeros(X_train.shape[0])
parameters , grads , costs = optimize(w , b , X_train , Y_train,num_iterations , learning_rate , print_cost)
#从字典“参数”中检索参数w和b
w , b = parameters["w"] , parameters["b"]
#预测测试/训练集的例子
Y_prediction_test = predict(w , b, X_test)
Y_prediction_train = predict(w , b, X_train)
#打印训练后的准确性
print("训练集准确性:" , format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100) ,"%")
print("测试集准确性:" , format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100) ,"%")
d = {
"costs" : costs,
"Y_prediction_test" : Y_prediction_test,
"Y_prediciton_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations" : num_iterations }
return d
print("====================测试model====================")
#这里加载的是真实的数据,请参见上面的代码部分。
d = model(train_set_x, train_set_y_orig, test_set_x, test_set_y_orig, num_iterations = 2000, learning_rate = 0.005, print_cost = True)
#绘制图
costs = np.squeeze(d['costs'])
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()
最后,我们得到了这样的结果和图片
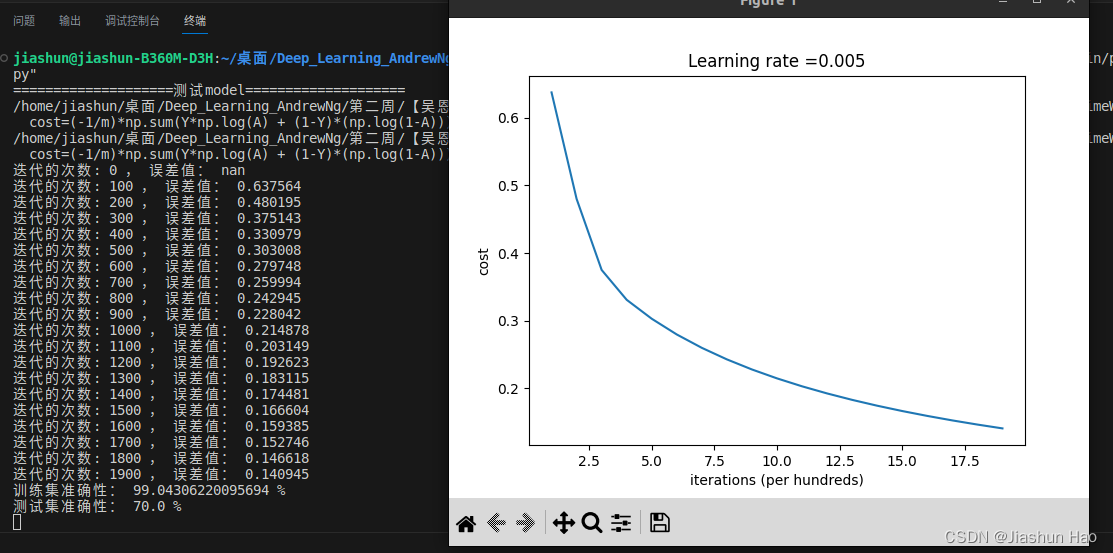
再玩一下?好的!
让我们最后修改一下学习率,看看会有什么样的变化
如果你也想玩,替换最后的打印语句即可:
print("====================测试model====================")
d1=model(train_set_x,train_set_y_orig,test_set_x,test_set_y_orig,num_iterations =2000,learning_rate =0.01,print_cost=True)
d2=model(train_set_x,train_set_y_orig,test_set_x,test_set_y_orig,num_iterations =2000,learning_rate =0.001,print_cost=True)
d3=model(train_set_x,train_set_y_orig,test_set_x,test_set_y_orig,num_iterations =2000,learning_rate =0.0001,print_cost=True)
#绘图
costs1=np.squeeze(d1['costs'])
plt.plot(costs1)
costs2=np.squeeze(d2['costs'])
plt.plot(costs2)
costs3=np.squeeze(d3['costs'])
plt.plot(costs3)
plt.ylabel('cost')
plt.xlabel(('iterations (per hundreds)'))
plt.title("Learning rate1 =" + str(d1["learning_rate"])+'\n'+"Learning rate2 =" + str(d2["learning_rate"])+'\n'+"Learning rate2 =" + str(d2["learning_rate"]))
plt.show()
得到的结果是这样滴!
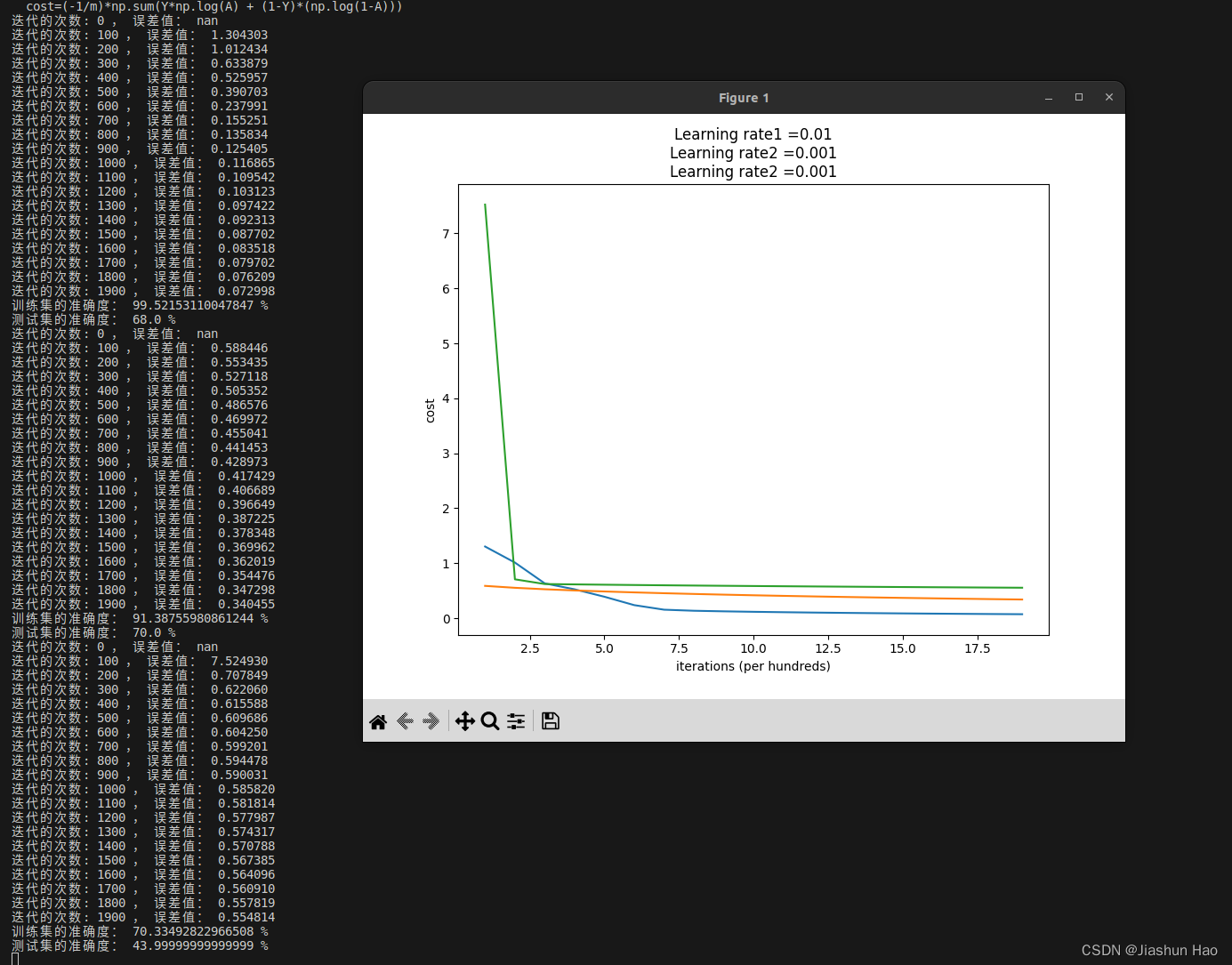
为什么呢?
学习率会有影响
我知道,为什么会这样呢?
你猜?
写在后面的话
这应该是我注册CSDN以来写的最畅快的一片博客。
对于标题:《打开深度学习的锁》,其实有很多自负,我甚至连那扇门都没有看到,但我依然感觉的到,我解开了一些东西,这种感觉很舒服,也很自豪。
好似小学课堂上,我第一次解开方程组,老师奖励的那块糖。我早已记不清糖的味道,但它打开了我喜欢数学的门,这种感觉是甜甜的。这道题,打开我对于深度学习的那把锁,也解开了束缚在心中的焦虑,以此,畅快,可得一夜的安眠。
退一步想,很久没有写博客了,为什么不写呢?原因很多:没时间、没心气、没东西.
曾经这是我学习的一种的方式,本人比较笨,也比较懒,对于一个知识点,往往需要很长的周期才可以掌握,因为需要一个可以随时查阅的网络笔记,彼时CSDN刚刚兴起,便注册,也依然希望沉淀一点东西,然后写下来。保留这份难得沉下心,这个为了一个目标的渴望与完成时的激动。也在未来的某个时段,作为引子,以供以后的自己检索回忆。
看自己是增是减。
我写过很多没用的东西,但就是这些东西记录了当年那个小小的自己,自顾自的向前走,时不时跌到、颓废、崩溃、抑郁、焦虑、然后起身、振作、自我调节、继续行走。如今回到看,那个少年也走出了一条窄窄的路,只是运气占了大多数。
那个孩子,仍然在以自己的方式——迎接自己渴望的欢呼,承受自己唾弃的鄙夷,走下去。
郝佳顺
2023年9月9日
于韩国庆北大学
最后一次修改:2023/12/04(在每一个章节后面添加“核心知识点”方便理解)





















 615
615

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








