打开深度学习的锁：（3）进阶知识补充

零、深度学习的技巧

1.偏差和方差解决技巧

1 先要解决偏差问题，当偏差解决以后再考虑方差问题。

2 当进行方差操作以后，一定要再次测试新的策略的会不会再次导致偏差问题, 也就是当解决了过拟合操作以后，一定要再次测试一下会不会欠拟合

减小偏差

• 使用更复杂的模型
• 增加模型参数
• 减少正则化强度

减小方差

• 使用更多的训练数据
• 简化模型
• 增加正则化强度（如L2正则化）
• 使用集成方法（如bagging和boosting）

2.深度网络层数

先设计逻辑回归，然后一点点增加隐藏层的数量。

一、深度学习的核心

在深度学习中，模型的核心组成可以包括以下几个方面：

1. 参数（Weights and Biases）

• 权重 ( w )：连接神经元之间的参数，用于调整输入特征的重要性。在深度神经网络中，每一个特征有自己的权重。宏观到每一层，不同的层都有自己的权重矩阵。
• 偏置 ( b )：每个神经元都有一个偏置，用于调整模型的输出，使其更灵活地拟合数据。

2. 网络架构（Network Architecture）

• 层数（Layers）：深度神经网络由多层神经元组成，包括输入层、隐藏层和输出层，但是在计算层数的时候不包括输入层。

  在计算的时候，一般使用 $L$ 或者 $l$ 来所在表示层的位置。

• 神经元数（Neurons）：每一层中的神经元数，也决定了该层的复杂度。

  用 $n$来表示神经元的数量，第 $l$ 层的神经元表示为$n^{[l]}$

• 线性函数（Linear Functions）：提供基本的线性函数计算。

  公式为 $z=Wx+b$，第 $l$ 层的线性函数为$z^{[l]}=W^{[l]}{a}^{[l-1]}+b^{[l]}$，$a^{[l-1]}$为前一层的激活值，对于第一层来说$a^{[l-1]}$是输入层。

  $a_i^{[l]}$表示第$l$ 层的第 $i$ 个神经元的激活值

• 激活函数（Activation Functions） 转换线性函数到非线性，如ReLU、sigmoid、tanh等，用于引入非线性，使模型能够学习复杂的模式。

  公式为 $a^{[l]}=g(z^{[l]})$，激活函数统一用 $g$ 表示，激活值为 $a$，但是具体的算法则不一样。

2.1. 激活函数和其导数

Sigmoid 函数：

$$\sigma (x)=\frac{1}{1+e^{-x}}$$
导数公式：
$$\frac{d\sigma (z^{[l]})}{d{z}^{[l]}}=a^{[l]}(1-a^{[l]})$$

ReLU 函数：

$$\text{ReLU}(x)=\max (0,x)$$
导数公式：
$$\frac{d\text{ReLU}(z^{[l]})}{d{z}^{[l]}}=\{\begin{array}{ll}1& \text{if }{z}^{[l]}>0\\ 0& \text{if }{z}^{[l]}\le 0\end{array}$$

Tanh 函数：

$$\tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$
导数公式：
$$\frac{d\tanh (z^{[l]})}{d{z}^{[l]}}=1-(a^{[l]}{)}^2$$
$${\tanh }^{\prime }(x)=1-{\tanh }^2(x)$$

3. 损失函数（Loss Function）

• 用于衡量模型预测值与真实值之间的差距。常见的损失函数有均方误差（MSE）、交叉熵损失（Cross-Entropy Loss）等。

4. 优化算法（Optimization Algorithm）

• 用于更新模型参数以最小化损失函数。常见的优化算法有随机梯度下降（SGD）、Adam、RMSprop等。

5. 正则化（Regularization）

• 防止过拟合的技术，如L1/L2正则化、Dropout等。

6. 学习率（Learning Rate）

• 控制每次参数更新的步长大小，是优化过程中非常关键的超参数。

二、训练集、开发集、测试集

1：训练集（Training Set）：60-80%

训练集的作用是为了学习数据的特征和模式，使模型能够对输入数据进行准确的预测。
主要的任务是获得学习到的 “模型”，也就是 $W$ 和 $b$ 的值。

2：开发集（或验证集，Development Set/Validation Set）：10-20%

在使用训练集获得了模型，即确定了$W$ 和 $b$ 的值以后使用开发集来测试==超参数==调优，例如学习率、正则化系数等。

2：测试集（Test Set）：10-20%

检测最终的模型的性能，用于最终评估模型性能的数据集。

三：Bias（偏差）和Variance（方差）

Bias（偏差）

偏差是指模型预测值与真实值之间的差异。
高偏差表示模型在训练数据和测试数据上的预测都较差，即模型欠拟合（underfitting）。偏差高的模型通常过于简单，无法捕捉数据中的复杂模式。

特征：

• 模型过于简单
• 无法很好地拟合训练数据
• 训练误差和测试误差都很高
  

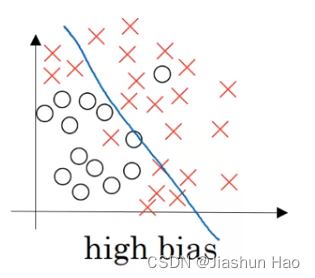
Variance（方差）

方差是指模型对训练数据中随机噪声的敏感程度。
高方差表示模型在训练数据上表现很好，但在测试数据上表现较差，即模型过拟合（overfitting）。方差高的模型通常过于复杂，只记住训练数据中的噪声，但无法泛化到新的数据。

特征：

• 模型过于复杂
• 在训练数据上表现很好，但在测试数据上表现较差
• 训练误差低，测试误差高

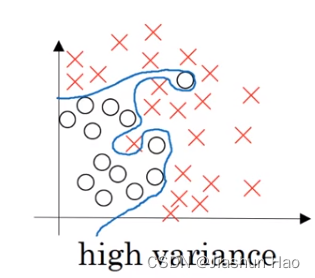
Bias-Variance Tradeoff（偏差-方差权衡）

偏差和方差之间存在权衡关系，即在降低偏差的同时可能会增加方差，反之亦然。理想情况下，模型应当在偏差和方差之间找到一个平衡点，以确保其在训练数据和测试数据上都能有较好的表现。

1. 高偏差、低方差：

   • 简单的线性模型
   • 训练误差和测试误差都较高

2. 低偏差、高方差：

   • 复杂的神经网络模型
   • 训练误差低，测试误差高

3. 适中偏差、适中方差：

   • 适度复杂的模型，如带有正则化的神经网络
   • 训练误差和测试误差都在合理范围内

解决方法

先要解决偏差问题，当偏差解决以后再考虑方差问题。

当进行方差操作以后，一定要再次测试新的策略的会不会再次导致偏差问题

减小偏差

• 使用更复杂的模型
• 增加模型参数
• 减少正则化强度

减小方差

• 使用更多的训练数据
• 简化模型
• 增加正则化强度（如L2正则化）
• 使用集成方法（如bagging和boosting）

四：正则化（Regularization）

正则化就是利用一些手段，在模型训练解决解决模型过拟合、提高范化能力等问题。

不同的方法作用的阶段不同。

不过这之前需要明白一个概念：重要特征和最高权重

1. 重要特征和最高权重

PS:以下全为个人抽象理解，未来有极大概率修改这段话，切勿照本宣科。

在深度学习中，重要特征指的是“对预测影响较大”的特征值。

假设样本X有俩个特征：x1为0.9，x2为0.1

如果此时标签Y是1,那么x1就是重要特征，如果标签为0,那么x2就是重要特征。

虽然最后的关于特征的表示，是特征*权重，但是权重的值一般都比较小，类似0.01

即使一开始给非重要特征设置了高权重，在一次次优化中（类似梯度下降）非重要特征的权重也会变低，重要特征的权重会变高。

所以，从结果导向来看：重要特征就是权重高的特征，非重要特征就是权重低的特征

2. L1正则化（Lasso正则化）：作用于损失函数和权重

$$J(w,b)=\frac{1}{m}\sum _{i=1}^{m}L({\hat{y}}^i,y^i)+\frac{\lambda }{m}\sum _{\ell =1}^L\Vert {\omega }^{[\ell ]}\Vert$$

$$\text{d}{\omega }^{[\ell ]}=\frac{dJ}{d{\omega }^{[\ell ]}}+\frac{\lambda }{m}\text{sign}({\omega }^{[\ell ]})$$

解析：简单来说Lasso正则化就是在原有的损失函数上增加了一个 $\lambda$ 倍的权重的方差，这样会导致如下的结果：

1：由于增加的内容基于权重的值，对于大权重的特征来说，损失会增大，所以下一次更新的时候权重会被减少很多。
2：对于小权重的特征来说，损失也会增大，但也没有那么大，所以下一次更新的时候权重会减少但是没有很多。

抽象举例，假设：大权重为100,小权重为1

这样操作以后，下一次更新也许大权重会变为 1 , 减少了99，也许小权重会变为 0.1，减少了 0.9。

虽然大权重变少了很多，但是还是比小权重高，所以对于模型来说，大权重的特征的重要性还是比小权重的特征的重要性要高。

为什么降低特征的权重可以减少过拟合呢？

因为可以减少对个别特征的过度依赖。泛化能力不足往往与模型对个别特征的过度依赖有关

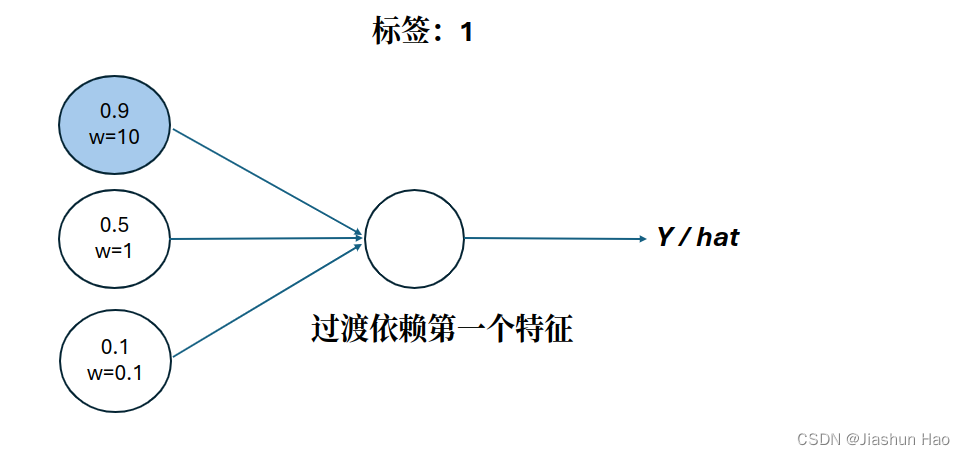
此外，降低权重还有另外作用，减小非重要特征的影响力–权重被趋近于0。减小网络复杂度

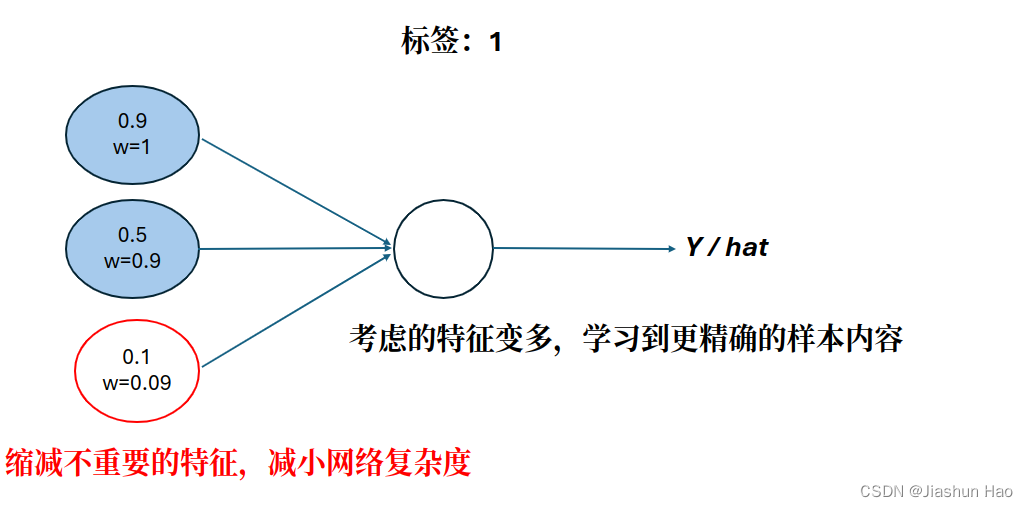
对第一层来说，减小的是输入的特征的权重，优化的是输入样本的特征。

但是对于深度网络的其它层来说，减小是上一层的输出的权重，优化的则是上一层神经网络

L1正则化前：
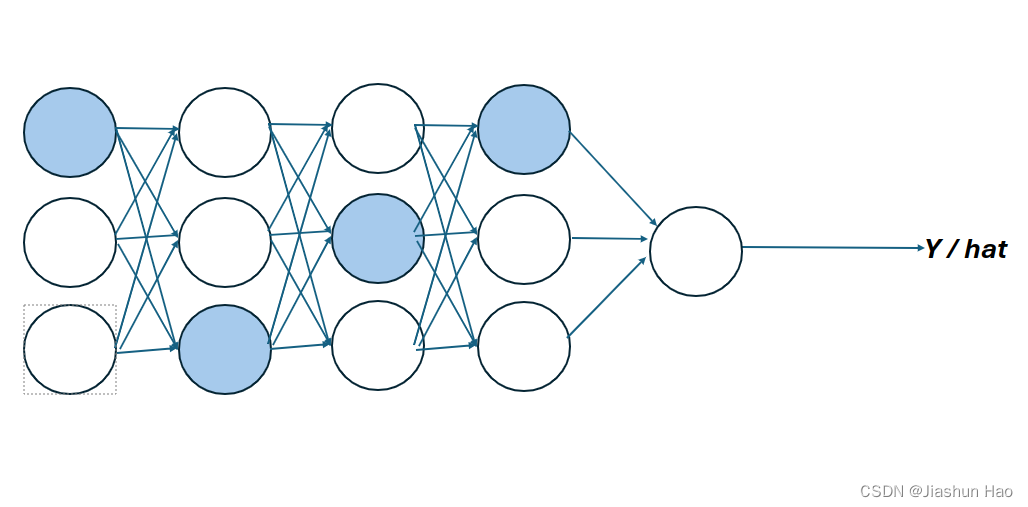L1正则化后：

3. L2正则化（Ridge正则化）：作用于损失函数和权重

$$J(w,b)=\frac{1}{m}\sum _{i=1}^{m}L({\hat{y}}^i,y^i)+\frac{\lambda }{2m}\sum _{j=1}^n{w}_j^2$$

$$\text{d}{\omega }^{[\ell ]}=\frac{dJ}{d{\omega }^{[\ell ]}}+\frac{\lambda }{m}{\omega }^{[\ell ]}$$
实现代码：

#np.square 数组里面每一个值都平方
regularization =(1/m)*(lambd/2)*(np.sum(np.square(W1))+np.sum(np.square(W2))+np.sum(np.square(W3)))

原理于L1类似，差异如下：

区别

• L1正则化会导致模型参数中许多值变为零，从而产生稀疏解。这是因为L1正则化倾向于在优化过程中沿参数的坐标轴将其推向零，这也有助于特征选择。
• L2正则化倾向于将参数值均匀地减小，而不是将它们推向零。这可以防止任何一个参数对模型结果产生过大影响，从而减轻模型过拟合的问题。

对异常值的敏感度

• L1正则化对于异常值较不敏感，因为它倾向于选择某些特征而忽略其他特征，这使得模型更加简单且稳健。
• L2正则化由于平方项的存在，对异常值较敏感，特别是当异常值的平方会对损失函数造成很大影响时。

解的唯一性

• L1正则化可能会因为稀疏性而不产生唯一解，特别是当一些特征高度相关时。
• L2正则化通常会产生唯一解，因为添加的惩罚项 $\lambda {\sum }_{j=1}^n{w}_j^2$ 确保了损失函数是严格凸的。

应用场景

• L1正则化常用于特征选择和处理高维数据的场景，尤其是当一些特征是多余的或者相关性很高时。
• L2正则化更适用于防止模型复杂度过高，需要处理模型中所有特征大体上都是重要的情况。

选择L1还是L2正则化通常取决于具体问题的需求和数据的特性。

例如，如果你需要一个简化的模型来解释模型是如何做出决策的（特征选择），L1可能是更好的选择。

如果你需要确保模型的所有参数都小一些，从而增强模型的泛化能力，那么L2可能是更合适的选择。同时L2也是最常用的正则化手段。

在实践中，也可以同时使用L1和L2正则化，这种组合被称为弹性网（Elastic Net）正则化。

4. Dropout正则化：作用于激活值

Dropout正则化不能用于测试阶段！！Dropout正则化不能用于测试阶段！！

相较于L1和L2利用损失函数来间接的弱化一些不重要的神经元。

Dropout 的核心思想更直接，就是在每次训练迭代中，随机将一些神经元的激活值 $a$ 设置为零，每次训练设置的神经元都不同。

Dropout 丢弃的不是神经元，丢弃的是当前个别神经元对于样本的预测，

或者说丢弃的是当前层某一个神经元对于原始输入样本的预测，每次训练迭代中丢的都不一样。

这个过程涉及到公式不明朗（在我看来是这样…）所以在此直接记录完成的代码。

# A的维度（当前神经元个数，样本的个数）
# A3：存放第三层的5个神经元对于最开始输入的10个样本的预测
A3 = np.random.randn(5, 10)

# 开始
# 1.设置 keep_prob 为 0.8 (即有 0.2 的概率舍弃)
keep_prob = 0.8 #概率为1-keep_prob

# 2.设计一个和A3形状一样的随机数矩阵
D3 = np.random.rand(a3.shape[0], a3.shape[1]) # 这里用的是rand，在[0,1) 之间取值
D3 = D3 < keep_prob #用True 和 False 随机填充 D3

# 3.利用随机矩阵的True 和 False随机丢弃 A3中的值
A3 = A3 * D3 #True == 1 / False == 0

# 4.扩大A3的值
A3 = A3/keep_prob #因为有（1-keep_prob）也就是20%，的值被舍弃了，所以扩大20%。
# A3= A3 /（8/10）
# A3= A3 *（10/8） 

#......
# 5.更新导数，从后向前
dA3 = dA3 * D3               
dA3 = dA3 / keep_prob 

dA2 = dA2 * D2               
dA2 = dA2 / keep_prob 
#.....

其实我还是有点不理解第4步，不过先这样记着吧。

此外， Dropout正则化的设置比较灵活，对于重要的层，比如最后的输出层，我们也可以不用 Dropout，把 keep_prob 设置为1。

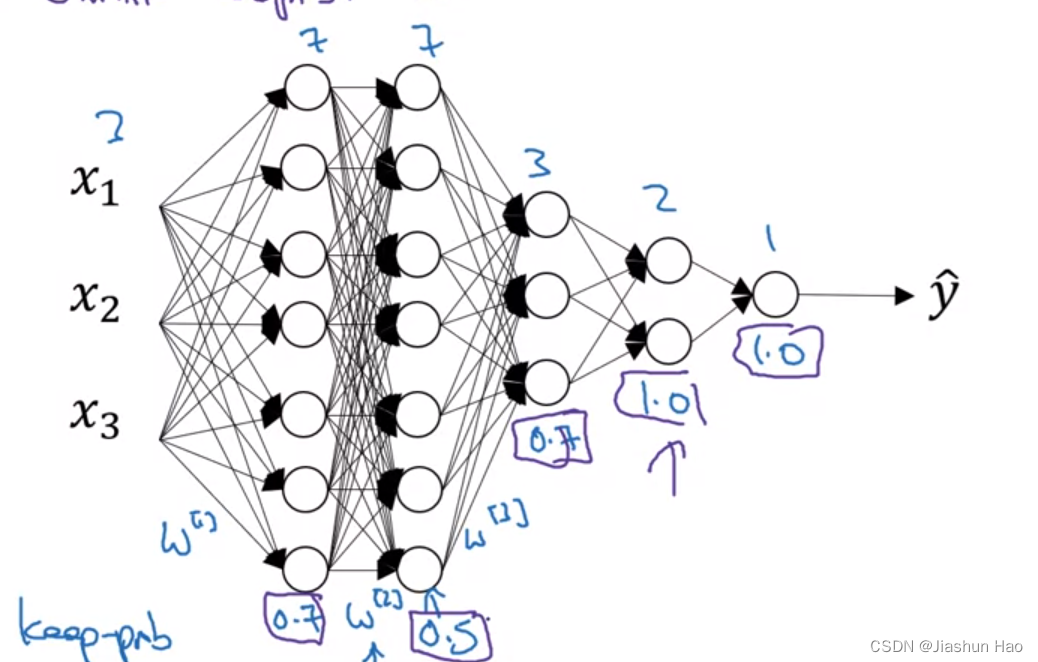
5. 其它正则化：

1.歪门邪道–数据扩增（Data Augmentation）

简单来说就是修改当前有的数据集为新数据。

举例数据集数据为图片，那么就可以水平反转图片、裁切图片、图片轻微扭曲。

2.早停法（Early Stopping）：基于验证集

简单来说，就是在测试寻找超参数（迭代次数、学习率等）的时候，找一个对于验证集来说损失最低的$W$和$b$, 即使这个$W$和$b$不是对于训练集的损失最低。

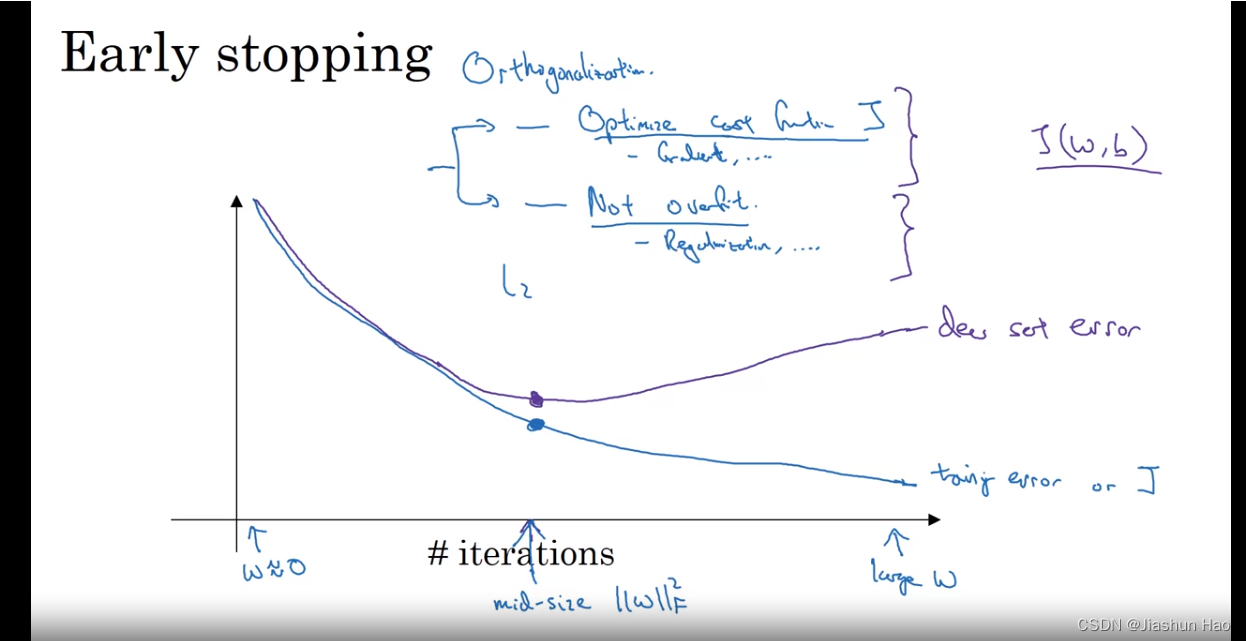
五、设置优化问

除了正则化以外，一些对于设置的优化方式，也可以帮助建立更好的模型，主要有以下几点。

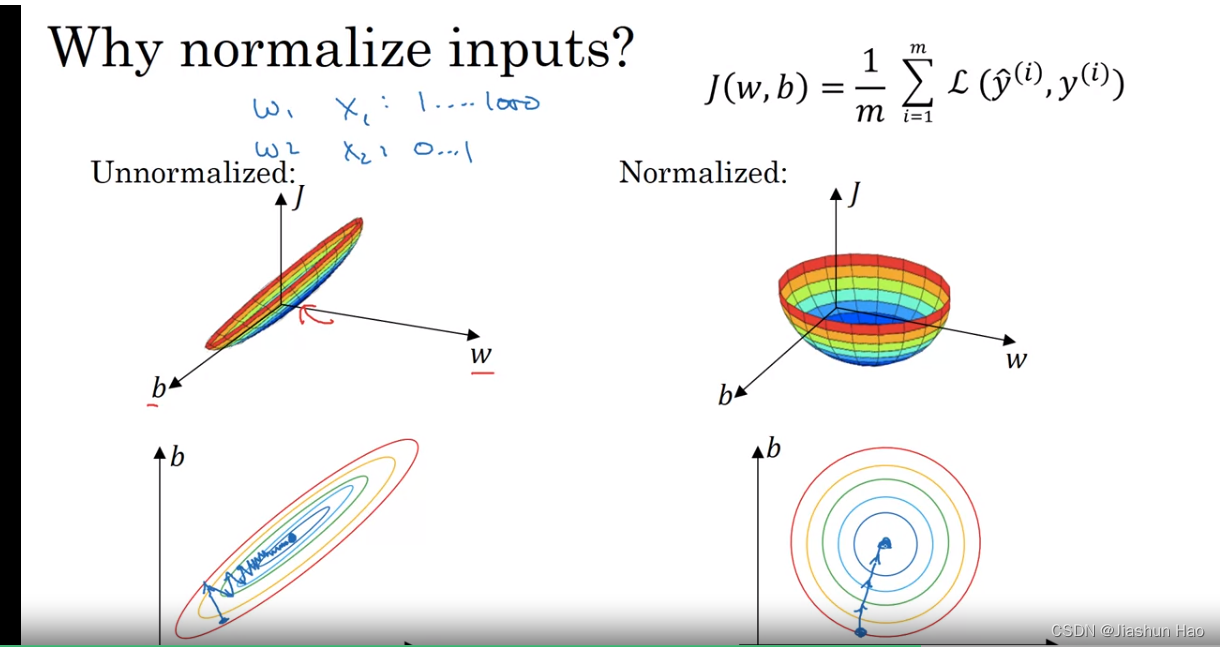
1. 输入：Normalizing化

目的：可以将数据聚合到以0为原点，的方差标准化为 1。

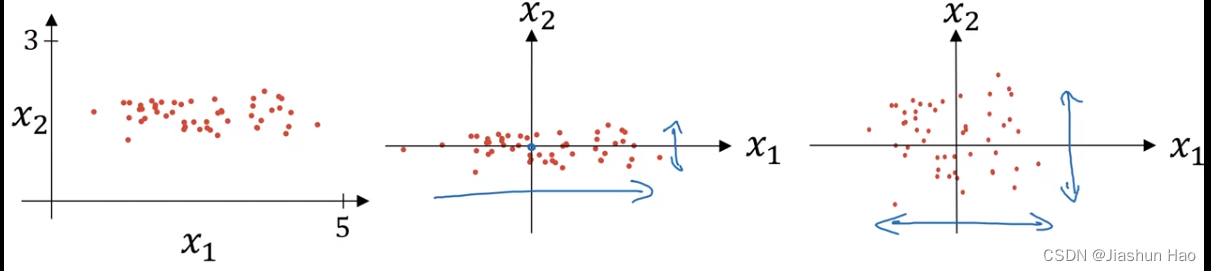
公式：

第一步，获得输入的均值：
$$\mu =\frac{1}{m}\sum _{i=1}^m{x}^{(i)}$$
第二步，计算方差：
$${\sigma }^2=\frac{1}{m}\sum _{i=1}^m(x^{(i)}-\mu {)}^2$$
于是标准差：
$$\sigma =\sqrt{\frac{1}{m}\sum _{i=1}^m(x^{(i)}-\mu {)}^2}$$

第三步，最终的标准化数据：
$$x^{\prime }=\frac{x-\mu }{\sigma }$$

通过输入Normalizing化，可以让特征分布的更均匀，损失函数图形更像一个碗，更容易梯度下降。

2. 防止梯度爆炸/梯度消失

防止梯度爆炸/梯度消失，主要是因为对于深层的神经网络，如果用统一的方式初始化 W 矩阵，W的初始值都相同。

在后续涉及到 W 乘法操作中可能会导致 W 过大或者过小，继而导致 Z 过大或者过小。

所以我们需要优化W的初始化，即对不同的层用不同的W初始化函数

对于不同的激活函数，初始化的方法也不一样

1.对于ReLU作为激活函数: He

	WL=np.random.rand(shape) * np.sqrt( 2.0 / 前一层的神经元个数) # np.sqrt( 2 / n[l-1])
	# W的形状为（n[l], n[l-1]），n[l]为当前神经元个数； n[l-1]为前一层的神经元个数

2.对于Tanh\sigmoid 作为激活函数: Xavier

	WL=np.random.rand(shape) * np.sqrt( 1.0 / 前一层的神经元个数) # np.sqrt( 2 / n[l-1])
	# W的形状为（n[l], n[l-1]），n[l]为当前神经元个数； n[l-1]为前一层的神经元个数

也有第二个版本

	WL=np.random.rand(shape) * np.sqrt( 2.0 / (前一层的神经元个数)+(当前层的神经元个数)) # np.sqrt( 2 / n[l-1])
	# W的形状为（n[l], n[l-1]），n[l]为当前神经元个数； n[l-1]为前一层的神经元个数

3. 梯度检查（Gradient Checking）

当模型出现一些问题的时候，我们需要逐一排查，其中一个很重要的部分是对 “梯度下降算法”和“反向传播”的检查，要进行梯度检查，必须要考虑下面这三点：

1. 只有在debug的时候，代码调式的时候才可以使用。训练测试的时候不要使用。
2. 考虑代码中是否用了正则化
3. 不能与 dropout 一起用

1. 中心差分公式

梯度检查的核心来源于中心差分公式：
$$f^{\prime }(x)\approx \frac{f(x+h)-f(x-h)}{2h}$$
$$函数f（x）在x的点导数\approx \frac{f(x+一个微小的偏量)-f(x-一个微小的偏量)}{2\ast 一个微小的偏量}$$

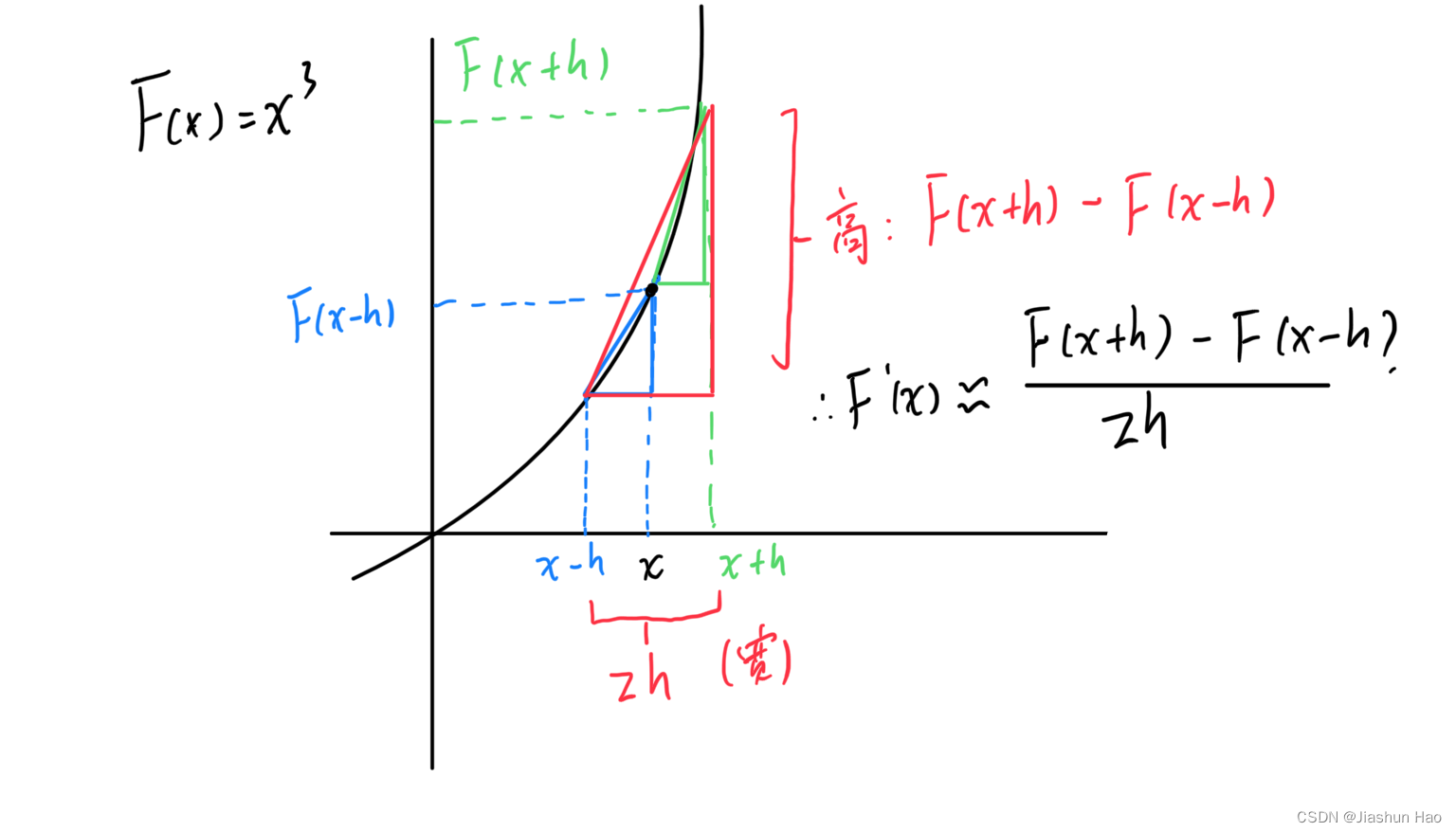
不过，这个方法有一个必要的前提条件，

那就是 $h$, 这个移动的标量必须是一个极小值，类似$10^{-7}.所得到的误差一般为h^2$

2. 梯度检查

1. 首先，将所有 $L$ 层网络中的每一个 $W$ 和 $b$ 聚合为一个单位

# θ ={w1,b1,w2,b2....wl,bl}
theta=np.concatenate([w1.flatten(),b1 , w2.flatten(),b2 , w3.flatten(),b3 , .....)}

2. 然后，我们计算近似导数 dθ 的值

for i = L:
 dθ = (J(θ1,θ2,θ3.....θi+h,...,θL)-J(θ1,θ2,θ3.....θi-h,...,θL)) / 2h

3. 计算似导数 dθ 集与实际导集合的相对公差（relative error）

$$\text{relative error}=\frac{\Vert d\theta -{\text{grad}}_{\text{analytic}}\Vert }{\Vert d\theta \Vert +\Vert {\text{grad}}_{\text{analytic}}\Vert }$$

这个移动的标量必须是一个极小值，类似 $10^{-7}$

如果 $h$ 是 $10^{-7}$ ，那么relative error的值应该在 $10^{-5}$ 到 $10^{-9}$ 之间，否则为异常。

六、小批量梯度下降（Mini-batch gradient descent）

梯度下降的方法有两种，一种是之前一直使用的利用全部的训练数据进行梯度下降，专业名词叫批量梯度下降，这样做有以下的特点：

1. 使用整个训练集计算梯度并更新参数。
2. 优点：收敛方向稳定。
3. 缺点：计算代价高，特别是对于大数据集。

如果涉及到数据集很大，计算成本太高，所有有人提出了随机梯度下降，简单来说就是使用一个样本来进行梯度下降，这样可以很快速的更新梯度

1. 每次只使用一个样本计算梯度并更新参数。

2. 优点：计算代价低，可以更快地进行迭代。

3. 缺点：梯度更新的方向波动较大，导致收敛不稳定。不会收敛，在一个低点摆动。

结合二者的优点，提出了小批量梯度下降，即使用1 < M < 训练样本总数 的 数据去进行梯度下降，综合收敛方向稳定 和 计算代价低，可以更快地进行迭代 的优点

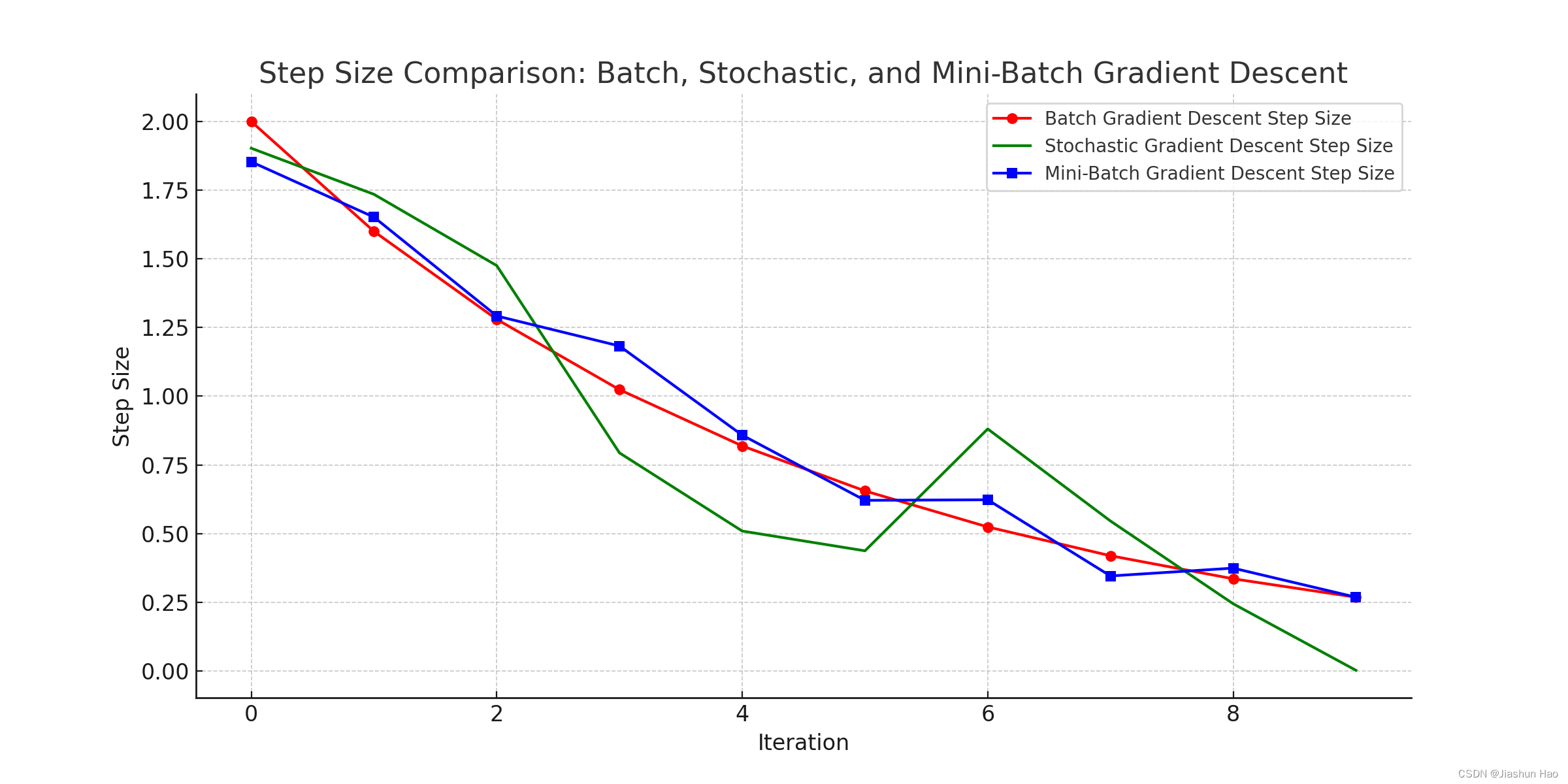
使用小批量梯度下降，建议遵守下面的规范：

1. 当数据量 >= 2000 时，再使用小批量梯度下降。数据量太小没意义
2. 每一个小批量集合里面的样本个数，遵循 $2^x$ ，建议使用64、128、256、512…
3. 确保所有的小批量集合可以被CPU和GPU所容纳。
4. 小批量集合的大小也是一个超参数！！ (可调)
5. 每一个小批量集合，用$X^{【i】}$表示

1. 伪代码

L = len(parameters) // 2 # number of layers in the neural networks

for l in range(1, L + 1): #神经网络层数
	#前向传播 : X[t]
	Z[1]=W[1]X[t]+b[1]
	A[1]=g[1](Z[1])
	....
	A[L]==g[L](Z[L])#L是层数
	
	# 计算损失函数：使用第t个小批量数据的预测值 Y_hat[t] 和真实值 Y[t]
	Cost J[t] = (1 / 小批量集规模) * np.sum(损失函数(Y[t], Y_hat[t])) + 正则化项
	
	#反向传播：计算J[t]的梯度，用X[t]和Y[t]
	dW[L], db[L] = 计算梯度(第L层, A[L], Y[t])
    ...
    dW[1], db[1] = 计算梯度(第1层, A[1], Y[t])
    
    #更新
	W[L] ：= W[L]- alpha * dW[L]
	b[L] ：= b[L]- alpha * db[L]
	....
	W[1] ：= W[1]- alpha * dW[1]
	b[1] ：= b[1]- alpha * db[1]

2. 实现代码

X #input data, of shape (input size, number of examples)
Y #true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
m = X.shape[1]  #样本总数
mini_batch_size = 64 #小批量数据的大小
np.random.seed(seed)#随机种子，用于确保每次生成的随机小批量数据都是相同的。

#1：打乱数据
permutation = list(np.random.permutation(m))	#生成随机的顺序
shuffled_X = X[:, permutation]					#按照随机的顺序重新排列每一行
shuffled_Y = Y[:, permutation].reshape((1, m))

#2：分割数据
mini_batch_size= 10 # 每一个子集容纳的数据的大小

# 批次,要划分的子集的个数
# num_complete_minibatches=100 
num_complete_minibatches = math.floor(m / mini_batch_size) #总数除以每一个子集容纳的数据，然后向上取整数

for k in range(0, num_complete_minibatches):
	#使用切片截断取数
	mini_batch_X = shuffled_X[:, k * mini_batch_size : (k + 1) * mini_batch_size]
    mini_batch_Y = shuffled_Y[:, k * mini_batch_size : (k + 1) * mini_batch_size]
	
	#组合这些到一个列表，方便以后使用
	mini_batch = (mini_batch_X, mini_batch_Y)
    mini_batches.append(mini_batch)
    
#如果总数和划分的批次不是倍数关系，即存在没有被完整划分的剩余部分    
if m % mini_batch_size != 0:
	#num_complete_minibatches * mini_batch_size 等于整数划分的终点数
    mini_batch_X = shuffled_X[:, num_complete_minibatches * mini_batch_size : m] #从终点数到m的所有数被分为一个集合
    mini_batch_Y = shuffled_Y[:, num_complete_minibatches * mini_batch_size : m]
	
	#追加到列表
	mini_batch = (mini_batch_X, mini_batch_Y)
    mini_batches.append(mini_batch)

七、加权指数平均（Weighted Exponential Moving Average, WEMA）

存在一些比梯度下降更快的算法，但是为了学习这些算法，需要提前明白加权指数平均

加权指数平均（WEMA）的核心思想就是在考虑所有历史数据的基础上，通过赋予较新的数据点和旧数据点不同的权重，来计算局部平均值

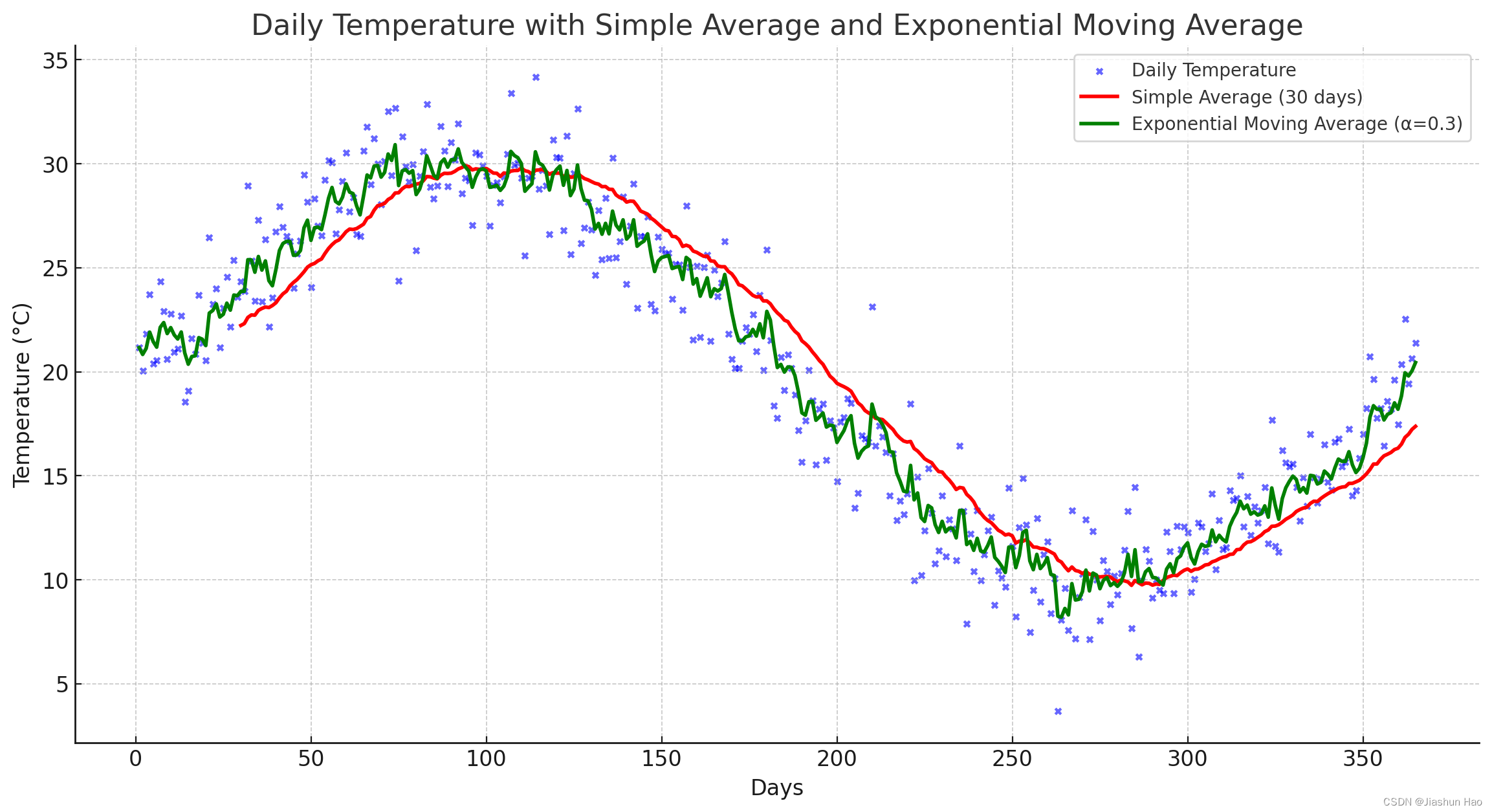
1. 数学公式

$$V_t=\beta V_{t-1}+(1-\beta ){\theta }_t$$
其中
$$\beta =0.9，V_{t-1}为旧数据，{\theta }_t为新观察到的数据点$$
$$结果V_t\approx 前1/(1-\beta )个样本的平均值$$
假设$\beta =0.9$推导出$1/(1-\beta )=10$，那么$V_t$就是以当前起点，约等于前10个样本平均值
假设$\beta =0.5$推导出$1/(1-\beta )=2$，那么$V_t$就是以当前起点，约等于前2个样本平均值

八、带动力的梯度下降（Gradient descent with momentum）

这个算法的主要思想，是计算梯度的指数加权平均，然后使用这个梯度来更新权重

动量方法的核心就是增大过去值的影响力，减小新值的影响，来平滑下降过程，不至于太抖动。同时也可以使用大学习率了。

1. 平滑更新过程：通过累积历史梯度，动量方法能够平滑参数的更新过程，减少在优化过程中的振荡或震荡。这是因为在每一步中，不仅考虑了当前的梯度，还有之前累积下来的梯度方向，使得更新方向更加稳定。
2. 使用更大的学习率：由于动量帮助减少了更新中的随机波动，因此可以使用较大的学习率而不至于让模型的训练过程变得不稳定。较大的学习率可以帮助模型在训练初期快速下降，并在后期通过动量的平滑作用维持稳定。

它的原理很简单，

在持续方向上加速：如果连续多个梯度指向同一方向，动量会累积这个方向上的速度，使得参数更新更快，从而加速收敛。

在反向振荡时减速：如果梯度方向频繁改变（例如在陡峭的“峡谷”地形中），累积的动量可以减缓更新的步伐，从而减少在这些方向上的振荡。

1. 数学公式

动力计算公式：
$$V_t=\beta V_{t-1}+(1-\beta )g_t$$

参数更新公式：
$${\theta }_t={\theta }_{t-1}-\alpha v_t$$

2. 代码公式

1：$V_{dw}$ 和 $V_{db}$ 被初始化为0 , 形状与 $dw,db$ 相同.
2：$\beta$ 恒定为0.9
$$V_{dw}=\beta V_{dw}+(1-\beta )dw$$
$$V_{db}=\beta V_{db}+(1-\beta )db$$
$$W:=W-\alpha V_{dw}$$
$$b:=b-\alpha V_{db}$$

3. 实现代码

L = len(parameters) // 2 # number of layers in the neural networks

for l in range(1, L + 1): #神经网络层数
	#1:使用原始的反向传播计算机dw和db
	dw,db
	
	#2:初始化Vdw和Vdb
	#Vdw =0,Vdb=0
	v["dW" + str(l)] = np.zeros_like(parameters["W" + str(l)])
	v["db" + str(l)] = np.zeros_like(parameters["b" + str(l)])
	
	#3:计算动力
	beta=0.9
	Vdw = beta * Vdw + (1-beta) * dw
	Vdb = beta * Vdb + (1-beta) * db
	
	#4:更新
	w = w - Lambda * Vdw
	b = b - Lambda * Vdb

九、RMSprop（Root Mean Square Propagation）

RMSprop算法通过引入指数加权移动平均（Exponential Moving Average, EMA）来调整每个参数的学习率，从而防止学习率过大或过小。

1. 数学公式

在公式里面额外引入了一个非常小常数$ϵ$，这是为了防止除数为0, 常用的设置为 $ϵ=10^{-8}$。$\beta$ 恒定为0.999

指数加权移动平均计算公式：
$$S_t=\beta S_{t-1}+(1-\beta )g_t^2$$
更新公式：
$${\theta }_t={\theta }_{t-1}-\frac{\alpha }{\sqrt{S_t}+ϵ}{g}_t$$

2. 代码公式

$$S_{dw}=\beta S_{dw}+(1-\beta )d{w}^2$$
$$S_{db}=\beta S_{db}+(1-\beta )d{b}^2$$
$$W:=W-\frac{\alpha }{\sqrt{S_{dw}}+ϵ}dw$$
$$b:=b-\frac{\alpha }{\sqrt{S_{db}}+ϵ}db$$

3. 实现代码

L = len(parameters) // 2 # number of layers in the neural networks

for l in range(1, L + 1): #神经网络层数

	#1:使用原始的反向传播计算机dw和db
	dw,db
	
	#2:初始化Sdw和Sdb
	#Sdw =0,Sdb=0
	S["dW" + str(l)] = np.zeros_like(parameters["W" + str(l)])
	S["db" + str(l)] = np.zeros_like(parameters["b" + str(l)])
	
	#3:计算加权移动
	beta=0.999
	epsilon = 1e-8
	
	Sdw = beta * Sdw + (1 - beta) * (dw ** 2)
	Sdb = beta * Sdb + (1 - beta) * (db ** 2)
	
	#4:更新
	w = w- Lambda * dw / (np.sqrt(Sdw) + epsilon)
	b = b- Lambda * db / (np.sqrt(Sdb) + epsilon)

十、Adam（Adaptive Moment Estimation）

Adam结合了动量法和RMSprop的优点，同时引入了偏差修正，以提高训练的效率和稳定性。

1. 数学公式

可以用它来代替梯度下降算法。$g_t$ 为导数

公式一，动力计算：
$$m_t={\beta }_1{m}_{t-1}+(1-{\beta }_1)g_t$$
公式二，指数计算：
$$v_t={\beta }_2{v}_{t-1}+(1-{\beta }_2)g_t^2$$
公式三：偏差修正：
$${\hat{m}}_t=\frac{m_t}{1-{\beta }_1^t}$$
$${\hat{v}}_t=\frac{v_t}{1-{\beta }_2^t}$$
公式四：更新
$${\theta }_t={\theta }_{t-1}-\frac{\alpha {\hat{m}}_t}{\sqrt{{\hat{v}}_t}+ϵ}$$

2. 代码公式

1：$V_{dw}$ 和 $V_{db}$， $S_{dw}$ 和 $S_{db}$被初始化为0 , 形状与 $dw,db$ 相同.

2：$\beta 1$ 恒定为0.9，$\beta 2$ 恒定为0.999

3： 小常数$ϵ=10^{-8}$

Moment部分：
$$V_{dw}={\beta }_1{V}_{dw}+(1-{\beta }_1)dw$$
$$V_{db}={\beta }_1{V}_{db}+(1-{\beta }_1)db$$

RMSprop部分：
$$S_{dw}={\beta }_2{S}_{dw}+(1-{\beta }_2){dw}^2$$
$$S_{db}={\beta }_2{S}_{db}+(1-{\beta }_2){db}^2$$

偏差修正部分：

为什么要这个？

一开始我们默认的将$V_{dw}$ 和 $V_{db}$， $S_{dw}$ 和 $S_{db}$被初始化为0，这样会导致动量和梯度平方的指数加权移动平均值（EMA）未完全成熟而导致的偏差。我们需要消除这个偏差。

$$V_{dw}^{corrected}=\frac{V_{dw}}{1-{\beta }_1^t}，V_{db}^{corrected}=\frac{V_{db}}{1-{\beta }_1^t}$$
$$S_{dw}^{corrected}=\frac{S_{dw}}{1-{\beta }_2^t}，S_{db}^{corrected}=\frac{S_{db}}{1-{\beta }_2^t}$$

更新部分：
$$W=W-\frac{\alpha V_{dw}^{corrected}}{\sqrt{S_{dw}^{corrected}}+ϵ}$$
$$b=b-\frac{\alpha V_{db}^{corrected}}{\sqrt{S_{db}^{corrected}}+ϵ}$$

3. 实现代码

#1：Vdw，Vdb，Sdw，Sdb 初始化为0，形状和W，b一样
L = len(parameters) // 2 # number of layers in the neural networks
for l in range(1, L + 1): #神经网络层数	
	v["dW" + str(l)] = np.zeros_like(parameters["W" + str(l)])
	v["db" + str(l)] = np.zeros_like(parameters["b" + str(l)])
	s["dW" + str(l)] = np.zeros_like(parameters["W" + str(l)])
	s["db" + str(l)] = np.zeros_like(parameters["b" + str(l)])



#2：动力和RMSprop计算
L = len(parameters) // 2                 # number of layers in the neural networks
v_corrected = {}                         # Initializing first moment estimate, python dictionary
s_corrected = {}                         # Initializing second moment estimate, python dictionary
learning_rate = 0.01, beta1 = 0.9, beta2 = 0.999,  epsilon = 1e-8
grads #存放反向传播的导数

for l in range(1, L + 1):
	#动力
    v["dW" + str(l)] = beta1*v["dW" + str(l)]+(1-beta1)*grads["dW" + str(l)]
    v["db" + str(l)] = beta1*v["db" + str(l)]+(1-beta1)*grads["db" + str(l)]
    
    #动力矫正
    v_corrected["dW" + str(l)] = v["dW" + str(l)]/(1-beta1**t)
    v_corrected["db" + str(l)] = v["db" + str(l)]/(1-beta1**t)
	
	#RMSprop
	s["dW" + str(l)] = beta2*s["dW" + str(l)]+(1-beta2)*grads["dW" + str(l)]*grads["dW" + str(l)]
    s["db" + str(l)] = beta2*s["db" + str(l)]+(1-beta2)*grads["db" + str(l)]*grads["db" + str(l)]
	
	#RMSprop矫正
	s_corrected["dW" + str(l)] = s["dW" + str(l)]/(1-beta2**t)
    s_corrected["db" + str(l)] = s["db" + str(l)]/(1-beta2**t)
	
	#更新
	parameters["W" + str(l)] -= learning_rate * v_corrected["dW" + str(l)]/(np.sqrt(s_corrected["dW" + str(l)])+epsilon)
    parameters["b" + str(l)] -= learning_rate * v_corrected["db" + str(l)]/(np.sqrt(s_corrected["db" + str(l)])+epsilon)
        

十一、学习率衰减（Learning Rate Decay）

学习率是控制模型更新步幅的超参数。

1：过高的学习率可能导致训练过程震荡甚至无法收敛
2：过低的学习率则可能导致训练速度过慢。

学习率衰减的目的是在训练初期使用较大的学习率以快速逼近最优解，然后逐步减小学习率以精细化模型参数，使模型更稳定地收敛到局部或全局最优点。

常用的两个更新公式：

1：阶梯衰减率

$${\eta }_t(学习率)=\frac{{\eta }_0(初始学习率)}{1+\lambda t(迭代次数)}$$

2：指数衰减率

$${\eta }_t(\text{学习率})={\eta }_0(\text{初始学习率})\cdot e^{-\lambda t(\text{迭代次数})}$$

PS、Python技巧

1.随机数 randn 和 rand 的区别

在Python中，特别是在涉及到科学计算和数据处理的库NumPy中，randn和rand函数都用来生成随机数，但它们的用途和输出的随机数类型有所不同：

1. numpy.random.randn:

   • randn函数生成的是服从标准正态分布（均值为0，方差为1的正态分布）的随机数。
   • 可以生成任意形状的数组。
   • 例如，np.random.randn(2, 3)会生成一个2行3列的数组，数组中的每个元素都是从标准正态分布中随机抽取的。

2. numpy.random.rand:

   • rand函数生成的是在区间[0, 1)内均匀分布的随机数。
   • 同样可以生成任意形状的数组。
   • 例如，np.random.rand(2, 3)会生成一个2行3列的数组，数组中的每个元素都是从[0, 1)区间的均匀分布中随机抽取的。

简而言之，主要区别在于：

• randn用于生成符合标准正态分布的随机数。
• rand用于生成符合均匀分布的随机数。

具体到应用:

初始化权重矩阵：randn

Dropout正则化：rand

2.同时设置网络层数

在典型的神经网络实现中，参数字典 parameters 通常包含每一层的权重和偏置，通常以 W1, b1, W2, b2, …, WL, bL 这样的方式命名。

这里 W 代表权重矩阵，b 代表偏置向量，而数字表示对应的层。

比如，对于一个具有 ( L ) 层的神经网络，parameters 可能包含以下键值对：

• W1, b1: 第一层的权重和偏置
• W2, b2: 第二层的权重和偏置
• …
• WL, bL: 第 L 层的权重和偏置

这样，parameters 的键的数量总是 ( 2L )（每一层有两个参数，一个权重矩阵和一个偏置向量）。

因此，len(parameters) 将返回字典中键的总数，即 ( 2L )。用这个总数除以 2 就得到了神经网络的层数 ( L )。

    L = len(parameters) // 2 # number of layers in the neural networks
    for l in range(1, L + 1):
    	#初始化操作。...

3. 多维数组转一维向量

flatten 操作通常用于将多维数组（如矩阵或张量）变为一维数组（向量）

import numpy as np

a=np.random.rand(3,3)
print (a)
# [[0.81326486 0.08026124 0.38529666]
#  [0.26521685 0.2712353  0.37634291]
#  [0.70843229 0.34048282 0.32902673]]

a=a.flatten()
print(a)
#[0.81326486 0.08026124 0.38529666 0.26521685 0.2712353  0.37634291 0.70843229 0.34048282 0.32902673]

4. 数组逐元素平方

np.square 是 NumPy 库中的一个函数，用于逐元素计算输入数组中每个元素的平方。该函数返回一个新数组，其中包含输入数组的每个元素的平方值。这个操作是逐元素的，因此对于输入数组中的每个元素，都有对应的平方值。

import numpy as np
a=np.random.rand(3,3)
print(a)
# [[0.60829188 0.462002   0.53711763]
#  [0.45887545 0.0317922  0.96084417]
#  [0.62161485 0.53259823 0.95088835]]

a=np.square(a)
print(a)
# [[0.37001901 0.21344585 0.28849535]
#  [0.21056668 0.00101074 0.92322152]
#  [0.38640502 0.28366088 0.90418865]]

5. 拷贝数组矩阵

a=np.copy(b) 用于创建一个数组的拷贝

import numpy as np
a=np.random.rand(3,3)
print(a)
# [[0.60829188 0.462002   0.53711763]
#  [0.45887545 0.0317922  0.96084417]
#  [0.62161485 0.53259823 0.95088835]]

b=np.copy(a)
print(b)
# [[0.60829188 0.462002   0.53711763]
#  [0.45887545 0.0317922  0.96084417]
#  [0.62161485 0.53259823 0.95088835]]

6.随机打乱数据

6.1.随机打乱数据：生成指定范围的随机排列的列表

permutation = list(np.random.permutation(m))用于生成一个从0 到 m 的随机排列的列表

import numpy as np

m=5

permutation = list(np.random.permutation(m))

print(permutation) #[2, 4, 3, 1, 0]

6.2.随机打乱数据：数组切片语法

切片的基本语法是 start:stop:step，其中：

start：切片开始的索引（包含）。
stop：切片结束的索引（不包含）。
step：步长（可选，默认为 1）。

# 创建一个示例数组
import numpy as np
data = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])

# 提取前5个元素
print(data[:5])  # 输出: [1 2 3 4 5]

# 提取从索引2到索引7的元素（不包含索引7）
print(data[2:7])  # 输出: [3 4 5 6 7]

# 提取从索引2到索引7的每隔一个元素
print(data[2:7:2])  # 输出: [3 5 7]

# 提取数组的最后3个元素
print(data[-3:])  # 输出: [ 8  9 10]

还可以反转数组：

# 反转数组
print(data[::-1])  # 输出: [10 9 8 7 6 5 4 3 2 1]

用于2D数组：: 代表所有，截断提取想要的数

# 创建一个2D数组
matrix = np.array([[1, 2, 3],
                   [4, 5, 6],
                   [7, 8, 9]])

# 提取第一行
print(matrix[0, :])  # 输出: [1 2 3]

# 提取第二列
print(matrix[:, 1])  # 输出: [2 5 8]

# 提取前两行
print(matrix[:2, :])  # 输出: [[1 2 3]
                      #       [4 5 6]]

# 提取前两列
print(matrix[:, :2])  # 输出: [[1 2]
                      #       [4 5]
                      #       [7 8]]

# 提取第二行第二列以后的所有元素
print(matrix[1:, 1:])  # 输出: [[5 6]
                       #       [8 9]]

6.3.随机打乱数据：高级索引：使用整数数组或列表来进行索引重新排序

使用指定范围的随机排列的列表和数组切片，可以将数组中的元素重新排序

import numpy as np

#原始数据
array=np.array([[1, 2, 3, 4, 5],
                [100, 200, 300, 400, 500],
                [1000,2000,3000,4000,5000]]
              )


x=[0,3,1,4,2]
ac=array[:,x]  # 每一行的数据按照指定的顺序重新排列
print(ac)
# [[   1    4    2    5    3]
#  [ 100  400  200  500  300]
#  [1000 4000 2000 5000 3000]]

y=[1,0,2]
ac=array[y,:] # 每一列的数据按照指定的顺序重新排列
print(ac)
# [[ 100  200  300  400  500]
#  [   1    2    3    4    5]
#  [1000 2000 3000 4000 5000]]

7. 向上取整和向下取整

向上取整，使用math.ceil()，入小数为1

import math

a=1.23

b=math.ceil(a)

print(b) #2

向下取整，使用math.floor()，舍弃小数

import math

a=1.23

b=math.floor(a)

print(b) #1