文章目录
第六章 二次型
6.1 二次型及其标准形
6.1.1 概念
二次型:什么叫二次型?它是一个多元函数,每一个变量累积的次数为2次。即n个变量的一个二次齐次多项式
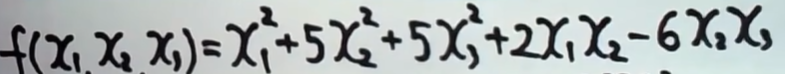
f
(
x
1
,
x
2
,
.
.
.
,
x
n
)
=
∑
i
=
1
n
∑
j
=
1
n
a
i
j
x
i
x
j
=
x
T
A
x
f(x_1,x_2,...,x_n) = \sum_{i=1}^{n}\sum_{j=1}^{n} a_{ij}x_{i}x_j = x^TAx
f(x1,x2,...,xn)=i=1∑nj=1∑naijxixj=xTAx
平方项系数在主对角线上,混合项的系数在除2在对角线对称的地方。
标准形:只有二次型的平方项,而不存在混合项。
规范形:标准形的平方项系数只有+1,-1或者0,则称为二次型的规范形。

正惯性指数:标准形里面正平方项的个数,记作p
负惯性指数:标准形里面负平方项的个数,记作q

二次型的秩:也就是矩阵A的秩。
r
(
f
)
=
r
(
A
)
=
p
+
q
r(f) = r(A) = p+q
r(f)=r(A)=p+q
坐标变换:将通过y来表示x。可以写成方程组的形式:
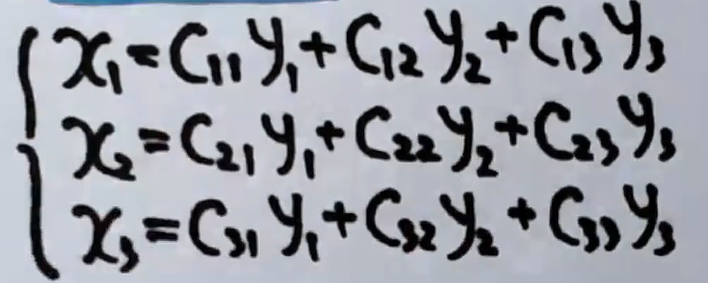
注意,这里的C矩阵的行列式不能等于0
不过一般不写成方程组,一般写成矩阵乘法的形式
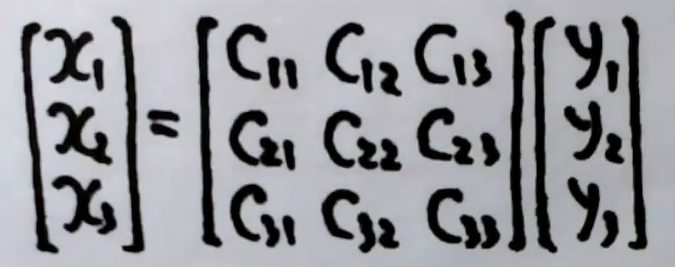
再写得简单一点,可以写成
x
=
C
y
x = Cy
x=Cy
其中,C是可逆矩阵。
例子:下面的方程组不是坐标变换
{
y
1
=
x
1
+
x
2
y
2
=
x
2
−
x
3
y
3
=
x
1
+
x
3
\left\{ \begin{aligned} y_1 & =x_1 + x_2 \\ y_2 & = x_2-x_3 \\ y_3 & = x_1 + x_3 \end{aligned} \right.
⎩
⎨
⎧y1y2y3=x1+x2=x2−x3=x1+x3
因为行列式C = 0
矩阵合同:经过坐标变换,A和B合同。

6.1.2 合同基本性质
-
反身性:A和A自己合同
-
对称性:A合同B,则B合同A
-
传递性:A合同B,B合同C,则A合同C
-
充要条件:两个矩阵合同,它们的充要条件是正惯性指数相同,负惯性指数相同。(即特征值的符号相同)
A 合同 B < = > P A = P B 且 q A = q B A 合同B <=> P_A = P_B 且 q_A = q_B A合同B<=>PA=PB且qA=qB
-
定理1:对于任一n元二次型f = xTAx,存在正交变换(配方法就不行)x=Qy,其中Q是正交阵,使得二次型f化为标准形
Q − 1 A Q = Q T A Q = A 的对角矩阵 = λ 1 y 1 2 + λ 2 y 2 2 Q^{-1}AQ = Q^TAQ = A的对角矩阵 = λ_1y_1^{2} + λ_2y_2^2 Q−1AQ=QTAQ=A的对角矩阵=λ1y12+λ2y22
此时A和它的对角矩阵,既相似,又合同 -
定理2:任意给定一个实对称矩阵A, 一定存在可逆矩阵C, 使得CTAC为对角矩阵.
- 配方法,不会考太难
- 正交变换法:较难
-
惯性定理:一个二次型f = xTAx经过坐标变换后转成标准形,它的正惯性指数和负惯性指数都是一样的。
求坐标变换 == 求Q矩阵 == 求A的特征向量 == 是不是要单位向量,正交垂直
任何一个二次型也可以通过配方法,实现化成标准形。用坐标变换,把标准形化成规范形。
6.1.3 题型
-
给出二次型,写出对应的二次型矩阵
注意对称性,系数除2
-
用配方法化二次型
把所有含x的项配成一个完全平方,从x1开始配。引入新变量后得到f的标准形
-
用正交变化化 二次型 为标准形
- 写出二次型矩阵A
- 求A的特征值,代入特征值得到对应的特征向量
- 改造特征向量γ1,γ2,γ3(正交化,单位化)
- 构建正交矩阵Q = (γ1,γ2,γ3)
-
给出二次型,求对应的正惯性指数
-
写出二次型矩阵A,计算特征行列式|λE - A|=0,求特征值λ。根据特征值的正负个数求得。
-
或根据配方法得到的标准形看出正负惯性指数。
-
-
给出矩阵A,判断与之合同的矩阵B
AB合同,则正负惯性指数相同。
6.2 正定二次型
6.2.1 概念

理解:只要x不等于0,二次型一定严格大于0
6.2.2 定理
-
判定矩阵的正定性:计算所有的特征值>0即可。

-
可逆线性变换 不会改变 二次型的正定性
-
f 正定的充要条件:
- A的正惯性指数 p = n
- A和单位矩阵E合同
- A = DTD ,其中D是一个可逆的矩阵
- A的全部特征值 > 0
- A的全部顺序主子式 > 0
-
f 正定的 必要条件
- A的主对角元素 aii > 0
- A的行列式 |A| > 0
6.3 补充:解题技巧
6.3.1 惯性定理的理解

6.3.2 矩阵合同的充要条件


注意:这里“相似必然合同”的前提是实对称矩阵,更确切的单句说法应该是“实对称矩阵相似一定合同”。
6.3.3 配方法的坐标变换必须可逆
配方法和下一个正交变化都是化标准型的方法。

6.3.4 正交变化化标准型 (😰难)
- 把 二次型f(x) 转化成 二次型矩阵A
- 求二次型矩阵对应的特征值 λ1、λ2、λ3。
可以使用|λE - A|=0 - 把特征值凑成一个对称阵
- 反代得到对应的


6.3.5 求二次型对应的矩阵
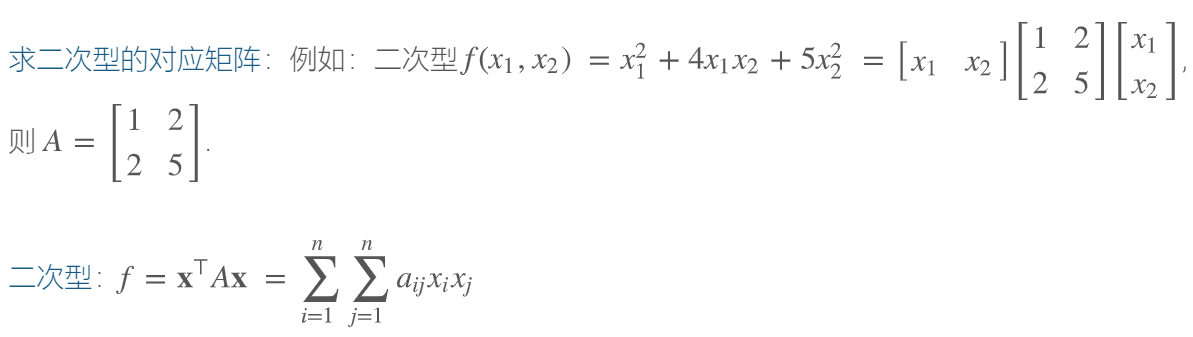
6.3.6 曲面集合
柱面

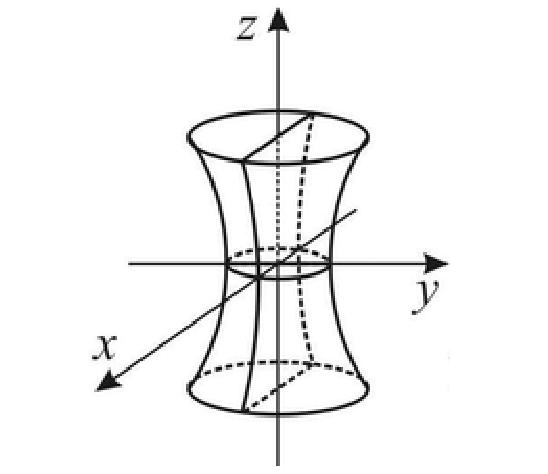
单叶双曲面

下图给出的单叶双曲面是直立的,为上述第一行的方程:
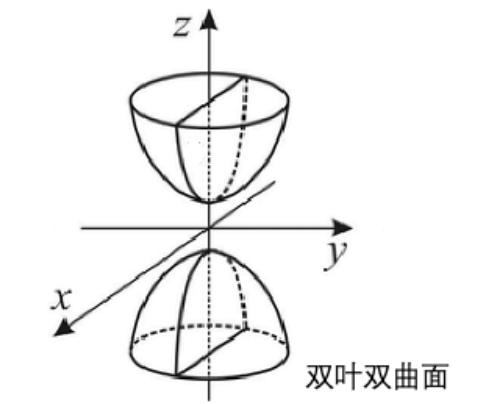
双叶双曲面
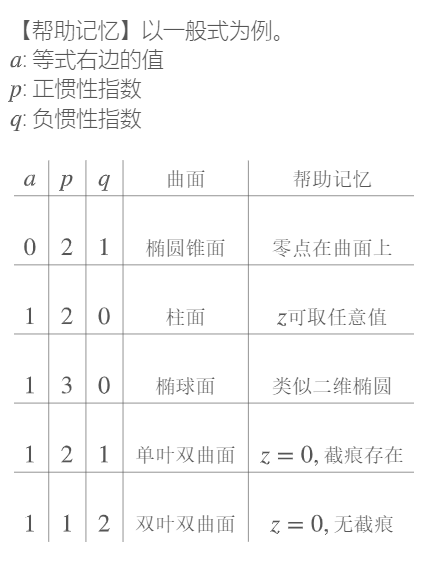
辅助记忆
椭球面、单叶双曲面 及 双叶双曲面的惯性指数的符号差分别为 3、1、-1.
如果符号差为2,则代表是柱面。
6.3.6 证明XX矩阵是正定矩阵
假设需要证明
A
T
A
是正定矩阵
A^T A是正定矩阵
ATA是正定矩阵
第一步:证对称
注意:正定矩阵是二次型的对应矩阵,须先证明对称。
即先说明:这个矩阵的转置是它自己
(
A
T
A
)
T
=
A
T
(
A
T
)
T
=
A
T
A
(A^T A)^T = A^T(A^T)^T = A^T A
(ATA)T=AT(AT)T=ATA
第二步:根据矩阵是否抽象,选择不同的方式:
- 如果给出的是抽象矩阵,一般用定义证明:
对于任意非零向量 x ,恒有 x T ( A T A ) x > 0 对于任意非零向量x,恒有x^T(A^TA)x>0 对于任意非零向量x,恒有xT(ATA)x>0 - 如果给出的是具体的矩阵,就可以算特征值:
所有特征值 λ > 0 所有特征值\lambda > 0 所有特征值λ>0

























 2819
2819











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










