记录:学习stable diffusion模型原理,需要学习VAE、CLIP、Diffusion、Unet、Transformer
一、VAE:
(图源来自原论文和李宏毅老师的视频)
1.流程图示
观测数据X输入到MLP编码器里(图中绿色NN),输出隐向量z(多元高斯分布)的每一个维度的期望m和方差,通过与采样自标准正态的噪音
运算之后,输入到MLP解码器里(图中蓝色NN),解码器会输出条件概率分布
的参数,并利用这些参数采样还原数据X。
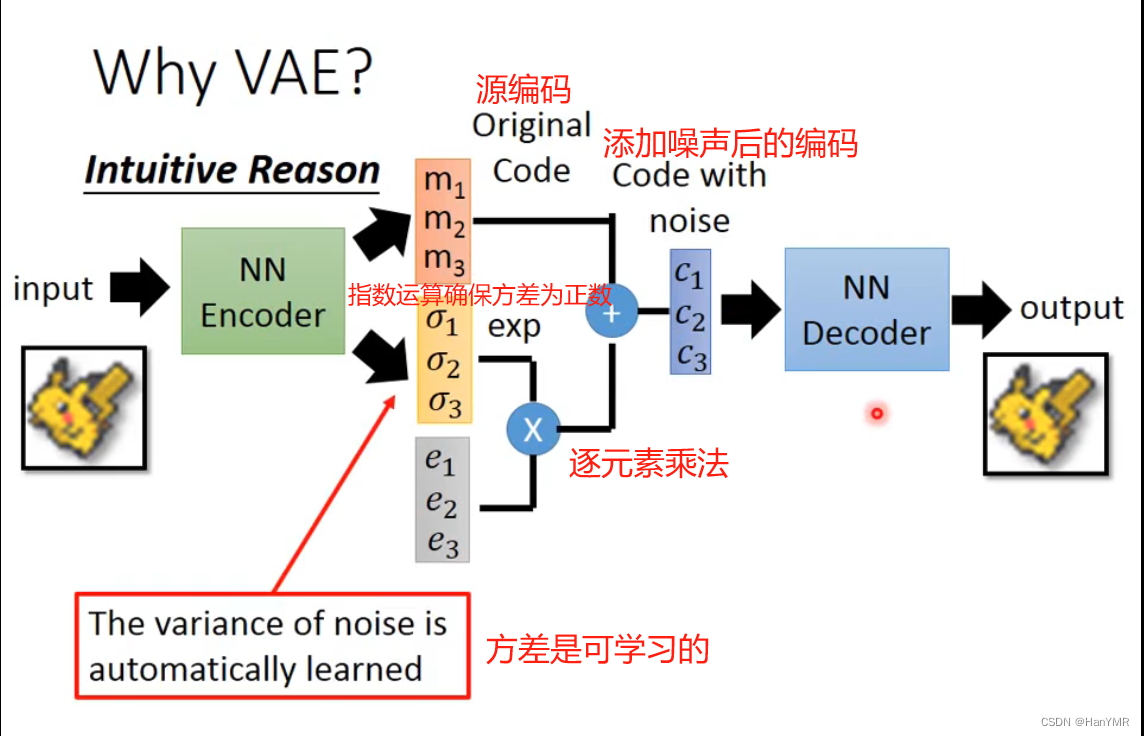
2.模型开始
李老师的视频里介绍了一维高斯混合模型,原理是多个正态分布可以叠加成为任一分布。P(x)是数据x的分布概率,而z上任取一点就代表其中一条蓝色的高斯分布,取遍z上所有的点就可以模拟出x的分布。

论文给出的图解
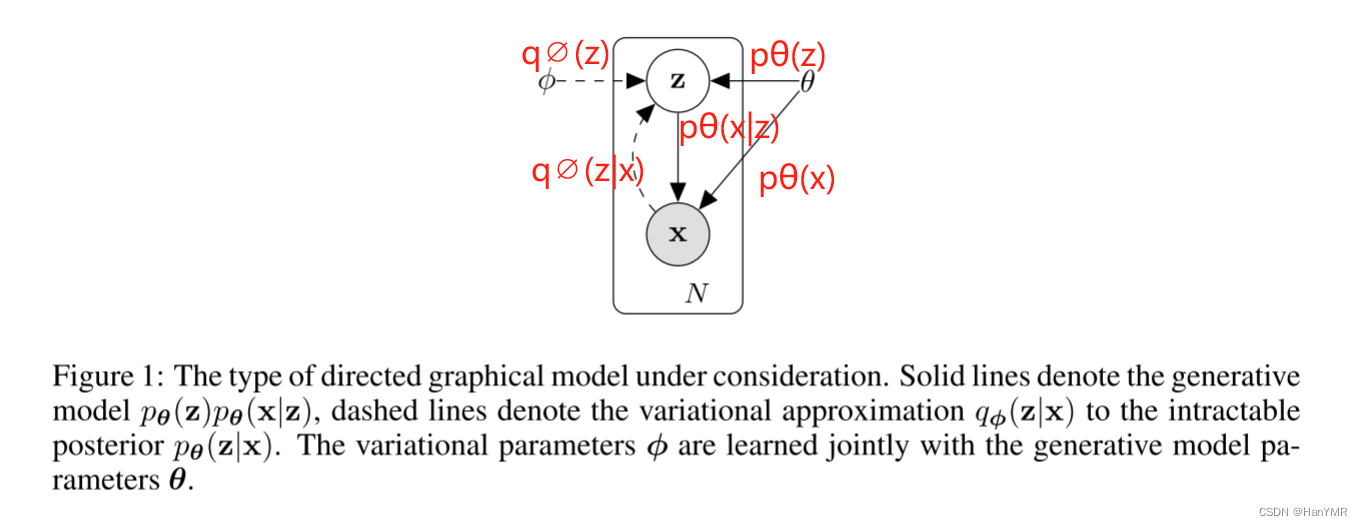
是独立同分布的样本数据集,
是生成的连续随机隐变量。
假设数据是由z随机生成的,该过程包括两个步骤:
(1) 从先验分布中生成一个值
;
(2) 从条件分布中生成一个值
;
先验分布:,由于难以计算,用
近似表示(变分法)。
和
会在训练时一起学习。
指编码器。负责将输入的数据映射到隐空间中。
后验分布:。
指解码器。负责从隐空间中采样,重构出原始的数据。
但真实参数以及潜在变量
的值都是隐藏的。于是论文开始探索解决之法。
3.目标函数
化简过程:(手推了一下)
原文中用代替第二项,写作:

4.目标函数结果分析
第一项KL散度是近似分布与真实分布的一致性,因为这一项非负,所以我们需要求满足下界取最大值时的参数
和
,这时会影响
越来越小,也就是能找到与真实分布非常相近的的近似分布。

对于第二项,原文中运算过程:
于是需要找到和
继续分析
①对于,就是要调MLP编码器里(图中绿色NN)的参数,使它产生的z的分布能接近
②对于,在①的条件下,只需要调整MLP解码器里(图中蓝色NN)的参数,使它产生的x的分布期望接近于样本x,也就是说使生成的x接近于输入的x。

分析结果
论文最后举的VAE例子中给出了假设和代数结果:(看不下一点推导,干脆直接看结果)
①假设,是一个多元高斯分布,中心化(
)且在每个维度上的方差都一样(相同分布),
表示单位矩阵。
②根据数据的类型(实数或二进制)被建模为多元高斯分布或伯努利分布,其分布参数通过输入
到MLP解码器里计算得出。
③出于的不可解性,假设这个真实的
近似于对角协方差矩阵的高斯分布,那么可以得出近似分布
:

注:均值和标准差近似和
是MLP编码器的输出
④隐变量 是具有随机性,引用了重参数化技巧这个节点的随机性移出变成确定性,让梯度参数可以反向传播。
由以上假设可以将(1)式中的第二项近似为:
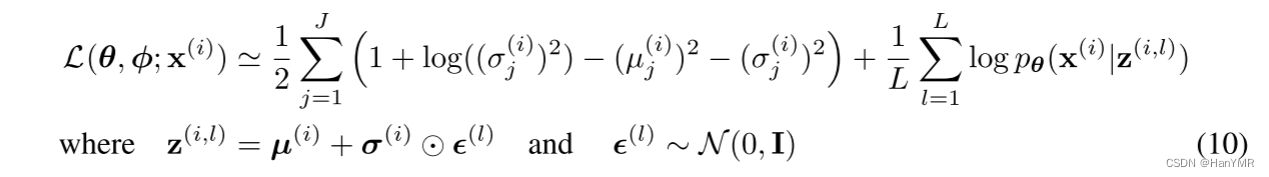
注:用蒙特卡洛法采样了L次,式子中指对
的第
个分量进行第
次采样
5.知识点
①信息量:信息量的多少是与事件
发生概率大小成反比。
②信息熵=熵=概率期望:
③交叉熵:,衡量两个概率分布之间差异。
④KL散度=相对熵=交叉熵-信息熵:,衡量两个概率分布相似度。
⑤概率归一性:对任意分布,都有
⑥全概率:
⑦条件概率:,事件z在另外一个事件x已经发生条件下的发生概率。
⑧泛函数:泛函的输入是一个函数,输出是一个实数或复数。
⑨重参数:重参数化技巧可以确保在进行随机采样时,梯度信息能够被保留,原理是任意一个高斯分布可以分解为关于标准正态分布的函数。
6.之后要看的
理论:勉强看得懂函数推导以及优化策略,但是,因为之前看基础就还没到卷积,跑去匆匆忙忙去看论文找方向,所以这一次要看卷积、循环、transformer。如果有空余还要看GAN。
代码:下一步除了VAE的代码,还要简单实现一下卷积。
论文:得重新找找方向,被sora打了个措手不及。























 2279
2279

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








