详细阐述基于时间的反向传播算法（Back-Propagation Through Time,BPTT）

上一节我们说了详细展示RNN的网络结构以及前向传播，在了解RNN的结构之后，如何训练RNN就是一个重要问题，训练模型就是更新模型的参数，也就是如何进行反向传播，也就意味着如何对参数进行求导。本篇内容就是详细介绍RNN的反向传播算法，即BPTT。

---

首先让我们来用动图来表示RNN的损失是如何产生的，以及如何进行反向传播，如下图所示。

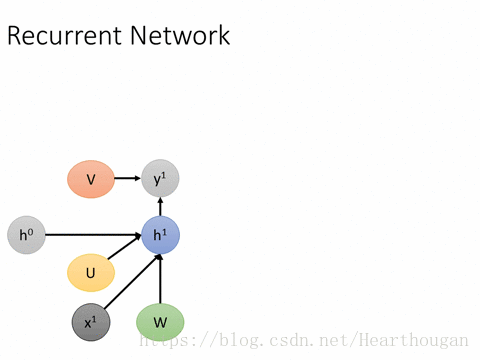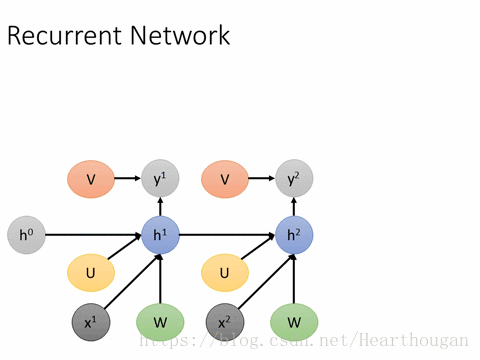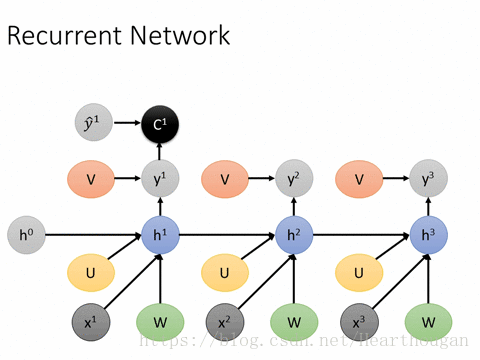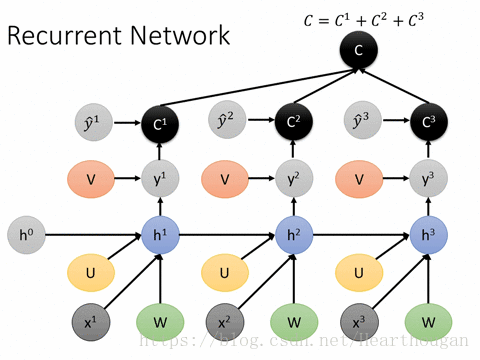
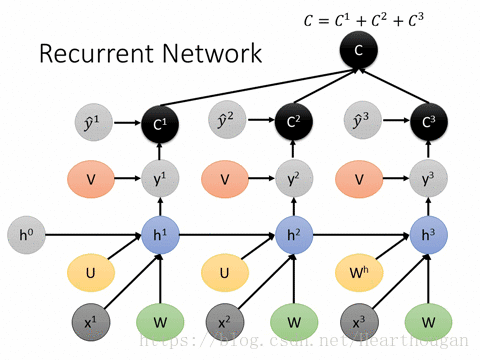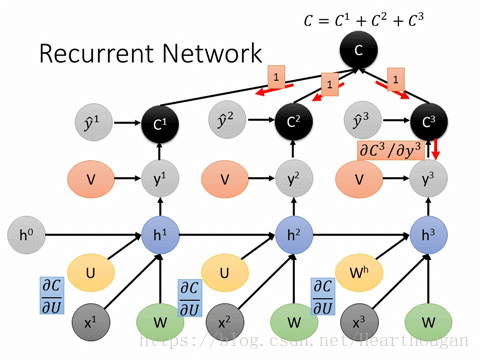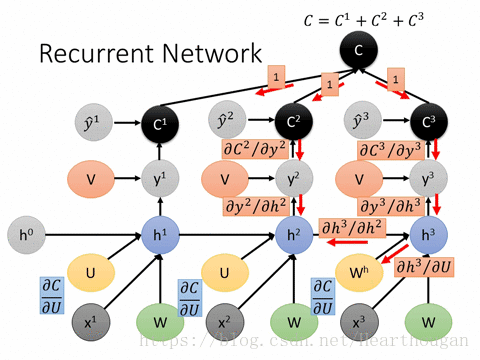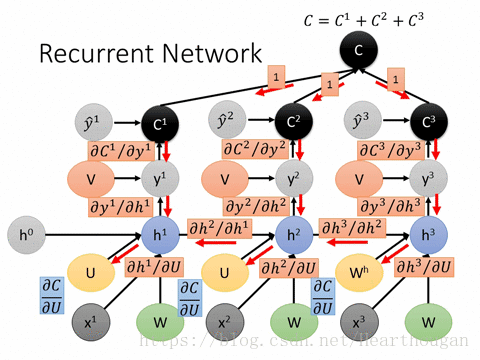
上面两幅图片，已经很详细的展示了损失是如何产生的， 以及如何来对参数求导，这是忽略细节的RNN反向传播流程，我相信已经描述的非常清晰了。下图(来自trask)描述RNN详细结构中反向传播的过程。

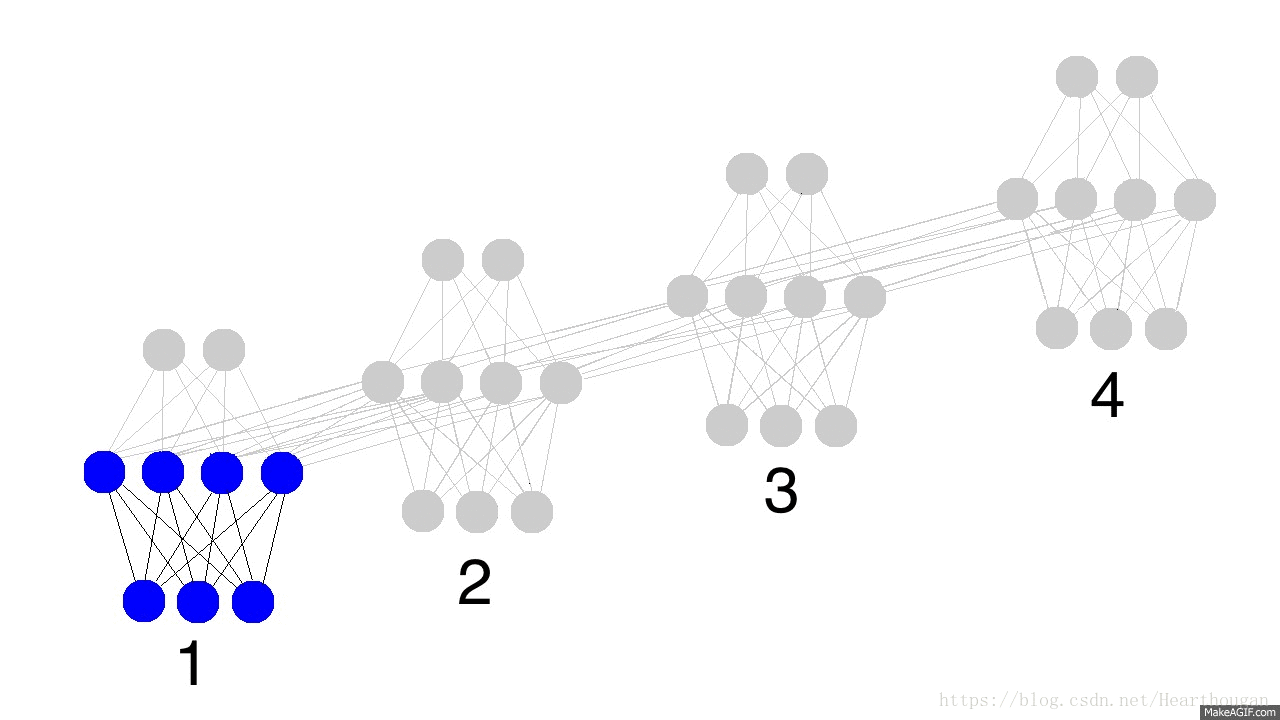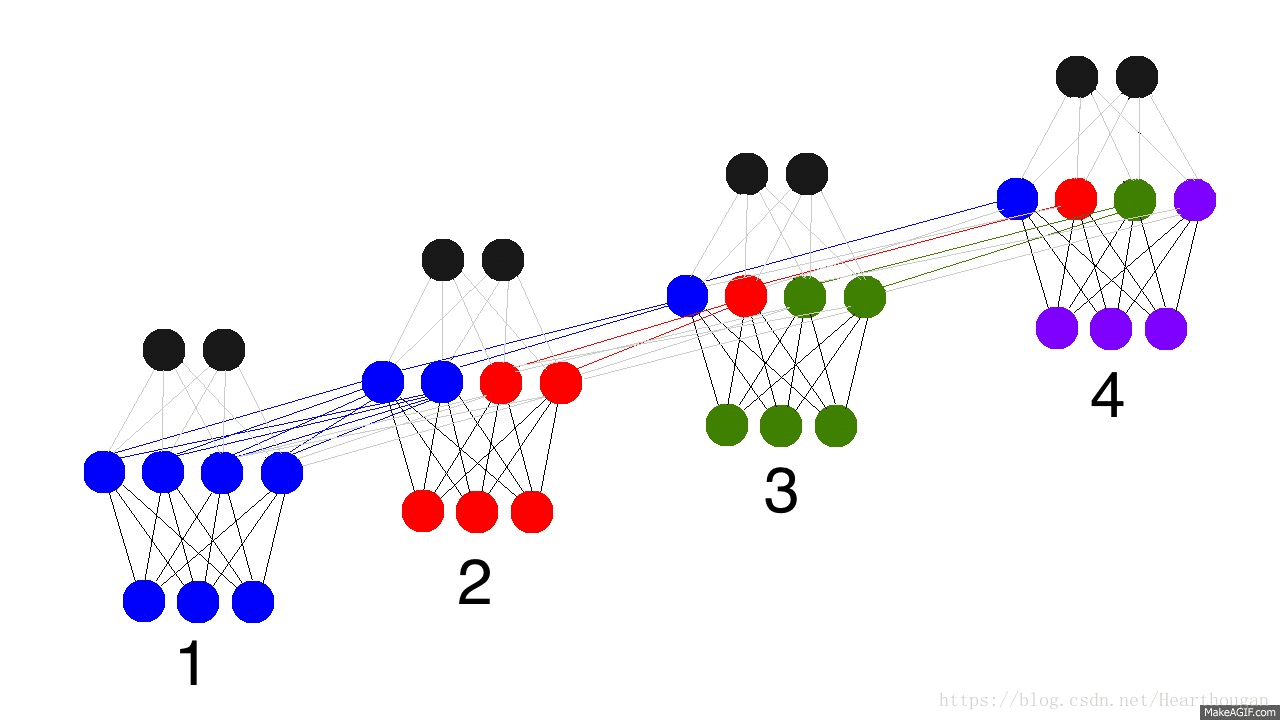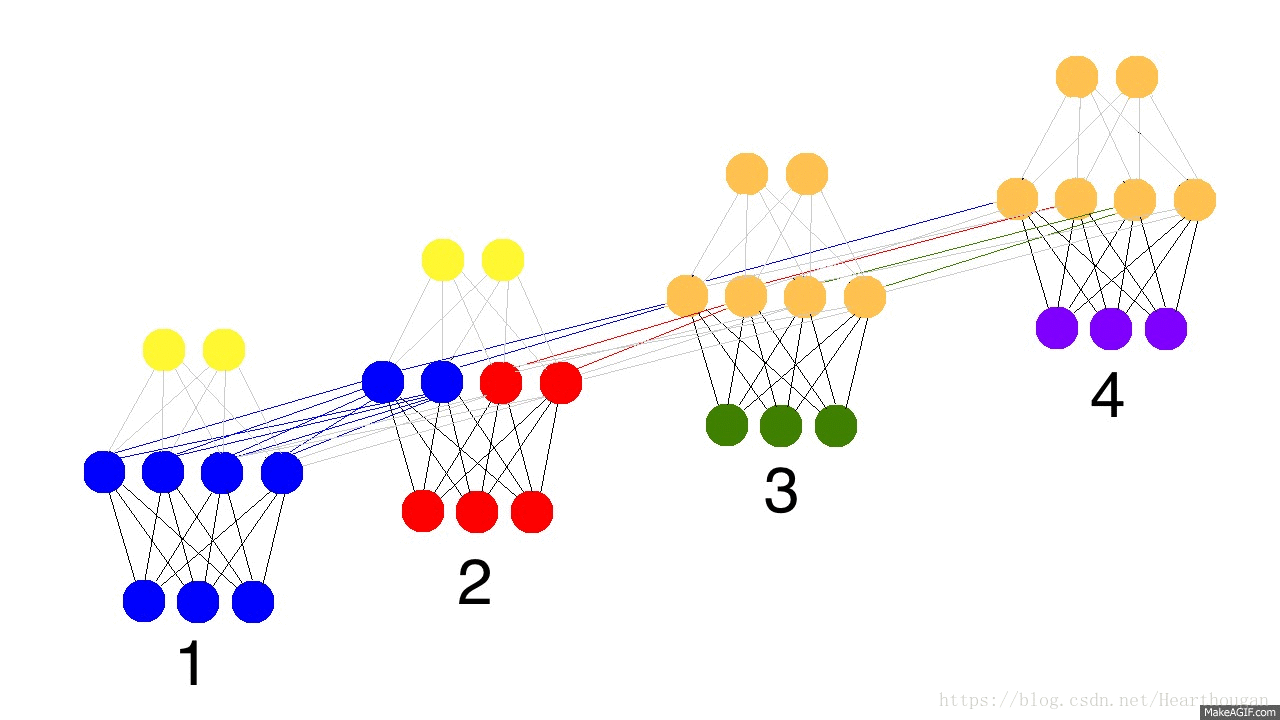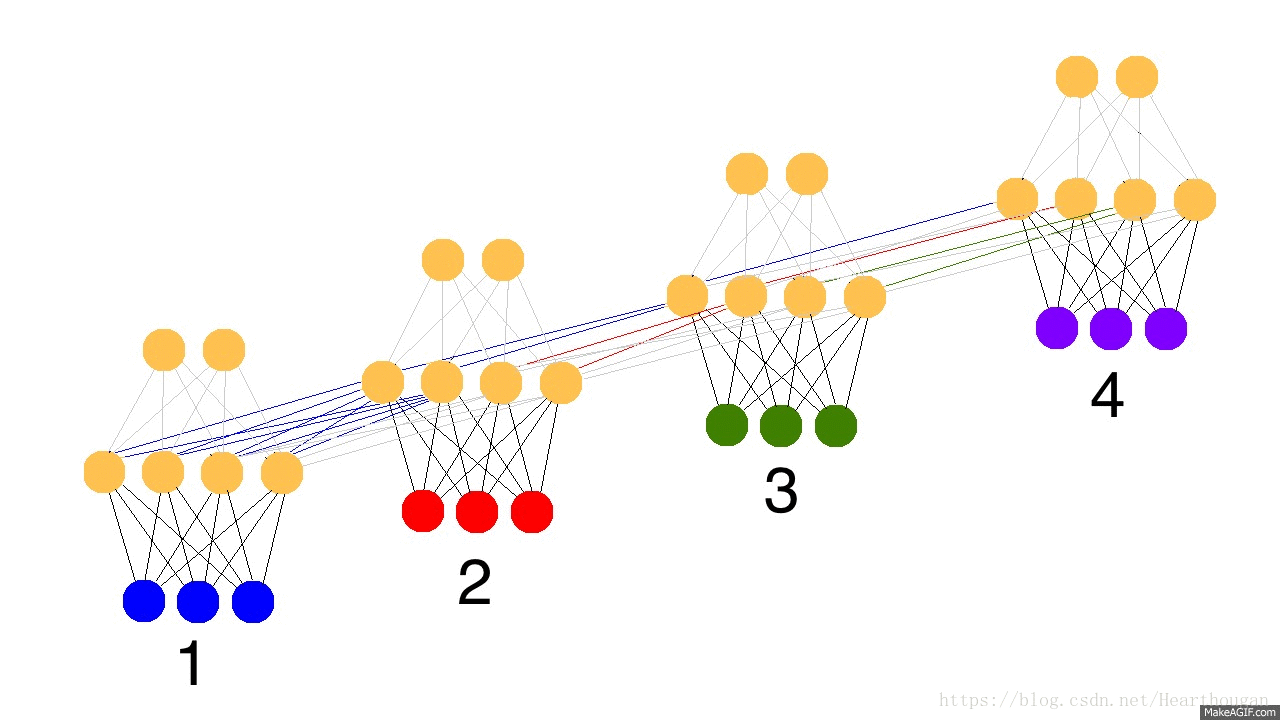
有了清晰的反向传播的过程，我们接下来就需要进行理论的推到，由于符号较多，为了不至于混淆，根据下图，现标记符号如表格所示：

公式符号表

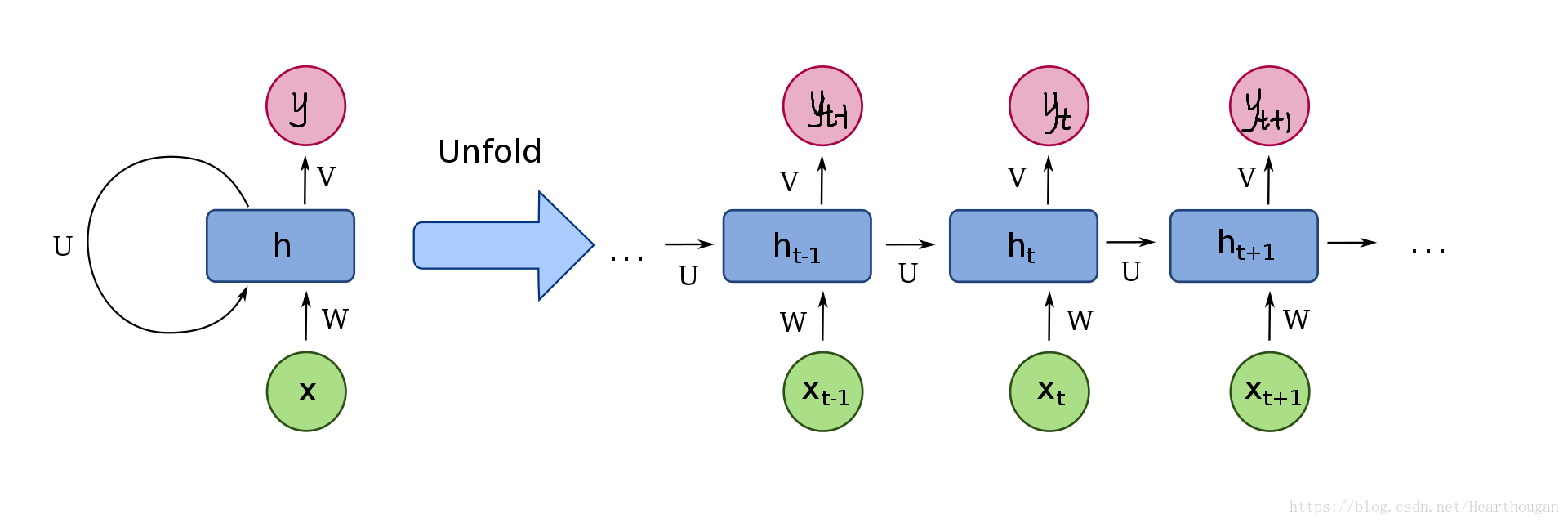
符号	含义
	输入向量的大小（one-hot长度，也是词典大小）
	输入的每一个序列的长度
	隐藏层神经元的个数
	样本集合
	第时刻的输入
	第时刻经过Softmax层的输出。
	第时刻输入样本的真实标签
	第时刻的损失函数，使用交叉熵函数，
	序列对应的损失函数: RNN的反向传播是每处理完一个样本就需要对参数进行更新，因此当执行完一个序列之后，总的损失函数就是各个时刻所得的损失之和。
	第个时刻RNN隐藏层的输入。
	第t个时刻RNN隐藏层的输出。
	输出层的输入，即Softmax函数的输入
	输入层与隐藏层之间的权重。
	上一个时刻的隐藏层 与 当前时刻隐藏层之间的权值。
	隐藏层与输出层之间的权重。

                                                                     

我们对参数求导比较方便，只有每一时刻的输出对应的损失与相关，可以直接进行求导，即：

                                                  

                                                 

要对参数进行更新，就不那么容易了，因为参数虽是共享的，但是他们不只是对第刻的输出做出了贡献，同样对时刻隐藏层的输入做出了贡献，因此在对参数求导的时候，需要从后向前一步一步求导。

假设我们在对时刻的参数求导，我们利用链式法则可得出：

                                                                   

                                                                    

                                                                    

我们发现对进行求导的时候，都需要先求出，因此我们设：

                                                                         

那么我们现在需要先求出，则：

                                                                        

                                                                   

注：在求解激活函数导数时，是将已知的部分求导之后，然后将它和激活函数导数部分进行哈达马乘积。激活函数的导数一般是和前面的进行哈达马乘积，这里的激活函数是双曲正切，用矩阵中对角线元素表示向量中各个值的导数，可以去掉哈达马乘积，转化为矩阵乘法。

则：

                                                                

我们求得，之后，便可以回到最初对参数的求导，因此有：

                                                           

                                                            

                                                           

有了各个参数导数之后，我们可以进行参数更新：

                                                          

                                                           

                                                          

                                                           

                                                          

---

参考：

刘建平《循环神经网络(RNN)模型与前向反向传播算法》

李弘毅老师《深度学习》