斯坦福出的,双曲空间上的GCN,有点抽象,但还是想啃啃。
原文地址:https://arxiv.org/abs/1910.12933v1
GCN将图上的节点映射到欧式空间,在映射无标度网络或分层结构时会失真,双曲几何提供了一个解决方案,因为它能保证有很小的失真。但是,将GCN扩展到双曲几何上有很多挑战,因为不清楚如何在双曲空间上定义神经网络算子,如特征转换和聚合。另外,由于输入特征通常是欧式空间的数据,不清楚如何以正确的曲率将特征转换为双曲嵌入。本文提出HGCN,聚合GCN和双曲几何的表达能力来学习无标度图或分层图中的节点表示。得到双曲空间中双曲模型上的GCN算子,在每一层中用不同的可训练的曲率将欧式输入特征转化为双曲空间中的嵌入。实验表明HGCN能学习分层结构,即使在维度很低的情况下也能表现良好。
1Introduction
GCN是图表示学习的SOTA的模型,它将图中的节点映射到欧式空间中的点。但是,很多现实的图,如蛋白质交互图和社交网络,表现为无标度图或分层结构,而GCN中所用的欧式嵌入在这样的图中经常有高度失真。无标度图通常有树形结构,在这样的结构中,图的体积(以一个中心节点为中心,某个半径范围内的节点数量)以半径的指数级增长,而欧式空间中球的体积只以半径的多项式级增长,这就造成高度失真的嵌入。而在双曲空间中,球的体积是半径的指数。
双曲几何在嵌入无标度图和分层图时能保证很少的失真。但现有的双曲嵌入技术仅考虑图结构,没有利用丰富的节点特征。与深度模型如GCN相比,浅的(shallow)嵌入没有考虑接节点的特征,缺乏可扩展性,并且不具备归纳的特性。另外,在双曲空间上进行优化也是一大挑战。
尽管将GCN扩展到双曲几何上可能会开发出更可信和更精确的模型,但也存在一些挑战:(1)输入节点通常是欧式的,目前还不清楚如何最优地将其转化为双曲神经网络的输入;(2)不清楚如何进行数据聚合,这是在双曲空间中进行信号传递很关键的一步;(3)在GCN的每一步选择什么样的曲率的双曲空间也是很难做决定的。
本文解决了以上问题并提出HGCN,一类能结合GCN和双曲几何表达能力的图表示学习模型。主要贡献为以下三点:
(1)得到了如何将以欧式方式输入的特征转化为双曲输入的核心操作
(2)引入了双曲基于注意力机制的聚合方案,能捕获网络的分层结构
(3)在HGCN的不同层用可训练的曲率的双曲空间进行特征转换,来学习低失真的双曲嵌入
在不同的层用不同的双曲空间进行特征转换使得HGCN能找到隐层最佳的几何结构。本方法联合训练双曲图卷积算子、每一层的曲率和双曲注意力。
与欧式GCN相比,HGCN在分层的图数据上有更强的表达能力。
2相关工作
图表示学习属于几何深度学习的范畴,主要有两种方法:直推式的浅式嵌入(Transductive, shallow embeddings
),和 归纳的GCN.
直推式的方法试图通过最小化一个重建错误来实现节点嵌入的优化。直推式的嵌入有以下的缺点:1)它们没有利用丰富的节点特征,2)这些方法是直推式的,所以不能用于新的图上,3)可扩展性差,因为随着节点数量的增加,它们的参数是线性增长的。
欧式GNN:欧式GNN的主要缺点是在建模无标度图或者有分层结构的图时会造成严重失真。
双曲几何已经应用于很多的神经网络来解决计算机视觉和NLP问题,双曲神经网络2018年才有人提出。而2019年的NIPS就出现了两篇HGCN(注:会不会掀起一层浪?)
3背景知识
令图 表示一个图,其中
表示一个图,其中 是节点集,
是节点集, 是边集合,令
是边集合,令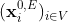 是d维的输入节点特征,其中 0 指的是第一层,E 指的是节点特征是欧式空间中的。图表示学习的目标是学习节点到嵌入向量的映射:
是d维的输入节点特征,其中 0 指的是第一层,E 指的是节点特征是欧式空间中的。图表示学习的目标是学习节点到嵌入向量的映射:
其中 .这些其中嵌入应该既能同时表示节点的语义信息和结构信息,并且能做为下游任务的输入。
.这些其中嵌入应该既能同时表示节点的语义信息和结构信息,并且能做为下游任务的输入。
GCN:令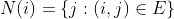 表示节点
表示节点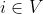 的邻居,
的邻居,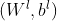 是第
是第  层的参数,
层的参数, 是非线性激活函数,一般的GCN中信号的传递规则为:
是非线性激活函数,一般的GCN中信号的传递规则为:
其中的聚合权重  可以通过不同的机制获得。多层的信号传递能将信号传到网络邻居上。不同于浅的模型,GCN用到了节点特征且具有归纳特性,能应用到unseen节点上。
可以通过不同的机制获得。多层的信号传递能将信号传到网络邻居上。不同于浅的模型,GCN用到了节点特征且具有归纳特性,能应用到unseen节点上。
双曲空间上的双曲面模型(除了双曲面模型应该还有其他模型呢?):双曲几何是HGCN的基本前提,双曲几何是一类具有负曲率的非欧几何,其中的曲率度量一个几何对象偏离平面的程度。这里研究其中的双曲面模型,因为它简单且有很好的性质。
双曲面流形:令 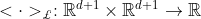 表示闵可夫斯基内积,
表示闵可夫斯基内积,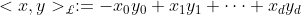 . 则d维的负曲率为
. 则d维的负曲率为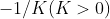 的双曲面流形定义为:
的双曲面流形定义为:
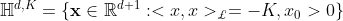
双曲面流形上点  的切空间的定义为:
的切空间的定义为:
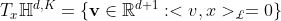
对于切空间 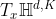 中的两个点
中的两个点 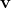 和
和
 ,
, 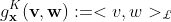 是黎曼度量,
是黎曼度量,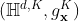 曲率为
曲率为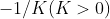 的黎曼流形。
的黎曼流形。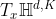 是双曲流形在点
是双曲流形在点 的一阶局部近似且约束到
的一阶局部近似且约束到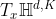 上的闵可夫斯基内积是正的。
上的闵可夫斯基内积是正的。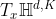 中点的范数为
中点的范数为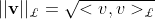
测地线和距离:测地线和距离类似于图中的最短路径或欧式空间中两点间的距离,它在图嵌入算法中很重要,因为一般的优化目标是最小化连接点间的测地线。令 ,
,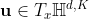 且
且  是unit-speed的,即
是unit-speed的,即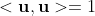 ,则有如下命题:
,则有如下命题:
命题1:令 ,
,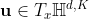 且
且  是unit-speed的,则唯一的满足
是unit-speed的,则唯一的满足 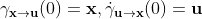 的unit-speed测地线为
的unit-speed测地线为
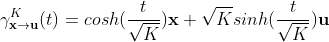
而 中两点
中两点 实质距离为
实质距离为
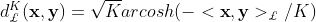
指数映射和log映射:切空间和双曲空间之间的映射通过指数映射和Log映射完成。给定 和切向量
和切向量  ,指数映射
,指数映射
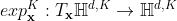
给点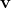 设置一个点
设置一个点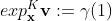 , 其 中
, 其 中  是唯一的满足
是唯一的满足 的测地线。
的测地线。
log映射是指数映射的逆,将点映射回切平面上的点
在一般的黎曼流形上,这两个算子只是局部定义的,而在双曲空间中,它们形成了双曲空间和某个点上切平面间的双射。我们如下定义指数映射和log映射以使得在双曲面流形的点上的操作可以映射到切空间中。
命题2:对于 ,
, ,
,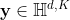 ,且
,且 , 指数和log映射定义为:
, 指数和log映射定义为:
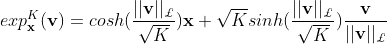
4 Hyperbbolic Graph Convolutional Networks(HGCN)
下面介绍HGCN,普通的GCN在双曲几何上的映射,它能同时利用图神经网络和双曲嵌入的优点。首先,由于输入的也正都是欧式空间里的,首先要把这些特征映射到双曲空间,然后介绍了图卷积网络的两个部分:特征转换和特征聚合,最后介绍带有可训练的曲率的HGCN。
从欧式空间到双曲空间的特征映射:
通过指数映射将输入特征从欧式空间映射到双曲流形上, 令 表示输入的欧式特征,令
表示输入的欧式特征,令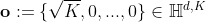 表示
表示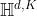 中的原点(在执行切空间操作时的参考点),我们有
中的原点(在执行切空间操作时的参考点),我们有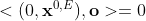 ,所以
,所以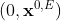 可看做切空间
可看做切空间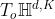 中的点,可以利用这个点结合命题2将欧式空间中的特征映射到双曲空间中去:
中的点,可以利用这个点结合命题2将欧式空间中的特征映射到双曲空间中去:
 (根据维度分开写的)
(根据维度分开写的)
双曲空间上的特征转换:
GCN中的特征转换用于将一个层中的嵌入空间映射到另一个层中,同时捕获邻居结果。现在我们要学习双曲面流形上点的转换。然而,在双曲空间中没有向量空间结构这一概念,这里在前人的工作之上定义出双曲面模型上的转换。主要思想是借助于指数映射和对数映射,这样就能在切空间上进行欧式变换。
双曲面线性变换:线性变换需要用一个权重矩阵取乘以嵌入向量,并加上一个偏置。为了计算权重矩阵乘法,首先利用对数映射将双曲空间中的点  映射到切空间
映射到切空间 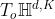 ,这样表示变换的矩阵就定义在切空间上,是欧几里得的,且与
,这样表示变换的矩阵就定义在切空间上,是欧几里得的,且与  同构,变换后再用指数映射将向量映射回双曲空间。令
同构,变换后再用指数映射将向量映射回双曲空间。令  表示
表示 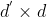 的权重矩阵,双曲矩阵乘法定义为:
的权重矩阵,双曲矩阵乘法定义为:

其中定义在
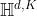 上,而
上,而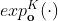 将向量映射到
将向量映射到上。
为了执行偏置加,还是利用前人的方法,定义切空间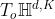 上的欧几里得向量
上的欧几里得向量 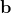 , 将其首先平行到流形上某一点的切平面上,然后再映射到流形上。如果
, 将其首先平行到流形上某一点的切平面上,然后再映射到流形上。如果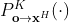 是从
是从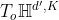 到
到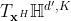 的平行移动,则双曲面偏置加定义为:
的平行移动,则双曲面偏置加定义为:

双曲面流形上的邻居聚合:
聚合在GCN中是非常关键的一步,因为它能捕获邻居结构和特征。假设 以权重
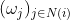 聚合其邻居信息
聚合其邻居信息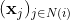 .均值聚合是计算加权和:
.均值聚合是计算加权和: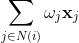 ,双曲空间上也有类似的加权和,但没有封闭的解。这里提出利用双曲注意力执行切空间上的聚合。
,双曲空间上也有类似的加权和,但没有封闭的解。这里提出利用双曲注意力执行切空间上的聚合。
注意力聚合:GCN中的注意力学习邻居的重要性并且根据它们的重要性将邻居信息聚合到中心点。但是,欧式空间中的注意力未考虑很多网路中存在的分层结构。这里提出基于双曲注意力的聚合。给定双曲嵌入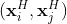 ,首先将
,首先将 和
和 映射到原点的切空间中,串联以后用多层感知机计算注意力。然后提出双曲聚合来平均节点的表示:
映射到原点的切空间中,串联以后用多层感知机计算注意力。然后提出双曲聚合来平均节点的表示:

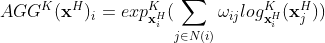
注意,这里是直接在每个点的切空间上进行的聚合,实验证明这样的聚合方式比在原点的切空间上聚合效果要好,因为相对距离失真更小。
不同曲率的非线性激活:类似于欧式聚合,HGCN利用非线性激活函数, 且满足
且满足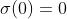 ,来学习非线性转换。给定l-1层和l层的双曲曲率
,来学习非线性转换。给定l-1层和l层的双曲曲率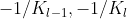 ,这里定义不同曲率的双曲非线性激活
,这里定义不同曲率的双曲非线性激活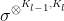 ,这一步非常重要因为它可以在每一层平滑地改变曲率。具体地,HGCN在切空间
,这一步非常重要因为它可以在每一层平滑地改变曲率。具体地,HGCN在切空间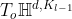 上进行欧式非线性激活,然后映射回
上进行欧式非线性激活,然后映射回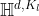 :
:

注意,为了应用指数映射,点必须位于原点的切空间上。幸运的是,同一维度不同曲率的双曲面流形的原点的切空间是同一个。所以上式是对的。
HGCN的架构:
介绍完HGCN所有的核心组件,现在总结其模型架构。给定一个图  和输入的欧式特征,HGCN的第一层将欧式特征映射到双曲空间中,然后堆叠几层图卷积,在每一层中在切空间上转换和聚合中心节点邻居的嵌入然后把结果映射到具有不同曲率的双曲空间中,在每一层中的信号传递过程为:
和输入的欧式特征,HGCN的第一层将欧式特征映射到双曲空间中,然后堆叠几层图卷积,在每一层中在切空间上转换和聚合中心节点邻居的嵌入然后把结果映射到具有不同曲率的双曲空间中,在每一层中的信号传递过程为:
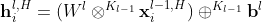 (双曲特征转换)
(双曲特征转换)
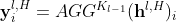 (基于注意力的邻居聚合)
(基于注意力的邻居聚合)
(不同曲率的非线性激活)
其中,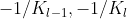 分别是l-1层和l层的双曲曲率。最后一层的双曲嵌入
分别是l-1层和l层的双曲曲率。最后一层的双曲嵌入用于下游任务。
对于连接预测任务,利用扩展的sigmoid取计算边的分数:
![p((i,j)\in E|\textbf{x}_{i}^{L,H},\textbf{x}_{j}^{L,H})=[e^{(d_{\pounds }^{K_{L}}(\textbf{x}_{i}^{L,H},\textbf{x}_{j}^{L,H})^2-r)/t}+1]^{-1}](https://i-blog.csdnimg.cn/blog_migrate/68a5d330c48d0821906559c7f8251c36.gif)
其中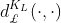 是双曲距离,
是双曲距离,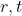 是超参数。通过最小化交叉熵来训练HGCN
是超参数。通过最小化交叉熵来训练HGCN
对于节点分类任务,首先用log映射将最后一层的输出映射到原点的切空间上,在切空间上进行欧式多项式逻辑回归。另一种可行的方式是直接在双曲流形上进行节点分类。最后,在节点分类任务上还加了一个连接预测正则化目标函数以鼓励最后一层的嵌入保持图结构。
























 1219
1219

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








