统计基础（八）二元数据

1.拟合模型到二元数据

二元数据格式为:{(xi, yi)}为i = 1,2，…， n.
x = (x1，…xn)T称为解释变量explabatory variable(或自变量independent variable、预测因子prdictor或回归因子regressor)，y = (y1，…(yn)>称为响应变量response variable(或因变量dependent variable)。这些由数据的上下文决定。
我们感兴趣的是拟合模型Yi= f (xi) + ∈i，∈i是误差,独立的函数f (x)。
我们只考虑简单线性模型: Y=β0 +β1 xi +∈。我注意到，指数模型和异速模型都可以通过对两边取对数来表示为简单的线性模型。

eg.
奥运会男子100米短跑比赛是田径运动中最负盛名的项目之一。卫冕冠军经常被称为“世界上跑得最快的人”，目前是牙买加人尤塞恩·博尔特。
每届奥运会的时间都在变快吗?你预计下一届奥运会的时间是什么时候?

1.1 构建散点图

第一步是构造一个y和x的散点图。这是二元数据的图形总结。
图中是否显示了y和x之间的线性关系?

1.2 拟合最小二乘回归线

如果散点图是线性的，那么我们拟合最小二乘的回归线。通过点，有许多可能的线，哪一条可以画在散点图上——但是哪一条是最佳的呢?

残差residuals
对于每个候选线f (x) =βˆ0 +βˆ1x，对于所有βˆ0和βˆ1,我们专注于合成的残差集:
∈ˆi(βˆ0, βˆ1) = yi- (βˆ0 + βˆ1xi)
这是直线和观测点之间的垂直距离。
例如，下面的图中，绿色残差为0.1581，紫色残差为0.22603。

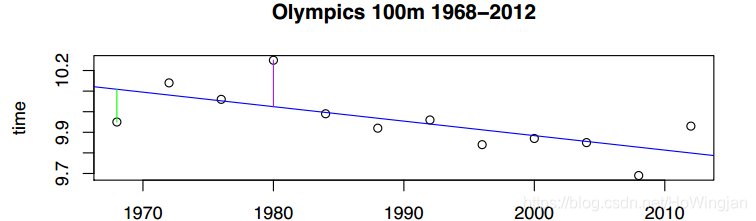
最小二乘法
可以使用lm()函数在R中拟合最小二乘回归线。

1.3 建模诊断

我们可以将一个模型与数据相匹配，但它是一个好的模型吗?
我们可以使用残差做出一些假设推理。
是否有一些定量的方法表明y和x之间有很强的线性关系?当数据点集合接近拟合直线时，即残差较小，则认为拟合良好。

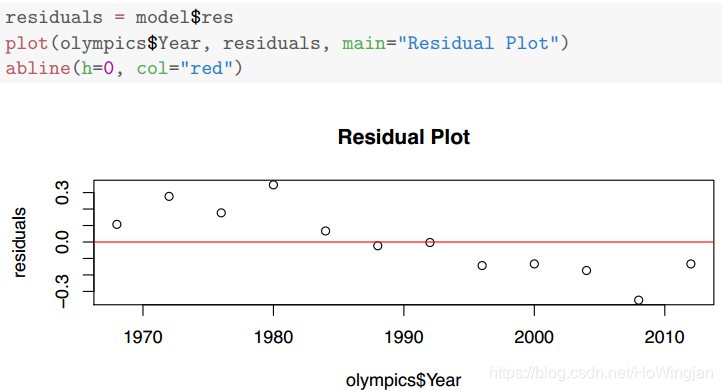
残差图
残差图是残差的散点图ˆ= y(βˆ0 +βˆ1 x)和x。
“图看起来是随机的，还是有规律可循?”
如果图是随机的，那么最小二乘拟合是好的。
如果图展示了一个关系ˆx,那么最小二乘行是不足够的,我们可能需要考虑更复杂的函数或转换(如y = x2或y =loga(x))。

皮尔逊样本相关系数
皮尔逊样本相关系数为：r=Sxy/sqrt(SxxSyy)
在本课程中，我们将简单地将其称为相关系数。
一些属性包括:r对x和y是对称的;1≤r≤1;r是数值总结，表示y和x之间的线性关联的强度;

r =±1为完美线性相关，所有数据点均位于最小二乘线上。
r = 0表示不存在线性相关，如斜率为零的直线，或随机散点，或非线性关系。

2.相关系数与斜率的关系

r和βˆ1有一个有趣的关系
r符号反映了数据的趋势(斜率)。
r不受尺度或原点变化的影响。

2.1决定系数

决定系数是模型中由x解释的y的可变性比例，或者在我们的语境中，由线性回归解释的可变性比例。
r^2≈1出现当ˆi = 0小s2y相比,即大部分的可变性与线性回归的模型。
r2 = 0时当s^2 = s2y,即没有一个模型的变化与线性回归相关联。
r2≈0时当s^2 ≈ s2y,即几乎没有变化的模型与线性回归相关联。
注意，r2可以很小，模型仍然是“有用的”，因为x和y之间可能有一个很低的关联。

2.2 相关性=/因果关系

相关性并不意味着因果关系。
r的高值并不一定意味着x和y之间存在因果关系。例如，12月份的温度和消费者支出。
同样，因果关系并不意味着高度相关

3.离群值outlier

离群值是由于大量数据分布不同而引起的观察结果。
即使一个异常值也会扭曲模型。

3.1Cook’s distance

使用Cook .distance(M1)可以找到线性模型对象M1的Cook 's distance®。
如果cook’s distance大于1，那么我们说相应的观测是一个异常值

3.2 leverage

通过使用lm.influence(M1)$h，您可以发现R中某个点对线性模型对象M1的影响。
如果leverage大于2p/n，其中p是回归次数
模型中的参数和n是观测的个数，那么我们说相应的观测具有很高的杠杆作用。在一个简单的线性回归中，我们有两个回归参数:截距和斜率，所以p = 2。

4.拟合一个简单的线性回归

考虑以下3个步骤:

1. 构造一个散点图:y vs x。
2. 如果图看起来线性的,符合最小平方(回归):y =βˆ0 +βˆ1 x。
3. 考虑一些模型诊断，例如
   • 检查残差图;
   • 相关系数或决定系数;
   • 检查是否有异常值使用库克的距离和杠杆价值。

4.1线性回归的推论

4.2 Q-Q图

分位数图或Q-Q图是一种图形方法，通过相互绘制它们的分位数来比较两个概率分布。
如果两个分布是相似的，Q-Q图中的点将近似地在直线y = x上。
如果这些点大致在直线y = a + bx上那么比较分布大约是N(a, b2)

4.3 多项式回归

如果线性趋势似乎不够充分(即使在转换之后)该怎么办?
对k阶多项式回归的拟合可以捕捉到一种趋势: