如何计算一个信号的信噪比

如何计算一个信号的信噪比

我都不知道什么是信号，什么噪声，该怎么估计信号分量和噪声分量呢？

信噪比（Signal-to-Noise Ratio, SNR）是衡量信号质量的一个重要指标。它表示信号功率与噪声功率的比值，通常以分贝（dB）为单位表示。信噪比越高，信号质量越好。

信号和噪声的定义

信号：在通信或数据处理中，信号是指有用的信息或数据。它可以是音频、视频、图像或其他形式的数据。

噪声：噪声是指干扰信号传输或处理的无用信息。它可以来自多种来源，如电子设备的热噪声、环境噪声等。

计算信噪比的步骤

测量信号功率：信号功率通常可以通过信号的均方值（RMS）来计算。对于一个离散信号 𝑥[𝑛]x[n]，信号功率 𝑃signalPsignal 可以表示为：

𝑃signal=1𝑁∑𝑛=0𝑁−1𝑥[𝑛]2Psignal=N1n=0∑N−1x[n]2

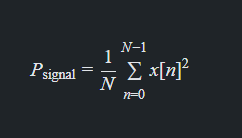
其中 𝑁N 是信号的样本数。

2. 测量噪声功率：噪声功率的计算方法与信号功率类似。通常需要先从总信号中分离出噪声分量，然后计算其均方值。

计算信噪比：信噪比 SNRSNR 可以通过信号功率与噪声功率的比值来计算：

SNR=𝑃signal𝑃noiseSNR=PnoisePsignal

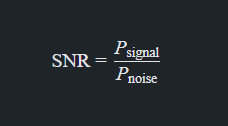
通常以分贝表示：

SNRdB=10⋅log⁡10(𝑃signal𝑃noise)SNRdB=10⋅log10(PnoisePsignal)

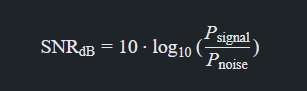
如何估计信号和噪声分量

信号分量：通常可以通过已知的信号模型或滤波方法来提取。例如，使用带通滤波器提取特定频率范围内的信号。

噪声分量：可以通过测量信号中不包含有用信息的部分来估计。例如，在音频信号中，静音段可以用来估计噪声。

示例代码

以下是一个简单的Python示例，演示如何计算信噪比：

import numpy as np

# 生成一个示例信号和噪声

np.random.seed(0)

signal = np.sin(2 * np.pi * 0.01 * np.arange(1000)) # 正弦信号

noise = np.random.normal(0, 0.5, 1000) # 高斯噪声

noisy_signal = signal + noise

# 计算信号和噪声的功率

signal_power = np.mean(signal**2)

noise_power = np.mean(noise**2)

# 计算信噪比

snr = signal_power / noise_power

snr_db = 10 * np.log10(snr)

print(f"SNR: {snr:.2f}")

print(f"SNR (dB): {snr_db:.2f} dB")

希望这能帮助你理解信噪比的计算过程！如果有其他问题，请随时问。

---

现在我手上只有一个一维信号，我该如何计算这个信号 的信噪比？

要计算一个一维信号的信噪比（SNR），你需要有信号和噪声的分量信息。如果你只有一个总信号而没有明确的信号和噪声分量，可以尝试以下方法：

方法1：假设噪声为零均值

如果你假设噪声是零均值的，可以通过以下步骤估计信噪比：

1. 估计信号功率：假设整个信号中有用信号占主导地位，计算整个信号的均方值作为信号功率。

估计噪声功率：如果你有信号的某些部分可以被认为是纯噪声（例如，静音段），可以用这些部分来估计噪声功率。

计算信噪比：使用信号功率和噪声功率计算信噪比。

方法2：使用滤波器分离信号和噪声

如果你对信号的频率特性有了解，可以使用滤波器来分离信号和噪声：

应用滤波器：使用带通滤波器提取信号的频率成分，使用带阻滤波器提取噪声。

计算功率：分别计算滤波后信号和噪声的功率。

计算信噪比：使用信号功率和噪声功率计算信噪比。

示例代码

以下是一个简单的Python示例，假设噪声为零均值，并使用整个信号的均方值作为信号功率：

import numpy as np

# 假设的信号

np.random.seed(0)

signal = np.sin(2 * np.pi * 0.01 * np.arange(1000)) # 正弦信号

noise = np.random.normal(0, 0.5, 1000) # 高斯噪声

noisy_signal = signal + noise

# 估计信号功率（假设整个信号为有用信号）

signal_power = np.mean(noisy_signal**2)

# 估计噪声功率（假设噪声为零均值）

noise_power = np.var(noise)

# 计算信噪比

snr = signal_power / noise_power

snr_db = 10 * np.log10(snr)

print(f"SNR: {snr:.2f}")

print(f"SNR (dB): {snr_db:.2f} dB")

请注意，这种方法的准确性依赖于对信号和噪声特性的假设。如果你能获得更多关于信号和噪声的信息，结果会更准确。

如何理解matlab中的snr函数，只有一个参数。如何估计出噪声的？

r = snr(sig); disp(['grid-cod without mask, SNR is ' num2str(r)]);

在 MATLAB 中，snr 函数可以用来计算信号的信噪比（SNR）。当你只传递一个参数（信号）给 snr 函数时，MATLAB 会自动估计噪声的功率。这是通过以下方式实现的：

MATLAB snr 函数的工作原理

信号功率：snr 函数首先计算输入信号的总功率。

噪声估计：当只有一个输入参数时，snr 函数假设信号中包含噪声，并通过信号的统计特性来估计噪声功率。具体来说，MATLAB 使用信号的自相关函数来估计噪声功率。自相关函数可以帮助分离信号的周期性成分和随机噪声。

信噪比计算：一旦信号和噪声的功率被估计出来，snr 函数就可以计算信噪比，并以分贝（dB）为单位返回结果。

使用示例

假设你有一个信号 sig，你可以使用 snr 函数来计算其信噪比：

% 生成一个示例信号

t = 0:0.001:1; % 时间向量

sig = sin(2pi10t) + 0.5randn(size(t)); % 正弦信号加上高斯噪声

% 计算信噪比

r = snr(sig);

% 显示结果

disp(['grid-cod without mask, SNR is ' num2str(r) ' dB']);

注意事项

假设：snr 函数在只有一个输入参数时，假设信号中包含噪声，并通过统计方法估计噪声功率。这种方法适用于信号中噪声成分相对较小且信号特性明确的情况。

准确性：如果你对信号和噪声有更多的了解（例如，知道噪声的特定特性或有纯噪声段），可以通过其他方法更准确地估计信噪比。

通过这种方式，MATLAB 的 snr 函数可以在没有明确噪声信息的情况下，提供一个信噪比的估计值。

为什么自相关函数可以来估计噪声功率?

自相关函数的定义

自相关函数是信号与其自身的延迟版本之间的相关性度量。对于一个离散信号 𝑥[𝑛]x[n]，其自相关函数 𝑅𝑥[𝑘]R**x[k] 定义为：

𝑅𝑥[𝑘]=∑𝑛𝑥[𝑛]⋅𝑥[𝑛+𝑘]R**x[k]=n∑x[n]⋅x[n+k]

其中 𝑘k 是延迟。

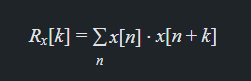
自相关函数与噪声

信号的周期性：对于周期性信号，自相关函数在其周期的整数倍处会有较大的值。这是因为信号的周期性成分在这些点上与自身高度相关。

2. 噪声的特性：噪声通常被假设为白噪声，即其自相关函数在非零延迟处的值接近于零。这是因为白噪声的样本之间没有相关性。

估计噪声功率

零延迟自相关：自相关函数在零延迟处的值 𝑅𝑥[0] 是信号的总功率，包括信号和噪声的功率。

非零延迟自相关：对于白噪声，自相关函数在非零延迟处的值接近于零。因此，信号的非零延迟自相关值主要反映信号的周期性成分。

通过分析自相关函数的形状和特性，可以分离出信号的周期性成分和噪声成分，从而估计噪声功率。

实际应用

在实际应用中，信号处理算法可能会使用自相关函数的统计特性来估计噪声功率。例如，信号的自相关函数在非零延迟处的平均值可以用作噪声功率的估计。

总结

自相关函数之所以能够用于噪声功率估计，是因为它能够揭示信号的周期性特性和噪声的随机特性。通过分析自相关函数的值，特别是在非零延迟处的值，可以有效地分离信号和噪声，从而估计噪声功率。