【漫话机器学习系列】273.高斯朴素贝叶斯分类器(Gaussian Naive Bayes Classifier)

【机器学习】图解高斯朴素贝叶斯分类器：原理、公式与应用

在机器学习的世界中，朴素贝叶斯分类器是一种常用的概率模型，特别适合处理文本分类、垃圾邮件识别、情感分析等任务。其优点是实现简单、计算高效、解释性强。而在连续型特征的场景下，高斯朴素贝叶斯分类器（Gaussian Naive Bayes Classifier）则是首选。

本文将结合一张生动易懂的手绘图，深入讲解高斯朴素贝叶斯分类器的原理与推导。

---

一、什么是朴素贝叶斯分类器？

朴素贝叶斯分类器是一种基于贝叶斯定理（Bayes' Theorem）与特征条件独立假设的监督学习算法。核心思想是：

通过先验概率和条件概率，计算后验概率，并选择最大概率的类别作为预测结果。

其数学基础是下面这条公式：

---

二、图解公式含义

我们来看这张图：

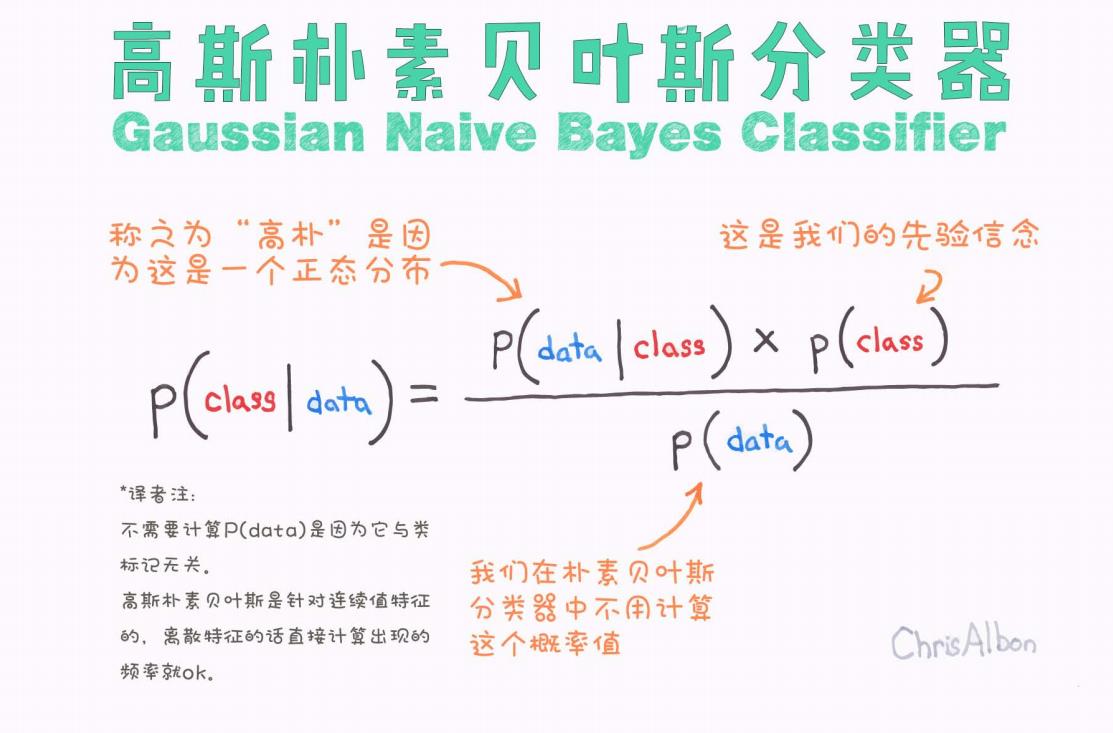
这张图用手写的方式非常直观地解释了贝叶斯公式中的每一部分：

• P(class | data)：后验概率。我们想要预测的目标，即在给定数据 data 的条件下属于某个 class 的概率。

• P(data | class)：似然。表示在该类别 class 下，观察到 data 的概率。

• P(class)：先验概率。是我们在没有看到 data 之前对每个类别的信念。

• P(data)：观测数据的边缘概率。在朴素贝叶斯中，这是一个归一化因子，不依赖类别，因此常常在比较大小时被忽略。

---

三、为什么叫“高斯”朴素贝叶斯？

图中也提到：“称之为‘高斯’是因为这是一个正态分布。”

这意味着对于每一个特征 ，我们假设它在每一个类别下是服从高斯分布（正态分布）的。其概率密度函数如下：

其中：

• μ 是该类别下该特征的均值

• 是该特征的方差

通俗理解：对于连续值特征，使用正态分布来估计每个类别中这些特征的出现概率。

---

四、为什么可以忽略 P(data)？

图中写道：

“我们在朴素贝叶斯分类器中不用计算这个概率值。”

这是因为我们最终是要找出哪个类别的 后验概率最大，而 P(data) 在所有类别下是相同的常数，不影响最终排序。换句话说：

---

五、朴素贝叶斯的“朴素”在哪里？

朴素贝叶斯的“朴素”，来源于它对特征之间的条件独立性假设，即：

在给定类别的情况下，所有特征之间相互独立。

虽然这个假设在现实中很少严格成立，但它在许多实际任务中仍然表现良好，尤其是特征之间冗余较少、噪声较小的任务场景。

---

六、高斯朴素贝叶斯的优缺点

优点：

• 训练速度快：只需要计算每个特征的均值和方差

• 对小数据集有效：不易过拟合

• 对高维数据效果好：如文本分类、基因数据分析

缺点：

• 特征独立假设过于强烈

• 对于特征不服从正态分布的数据效果较差

• 对异常值敏感

---

七、应用场景举例

• 垃圾邮件识别（Spam Classification）

• 情感分析（Sentiment Analysis）

• 医疗诊断预测

• 用户行为分类

• 文本主题识别

---

八、总结

通过这张图我们可以清晰地了解到：

• 高斯朴素贝叶斯的公式来源于贝叶斯定理

• 用高斯分布来模拟连续特征的似然性

• 分类时无需计算 P(data)，直接比较分子大小即可

尽管假设朴素，但这种方法却在现实中屡屡奏效，是你在机器学习中不可忽视的一种基础算法。

---

图源注：原图由 Chris Albon 绘制，本文为其内容的中文解析与整理。

如果你觉得本文有帮助，欢迎点赞、收藏、评论支持我继续更新更多机器学习原理图解系列！