梯度下降算法:
机器学习实现关键在于对参数的磨合,其中最关键的两个数:代价函数J(θ),代价函数对θ的求导∂J/∂θj。
如果知道这两个数,就能对参数进行磨合了: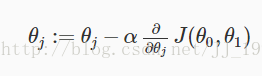
其中代价函数公式J(θ):
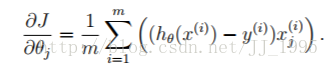
通过不断减低代价函数而得到准确的参数。
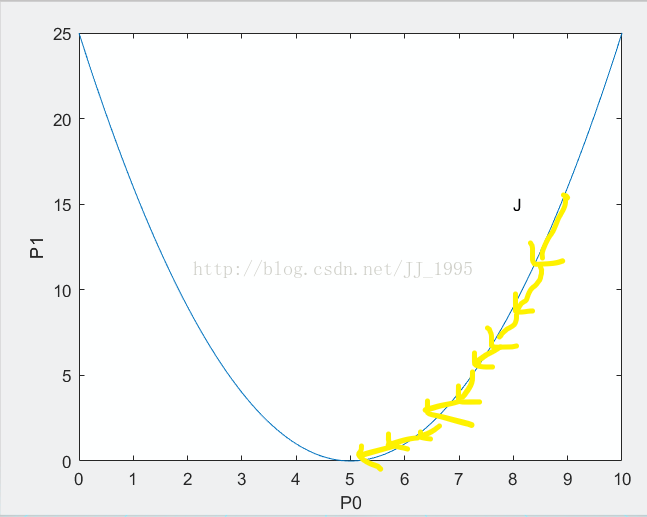
例如:
算法运行过程:给定初始参数p0,p1,通过算法一步一步调整P0,P1,使得J变小。
梯度下降算法适用范围:监督学习。
监督学习有两类问题:1.回归问题。2.分类问题。
1回归问题。
如房价预测。y = x1p1+x2p2+x3p3...;
计算代价函数时h(x) = x1p1+x2p2+x3p3...
2分类问题
如良性恶性肿瘤预测。y = sigmoid( x1p1+x2p2+x3p3....)有关;其中sigmoid(x) = 1/(1+ exp(-x))
cost J : = -log(h(x) ) if y = 1;
-log(1-h(x)) if y =0;
结合起来可得
MATLAB编码过程:
1.录入数据:
data = load('data.txt');
X = data(:, 1); y = data(:, 2);
X = [ones(m, 1), data(:,1)]; % Add a column of ones to x
2.计算代价函数cost funtion:
回归问题:J = sum((sum(theta' .* X,2) - y).^2)/(2*m);其中(sum(theta' .* X,2)为h(x)
分类问题:J = sum(-y.*log(sigmoid(sum((theta' .* X),2))) - (1-y).*log(1-sigmoid(sum((theta' .* X),2))))/m;
3.执行gradient Descent梯度下降算法:
预设参数theta,调整幅度alpha,调整次数iterations;
theta =gradientDescent(X, y, theta, alpha, iterations){
for iter = 1:num_iters
old_theta = theta;
theta(1)= theta(1) - alpha* sum((sum(old_theta' .* X,2) - y).*X(:,1))/m;
theta(2) = theta(2) - alpha* sum((sum(old_theta' .* X,2) - y).*X(:,2))/m;
end
}








 本文深入探讨了机器学习中的梯度下降算法,包括代价函数J(θ)和其导数∂J/∂θj的角色,以及如何通过调整参数来优化模型。介绍了在回归问题和分类问题中的应用,例如房价预测和良性恶性肿瘤预测,并提供了MATLAB代码示例进行代价函数计算和梯度下降算法的实现。
本文深入探讨了机器学习中的梯度下降算法,包括代价函数J(θ)和其导数∂J/∂θj的角色,以及如何通过调整参数来优化模型。介绍了在回归问题和分类问题中的应用,例如房价预测和良性恶性肿瘤预测,并提供了MATLAB代码示例进行代价函数计算和梯度下降算法的实现。
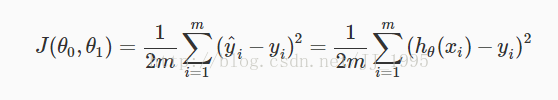
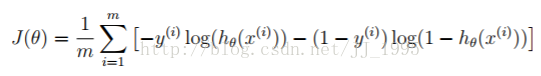














 742
742

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








